Class 10 : Maths (In English) – Lesson 5. Arithmetic Progressions

Posted by

On June 20, 2025

EXPLANATION & SUMMARY

✨ Explanation

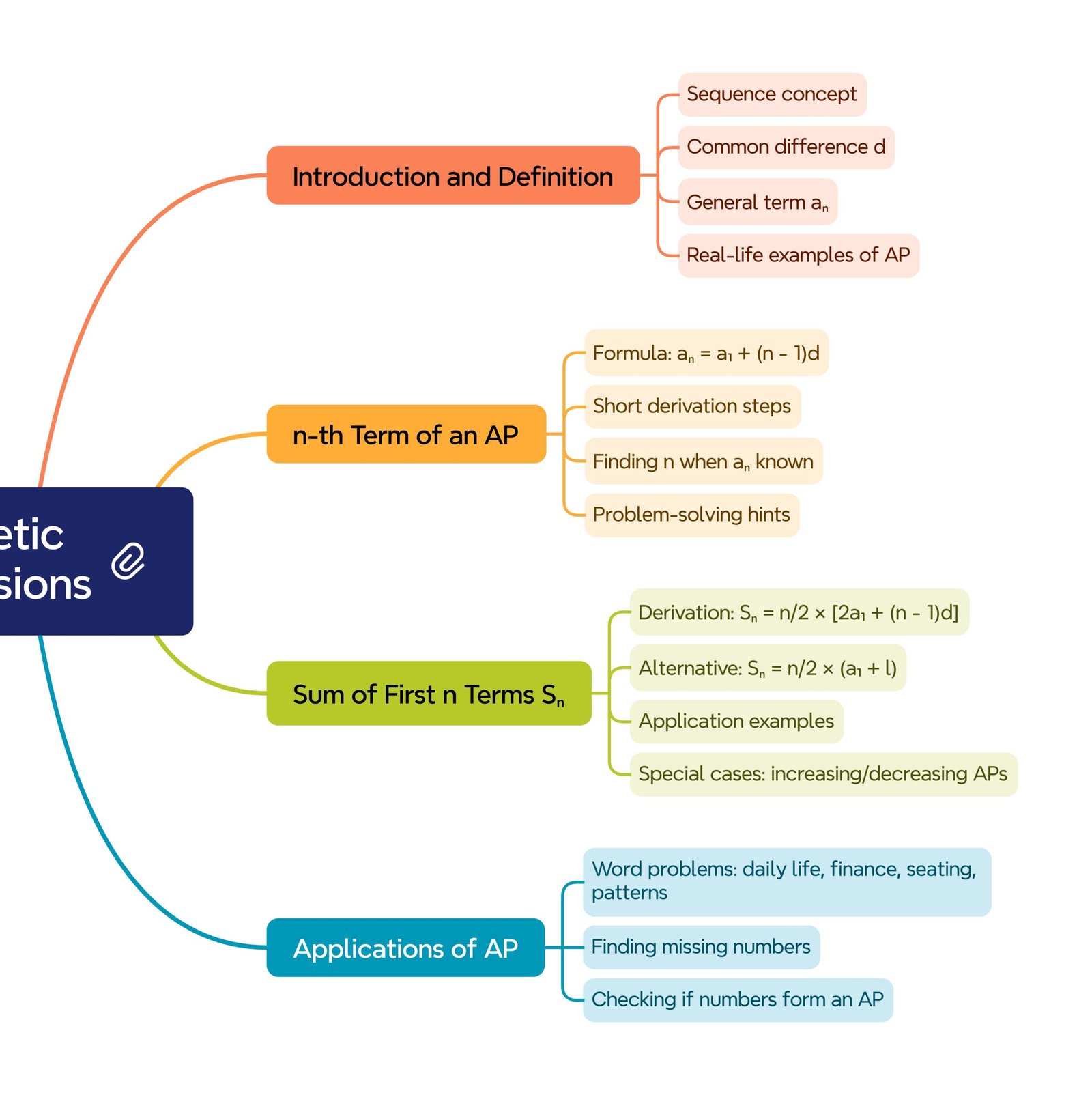
🔵 1) Sequences and Their Importance
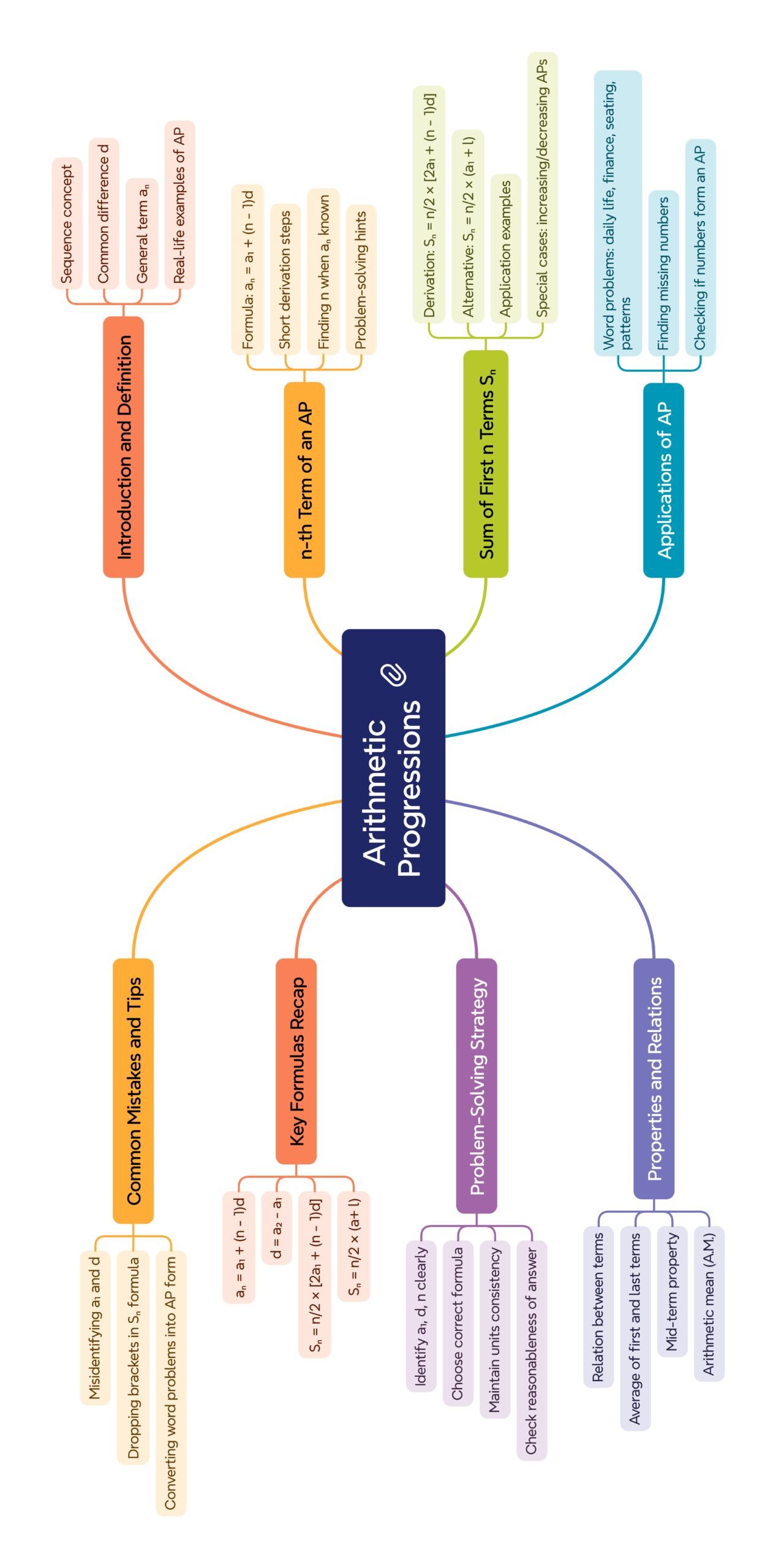
A sequence is an ordered list of numbers. Many real-life situations—bus fares increasing yearly, monthly savings rising by a fixed amount, or rows of seats with one extra chair each—show a constant change pattern. When each term differs by the same amount, the sequence is an Arithmetic Progression (AP).

🟢 2) Definition of Arithmetic Progression
➡️ A sequence a₁, a₂, a₃,… is an AP if
a₂ − a₁ = a₃ − a₂ = a₄ − a₃ = … = d,
where a (or a₁) is the first term and d is the common difference.

✔ Examples:

3, 7, 11, 15,… (d = 4)

100, 92, 84,… (d = −8)

5, 5, 5,… (d = 0)

✏ Note: Decimals or fractions can also form APs, e.g., 1.5, 1.7, 1.9,… (d = 0.2).

🔴 3) General Form & Visual Intuition
An AP can be written as:
a, a + d, a + 2d, a + 3d,…
Plotting term position n against value Tₙ gives a straight line, showing APs represent linear change.

💡 Concept: Think “add the same number each time.”

🟡 4) nth Term of an AP

Formula: Tₙ = a + (n − 1)d

🔵 Derivation

First term = a

Second term = a + d

Third term = a + 2d

Therefore Tₙ = a + (n − 1)d

Example: Find 10th term of 7, 13, 19,…
T₁₀ = 7 + 9×6 = 61

🟢 5) Checking If a Sequence Is an AP

Subtract consecutive terms. If the difference is constant, it’s an AP.
✔ Example: 2, 5, 8, 11 differences: 3, 3, 3 → AP
✏ Note: Check several differences to be sure.

🔵 6) Sum of First n Terms (Sₙ)

Two standard forms:
(i) Sₙ = n/2 (a + l)
(ii) Sₙ = n/2 [2a + (n − 1)d]

💡 Concept: Use whichever data—last term or d—is given.

Example: Sum of first 25 terms of 5, 9, 13,…
S₂₅ = 25/2 (10 + 96) = 25×53 = 1325

🔴 7) Finding Unknown Values

If T₅ = 18 and T₁₅ = 58:
a + 4d = 18
a + 14d = 58
Subtract → 10d = 40 ⇒ d = 4
a = 18 − 16 = 2

🟡 8) Inserting Arithmetic Means (A.M.s)

d = (B − A)/(m + 1)
Example: Insert 4 A.M.s between 3 and 23:
d = 20/5 = 4
Means: 7, 11, 15, 19

🟢 9) Applications of AP

🔵 Banking: Weekly savings increasing uniformly
🟢 Construction: Brick rows or tiles increasing by fixed numbers
🟡 Sports: Distances or repetitions increasing stepwise
🔴 Daily Life: Fare slabs or salary increments

✏ Note: Attach correct units (₹, m, cm) in word problems.

🔵 10) Determining Number of Terms

Use l = a + (n − 1)d.
Example: 64 = 4 + (n − 1)×5 ⇒ n = 13

🔴 11) Mixed Problems Using Tₙ and Sₙ

Example: T₂₀ = 99, d = 3 ⇒ a = 42
S₂₀ = 20/2 (84 + 57) = 1410

🟡 12) Graphical Insight

Plotting n vs Tₙ gives a line, linking AP to linear equations.

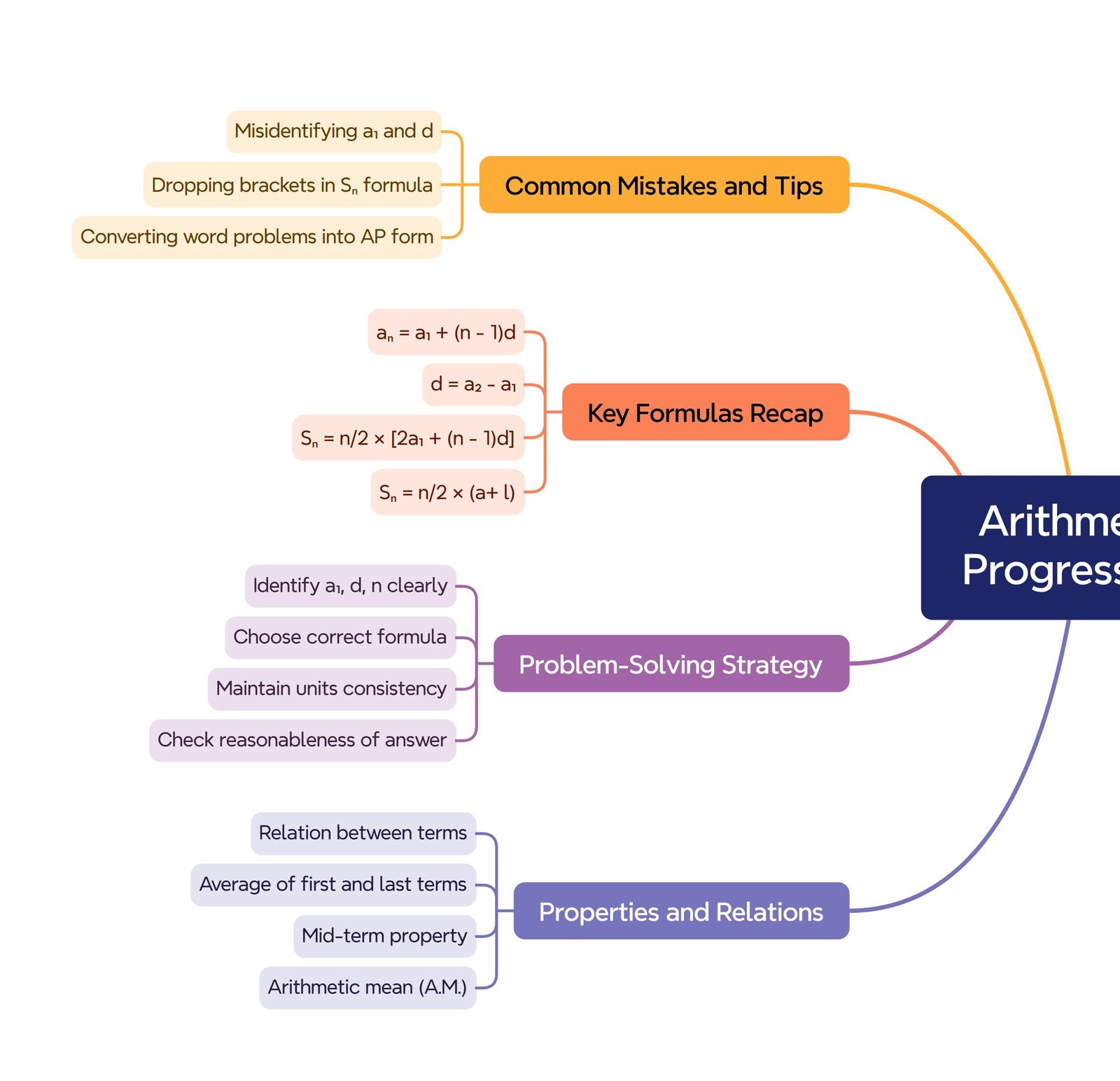
🧠 13) Common Mistakes

⚡ Forgetting (n − 1) in Tₙ
⚡ Sign errors with negative d
⚡ Mixing l and a
✔ Tip: List knowns first, then choose formula.

🌿 14) Higher Learning Connection

AP knowledge helps with geometric and harmonic progressions later.

⚡ 15) Real-Life Example

Staircase treads: a = 25 cm, d = 2 cm.
15th tread: 25 + 14×2 = 53 cm.
Total run: S₁₅ = 15/2 (50 + 28) = 585 cm.

📜 Summary (~300 words)

Definition & Recognition

AP: sequence with constant difference d

Form: a, a + d, a + 2d,…

Graph: straight line

Key Formulas

Tₙ = a + (n − 1)d

Sₙ = n/2 (a + l) = n/2 [2a + (n − 1)d]

l = a + (n − 1)d

Typical Problems

Find specific terms or sums

Insert A.M.s between two numbers

Determine n when l is known

Mixed word problems

Applications

Banking, construction, sports drills, salaries

Tips

Label knowns clearly

Check sign of d

Verify by substitution

Use exact values unless decimals are needed

📝 Quick Recap

🔵 AP = constant difference sequence

🟢 Tₙ = a + (n − 1)d; Sₙ = n/2 (a + l)

🟡 Insert means: d = (B − A)/(m + 1)

🔴 Graph is linear

✔ Always verify units and n-value

————————————————————————————————————————————————————————————————————————————

TEXTBOOK QUESTIONS

Exercise 5.1

🔵 Question 1
In which of the following situations, does the list of numbers involved make an arithmetic progression, and why?
(i) The taxi fare after each km when the fare is ₹ 15 for the first km and ₹ 8 for each additional km.
(ii) The amount of air present in a cylinder when a vacuum pump removes 1/4 of the air remaining in the cylinder at a time.
(iii) The cost of digging a well after every metre of digging, when it costs ₹ 150 for the first metre and rises by ₹ 50 for each subsequent metre.
(iv) The amount of money in the account every year, when ₹ 10000 is deposited at compound interest at 8 % per annum.

🟢 Answer
🔵 (i) Costs: 15, 23, 31,… (difference = 8) → AP ✔️
🔵 (ii) Air left: reduces by 1/4 each time (fractional ratio, not constant difference) → Not AP 🔴
🔵 (iii) Costs: 150, 200, 250,… (difference = 50) → AP ✔️
🔵 (iv) Compound interest grows multiplicatively (percentage), not by fixed addition → Not AP 🔴

🔵 Question 2
Write first four terms of the AP when the first term a and common difference d are:
(i) a = 10, d = 10 (ii) a = 2, d = 0 (iii) a = 4, d = –3 (iv) a = –1, d = ½ (v) a = –1.25, d = 0.25

🟢 Answer
🔵 (i) 10, 20, 30, 40
🔵 (ii) 2, 2, 2, 2
🔵 (iii) 4, 1, –2, –5
🔵 (iv) –1, –0.5, 0, 0.5
🔵 (v) –1.25, –1.00, –0.75, –0.50

🔵 Question 3
For the following APs, write the first term and the common difference:
(i) 3, 1, –1, –3,… (ii) –5, –1, 3, 7,… (iii) 1/3, 5/3, 9/3, 13/3,… (iv) 0.6, 1.7, 2.8, 3.9,…

🟢 Answer
🔵 (i) a = 3; d = 1 – 3 = –2 ✔️
🔵 (ii) a = –5; d = –1 – (–5) = 4 ✔️
🔵 (iii) a = 1/3; d = 5/3 – 1/3 = 4/3 ✔️
🔵 (iv) a = 0.6; d = 1.7 – 0.6 = 1.1 ✔️

🔵 Question 4
Which of the following are APs? If they form an AP, find the common difference d and write three more terms:
(i) 2, 4, 8, 16,… (ii) 2, 5/2, 3, 7/2,… (iii) –1.2, –3.2, –5.2, –7.2,… (iv) –10, –6, –2, 2,…
(v) 3, 3 + √2, 3 + 2√2, 3 + 3√2,… (vi) 0.2, 0.22, 0.222, 0.2222,… (vii) 0, –4, –8, –12,… (viii) –½, –1/2², –1/2³, –1/2⁴,…
(ix) 1, 3, 9, 27,… (x) a, 2a, 3a, 4a,… (xi) a, ar, ar², ar³,… (xii) √2, √8, √18, √32,…
(xiii) √3, √6, √9, √12,… (xiv) 1², 3², 5², 7²,… (xv) 1², 5², 7², 7³,…

🟢 Answer
🔵 (i) Differences 2, 4, 8 (not constant) → Not AP 🔴
🔵 (ii) Differences = 0.5 constant → AP; d = 0.5; next three terms: 4, 4.5, 5 ✔️
🔵 (iii) d = –2 constant → AP; next: –9.2, –11.2, –13.2 ✔️
🔵 (iv) d = 4 constant → AP; next: 6, 10, 14 ✔️
🔵 (v) d = √2 constant → AP; next: 3+4√2, 3+5√2, 3+6√2 ✔️
🔵 (vi) Differences: 0.02, 0.002,… (not constant) → Not AP 🔴
🔵 (vii) d = –4 constant → AP; next: –16, –20, –24 ✔️
🔵 (viii) Ratios, not constant differences → Not AP 🔴
🔵 (ix) Geometric (ratios), not AP → Not AP 🔴
🔵 (x) d = a constant → AP; next: 5a, 6a, 7a ✔️
🔵 (xi) Geometric, not AP → Not AP 🔴
🔵 (xii) Values: √2 ≈1.41, √8≈2.83, differences not constant → Not AP 🔴
🔵 (xiii) Values: √3≈1.73, √6≈2.45, differences vary → Not AP 🔴
🔵 (xiv) Squares of odd numbers: 1, 9, 25, 49,… differences vary (8,16,24) → Not AP 🔴
🔵 (xv) Values: 1, 25, 49,… differences vary → Not AP 🔴

Exercise 5.2

🔵 Question
Q1. Fill in the blanks in the following table, given that a is the first term, d the common difference and aₙ the nᵗʰ term of the AP:

🟢 Answer
💡 Concept: aₙ = a + (n − 1)d
(i) a = 7, d = 3, n = 8
🔵 Step 1: a₈ = 7 + (8 − 1)×3 = 7 + 21 = 28
✔️ Final: a₈ = 28

(ii) a = −18, n = 10, a₁₀ = 0
🔵 Step 1: 0 = −18 + (10 − 1)d ⇒ 9d = 18 ⇒ d = 2
✔️ Final: d = 2

(iii) d = −3, n = 18, a₁₈ = −5
🔵 Step 1: −5 = a + (18 − 1)(−3) = a − 51 ⇒ a = 46
✔️ Final: a = 46

(iv) a = −18.9, d = 2.5, aₙ = 3.6
🔵 Step 1: 3.6 = −18.9 + (n − 1)×2.5 ⇒ (n − 1)×2.5 = 22.5 ⇒ n − 1 = 9 ⇒ n = 10
✔️ Final: n = 10

(v) a = 3.5, d = 0, n = 105
🔵 Step 1: a₁₀₅ = 3.5 + (105 − 1)×0 = 3.5
✔️ Final: a₁₀₅ = 3.5

🔵 Question
Q2. Choose the correct choice in the following and justify:
(i) 30ᵗʰ term of the AP: 10, 7, 4, … , is (A) 97 (B) 77 (C) −77 (D) −87
(ii) 11ᵗʰ term of the AP: −3, −1/2, 2, … , is (A) 28 (B) 22 (C) −38 (D) −48 1/2

🟢 Answer
💡 Concept: Tₙ = a + (n − 1)d
(i)
🔵 Step 1: a = 10, d = 7 − 10 = −3
🔵 Step 2: T₃₀ = 10 + 29×(−3) = 10 − 87 = −77
✔️ Final: (C) −77

(ii)
🔵 Step 1: a = −3, d = (−1/2) − (−3) = 5/2
🔵 Step 2: T₁₁ = −3 + 10×(5/2) = −3 + 25 = 22
✔️ Final: (B) 22

🔵 Question
Q3. In the following APs, find the missing terms in the boxes:
(i) 2, [ ], [ ], 26
(ii) [ ], 13, [ ], 3
(iii) 5, [ ], [ ], 9 1/2
(iv) −4, [ ], [ ], [ ], 6
(v) 38, [ ], [ ], [ ], −22

🟢 Answer
💡 Concept: 4-term AP: d = (l − a)/3; 5-term AP: d = (l − a)/4
(i)
🔵 Step 1: d = (26 − 2)/3 = 8
🔵 Step 2: Terms = 2, 10, 18, 26
✔️ Final: 10, 18

(ii)
🔵 Step 1: Let d be common difference; 4ᵗʰ term = 13 + 2d = 3 ⇒ 2d = −10 ⇒ d = −5
🔵 Step 2: 1ˢᵗ term = 13 − d = 18; 3ʳᵈ term = 13 + d = 8
✔️ Final: 18, 8

(iii)
🔵 Step 1: l = 9.5; d = (9.5 − 5)/3 = 1.5
🔵 Step 2: Terms = 5, 6.5, 8, 9.5
✔️ Final: 6.5, 8

(iv)
🔵 Step 1: d = (6 − (−4))/4 = 2.5
🔵 Step 2: Terms = −4, −1.5, 1, 3.5, 6
✔️ Final: −1.5, 1, 3.5

(v)
🔵 Step 1: d = (−22 − 38)/4 = −15
🔵 Step 2: Terms = 38, 23, 8, −7, −22
✔️ Final: 23, 8, −7

🔵 Question
Q4. Which term of the AP: 3, 8, 13, 18, … is 78?

🟢 Answer
🔵 Step 1: a = 3, d = 5
🔵 Step 2: 3 + (n − 1)×5 = 78
🔵 Step 3: (n − 1)×5 = 75
🔵 Step 4: n − 1 = 15
🔵 Step 5: n = 16
✔️ Final: 16ᵗʰ term

🔵 Question
Q5. Find the number of terms in each of the following APs:
(i) 7, 13, 19, … , 205
(ii) 18, 15 1/2, 13, … , −47

🟢 Answer
(i)
🔵 Step 1: a = 7, d = 6, l = 205
🔵 Step 2: n = ((l − a)/d) + 1 = ((205 − 7)/6) + 1 = 33 + 1
🔵 Step 3: n = 34
✔️ Final: 34 terms

(ii)
🔵 Step 1: a = 18, d = 15.5 − 18 = −2.5, l = −47
🔵 Step 2: −47 = 18 + (n − 1)(−2.5)
🔵 Step 3: −65 = (n − 1)(−2.5)
🔵 Step 4: n − 1 = 26
🔵 Step 5: n = 27
✔️ Final: 27 terms

🔵 Question
Q6. Check whether −150 is a term of the AP: 11, 8, 5, 2, …

🟢 Answer
🔵 Step 1: a = 11, d = −3
🔵 Step 2: 11 + (n − 1)(−3) = −150
🔵 Step 3: 14 − 3n = −150
🔵 Step 4: −3n = −164
🔵 Step 5: n = 164/3 (not an integer)
✔️ Final: Not a term

🔵 Question
Q7. Find the 31ˢᵗ term of an AP whose 11ᵗʰ term is 38 and the 16ᵗʰ term is 73.

🟢 Answer
🔵 Step 1: a + 10d = 38
🔵 Step 2: a + 15d = 73
🔵 Step 3: Subtract ⇒ 5d = 35 ⇒ d = 7
🔵 Step 4: a = 38 − 10×7 = −32
🔵 Step 5: T₃₁ = a + 30d = −32 + 30×7 = 178
✔️ Final: T₃₁ = 178

🔵 Question
Q8. An AP consists of 50 terms of which 3ʳᵈ term is 12 and the last term is 106. Find the 29ᵗʰ term.

🟢 Answer
🔵 Step 1: a + 2d = 12
🔵 Step 2: a + 49d = 106
🔵 Step 3: Subtract ⇒ 47d = 94 ⇒ d = 2
🔵 Step 4: a = 12 − 2×2 = 8
🔵 Step 5: T₂₉ = a + 28d = 8 + 28×2 = 64
✔️ Final: T₂₉ = 64

🔵 Question
Q9. If the 3ʳᵈ and the 9ᵗʰ terms of an AP are 4 and −8 respectively, which term of this AP is zero?

🟢 Answer
🔵 Step 1: a + 2d = 4
🔵 Step 2: a + 8d = −8
🔵 Step 3: Subtract ⇒ 6d = −12 ⇒ d = −2
🔵 Step 4: a = 4 − 2d = 8
🔵 Step 5: 0 = a + (n − 1)d = 8 + (n − 1)(−2)
🔵 Step 6: 10 − 2n = 0 ⇒ n = 5
✔️ Final: 5ᵗʰ term

🔵 Question
Q10. The 17ᵗʰ term of an AP exceeds its 10ᵗʰ term by 7. Find the common difference.

🟢 Answer
🔵 Step 1: T₁₇ − T₁₀ = (a + 16d) − (a + 9d) = 7d
🔵 Step 2: 7d = 7 ⇒ d = 1
✔️ Final: d = 1

🔵 Question
Q11. Which term of the AP: 3, 15, 27, 39, …, will be 132 more than its 54ᵗʰ term?

🟢 Answer
🔵 Step 1: a = 3, d = 12
🔵 Step 2: T₅₄ = 3 + 53×12 = 639
🔵 Step 3: Required Tₙ = T₅₄ + 132 = 771
🔵 Step 4: 3 + (n − 1)×12 = 771 ⇒ (n − 1)×12 = 768 ⇒ n − 1 = 64 ⇒ n = 65
✔️ Final: 65ᵗʰ term

🔵 Question
Q12. Two APs have the same common difference. The difference between their 100ᵗʰ terms is 100. What is the difference between their 1000ᵗʰ terms?

🟢 Answer
💡 Concept: If d₁ = d₂, then Tₙ^(1) − Tₙ^(2) = a₁ − a₂ (independent of n)
🔵 Step 1: a₁ − a₂ = 100 (from 100ᵗʰ terms)
🔵 Step 2: Hence for n = 1000, difference = 100
✔️ Final: 100

🔵 Question
Q13. How many three-digit numbers are divisible by 7?

🟢 Answer
🔵 Step 1: First 3-digit multiple = 105; last = 994
🔵 Step 2: n = ((994 − 105)/7) + 1 = 127 + 1 = 128
✔️ Final: 128 numbers

🔵 Question
Q14. How many multiples of 4 lie between 10 and 250?

🟢 Answer
🔵 Step 1: First > 10 is 12; last < 250 is 248
🔵 Step 2: n = ((248 − 12)/4) + 1 = 59 + 1 = 60
✔️ Final: 60 multiples

🔵 Question
Q15. For what value of n, are the nᵗʰ terms of two APs: 63, 65, 67, … and 3, 10, 17, … equal?

🟢 Answer
🔵 Step 1: Tₙ^(1) = 63 + (n − 1)×2 = 61 + 2n
🔵 Step 2: Tₙ^(2) = 3 + (n − 1)×7 = 7n − 4
🔵 Step 3: 61 + 2n = 7n − 4 ⇒ 65 = 5n ⇒ n = 13
✔️ Final: n = 13

🔵 Question
Q16. Determine the AP whose 3ʳᵈ term is 16 and the 7ᵗʰ term exceeds the 5ᵗʰ term by 12.

🟢 Answer
🔵 Step 1: a + 2d = 16
🔵 Step 2: T₇ − T₅ = (a + 6d) − (a + 4d) = 2d = 12
🔵 Step 3: d = 6
🔵 Step 4: a = 16 − 2×6 = 4
✔️ Final: AP: 4, 10, 16, 22, … (a = 4, d = 6)

🔵 Question
Q17. Find the 20ᵗʰ term from the last term of the AP: 3, 8, 13, … , 253.

🟢 Answer
🔵 Step 1: a = 3, d = 5, l = 253
🔵 Step 2: n = ((l − a)/d) + 1 = 51
🔵 Step 3: 20ᵗʰ from last = T_{n − 20 + 1} = T₃₂
🔵 Step 4: T₃₂ = 3 + 31×5 = 158
✔️ Final: 158

🔵 Question
Q18. The sum of the 4ᵗʰ and 8ᵗʰ terms of an AP is 24 and the sum of the 6ᵗʰ and 10ᵗʰ terms is 44. Find the first three terms of the AP.

🟢 Answer
🔵 Step 1: (a + 3d) + (a + 7d) = 24 ⇒ 2a + 10d = 24 ⇒ a + 5d = 12 …(i)
🔵 Step 2: (a + 5d) + (a + 9d) = 44 ⇒ 2a + 14d = 44 ⇒ a + 7d = 22 …(ii)
🔵 Step 3: (ii) − (i) ⇒ 2d = 10 ⇒ d = 5
🔵 Step 4: From (i): a = 12 − 5×5 = −13
🔵 Step 5: First three terms = a, a + d, a + 2d = −13, −8, −3
✔️ Final: −13, −8, −3

🔵 Question
Q19. Subba Rao started work in 1995 at an annual salary of ₹5000 and received an increment of ₹200 each year. In which year did his income reach ₹7000?

🟢 Answer
🔵 Step 1: a = 5000 (1995), d = 200
🔵 Step 2: 7000 = 5000 + (n − 1)×200
🔵 Step 3: n − 1 = 10 ⇒ n = 11
🔵 Step 4: Year = 1995 + 10 = 2005
✔️ Final: 2005

🔵 Question
Q20. Ramkali saved ₹5 in the first week of a year and then increased her weekly savings by ₹1.75. If in the nᵗʰ week, her weekly savings become ₹20.75, find n.

🟢 Answer
🔵 Step 1: a = 5, d = 1.75
🔵 Step 2: 20.75 = 5 + (n − 1)×1.75
🔵 Step 3: n − 1 = 15.75/1.75 = 9
🔵 Step 4: n = 10
✔️ Final: 10ᵗʰ week

Exercise 5.3

🔵 Question
Q1. Find the sum of the following APs:
(i) 2, 7, 12, … , to 10 terms.
(ii) −37, −33, −29, … , to 12 terms.
(iii) 0.6, 1.7, 2.8, … , to 100 terms.
(iv) 1/15, 1/12, 1/10, … , to 11 terms.
🟢 Answer
✳️ (i)
💡 Concept: Sₙ = n/2 [2a + (n − 1)d]
🔵 Step 1: a = 2, d = 7 − 2 = 5, n = 10
🔵 Step 2: S₁₀ = 10/2 [2×2 + 9×5]
🔵 Step 3: S₁₀ = 5 [4 + 45]
🔵 Step 4: S₁₀ = 5 × 49
✔️ Final: S₁₀ = 245
✳️ (ii)
🔵 Step 1: a = −37, d = −33 − (−37) = 4, n = 12
🔵 Step 2: S₁₂ = 12/2 [2(−37) + 11×4]
🔵 Step 3: S₁₂ = 6 [−74 + 44]
🔵 Step 4: S₁₂ = 6 × (−30)
✔️ Final: S₁₂ = −180
✳️ (iii)
🔵 Step 1: a = 0.6, d = 1.7 − 0.6 = 1.1, n = 100
🔵 Step 2: S₁₀₀ = 100/2 [2×0.6 + 99×1.1]
🔵 Step 3: S₁₀₀ = 50 [1.2 + 108.9]
🔵 Step 4: S₁₀₀ = 50 × 110.1
✔️ Final: S₁₀₀ = 5505
✳️ (iv)
🔵 Step 1: a = 1/15, d = 1/12 − 1/15 = 1/60, n = 11
🔵 Step 2: S₁₁ = 11/2 [2(1/15) + 10(1/60)]
🔵 Step 3: S₁₁ = 11/2 [(2/15) + (10/60)]
🔵 Step 4: S₁₁ = 11/2 [(8/60) + (10/60)]
🔵 Step 5: S₁₁ = 11/2 × (18/60)
🔵 Step 6: S₁₁ = 11 × (3/20)
✔️ Final: S₁₁ = 33/20 = 1.65

🔵 Question
Q2. Find the sums given below:
(i) 7 + 10½ + 14 + … + 84
(ii) 34 + 32 + 30 + … + 10
(iii) −5 + (−8) + (−11) + … + (−230)
🟢 Answer
✳️ (i)
💡 Concept: Sₙ = n/2 (a + l)
🔵 Step 1: a = 7, d = 10.5 − 7 = 3.5, l = 84
🔵 Step 2: 84 = 7 + (n − 1)×3.5
🔵 Step 3: 77 = 3.5(n − 1) → n − 1 = 22 → n = 23
🔵 Step 4: S₂₃ = 23/2 (7 + 84)
🔵 Step 5: S₂₃ = 23/2 × 91
🔵 Step 6: S₂₃ = 23 × 45.5
✔️ Final: S₂₃ = 1046.5
✳️ (ii)
🔵 Step 1: a = 34, l = 10, d = 32 − 34 = −2
🔵 Step 2: 10 = 34 + (n − 1)(−2)
🔵 Step 3: −24 = −2(n − 1) → n − 1 = 12 → n = 13
🔵 Step 4: S₁₃ = 13/2 (34 + 10)
🔵 Step 5: S₁₃ = 13/2 × 44
🔵 Step 6: S₁₃ = 13 × 22
✔️ Final: S₁₃ = 286
✳️ (iii)
🔵 Step 1: a = −5, d = −8 − (−5) = −3, l = −230
🔵 Step 2: −230 = −5 + (n − 1)(−3)
🔵 Step 3: −225 = −3(n − 1) → n − 1 = 75 → n = 76
🔵 Step 4: S₇₆ = 76/2 (−5 + (−230))
🔵 Step 5: S₇₆ = 38 × (−235)
✔️ Final: S₇₆ = −8930

🔵 Question
Q3. In an AP:
(i) given a = 5, d = 3, aₙ = 50, find n and Sₙ.
(ii) given a = 7, a₁₃ = 35, find d and S₁₃.
(iii) given a₁₂ = 37, d = 3, find a and S₁₂.
(iv) given a₄ = 15, S₉ = 125, find a and a₂₀.
(v) given d = 5, S₉ = 75, find a and a₉.
(vi) given a = 2, d = 8, Sₙ = 90, find n and aₙ.
(vii) given a = 8, aₙ = 62, Sₙ = 210, find n and d.
(viii) given a = 4, d = 2, aₙ = −14, find n and aₙ (validity).
(ix) given a = 3, n = 8, Sₙ = 192, find d.
(x) given l = 28, Sₙ = 144 and there are total 9 terms. Find a.
🟢 Answer
✳️ (i)
🔵 Step 1: 50 = 5 + (n − 1)×3 → 45 = 3(n − 1)
🔵 Step 2: n − 1 = 15 → n = 16
🔵 Step 3: S₁₆ = 16/2 (5 + 50) = 8 × 55
✔️ Final: n = 16, S₁₆ = 440
✳️ (ii)
🔵 Step 1: a₁₃ = a + 12d = 35 → 7 + 12d = 35
🔵 Step 2: 12d = 28 → d = 7/3
🔵 Step 3: S₁₃ = 13/2 [2×7 + 12×(7/3)]
🔵 Step 4: S₁₃ = 13/2 (14 + 28) = 13/2 × 42
✔️ Final: d = 7/3, S₁₃ = 273
✳️ (iii)
🔵 Step 1: a = a₁₂ − 11d = 37 − 33 = 4
🔵 Step 2: S₁₂ = 12/2 [2×4 + 11×3]
🔵 Step 3: S₁₂ = 6 (8 + 33)
✔️ Final: a = 4, S₁₂ = 246
✳️ (iv)
🔵 Step 1: a + 3d = 15 …(1)
🔵 Step 2: S₉ = 9/2 [2a + 8d] = 125 → 9(a + 4d) = 125
🔵 Step 3: a + 4d = 125/9 …(2)
🔵 Step 4: (2) − (1): d = 125/9 − 15 = −10/9
🔵 Step 5: a = 15 − 3(−10/9) = 55/3
🔵 Step 6: a₂₀ = a + 19d = 55/3 + 19(−10/9) = −25/9
✔️ Final: a = 55/3, a₂₀ = −25/9
✳️ (v)
🔵 Step 1: S₉ = 9/2 [2a + 8×5] = 75
🔵 Step 2: 9(2a + 40) = 150 → 2a + 40 = 50/3
🔵 Step 3: 2a = −70/3 → a = −35/3
🔵 Step 4: a₉ = a + 8d = −35/3 + 40 = 85/3
✔️ Final: a = −35/3, a₉ = 85/3
✳️ (vi)
🔵 Step 1: 90 = Sₙ = n/2 [2×2 + (n − 1)×8]
🔵 Step 2: 90 = n/2 (8n − 4) = n(4n − 2)
🔵 Step 3: 4n² − 2n − 90 = 0 → 2n² − n − 45 = 0
🔵 Step 4: n = (1 ± 19)/4 → n = 5 (valid)
🔵 Step 5: aₙ = 2 + (5 − 1)×8 = 34
✔️ Final: n = 5, a₅ = 34
✳️ (vii)
🔵 Step 1: 210 = Sₙ = n/2 (a + aₙ) = n/2 (8 + 62)
🔵 Step 2: 210 = n/2 × 70 → 35n = 210 → n = 6
🔵 Step 3: d = (aₙ − a)/(n − 1) = (62 − 8)/5 = 54/5
✔️ Final: n = 6, d = 54/5
✳️ (viii)
🔵 Step 1: aₙ = a + (n − 1)d = 4 + (n − 1)×2
🔵 Step 2: 4 + 2n − 2 = 2n + 2
🔵 Step 3: For aₙ = −14 → 2n + 2 = −14 → n = −8 (invalid)
✔️ Final: No such positive n; aₙ = −14 is impossible for a = 4, d = 2
✳️ (ix)
🔵 Step 1: 192 = S₈ = 8/2 [2×3 + 7d]
🔵 Step 2: 192 = 4 (6 + 7d)
🔵 Step 3: 6 + 7d = 48 → 7d = 42 → d = 6
✔️ Final: d = 6
✳️ (x)
🔵 Step 1: n = 9, l = 28, S₉ = 144
🔵 Step 2: 144 = 9/2 (a + 28)
🔵 Step 3: 288 = 9(a + 28)
🔵 Step 4: a + 28 = 32 → a = 4
✔️ Final: a = 4

🔵 Question
Q4. How many terms of the AP: 9, 17, 25, … must be taken to give a sum of 636?
🟢 Answer
🔵 Step 1: a = 9, d = 8, Sₙ = 636
🔵 Step 2: 636 = n/2 [2×9 + (n − 1)×8]
🔵 Step 3: 636 = n/2 (8n + 10)
🔵 Step 4: 1272 = n(8n + 10)
🔵 Step 5: 8n² + 10n − 1272 = 0 → 4n² + 5n − 636 = 0
🔵 Step 6: Discriminant = 25 + 4×4×636 = 10201 = 101²
🔵 Step 7: n = (−5 + 101)/8 = 12
✔️ Final: n = 12

🔵 Question
Q5. The first term of an AP is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.
🟢 Answer
🔵 Step 1: Sₙ = 400, a = 5, l = 45
🔵 Step 2: n = 2Sₙ/(a + l) = 800/50 = 16
🔵 Step 3: d = (l − a)/(n − 1) = 40/15 = 8/3
✔️ Final: n = 16, d = 8/3

🔵 Question
Q6. The first and the last terms of an AP are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum?
🟢 Answer
🔵 Step 1: a = 17, l = 350, d = 9
🔵 Step 2: n = ((l − a)/d) + 1 = (333/9) + 1 = 38
🔵 Step 3: Sₙ = n/2 (a + l) = 38/2 × 367 = 19 × 367
✔️ Final: n = 38, S₃₈ = 6973

🔵 Question
Q7. Find the sum of first 22 terms of an AP in which d = 7 and 22ⁿᵈ term is 149.
🟢 Answer
🔵 Step 1: a + 21d = 149 → a = 149 − 147 = 2
🔵 Step 2: S₂₂ = 22/2 [2a + 21d]
🔵 Step 3: S₂₂ = 11 [4 + 147]
🔵 Step 4: S₂₂ = 11 × 151
✔️ Final: S₂₂ = 1661

🔵 Question
Q8. Find the sum of first 51 terms of an AP whose second and third terms are 14 and 18 respectively.
🟢 Answer
🔵 Step 1: a + d = 14, a + 2d = 18 → d = 4
🔵 Step 2: a = 14 − 4 = 10
🔵 Step 3: S₅₁ = 51/2 [2a + 50d]
🔵 Step 4: S₅₁ = 51/2 [20 + 200] = 51/2 × 220
🔵 Step 5: S₅₁ = 51 × 110
✔️ Final: S₅₁ = 5610

🔵 Question
Q9. If the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first n terms.
🟢 Answer
🔵 Step 1: S₇ = 7/2 [2a + 6d] = 49 → a + 3d = 7
🔵 Step 2: S₁₇ = 17/2 [2a + 16d] = 289 → a + 8d = 17
🔵 Step 3: Subtract → 5d = 10 → d = 2
🔵 Step 4: a = 7 − 3×2 = 1
🔵 Step 5: Sₙ = n/2 [2a + (n − 1)d] = n/2 [2 + 2(n − 1)]
🔵 Step 6: Sₙ = n/2 [2n] = n²
✔️ Final: Sₙ = n²

🔵 Question
Q10. Show that a₁, a₂, a₃, … form an AP where aₙ is defined as below. Also find the sum of the first 15 terms in each case:
(i) aₙ = 3 + 4n (ii) aₙ = 9 − 5n
🟢 Answer
✳️ (i)
🔵 Step 1: a₁ = 3 + 4×1 = 7
🔵 Step 2: a₂ − a₁ = (3 + 8) − 7 = 4 (constant) → AP
🔵 Step 3: a = 7, d = 4
🔵 Step 4: S₁₅ = 15/2 [2×7 + 14×4]
🔵 Step 5: S₁₅ = 15/2 (14 + 56) = 15/2 × 70
🔵 Step 6: S₁₅ = 15 × 35
✔️ Final: S₁₅ = 525
✳️ (ii)
🔵 Step 1: a₁ = 9 − 5×1 = 4
🔵 Step 2: a₂ − a₁ = (9 − 10) − 4 = −5 (constant) → AP
🔵 Step 3: a = 4, d = −5
🔵 Step 4: S₁₅ = 15/2 [2×4 + 14×(−5)]
🔵 Step 5: S₁₅ = 15/2 (8 − 70) = 15/2 × (−62)
🔵 Step 6: S₁₅ = 15 × (−31)
✔️ Final: S₁₅ = −465

🔵 Question
Q11. If the sum of the first n terms of an AP is Sₙ = 4n − n², what is the first term (that is S₁)? What is the sum of first two terms? What is the second term? Similarly, find the 3ʳᵈ, the 10ᵗʰ and the nᵗʰ terms.
🟢 Answer
💡 Concept: aₙ = Sₙ − S₍ₙ₋₁₎
🔵 Step 1: S₁ = 4(1) − 1² = 3
🔵 Step 2: S₂ = 4(2) − 2² = 8 − 4 = 4
🔵 Step 3: a₂ = S₂ − S₁ = 4 − 3 = 1
🔵 Step 4: S₍ₙ₋₁₎ = 4(n − 1) − (n − 1)²
🔵 Step 5: aₙ = (4n − n²) − [4(n − 1) − (n − 1)²]
🔵 Step 6: aₙ = 4n − n² − (4n − 4 − n² + 2n − 1)
🔵 Step 7: aₙ = 4n − n² − 4n + 4 + n² − 2n + 1 = 5 − 2n
🔵 Step 8: a₃ = 5 − 2(3) = −1
🔵 Step 9: a₁₀ = 5 − 2(10) = −15
✔️ Final: First term = 3; S₂ = 4; a₂ = 1; a₃ = −1; a₁₀ = −15; aₙ = 5 − 2n

🔵 Question
Q12. Find the sum of the first 40 positive integers divisible by 6.
🟢 Answer
➡️ Formula: Sₙ = n/2 (a + l)
🔵 Step 1: a = 6, l = 6×40 = 240, n = 40
🔵 Step 2: S₄₀ = 40/2 (6 + 240)
🔵 Step 3: S₄₀ = 20 × 246
✔️ Final: S₄₀ = 4920

🔵 Question
Q13. Find the sum of the first 15 multiples of 8.
🟢 Answer
➡️ Formula: Sₙ = n/2 (a + l)
🔵 Step 1: a = 8, l = 8×15 = 120, n = 15
🔵 Step 2: S₁₅ = 15/2 (8 + 120)
🔵 Step 3: S₁₅ = 15/2 × 128 = 15 × 64
✔️ Final: S₁₅ = 960

🔵 Question
Q14. Find the sum of the odd numbers between 0 and 50.
🟢 Answer
➡️ Formula: Sₙ = n/2 (a + l)
🔵 Step 1: Odd terms: 1, 3, …, 49 → a = 1, d = 2, l = 49
🔵 Step 2: n = ((l − a)/d) + 1 = ((49 − 1)/2) + 1 = 24 + 1 = 25
🔵 Step 3: S₂₅ = 25/2 (1 + 49)
🔵 Step 4: S₂₅ = 25/2 × 50 = 25 × 25
✔️ Final: 625

🔵 Question
Q15. A contractor job specifies a penalty for delay of completion beyond a certain date as follows: ₹200 for the first day, ₹250 for the second day, ₹300 for the third day, etc., the penalty for each succeeding day being ₹50 more than for the preceding day. How much money the contractor has to pay as penalty, if he has delayed the work by 30 days?
🟢 Answer
➡️ Formula: Sₙ = n/2 [2a + (n − 1)d]
🔵 Step 1: a = 200, d = 50, n = 30
🔵 Step 2: S₃₀ = 30/2 [2×200 + 29×50]
🔵 Step 3: S₃₀ = 15 [400 + 1450]
🔵 Step 4: S₃₀ = 15 × 1850
✔️ Final: ₹27750

🔵 Question
Q16. A sum of ₹700 is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is ₹20 less than its preceding prize, find the value of each of the prizes.
🟢 Answer
➡️ Formula: Sₙ = n/2 [2a + (n − 1)d] with d = −20, n = 7
🔵 Step 1: 700 = 7/2 [2a + 6(−20)]
🔵 Step 2: 700 = 7/2 (2a − 120)
🔵 Step 3: 700 = 7(a − 60) ⇒ a − 60 = 100 ⇒ a = 160
🔵 Step 4: Terms: 160, 140, 120, 100, 80, 60, 40
✔️ Final: Prizes = ₹160, ₹140, ₹120, ₹100, ₹80, ₹60, ₹40

🔵 Question
Q17. In a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees that each section of each class will plant will be the same as the class, in which they are studying, e.g., a section of Class I will plant 1 tree, a section of Class II will plant 2 trees and so on till Class XII. There are three sections of each class. How many trees will be planted by the students?
🟢 Answer
➡️ Sum needed: 3 × (1 + 2 + … + 12)
🔵 Step 1: n = 12, a = 1, l = 12
🔵 Step 2: Sum(1 to 12) = n/2 (a + l) = 12/2 (1 + 12) = 6 × 13 = 78
🔵 Step 3: Total trees = 3 × 78
✔️ Final: 234 trees

🔵 Question
Q18. A spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A, of radii 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm, … as shown in Fig. 5.4. What is the total length of such a spiral made up of thirteen consecutive semicircles? (Take π = 22/7.)
🟢 Answer
✏️ Note: Length of a semicircle of radius r is πr (arc only).
🔵 Step 1: Radii form an AP: a = 0.5, d = 0.5, n = 13
🔵 Step 2: Sum of radii = Sᵣ = n/2 [2a + (n − 1)d]
🔵 Step 3: Sᵣ = 13/2 [1.0 + 12×0.5] = 13/2 × 7 = 91/2
🔵 Step 4: Total length L = π × Sᵣ = (22/7) × (91/2)
🔵 Step 5: L = 22 × (13/2) = 11 × 13
✔️ Final: 143 cm

🔵 Question
Q19. 200 logs are stacked in the following manner: 20 logs in the bottom row, 19 in the next row, 18 in the row next to it and so on. In how many rows are the 200 logs placed and how many logs are in the top row?
🟢 Answer
➡️ Sum Sₙ = n/2 [2a + (n − 1)d], with a = 20, d = −1, Sₙ = 200
🔵 Step 1: 200 = n/2 [40 + (n − 1)(−1)]
🔵 Step 2: 200 = n/2 (41 − n)
🔵 Step 3: 400 = n(41 − n) ⇒ n² − 41n + 400 = 0
🔵 Step 4: Discriminant Δ = 41² − 4×400 = 1681 − 1600 = 81
🔵 Step 5: n = (41 ± 9)/2 ⇒ n = 16 (valid) or 25 (invalid as top row negative)
🔵 Step 6: Top row l = a + (n − 1)d = 20 + 15(−1) = 5
✔️ Final: 16 rows; top row has 5 logs

🔵 Question
Q20. In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato, and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line. A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket with it, and so on. She continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run?
[Hint: To pick up the first potato and second potato the total distance (in meters).]
🟢 Answer
💡 Concept: For each potato at distance dᵢ, distance run = 2dᵢ.
🔵 Step 1: Distances from start: 5, 8, 11, 14, … (a = 5, d = 3, n = 10)
🔵 Step 2: Sum of distances = S = n/2 [2a + (n − 1)d]
🔵 Step 3: S = 10/2 [10 + 9×3] = 5 [10 + 27] = 5 × 37 = 185
🔵 Step 4: Total running distance = 2S = 2 × 185
✔️ Final: 370 m

OTHER IMPORTANT QUESTIONS FOR EXAMS

🔵 Question
Q1. In the AP 5, 8, 11, … find the common difference.
🟢 Answer
➡ Formula: d = second − first
➡ Substitution: d = 8 − 5
✔ Final: d = 3

🔵 Question
Q2. State whether 42 is a term of the AP: 3, 7, 11, …
🟢 Answer
➡ Formula: Tₙ = a + (n − 1)d
➡ Substitution: 42 = 3 + (n − 1)×4 ⇒ (n − 1)×4 = 39 ⇒ n − 1 = 39/4 (not integer)
✔ Final: No, 42 is not a term.

🔵 Question
Q3. The 1ˢᵗ, 4ᵗʰ and 7ᵗʰ terms of an AP are p, q, r respectively. Find d.
🟢 Answer
➡ Relations: T₁ = a = p; T₄ = a + 3d = q
➡ Substitution: 3d = q − p ⇒ d = (q − p)/3
✔ Final: d = (q − p)/3

🔵 Question
Q4. The 10ᵗʰ term of an AP with a = 2 and d = 5 equals
🔵 (A) 45 🟢 (B) 47 🟡 (C) 52 🔴 (D) 55
🟢 Answer
➡ Formula: T₁₀ = a + 9d
➡ Substitution: T₁₀ = 2 + 9×5 = 47
✔ Final: (B) 47

🔵 Question
Q5. If Sₙ = n/2 [2a + (n − 1)d], then S₁ equals
🔵 (A) a 🟢 (B) 2a 🟡 (C) d 🔴 (D) a + d
🟢 Answer
➡ Substitution: S₁ = 1/2 [2a + 0] = a
✔ Final: (A) a

🔵 Question
Q6. In an AP, a = 12 and d = −3. Write T₄.
🟢 Answer
➡ Formula: T₄ = a + 3d
➡ Substitution: T₄ = 12 + 3(−3) = 3
✔ Final: T₄ = 3

🔵 Question
Q7. Find the 25ᵗʰ term of the AP 6, 9, 12, …
🟢 Answer
➡ Formula: Tₙ = a + (n − 1)d
➡ Substitution: T₂₅ = 6 + 24×3
➡ Simplification: T₂₅ = 6 + 72 = 78
✔ Final: T₂₅ = 78

🔵 Question
Q8. How many terms of the AP 4, 7, 10, … are needed to make a sum of 148?
🟢 Answer
➡ Formula: Sₙ = n/2 [2a + (n − 1)d]
➡ Substitution: 148 = n/2 [8 + (n − 1)×3]
➡ Simplification: 296 = n (3n + 5)
➡ Simplification: 3n² + 5n − 296 = 0 ⇒ n = 8
✔ Final: 8 terms

🔵 Question
Q9. If T₅ = 21 and T₁₁ = 45 for an AP, find a and d.
🟢 Answer
➡ Equations: a + 4d = 21; a + 10d = 45
➡ Subtraction: 6d = 24 ⇒ d = 4
➡ Back-substitution: a = 21 − 16 = 5
✔ Final: a = 5, d = 4

🔵 Question
Q10. The sum of n terms of an AP is Sₙ = 3n² − n. Find a and d.
🟢 Answer
➡ Concept: aₙ = Sₙ − S₍ₙ₋₁₎
➡ Substitution: aₙ = (3n² − n) − [3(n − 1)² − (n − 1)]
➡ Simplification: aₙ = 3n² − n − (3n² − 6n + 3 − n + 1) = 5n − 4
➡ a = a₁ = 5×1 − 4 = 1
➡ d = a₂ − a₁ = (10 − 4) − 1 = 5
✔ Final: a = 1, d = 5

🔵 Question
Q11. Insert three arithmetic means between −2 and 10.
🟢 Answer
➡ Formula: d = (B − A)/(m + 1)
➡ Substitution: d = (10 − (−2))/4 = 12/4 = 3
➡ Means: −2 + 3 = 1; −2 + 6 = 4; −2 + 9 = 7
✔ Final: 1, 4, 7

🔵 Question
Q12. The 15ᵗʰ term of an AP is 64 and its 5ᵗʰ term is 24. Find S₁₅.
🟢 Answer
➡ Equations: a + 14d = 64; a + 4d = 24
➡ Subtraction: 10d = 40 ⇒ d = 4
➡ Back-substitution: a = 24 − 16 = 8
➡ Formula: Sₙ = n/2 [2a + (n − 1)d]
➡ Substitution: S₁₅ = 15/2 [16 + 56] = 15/2 × 72
➡ Simplification: S₁₅ = 15 × 36
✔ Final: S₁₅ = 540

🔵 Question
Q13. Find the sum of the first 30 terms of the AP: 7, 10, 13,…
• Answer
➡ Formula: Sₙ = n/2 [2a + (n − 1)d]
➡ Substitution: S₃₀ = 30/2 [14 + 29×3]
➡ Simplification: S₃₀ = 15 [14 + 87] = 15×101
✔ Final: 1515

🔵 Question
Q14. The 19ᵗʰ term of an AP is 0. If the common difference is −3, find its first term and the sum of its first 19 terms.
• Answer
➡ Formula: T₁₉ = a + 18d
➡ Substitution: 0 = a + 18(−3) ⇒ a = 54
➡ S₁₉ = 19/2 (54 + 0) = 19×27
✔ Final: a = 54; S₁₉ = 513

🔵 Question
Q15. Find the number of terms in the AP: −6, −11, −16,… if its last term is −106. Also, find the sum.
• Answer
➡ Tₙ = a + (n−1)d = −6 + (n−1)(−5) = −106
➡ Simplification: −106 = −6 −5(n−1) ⇒ −100 = −5(n−1) ⇒ n−1 = 20 ⇒ n = 21
➡ S₂₁ = 21/2 (−6 + −106) = 21/2 (−112) = 21×(−56)
✔ Final: 21 terms; S₂₁ = −1176

🔵 Question
Q16. Show that 1, 5, 9,… forms an AP and find the 20ᵗʰ term.
• Answer
➡ Check d: 5−1=4; 9−5=4 (constant) ✔ AP
➡ Formula: T₂₀ = a + 19d = 1 + 19×4 = 77
✔ Final: T₂₀ = 77

🔵 Question
Q17. Find the sum of first 24 terms of the AP: –7, –4, –1,…
• Answer
➡ a = –7, d = 3
➡ S₂₄ = 24/2 [2(–7) + 23×3] = 12 [–14 + 69] = 12×55
✔ Final: 660

🔵 Question
Q18. The sum of 5 terms of an AP is –30 and its common difference is –3. Find the first term.
• Answer
➡ S₅ = 5/2 [2a + 4(–3)] = –30
➡ Simplification: 5/2 [2a – 12] = –30 ⇒ (5)(2a – 12) = –60 ⇒ 2a – 12 = –12
➡ 2a = 0 ⇒ a = 0
✔ Final: a = 0

🔵 Question
Q19. Which term of the AP: 15, 12.5, 10,… is –52.5?
• Answer
➡ a = 15, d = –2.5
➡ Tₙ = 15 + (n−1)(–2.5) = –52.5
➡ Simplification: –52.5 = 15 –2.5(n−1) ⇒ –67.5 = –2.5(n−1) ⇒ n−1 = 27 ⇒ n = 28
✔ Final: 28ᵗʰ term

🔵 Question
Q20. Find the sum of all odd numbers between 1 and 100.
• Answer
➡ Odd numbers: 1, 3,…, 99 → a=1, d=2, l=99
➡ n = ((99−1)/2)+1 = 50
➡ S₅₀ = 50/2 (1 + 99) = 25×100
✔ Final: 2500

🔵 Question
Q21. The sum of first seven terms of an AP is 49 and that of 17 terms is 289. Find the sum of first n terms.
• Answer
➡ S₇ = 7/2 [2a + 6d] = 49 ⇒ a + 3d = 7
➡ S₁₇ = 17/2 [2a + 16d] = 289 ⇒ a + 8d = 17
➡ Subtract: 5d = 10 ⇒ d = 2
➡ a = 7 – 3×2 = 1
➡ Sₙ = n/2 [2×1 + (n−1)×2] = n/2 [2 + 2n −2] = n/2 [2n] = n²
✔ Final: Sₙ = n²

🔵 Question
Q22. Internal Choice
(A) Find the 12ᵗʰ term of an AP whose 4ᵗʰ term is 18 and 8ᵗʰ term is 30.
OR
(B) The 9ᵗʰ term of an AP is 0 and the 29ᵗʰ term is –40. Find a and d.
• Answer (A)
➡ a + 3d = 18, a + 7d = 30 ⇒ 4d = 12 ⇒ d = 3
➡ a = 18 − 9 = 9
➡ T₁₂ = a + 11d = 9 + 33 = 42
✔ Final: 42
OR (B)
➡ a + 8d = 0, a + 28d = –40 ⇒ 20d = –40 ⇒ d = –2
➡ a = –8d = 16
✔ Final: a = 16, d = –2

Q23. The 7ᵗʰ term of an AP is 32 and the 13ᵗʰ term is 68. Find a, d and S₄₀.
Answer
➡ a + 6d = 32
➡ a + 12d = 68
➡ Subtract: 6d = 36 ⇒ d = 6
➡ a = 32 − 36 = −4
➡ S₄₀ = 40/2 [2a + (40 − 1)d] = 20[−8 + 234] = 20×226
✔ Final: a = −4, d = 6, S₄₀ = 4520

Q24. Find how many terms of 18, 15, 12,… give Sₙ = 180.
Answer
➡ a = 18, d = −3
➡ Sₙ = n/2 [2a + (n − 1)d] = n/2 (39 − 3n)
➡ 180 = n/2 (39 − 3n) ⇒ 360 = n(39 − 3n)
➡ 3n² − 39n + 360 = 0 → Δ = 1521 − 4320 = −2799 < 0
✔ Final: No natural n exists; sum 180 is impossible for this decreasing AP.

Q25. A) Sₙ = 2n² + 3n. Find a, d, a₂₀.
OR B) Sₙ = n(7n − 1)/2. Show a₉ − a₈ = 7.
Answer A
➡ aₙ = Sₙ − S₍ₙ₋₁₎
➡ S₍ₙ₋₁₎ = 2(n−1)² + 3(n−1) = 2n² − n − 1
➡ aₙ = (2n² + 3n) − (2n² − n − 1) = 4n + 1
➡ a = a₁ = 5; d = a₂ − a₁ = 9 − 5 = 4
➡ a₂₀ = 4×20 + 1 = 81
✔ Final: a = 5, d = 4, a₂₀ = 81
Answer B
➡ aₙ = Sₙ − S₍ₙ₋₁₎ = [n(7n − 1) − (n − 1)(7n − 8)]/2
➡ aₙ = (14n − 8)/2 = 7n − 4
➡ a₉ − a₈ = (63 − 4) − (56 − 4) = 63 − 56 = 7
✔ Final: a₉ − a₈ = 7

Q26. A) T₄ = 5, T₂₀ = 69. Find S₅₀.
OR B) S₂₀ = 710, S₄₀ = 3040. Find a and d.
Answer A
➡ a + 3d = 5; a + 19d = 69
➡ Subtract: 16d = 64 ⇒ d = 4
➡ a = 5 − 12 = −7
➡ S₅₀ = 50/2 [2a + 49d] = 25[−14 + 196] = 25×182
✔ Final: S₅₀ = 4550
Answer B
➡ S₂₀ = 10(2a + 19d) = 710 ⇒ 2a + 19d = 71
➡ S₄₀ = 20(2a + 39d) = 3040 ⇒ 2a + 39d = 152
➡ Subtract: 20d = 81 ⇒ d = 81/20 = 4.05
➡ 2a = 71 − 19×4.05 = −5.95 ⇒ a = −2.975
✔ Final: a = −2.975, d = 4.05

Q27. A) Three numbers in AP: first + third = 24, product = 135.
OR B) mᵗʰ term = 1/n, nᵗʰ term = 1/m. Show d = 1/(mn).
Answer A
➡ Numbers: a − d, a, a + d
➡ a − d + a + d = 24 ⇒ 2a = 24 ⇒ a = 12
➡ (12 − d)(12)(12 + d) = 135 ⇒ 12(144 − d²) = 135
➡ 144 − d² = 11.25 ⇒ d² = 132.75 = 531/4
➡ d = √531 / 2
✔ Final: 12 − √531/2, 12, 12 + √531/2
Answer B
➡ Tₘ = a + (m − 1)d = 1/n; Tₙ = a + (n − 1)d = 1/m
➡ (m − n)d = 1/n − 1/m = (m − n)/(mn)
➡ d = 1/(mn)
✔ Final: d = 1/(mn)

Q28. A farm has 25 rows: first row 12 trees, second 15, third 18,… Find total trees and last row.
Answer
➡ a = 12, d = 3, n = 25
➡ l = a + (n − 1)d = 12 + 24×3 = 84
➡ S₂₅ = 25/2 [2a + 24d] = 25/2 (24 + 72) = 25×48
✔ Final: Total = 1200, Last row = 84

Q29. If Tₚ = x and T_q = y, express T₍ₚ₊q₎, a and d.
Answer
➡ Tₚ = a + (p − 1)d = x
➡ T_q = a + (q − 1)d = y
➡ d = (y − x)/(q − p)
➡ a = x − (p − 1)(y − x)/(q − p)
➡ T₍ₚ₊q₎ = a + (p + q − 1)d = x + q(y − x)/(q − p)
✔ Final: T₍ₚ₊q₎ = x + q(y − x)/(q − p); d = (y − x)/(q − p); a = x − (p − 1)(y − x)/(q − p)

Q30. A ladder has 12 rungs. Lowest rung 25 cm from ground. First gap 20 cm, each next increases by Δ = 2 cm. Find height of 12ᵗʰ rung.
Answer
➡ Sum of first 11 gaps: S₁₁ = 11/2 [2×20 + (11 − 1)×2]
➡ S₁₁ = 11/2 (40 + 20) = 11/2×60 = 330 cm
➡ Total height = 25 + 330 = 355 cm
✔ Final: 355 cm