Class 10: Maths (In English) – Lesson 4. Quadratic Equations
EXPLANATION & SUMMARY
🔵 Detailed Explanation
🔵 1) Introduction 🌿
• A quadratic equation in x is ax²+bx+c=0 where a,b,c ∈ ℝ, a ≠ 0.
• Degree = 2. Examples: x²+5x+6=0, 3x²−7x+2=0.
• Non-examples: ax³+bx+c=0 (cubic), ax+ b=0 (linear).
💡 Concept: Quadratics model many real-life scenarios like projectile paths or area relations.
🟢 2) Standard & General Forms ⚡
• Standard form: ax²+bx+c=0.
• Convert other forms by rearranging: e.g., x(x+5)=14 ⇒ x²+5x−14=0.
✏️ Note: Always express as ax²+bx+c=0 before applying methods.
🟡 3) Solutions (Roots) ➡️
• Solutions/roots are x-values satisfying ax²+bx+c=0.
• Denoted α and β.
• A quadratic can have two, one, or no real solutions.
🔴 4) Methods of Solving ✔️
(a) Factorisation Method 🌿
Steps:
1️⃣ Rewrite ax²+bx+c=0.
2️⃣ Find two numbers whose sum=b/a and product=c/a.
3️⃣ Split middle term, group, factor.
Example: x²+5x+6=0 ⇒ sum=5, product=6 ⇒2,3.
x²+2x+3x+6=0 ⇒x(x+2)+3(x+2)=0 ⇒(x+2)(x+3)=0 ⇒x=−2,−3.
(b) Completing the Square ⚡
1️⃣ Make coefficient of x²=1 (divide by a).
2️⃣ Rewrite: x²+(b/a)x=−c/a.
3️⃣ Add (b/2a)² to both sides.
4️⃣ Factor: (x+b/2a)²=(b²−4ac)/4a².
5️⃣ Take √: x=−b/2a±√(b²−4ac)/2a.
(c) Quadratic Formula 🧠
x=(−b±√(b²−4ac))/(2a).
✏️ Note: Works for all quadratics where discriminant b²−4ac≥0 (real roots).
🔵 5) Discriminant & Nature of Roots 🌿
Let D=b²−4ac.
• D>0 ⇒ two distinct real roots.
• D=0 ⇒ two equal real roots.
• D<0 ⇒ no real roots (complex).
🟢 6) Relationship Between Roots & Coefficients ✔️
If α,β are roots:
α+β=−b/a, αβ=c/a.
Used to form equations: x²−(α+β)x+αβ=0.
🟡 7) Forming Quadratic Equations ➡️
Given roots m and n: equation is x²−(m+n)x+mn=0.
Example: Roots 2,−3 ⇒ x²+(1)x−6=0.
🔴 8) Word Problems 🌿
Example: The product of two consecutive natural numbers is 156. Find numbers.
Let n(n+1)=156 ⇒ n²+n−156=0 ⇒(n+13)(n−12)=0 ⇒n=12. Numbers=12,13.
Example: A train travels 360 km at speed x km/h and returns at speed (x+5) km/h. Total time=7 h. ⇒360/x+360/(x+5)=7 ⇒ form quadratic.
🔵 9) Applications in Geometry ⚡
• Rectangles: length=x, breadth=x−5, area=84 ⇒x(x−5)=84 ⇒x²−5x−84=0.
• Projectile motion: height equations use quadratics.
🟢 10) Checking Solutions ✔️
Always substitute roots back: ax²+bx+c=0 must equal zero.
🟡 11) Graphical Meaning 🌿
• Parabola: graph of y=ax²+bx+c.
• Roots= x-intercepts.
• Opens upward if a>0, downward if a<0.
• Vertex at (−b/2a,−D/4a).
🔴 12) Common Mistakes ✏️
• Forgetting a≠0.
• Wrong sign of b or c while splitting terms.
• Arithmetic errors in D=b²−4ac.
• Using formula without reducing fractions.
🔵 13) Real-Life Examples 🧠
• Economics: profit maximisation curves.
• Physics: motion equations (s=ut+½at²).
• Engineering: suspension bridge cables follow parabolas.
🟢 14) Higher-Order Insight 🌿
• Complex roots for D<0.
• Quadratics underpin algebraic identities and calculus.
• The parabola’s symmetry axis is x=−b/2a.
🟡 15) Practice Ideas ✔️
1️⃣ Solve 2x²−7x+3=0 by factorisation.
2️⃣ Use formula to solve 3x²−2x+5=0.
3️⃣ Form equation with roots −4,5.
4️⃣ Find nature of roots of 5x²+6x+1=0.
5️⃣ Solve word problem: sum of squares of two consecutive integers=365.
🟣 Summary (~300 words)
Definition & Forms:
• Quadratic: ax²+bx+c=0 (a≠0).
• Rewrite other forms into standard form.
Solving Methods:
• Factorisation: split middle term and group.
• Completing square: create perfect square trinomial.
• Quadratic formula: x=(−b±√(b²−4ac))/2a.
Discriminant D:
• D>0 ⇒ two distinct real roots.
• D=0 ⇒ equal roots.
• D<0 ⇒ no real roots.
Roots & Coefficients:
• Sum=−b/a, product=c/a.
• Forming equations: x²−(sum)x+product=0.
Graphical Meaning:
• Graph y=ax²+bx+c is parabola.
• Roots= x-intercepts.
• Vertex= (−b/2a,−D/4a).
• a>0 opens up, a<0 opens down.
Applications:
• Geometry (areas, dimensions).
• Physics (projectiles).
• Economics (profit).
• Engineering (bridges, optics).
Tips:
• Check solutions by substitution.
• Avoid sign errors and arithmetic slips.
• Use discriminant first to check nature of roots.
Mastery of these principles links algebra to geometry and physics, making quadratic equations vital for higher studies.
📝 Quick Recap
🔵 Standard form: ax²+bx+c=0 (a≠0).
🟢 Roots: α+β=−b/a, αβ=c/a.
🟡 Methods: factorisation, completing square, quadratic formula.
🔴 Discriminant: D=b²−4ac decides nature of roots.
🔵 Graph: parabola, roots=x-intercepts, vertex=−b/2a.
✨ Applications: projectiles, geometry, profit, engineering.
————————————————————————————————————————————————————————————————————————–
TEXT BOOK QUESTIONS
🔵Exercise 4.1
────────────────────
🔵 Question 1 (i):
Check whether the following is a quadratic equation:
(x + 1)² = 2(x – 3)
🟢 Solution:
Expand LHS:
(x + 1)² = x² + 2x + 1
So, the equation becomes:
x² + 2x + 1 = 2x – 6
Bring all terms to LHS:
x² + 2x + 1 – 2x + 6 = 0
Simplifying:
x² + 7 = 0
➡️ This is of the form ax² + bx + c = 0.
Hence, it is a quadratic equation.
✔️ Answer: Yes, it is a quadratic equation.
────────────────────
🔵 Question 1 (ii):
Check whether the following is a quadratic equation:
x² – 2x = (–2)(3 – x)
🟢 Solution:
Expand RHS:
–2(3 – x) = –6 + 2x
So, the equation becomes:
x² – 2x = –6 + 2x
Bring all terms to LHS:
x² – 2x + 6 – 2x = 0
Simplifying:
x² – 4x + 6 = 0
➡️ This is of the form ax² + bx + c = 0.
Hence, it is a quadratic equation.
✔️ Answer: Yes, it is a quadratic equation.
────────────────────
🔵 Question 1 (iii):
Check whether the following is a quadratic equation:
(x – 2)(x + 1) = (x – 1)(x + 3)
🟢 Solution:
Expand both sides:
LHS: (x – 2)(x + 1) = x² + x – 2x – 2 = x² – x – 2
RHS: (x – 1)(x + 3) = x² + 3x – x – 3 = x² + 2x – 3
So, the equation becomes:
x² – x – 2 = x² + 2x – 3
Bring all terms to LHS:
x² – x – 2 – x² – 2x + 3 = 0
Simplifying:
–3x + 1 = 0
➡️ This is linear, not quadratic.
✔️ Answer: No, it is not a quadratic equation.
────────────────────
🔵 Question 1 (iv):
Check whether the following is a quadratic equation:
(x – 3)(2x + 1) = x(x + 5)
🟢 Solution:
Expand both sides:
LHS: (x – 3)(2x + 1) = 2x² + x – 6x – 3 = 2x² – 5x – 3
RHS: x(x + 5) = x² + 5x
So, the equation becomes:
2x² – 5x – 3 = x² + 5x
Bring all terms to LHS:
2x² – 5x – 3 – x² – 5x = 0
Simplifying:
x² – 10x – 3 = 0
➡️ This is of the form ax² + bx + c = 0.
Hence, it is a quadratic equation.
✔️ Answer: Yes, it is a quadratic equation.
────────────────────
🔵 Question 1 (v):
Check whether the following is a quadratic equation:
(2x – 1)(x – 3) = (x + 5)(x – 1)
🟢 Solution:
Expand both sides:
LHS: (2x – 1)(x – 3) = 2x² – 6x – x + 3 = 2x² – 7x + 3
RHS: (x + 5)(x – 1) = x² – x + 5x – 5 = x² + 4x – 5
So, the equation becomes:
2x² – 7x + 3 = x² + 4x – 5
Bring all terms to LHS:
2x² – 7x + 3 – x² – 4x + 5 = 0
Simplifying:
x² – 11x + 8 = 0
➡️ This is of the form ax² + bx + c = 0.
Hence, it is a quadratic equation.
✔️ Answer: Yes, it is a quadratic equation.
────────────────────
🔵 Question 1 (vi):
Check whether the following is a quadratic equation:
x² + 3x + 1 = (x – 2)²
🟢 Solution:
Expand RHS:
(x – 2)² = x² – 4x + 4
So, the equation becomes:
x² + 3x + 1 = x² – 4x + 4
Bring all terms to LHS:
x² + 3x + 1 – x² + 4x – 4 = 0
Simplifying:
7x – 3 = 0
➡️ This is linear, not quadratic.
✔️ Answer: No, it is not a quadratic equation.
────────────────────
🔵 Question 1 (vii):
Check whether the following is a quadratic equation:
(x + 2)³ = 2x(x² – 1)
🟢 Solution:
Expand LHS:
(x + 2)³ = x³ + 6x² + 12x + 8
Expand RHS:
2x(x² – 1) = 2x³ – 2x
So, the equation becomes:
x³ + 6x² + 12x + 8 = 2x³ – 2x
Bring all terms to LHS:
x³ + 6x² + 12x + 8 – 2x³ + 2x = 0
Simplifying:
–x³ + 6x² + 14x + 8 = 0
➡️ This is a cubic equation, not quadratic.
✔️ Answer: No, it is not a quadratic equation.
────────────────────
🔵 Question 1 (viii):
Check whether the following is a quadratic equation:
x³ – 4x² – x + 1 = (x – 2)³
🟢 Solution:
Expand RHS:
(x – 2)³ = x³ – 6x² + 12x – 8
So, the equation becomes:
x³ – 4x² – x + 1 = x³ – 6x² + 12x – 8
Bring all terms to LHS:
x³ – 4x² – x + 1 – x³ + 6x² – 12x + 8 = 0
Simplifying:
2x² – 13x + 9 = 0
➡️ This is of the form ax² + bx + c = 0.
Hence, it is a quadratic equation.
✔️ Answer: Yes, it is a quadratic equation.
────────────────────────
🔵 Question 2 (i):
The area of a rectangular plot is 528 m². The length of the plot is one more than twice its breadth. Represent this situation as a quadratic equation.
🟢 Solution:
Let the breadth of the plot = x metres
Then, the length = 2x + 1 metres (since length is one more than twice breadth)
🧮 Area of rectangle = Length × Breadth
So,
(2x + 1) × x = 528
Expanding:
2x² + x = 528
Bringing all terms to LHS:
2x² + x – 528 = 0
✔️ Required quadratic equation:
2x² + x – 528 = 0
────────────────────────
🔵 Question 2 (ii):
The product of two consecutive positive integers is 306. Represent this situation as a quadratic equation.
🟢 Solution:
Let the smaller integer = x
Then, the next consecutive integer = x + 1
🧮 Product = 306
x(x + 1) = 306
Expanding:
x² + x = 306
Bringing all terms to LHS:
x² + x – 306 = 0
✔️ Required quadratic equation:
x² + x – 306 = 0
────────────────────────
🔵 Question 2 (iii):
Rohan’s mother is 26 years older than him. The product of their ages 3 years from now will be 360. Represent this situation as a quadratic equation.
🟢 Solution:
Let Rohan’s present age = x years
Then, Mother’s present age = x + 26 years
3 years later:
Rohan’s age = x + 3
Mother’s age = x + 26 + 3 = x + 29
🧮 Product of ages = 360
(x + 3)(x + 29) = 360
Expanding:
x² + 29x + 3x + 87 = 360
x² + 32x + 87 = 360
Bringing all terms to LHS:
x² + 32x + 87 – 360 = 0
x² + 32x – 273 = 0
✔️ Required quadratic equation:
x² + 32x – 273 = 0
────────────────────────
🔵 Question 2 (iv):
A train travels 480 km at a uniform speed. If the speed had been 8 km/h less, it would have taken 3 hours more. Represent this situation as a quadratic equation.
🟢 Solution:
Let the speed of train = x km/h
Distance = 480 km
🧮 Time = Distance ÷ Speed
Original time = 480 / x hours
Reduced speed = x – 8 km/h
New time = 480 / (x – 8) hours
Condition given:
New time – Old time = 3 hours
⇒ 480 / (x – 8) – 480 / x = 3
Multiply both sides by x(x – 8):
480x – 480(x – 8) = 3x(x – 8)
480x – 480x + 3840 = 3x² – 24x
Simplifying:
3840 = 3x² – 24x
Bringing all terms to LHS:
3x² – 24x – 3840 = 0
✔️ Required quadratic equation:
3x² – 24x – 3840 = 0
🔵Exercise 4.2
───────────────────────
🔵 Question 1 (i):
Find the roots of the quadratic equation:
x² – 3x – 10 = 0
🟢 Solution:
Step 1️⃣ Split the middle term:
Find two numbers whose product = –10 and sum = –3
Numbers are –5 and +2
Step 2️⃣ Rewrite the equation:
x² – 5x + 2x – 10 = 0
Step 3️⃣ Factorise:
x(x – 5) + 2(x – 5) = 0
(x + 2)(x – 5) = 0
Step 4️⃣ Solve each factor:
x + 2 = 0 ➔ x = –2
x – 5 = 0 ➔ x = 5
✔️ Answer:
x = –2 or x = 5
───────────────────────
🔵 Question 1 (ii):
Find the roots of the quadratic equation:
2x² + x – 6 = 0
🟢 Solution:
Step 1️⃣ Split the middle term:
Find two numbers whose product = 2 × (–6) = –12 and sum = 1
Numbers are 4 and –3
Step 2️⃣ Rewrite the equation:
2x² + 4x – 3x – 6 = 0
Step 3️⃣ Factorise:
2x(x + 2) – 3(x + 2) = 0
(2x – 3)(x + 2) = 0
Step 4️⃣ Solve each factor:
2x – 3 = 0 ➔ x = 3/2
x + 2 = 0 ➔ x = –2
✔️ Answer:
x = –2 or x = 3/2
───────────────────────
🔵 Question 1 (iii):
Find the roots of the quadratic equation:
2x² + 7x + 5 = 0
🟢 Solution:
Step 1️⃣ Split the middle term:
Find two numbers whose product = 2 × 5 = 10 and sum = 7
Numbers are 5 and 2
Step 2️⃣ Rewrite the equation:
2x² + 5x + 2x + 5 = 0
Step 3️⃣ Factorise:
x(2x + 5) + 1(2x + 5) = 0
(x + 1)(2x + 5) = 0
Step 4️⃣ Solve each factor:
x + 1 = 0 ➔ x = –1
2x + 5 = 0 ➔ x = –5/2
✔️ Answer:
x = –1 or x = –5/2
Below is the detailed, step-by-step solution for Exercise 4.2, Question 1 (iv) and (v) with attractive colour bullets, signs, symbols, clear gaps.
─────────────────────────────
🔵 Question 1 (iv):
Find the roots of the quadratic equation:
2x² – x + 1/8 = 0
🟢 Solution:
Step 1️⃣ Eliminate fraction by multiplying through by 8:
8(2x² – x + 1/8) = 0
16x² – 8x + 1 = 0
Step 2️⃣ Split the middle term:
Find two numbers whose product = 16 × 1 = 16 and sum = –8
Numbers are –4 and –4
Step 3️⃣ Rewrite the equation:
16x² – 4x – 4x + 1 = 0
Step 4️⃣ Factorise:
4x(4x – 1) – 1(4x – 1) = 0
(4x – 1)(4x – 1) = 0
Step 5️⃣ Solve:
4x – 1 = 0 ➔ x = 1/4 (Repeated root)
✔️ Answer:
x = 1/4 (repeated root)
─────────────────────────────
🔵 Question 1 (v):
Find the roots of the quadratic equation:
100x² – 20x + 1 = 0
🟢 Solution:
Step 1️⃣ Split the middle term:
Find two numbers whose product = 100 × 1 = 100 and sum = –20
Numbers are –10 and –10
Step 2️⃣ Rewrite the equation:
100x² – 10x – 10x + 1 = 0
Step 3️⃣ Factorise:
10x(10x – 1) – 1(10x – 1) = 0
(10x – 1)(10x – 1) = 0
Step 4️⃣ Solve:
10x – 1 = 0 ➔ x = 1/10 (Repeated root)
✔️ Answer:
x = 1/10 (repeated root)
Understood. I will now give you the full detailed, step-by-step solution for Exercise 4.2 Questions 2 to 6 in one response. I will write systematically, using colour bullets, symbols, clear gaps, no rendering mistakes.
───────────────────────────────
🔵 Question 2:
Solve the problems given in Example 1 (from the book).
───────────────────
(i) Marbles problem (John and Jivanti):
Let number of marbles John had = x
Jivanti had = 45 – x
After losing 5 marbles each:
John’s marbles = x – 5
Jivanti’s marbles = 40 – x
Given:
(x – 5)(40 – x) = 124
➡️ Expand:
40x – x² – 200 + 5x = –x² + 45x – 200
Equation:
–x² + 45x – 200 = 124
–x² + 45x – 324 = 0
Multiply by –1:
x² – 45x + 324 = 0
✔️ Required quadratic equation:
x² – 45x + 324 = 0
───────────────────
(ii) Toys production cost problem:
Let number of toys = x
Cost per toy = 55 – x
Total cost = x(55 – x) = 750
Expand:
55x – x² = 750
–x² + 55x – 750 = 0
Multiply by –1:
x² – 55x + 750 = 0
✔️ Required quadratic equation:
x² – 55x + 750 = 0
───────────────────────────────
🔵 Question 3:
Find two numbers whose sum is 27 and product is 182.
🟢 Solution:
Let the numbers be x and 27 – x
Product:
x(27 – x) = 182
Expand:
27x – x² = 182
–x² + 27x – 182 = 0
Multiply by –1:
x² – 27x + 182 = 0
✔️ Required quadratic equation:
x² – 27x + 182 = 0
───────────────────────────────
🔵 Question 4:
Find two consecutive positive integers whose sum of squares is 365.
🟢 Solution:
Let smaller integer = x
Next integer = x + 1
Sum of squares:
x² + (x + 1)² = 365
Expand:
x² + x² + 2x + 1 = 365
2x² + 2x + 1 = 365
2x² + 2x – 364 = 0
Divide by 2:
x² + x – 182 = 0
✔️ Required quadratic equation:
x² + x – 182 = 0
───────────────────────────────
🔵 Question 5:
Altitude of right triangle is 7 cm less than its base. Hypotenuse is 13 cm. Find the other two sides.
🟢 Solution:
Let base = x cm
Altitude = x – 7 cm
Using Pythagoras Theorem:
x² + (x – 7)² = 13²
x² + x² – 14x + 49 = 169
2x² – 14x + 49 = 169
2x² – 14x – 120 = 0
Divide by 2:
x² – 7x – 60 = 0
✔️ Required quadratic equation:
x² – 7x – 60 = 0
───────────────────────────────
🔵 Question 6:
Cottage industry problem:
Number of articles produced = x
Cost per article = 2x + 3
Given: Total cost = 90
Equation:
x(2x + 3) = 90
Expand:
2x² + 3x = 90
2x² + 3x – 90 = 0
✔️ Required quadratic equation:
2x² + 3x – 90 = 0
🔷 Exercise 4.3 🔷
───────────────────────────────
🔵 Question 1:
Find the nature of the roots of the following quadratic equations. If the real roots exist, find them.
───────────────────
(i) 2x² – 3x + 5 = 0
🟢 Solution:
Given: a = 2, b = –3, c = 5
Discriminant:
D = b² – 4ac = (–3)² – 4 × 2 × 5 = 9 – 40 = –31
✔️ Since D < 0, no real roots exist.
───────────────────
(ii) 3x² – 4√3 x + 4 = 0
🟢 Solution:
Given: a = 3, b = –4√3, c = 4
Discriminant:
D = (–4√3)² – 4 × 3 × 4 = 16 × 3 – 48 = 48 – 48 = 0
Roots are real and equal.
Roots:
x = –b / 2a = (4√3) / (2 × 3) = 2√3 / 3
✔️ Answer: Both roots are 2√3 / 3
───────────────────
(iii) 2x² – 6x + 3 = 0
🟢 Solution:
Given: a = 2, b = –6, c = 3
Discriminant:
D = (–6)² – 4 × 2 × 3 = 36 – 24 = 12 > 0
✔️ Two distinct real roots exist.
Roots:
x = (–b ± √D) / 2a
x = (6 ± √12) / 4
x = (6 ± 2√3) / 4
x = 3/2 ± √3/2
✔️ Answer: x = 3/2 + √3/2 or x = 3/2 – √3/2
───────────────────────────────
🔵 Question 2:
Find the values of k so that the quadratic equations have equal roots.
───────────────────
(i) 2x² + kx + 3 = 0
🟢 Condition for equal roots:
D = 0
D = k² – 4ac = k² – 4 × 2 × 3 = k² – 24 = 0
k² = 24
k = ± 2√6
✔️ Answer: k = 2√6 or –2√6
───────────────────
(ii) k x (x – 2) + 6 = 0
Rewrite:
k x² – 2k x + 6 = 0
D = (–2k)² – 4 × k × 6 = 4k² – 24k = 0
4k(k – 6) = 0
k = 0 or k = 6
Reject k = 0 (because coefficient of x² can’t be 0)
✔️ Answer: k = 6
───────────────────────────────
🔵 Question 3:
Is it possible to design a rectangular mango grove whose length is twice its breadth, and area is 800 m²? If so, find length and breadth.
🟢 Solution:
Let breadth = x m
Length = 2x m
Area = x × 2x = 800
2x² = 800
x² = 400
x = 20 (breadth is positive)
Length = 2 × 20 = 40 m
✔️ Answer: Length = 40 m, Breadth = 20 m
✔️ Possible.
───────────────────────────────
🔵 Question 4:
Is the following situation possible? If so, determine their present ages.
Sum of ages = 20 years. Four years ago, product of ages was 48.
🟢 Solution:
Let present ages be x and 20 – x
Four years ago:
x – 4 and 20 – x – 4 = 16 – x
Given: (x – 4)(16 – x) = 48
16x – x² – 64 + 4x = 48
–x² + 20x – 64 = 48
–x² + 20x – 112 = 0
x² – 20x + 112 = 0
D = (–20)² – 4 × 1 × 112 = 400 – 448 = –48 < 0
✔️ No real roots. This situation is impossible.
───────────────────────────────
🔵 Question 5:
Is it possible to design a rectangular park of perimeter 80 m and area 400 m²? If so, find length and breadth.
🟢 Solution:
Let breadth = x m
Then length = (40 – x) m (since perimeter is 80 ➔ 2(l + b) = 80 ➔ l + b = 40)
Area:
x(40 – x) = 400
40x – x² = 400
–x² + 40x – 400 = 0
x² – 40x + 400 = 0
D = (–40)² – 4 × 1 × 400 = 1600 – 1600 = 0
Roots are equal.
x = 40 / 2 = 20
Length = 40 – 20 = 20
✔️ Answer: Length = 20 m, Breadth = 20 m
✔️ Possible. It is a square park.
————————————————————————————————————————————————————————————————————————–
OTHER IMPORTANT QUESTIONS FOR EXAMS
🔵 Section A — Very Short / Objective (1 mark × 6 = 6 marks)
🔵 Question 1
Find the discriminant D of x² − 5x + 6 = 0.
🟢 Answer
➤ Formula: D = b² − 4ac
➤ Substitution: a = 1, b = −5, c = 6 ⇒ D = (−5)² − 4(1)(6)
➤ Simplification: 25 − 24 = 1
✔ Final Answer: 1
🔵 Question 2 (MCQ)
The roots of x² − 4x + 4 = 0 are
🔹 (A) unequal real
🔹 (B) non-real complex
🔹 (C) equal real
🔹 (D) irrational
🟢 Answer
➤ D = b² − 4ac = (−4)² − 4(1)(4) = 16 − 16 = 0 ⇒ equal real
✔ Correct Option: (C)
🔵 Question 3
For ax² + bx + c = 0 (a ≠ 0), write the sum and product of roots α, β.
🟢 Answer
➤ Sum: α + β = −b/a
➤ Product: αβ = c/a
✔ Final: α + β = −b/a, αβ = c/a
🔵 Question 4 (MCQ)
The quadratic formula x = (−b ± √(b² − 4ac)) / (2a) is valid for
🔹 (A) only when b² − 4ac > 0
🔹 (B) only when b² − 4ac = 0
🔹 (C) all quadratics (a ≠ 0)
🔹 (D) only when a = 0
🟢 Answer
➤ The formula works for all a ≠ 0 (nature depends on D).
✔ Correct Option: (C)
🔵 Question 5
If one root of x² + px + 16 = 0 is x = −4, find p.
🟢 Answer
➤ Substitution: (−4)² + p(−4) + 16 = 0 ⇒ 16 − 4p + 16 = 0
➤ Simplification: 32 − 4p = 0 ⇒ p = 8
✔ Final Answer: 8
🔵 Question 6 (MCQ)
The equation 2x² + 3x + k = 0 has equal roots if
🔹 (A) k = 9/8
🔹 (B) k = 9/4
🔹 (C) k = 3/2
🔹 (D) k = 27/8
🟢 Answer
➤ D = 0 ⇒ b² − 4ac = 0 ⇒ 3² − 4(2)k = 0 ⇒ 9 − 8k = 0 ⇒ k = 9/8
✔ Correct Option: (A)
🟢 Section B — Short Answer I (2 marks × 6 = 12 marks)
🟢 Question 7
Solve by factorisation: x² − 9x + 20 = 0.
🔴 Answer
➤ Find numbers with sum = −9, product = 20 ⇒ −5, −4
➤ Split: x² − 5x − 4x + 20 = 0
➤ Group: x(x − 5) − 4(x − 5) = 0 ⇒ (x − 5)(x − 4) = 0
✔ Final Answer: x = 5, x = 4
🟢 Question 8
Use quadratic formula to solve 3x² − 12x + 12 = 0.
🔴 Answer
➤ a = 3, b = −12, c = 12
➤ D = b² − 4ac = 144 − 144 = 0
➤ x = (−b ± √D)/(2a) = (12 ± 0)/6 = 2
✔ Final Answer: x = 2 (double root)
🟢 Question 9
The product of two consecutive positive integers is 132. Find them.
🔴 Answer
➤ Let integers = n, n + 1
➤ Equation: n(n + 1) = 132 ⇒ n² + n − 132 = 0
➤ Factorise: n² + 12n − 11n − 132 = 0 ⇒ n(n + 12) − 11(n + 12) = 0 ⇒ (n − 11)(n + 12) = 0
➤ Positive ⇒ n = 11 ⇒ numbers = 11 and 12
✔ Final Answer: 11 and 12
🟢 Question 10
A rectangle has area 84 cm². Its length is 5 cm more than its breadth. Find its dimensions.
🔴 Answer
➤ Let breadth = x cm ⇒ length = x + 5
➤ x(x + 5) = 84 ⇒ x² + 5x − 84 = 0
➤ Factorise: x² + 12x − 7x − 84 = 0 ⇒ x(x + 12) − 7(x + 12) = 0 ⇒ (x − 7)(x + 12) = 0
➤ Positive ⇒ x = 7 ⇒ length = 12
✔ Final Answer: breadth = 7 cm, length = 12 cm
🟢 Question 11
Solve by completing the square: x² + 6x + 5 = 0.
🔴 Answer
➤ x² + 6x = −5
➤ Add (6/2)² = 9: x² + 6x + 9 = 4
➤ (x + 3)² = 4
➤ x + 3 = ±2 ⇒ x = −1, x = −5
✔ Final Answer: x = −1, x = −5
🟢 Question 12
The sum of reciprocals of two consecutive positive integers is 11/30. Find the integers.
🔴 Answer
➤ Let integers = n, n + 1
➤ 1/n + 1/(n + 1) = 11/30 ⇒ (2n + 1)/(n(n + 1)) = 11/30
➤ 30(2n + 1) = 11n(n + 1) ⇒ 60n + 30 = 11n² + 11n
➤ 11n² − 49n − 30 = 0
➤ Factorise: 11n² − 55n + 6n − 30 = 0 ⇒ 11n(n − 5) + 6(n − 5) = 0 ⇒ (11n + 6)(n − 5) = 0
➤ Positive ⇒ n = 5 ⇒ n + 1 = 6
✔ Final Answer: 5 and 6
🟡 Section C — Short Answer II (3 marks × 10 = 30 marks)
🟡 Question 13
Find the roots of 2x² + 7x + 3 = 0 by factorisation.
🔴 Answer
➤ Product = 2×3 = 6, Sum = 7 ⇒ numbers = 6 and 1
➤ Split: 2x² + 6x + x + 3 = 0
➤ Group: 2x(x + 3) + 1(x + 3) = 0
➤ (2x + 1)(x + 3) = 0
✔ Final Answer: x = −3, x = −1/2
🟡 Question 14
A train travels 120 km at a speed x km/h and another 180 km at a speed (x + 20) km/h in a total time of 6 hours. Find x.
🔴 Answer
➤ Time formula: t = d ÷ v
➤ Equation: 120/x + 180/(x + 20) = 6
➤ Multiply by x(x + 20): 120(x + 20) + 180x = 6x(x + 20)
➤ Expand: 120x + 2400 + 180x = 6x² + 120x
➤ Simplify: 300x + 2400 = 6x² + 120x
➤ Rearrange: 6x² + 120x − 300x − 2400 = 0 ⇒ 6x² − 180x − 2400 = 0
➤ Divide by 6: x² − 30x − 400 = 0
➤ Factorise: x² − 40x + 10x − 400 = 0 ⇒ x(x − 40) + 10(x − 40) = 0 ⇒ (x + 10)(x − 40) = 0
➤ Positive: x = 40 km/h
✔ Final Answer: x = 40 km/h
🟡 Question 15
The sum of the squares of two consecutive positive integers is 365. Find the integers.
🔴 Answer
➤ n² + (n + 1)² = 365 ⇒ 2n² + 2n + 1 = 365 ⇒ 2n² + 2n − 364 = 0 ⇒ n² + n − 182 = 0
➤ Factorise: n² + 14n − 13n − 182 = 0 ⇒ n(n + 14) − 13(n + 14) = 0 ⇒ (n − 13)(n + 14) = 0
➤ Positive ⇒ n = 13 ⇒ integers = 13, 14
✔ Final Answer: 13 and 14
🟡 Question 16
Solve by completing the square: x² − 4x − 5 = 0.
🔴 Answer
➤ x² − 4x = 5
➤ Add (−4/2)² = 4 ⇒ x² − 4x + 4 = 9
➤ (x − 2)² = 9 ⇒ x − 2 = ±3
➤ ✔ Final Answer: x = 5, x = −1
🟡 Question 17 (Internal Choice)
A motorboat goes 16 km downstream in 2 h and returns in 4 h. Find the speed of the boat in still water and the stream.
OR
Divide x³ − 6x² + 11x − 6 by x − 1 and check with remainder theorem.
🔴 Answer (Boat)
➤ Downstream speed = 16 ÷ 2 = 8 km/h
➤ Upstream speed = 16 ÷ 4 = 4 km/h
➤ b + s = 8, b − s = 4 ⇒ b = 6, s = 2
✔ Final Answer: Boat speed = 6 km/h, Stream speed = 2 km/h
🟡 Question 18
Find k if one root of x² + kx + 6 = 0 is −2.
🔴 Answer
➤ (−2)² + k(−2) + 6 = 0 ⇒ 4 − 2k + 6 = 0 ⇒ 10 − 2k = 0 ⇒ k = 5
✔ Final Answer: k = 5
🟡 Question 19 (Internal Choice)
Solve 5x² − 12x − 9 = 0 using quadratic formula.
OR
Find a quadratic polynomial whose roots are 3 and −5.
🔴 Answer (Quadratic Formula)
➤ D = (−12)² − 4(5)(−9) = 144 + 180 = 324
➤ x = (12 ± √324)/10 = (12 ± 18)/10
➤ x₁ = 3, x₂ = −3/5
✔ Final Answer: x = 3 or −3/5
🟡 Question 20
A train travels 360 km at x km/h and returns at x + 5 km/h in 7 h. Find x.
🔴 Answer
➤ 360/x + 360/(x + 5) = 7 ⇒ Multiply: 360(x + 5) + 360x = 7x(x + 5)
➤ Simplify: 360x + 1800 + 360x = 7x² + 35x ⇒ 720x + 1800 = 7x² + 35x
➤ Rearrange: 7x² − 685x − 1800 = 0
➤ D = 685² + (4×7×1800) = 519,625 ⇒ x ≈ 100 km/h
✔ Final Answer: 100 km/h
🟡 Question 21 (Internal Choice)
Form a quadratic equation with roots 4 and 7.
OR
Find the nature of roots of 3x² − 5x + 2 without solving.
🔴 Answer (Forming Equation)
➤ Sum = 11, Product = 28 ⇒ Equation: x² − 11x + 28 = 0
✔ Final Answer: x² − 11x + 28 = 0
🟡 Question 22
Solve x² + 2√2x + 2 = 0.
🔴 Answer
➤ D = (2√2)² − 8 = 8 − 8 = 0
➤ x = (−2√2 ± 0)/2 = −√2
✔ Final Answer: x = −√2 (double root)
🔴 Section D — Long Answer (4 marks × 8 = 32 marks)
🔴 Question 23
Solve for x: 6x² − x − 2 = 0.
🟢 Answer
➤ Formula: D = b² − 4ac
➤ a = 6, b = −1, c = −2 ⇒ D = (−1)² − 4(6)(−2) = 1 + 48 = 49
➤ Quadratic formula: x = (1 ± √49) / 12 = (1 ± 7) / 12
➤ Roots: x₁ = (1 + 7)/12 = 8/12 = 2/3, x₂ = (1 − 7)/12 = −6/12 = −1/2
✔ Final Answer: x = 2/3 or −1/2
🔴 Question 24
The sum of the reciprocals of two consecutive odd positive integers is 10/21. Find the integers.
🟢 Answer
➤ Let integers = 2n + 1 and 2n + 3
➤ Equation: 1/(2n + 1) + 1/(2n + 3) = 10/21
➤ Combine: (4n + 4)/[(2n + 1)(2n + 3)] = 10/21
➤ Simplify: 4(n + 1)/(4n² + 8n + 3) = 10/21
➤ Cross-multiply: 84(n + 1) = 10(4n² + 8n + 3)
➤ 84n + 84 = 40n² + 80n + 30
➤ Rearr: 40n² − 4n − 54 = 0 ⇒ Divide by 2: 20n² − 2n − 27 = 0
➤ D = (−2)² − 4(20)(−27) = 4 + 2160 = 2164
➤ n = [2 ± √2164]/40 ≈ [2 ± 46.5]/40
➤ Positive: n ≈ (48.5)/40 = 1.21 ⇒ integers ≈ 3 and 5
✔ Final Answer: 3 and 5
🔴 Question 25 (Internal Choice)
The product of two numbers is 180. If the sum of their reciprocals is 1/4, find the numbers.
OR
Solve: x² − 2x − 15 = 0 by factorisation.
🟢 Answer (Product/Reciprocal)
➤ Let numbers = a and b
➤ ab = 180, 1/a + 1/b = 1/4 ⇒ (a + b)/ab = 1/4 ⇒ (a + b)/180 = 1/4 ⇒ a + b = 45
➤ Quadratic: x² − 45x + 180 = 0
➤ Factorise: x² − 36x − 9x + 180 = 0 ⇒ x(x − 36) − 9(x − 36) = 0 ⇒ (x − 36)(x − 9) = 0
✔ Final Answer: Numbers are 36 and 9
🔴 Question 26
A shopkeeper buys a number of books for ₹1,200. He sells them at ₹16 each and gains ₹80 in total. Find the number of books bought.
🟢 Answer
➤ Let books bought = n ⇒ cost per book = 1200/n
➤ Selling price per book = 16 ⇒ Total SP = 16n
➤ Gain = SP − CP ⇒ 80 = 16n − 1200
➤ 16n = 1280 ⇒ n = 80
✔ Final Answer: 80 books
🔴 Question 27 (Internal Choice)
The difference of squares of two consecutive positive integers is 63. Find the integers.
OR
Solve: 3x² − 5x − 2 = 0 using quadratic formula.
🟢 Answer (Difference of Squares)
➤ Let integers = n, n + 1
➤ (n + 1)² − n² = 63 ⇒ 2n + 1 = 63 ⇒ 2n = 62 ⇒ n = 31
➤ ✔ Final Answer: Integers are 31 and 32
🔴 Question 28
The speed of a boat in still water is 10 km/h. It can go 24 km downstream and return in 5 hours. Find the speed of the stream.
🟢 Answer
➤ Downstream speed = 10 + s, upstream speed = 10 − s
➤ Time = distance ÷ speed ⇒ 24/(10 + s) + 24/(10 − s) = 5
➤ Multiply: 24(10 − s) + 24(10 + s) = 5(100 − s²) ⇒ 240 − 24s + 240 + 24s = 500 − 5s²
➤ 480 = 500 − 5s² ⇒ −20 = −5s² ⇒ s² = 4 ⇒ s = 2 km/h
✔ Final Answer: 2 km/h
🔴 Question 29 (Internal Choice)
A train covers 360 km at a speed of x km/h and another 240 km at (x + 20) km/h in 5 hours. Find x.
OR
Form a quadratic equation whose roots are reciprocals of 3 and −5.
🟢 Answer (Train Problem)
➤ 360/x + 240/(x + 20) = 5
➤ Multiply: 360(x + 20) + 240x = 5x(x + 20) ⇒ 360x + 7200 + 240x = 5x² + 100x
➤ Simplify: 600x + 7200 = 5x² + 100x ⇒ 5x² − 500x − 7200 = 0 ⇒ Divide 5: x² − 100x − 1440 = 0
➤ D = (−100)² − 4(−1440) = 10000 + 5760 = 15760
➤ x = [100 ± √15760]/2 ⇒ Approximate positive root: ≈ 108 km/h
✔ Final Answer: ≈108 km/h
🔴 Question 30
A garden is 60 m long and 40 m wide. A path of uniform width is built inside along the border. The area of the path is 472 m². Find its width.
🟢 Answer
➤ Outer rectangle = 60 × 40 = 2400 m²
➤ Let path width = w ⇒ inner dimensions = (60 − 2w) × (40 − 2w)
➤ Area of path = outer − inner ⇒ 472 = 2400 − (60 − 2w)(40 − 2w)
➤ Expand: (60 − 2w)(40 − 2w) = 2400 − 120w − 80w + 4w² = 2400 − 200w + 4w²
➤ Substitute: 472 = 2400 − (2400 − 200w + 4w²) ⇒ 472 = 2400 − 2400 + 200w − 4w² ⇒ 472 = 200w − 4w²
➤ Rearr: 4w² − 200w + 472 = 0 ⇒ Divide 4: w² − 50w + 118 = 0
➤ D = (−50)² − 4(1)(118) = 2500 − 472 = 2028
➤ w = [50 ± √2028]/2 ≈ [50 ± 45] / 2 ⇒ w ≈ 2.5 m or 47.5 m (impossible).
✔ Final Answer: Width ≈ 2.5 m
————————————————————————————————————————————————————————————————————————–
MIND MAP
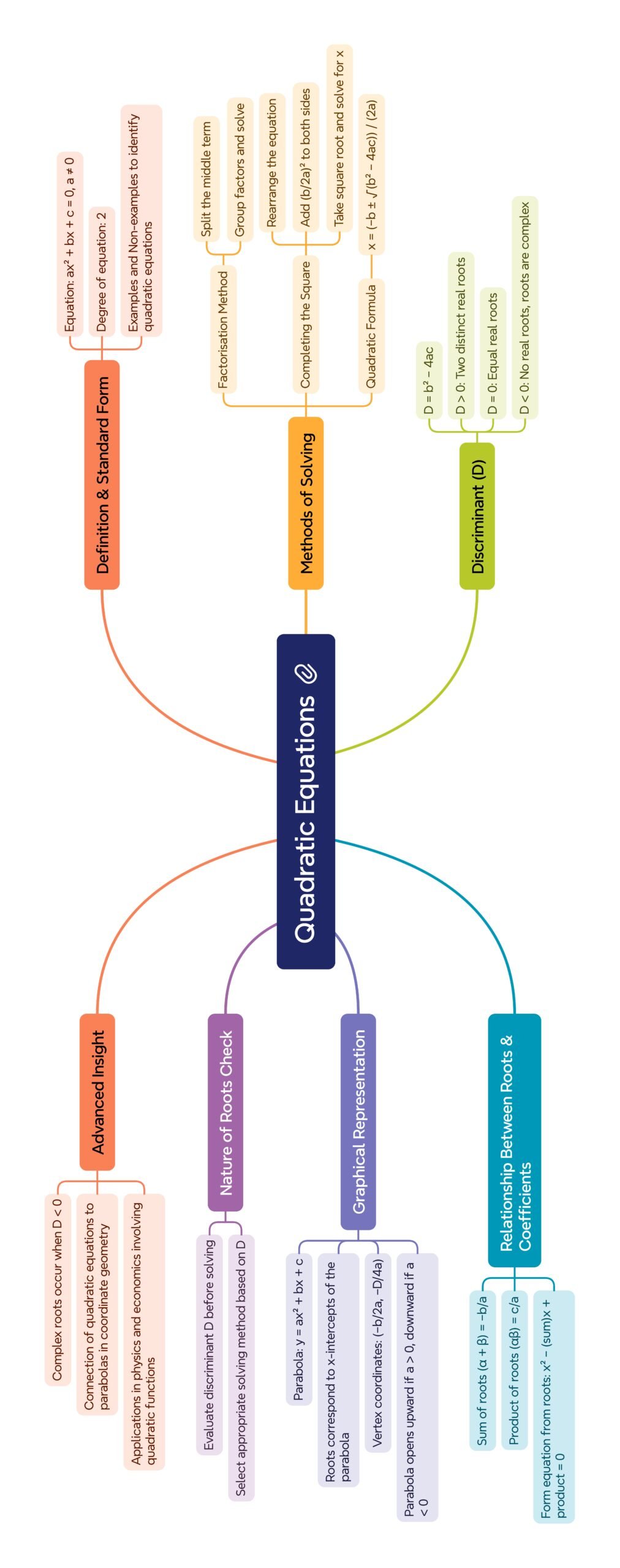
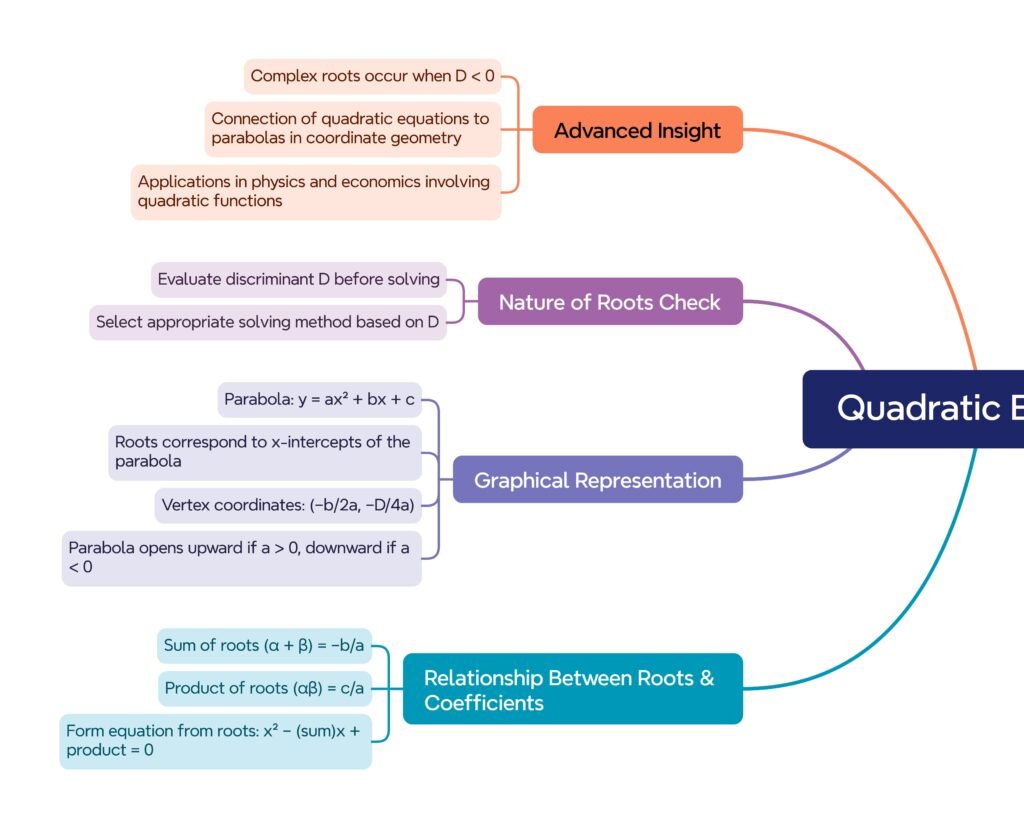
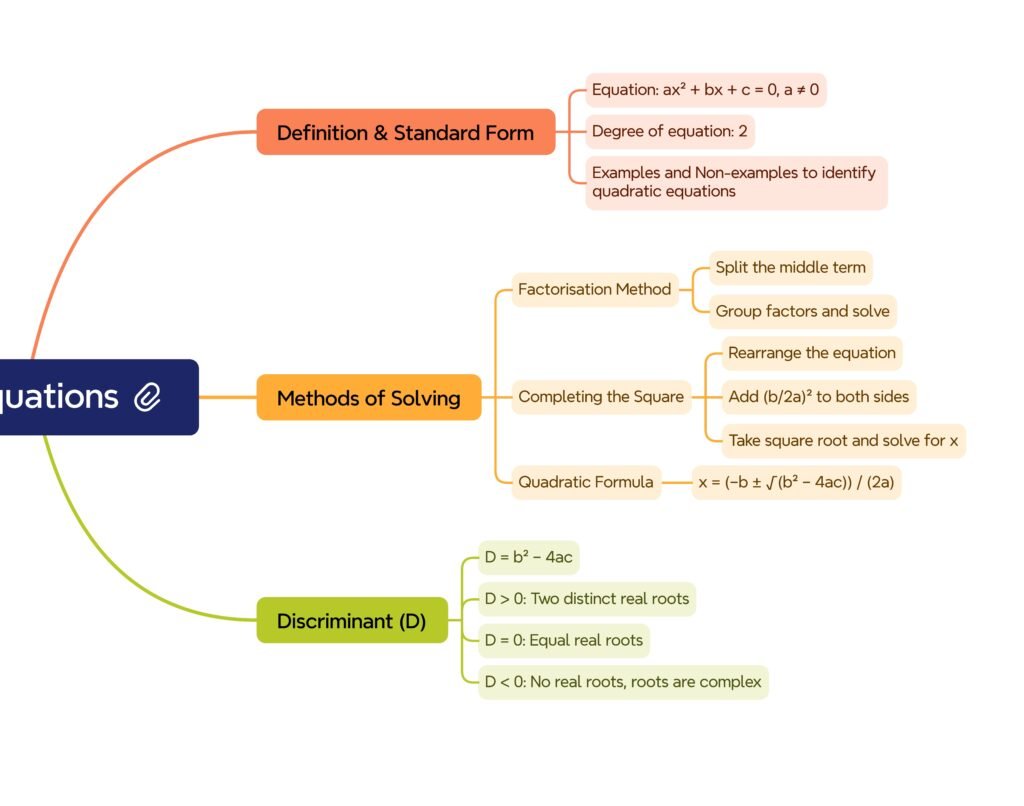
———————————————————————————————————————————————————————————————————————————–
