Class 10 : Maths (In English) – Lesson 3. Pair of Linear Equations in Two Variables
EXPLANATION & SUMMARY
🔵 Detailed Explanation
🔵 1) Introduction 🌿
• A linear equation in two variables has form ax+by+c=0 (a,b≠0 simultaneously).
• A pair of such equations is two relations in the same variables x and y:
a₁x + b₁y + c₁ = 0
a₂x + b₂y + c₂ = 0
• Solution = an ordered pair (x,y) satisfying both equations simultaneously.
• Real-life: Train ticket combinations, budget problems, mixture quantities—many require two linear conditions.
🟢 2) Graphical Interpretation ⚡
• Each equation represents a straight line in Cartesian plane.
• ✔ Intersections:
– Unique solution: Lines intersect at one point.
– Infinite solutions: Lines coincide.
– No solution: Lines parallel.
💡 Concept: Checking relative positions of two lines gives solution type.
🟡 3) Consistency & Types ➡️
• Ratios method:
Let equations be a₁x+b₁y+c₁=0 and a₂x+b₂y+c₂=0.
– If a₁/a₂ ≠ b₁/b₂ → Unique solution (intersecting).
– If a₁/a₂ = b₁/b₂ ≠ c₁/c₂ → No solution (parallel).
– If a₁/a₂ = b₁/b₂ = c₁/c₂ → Infinite solutions (coincident).
✏️ Note: Use simplified ratios to avoid mistakes.
🔴 4) Graphical Solution ✔️
Example: 2x+y=6 and x−y=1.
1️⃣ Rewrite: y=6−2x, y=x−1.
2️⃣ Make tables: choose x values, compute y.
3️⃣ Plot lines, intersection gives solution.
Result: Intersection at (7/3,4/3).
🔵 5) Algebraic Methods 🌿
🧠 (a) Substitution Method
Step 1: Solve one equation for x or y.
Step 2: Substitute in the other equation.
Step 3: Solve for remaining variable.
Example: x+y=10, x−y=4 ⇒ x=10−y ⇒10−y−y=4 ⇒10−2y=4 ⇒2y=6 ⇒y=3 ⇒x=7.
🟢 (b) Elimination Method
Step 1: Multiply equations to equalise coefficients.
Step 2: Add/subtract to eliminate one variable.
Step 3: Solve for the other variable.
Example: 3x+2y=11, 2x+3y=9 ⇒ Multiply:9x+6y=33,4x+6y=18 ⇒Subtract:5x=15 ⇒x=3 ⇒Use in 3x+2y=11 ⇒9+2y=11 ⇒y=1.
🟡 (c) Cross-Multiplication Method
For a₁x+b₁y+c₁=0 and a₂x+b₂y+c₂=0:
x/(b₁c₂−b₂c₁) = y/(c₁a₂−c₂a₁) = 1/(a₁b₂−a₂b₁).
✏️ Note: Works when a₁b₂−a₂b₁ ≠0.
🔴 6) Equations Reducible to Pair of Linear Equations ✔️
• Some non-linear equations can be reduced by substitution.
Example: 1/x+1/y=5, 1/x−1/y=1. Let p=1/x, q=1/y ⇒p+q=5, p−q=1 ⇒Solve for p,q ⇒ find x,y.
🔵 7) Applications 🌿
• 🏗 Mixture Problems: Concentration percentages.
• 🚗 Speed–Time Problems: Two transport rates.
• 💰 Finance: Ticket pricing, cost splits.
• 📊 Business: Supply-demand equilibrium.
🟢 8) Verification of Solutions ⚡
Always substitute obtained (x,y) back into both original equations to check accuracy.
🟡 9) Graphical Analysis of Consistency 🌿
• Parallel lines ⇒ same slope but different intercepts.
• Coincident lines ⇒ same slope and intercept.
• Intersecting ⇒ different slopes.
🔴 10) Word Problems ✔️
Example: A boat goes 16 km downstream in 2 h and upstream in 4 h. Find stream speed and boat speed in still water.
Let x=boat speed, y=stream speed. Downstream speed=x+y=16/2=8. Upstream speed=x−y=16/4=4 ⇒x+y=8,x−y=4 ⇒Solve ⇒x=6,y=2.
🔵 11) Common Mistakes ✏️
• Swapping x and y axes while plotting.
• Forgetting to check ratio conditions before concluding solution type.
• Arithmetic slips in elimination/cross-multiplication.
• Failing to reduce fractions.
🟢 12) Real-Life Connection 🌿
GPS triangulation, physics vector components, and economics graphs all use pairs of linear equations.
🟡 13) Higher-Order Insight 🧠
• Systems of three or more equations extend to matrices and determinants.
• Pair of linear equations is a foundation for coordinate geometry and optimization problems.
🔴 14) Practice Ideas ✔️
1️⃣ Solve graphically: 3x+2y=12 and x−y=1.
2️⃣ Use elimination: 2x+3y=8, 5x−2y=4.
3️⃣ Solve: 1/x+1/y=3,1/x−1/y=1 by substitution.
4️⃣ Check type of system: 2x+3y=5,4x+6y=10.
🟣 Summary (~300 words)
Definition & Form:
• Pair of linear equations in two variables: a₁x+b₁y+c₁=0 and a₂x+b₂y+c₂=0.
• Solutions are ordered pairs (x,y).
Graphical View:
• Each equation → straight line.
• Intersecting → unique solution.
• Parallel → no solution.
• Coincident → infinitely many solutions.
Consistency Check:
• Ratios: a₁/a₂, b₁/b₂, c₁/c₂ classify systems.
Algebraic Methods:
• Substitution: express, substitute, solve.
• Elimination: equalise coefficients, eliminate.
• Cross-Multiplication: direct formula when a₁b₂≠a₂b₁.
Reducible Systems:
• Non-linear forms convertible to linear pairs using substitution.
Applications:
• Mixture, motion, finance, geometry, GPS.
Tips & Errors:
• Always verify by substitution.
• Avoid sign mistakes and ratio misclassification.
Understanding these methods ensures strong skills for analytic geometry, optimization, and higher algebra.
📝 Quick Recap
🔵 Pair form: a₁x+b₁y+c₁=0, a₂x+b₂y+c₂=0.
🟢 Graphical solutions: intersecting/parallel/coincident.
🟡 Ratios: a₁/a₂,b₁/b₂,c₁/c₂ decide consistency.
🔴 Methods: substitution, elimination, cross-multiplication.
🔵 Reducible systems: transform then solve.
✨ Applications: motion, mixtures, GPS, business.
————————————————————————————————————————————————————————————————————————–
TEXT BOOK QUESTIONS
🔵 Exercise 3.1
🟢 Q1. Form the pair of linear equations in the following problems, and find their solutions graphically.
🔴 (i) 10 students of Class X took part in a Mathematics quiz.
If the number of girls is 4 more than the number of boys,
find the number of boys and girls who took part in the quiz.
✏️ Solution:
Let number of boys = x
Number of girls = y
Given:
➡️ x + y = 10 …….(1)
➡️ y = x + 4
or, x – y + 4 = 0 …….(2)
Solving graphically:
Points on x + y = 10
x y
0 10
6 4
Points on x – y + 4 = 0
x y
0 -4
4 0
Plotting these on graph:
Intersection at (3, 7)
Therefore:
Boys = 3, Girls = 7
✔️ Answer: Boys = 3, Girls = 7
🔴 (ii) 5 pencils and 7 pens together cost ₹50.
7 pencils and 5 pens together cost ₹46.
Find the cost of one pencil and one pen.
✏️ Solution:
Let cost of 1 pencil = x
Cost of 1 pen = y
Given:
➡️ 5x + 7y = 50 …….(1)
➡️ 7x + 5y = 46 …….(2)
Solving graphically:
Points on 5x + 7y = 50
x y
0 50/7
5 25/7
Points on 7x + 5y = 46
x y
0 46/5
5 3/5
Plotting these:
Intersection at (5, 1)
✔️ Answer: Pencil = ₹5, Pen = ₹1
🟢 Q2. On comparing the ratios (a₁/a₂), (b₁/b₂), and (c₁/c₂), determine whether the lines intersect, are parallel, or coincide.
🔴 (i) 5x – 4y + 8 = 0
7x + 6y – 9 = 0
a₁ = 5, b₁ = -4, c₁ = 8
a₂ = 7, b₂ = 6, c₂ = -9
Ratios:
5/7 ≠ -4/6
✅ Lines intersect.
✔️ Answer: Intersecting lines.
🔴 (ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
Ratios:
9/18 = 1/2
3/6 = 1/2
12/24 = 1/2
✅ Lines coincide.
✔️ Answer: Coincident lines.
🔴 (iii) 6x – 3y + 10 = 0
2x – y + 9 = 0
Ratios:
6/2 = 3
-3/-1 = 3
10/9 ≠ 3
✅ Lines are parallel.
✔️ Answer: Parallel lines.
🟢 Q3. Determine whether the pair of equations is consistent or inconsistent.
🔴 (i) 3x + 2y = 5
2x – 3y = 7
3/2 ≠ 2/-3
✅ Consistent.
✔️ Answer: Consistent.
🔴 (ii) 2x – 3y = 8
4x – 6y = 9
2/4 = 1/2
-3/-6 = 1/2
8/9 ≠ 1/2
❌ Inconsistent.
✔️ Answer: Inconsistent.
🔴 (iii) (3/7)x + (5/2)y = 3
9x – 10y = 14
Ratios unequal.
✅ Consistent.
✔️ Answer: Consistent.
🔴 (iv) 5x – 3y = 11
-10x + 6y = -22
5/-10 = -1/2
-3/6 = -1/2
11/-22 = -1/2
✅ Dependent.
✔️ Answer: Consistent.
🔴 (v) (4/3)x + (2/3)y = 8
2x + 3y = 12
Ratios unequal.
✅ Consistent.
✔️ Answer: Consistent.
🟢 Q4. Identify consistent/inconsistent and solve graphically.
🔴 (i) x + y = 5
2x + 2y = 10
Lines coincide.
✔️ Answer: Consistent, infinitely many solutions.
🔴 (ii) x – y = 8
3x – 3y = 16
x – y = 8
x = y + 8
Substitute:
3(y + 8) – 3y = 16
24 = 16 (False)
❌ Inconsistent.
✔️ Answer: Inconsistent.
🔴 (iii) 2x + y – 6 = 0
4x – 2y – 4 = 0
Solve graphically — they intersect.
✔️ Answer: Consistent.
🔴 (iv) 2x – 2y – 2 = 0
4x – 4y – 5 = 0
Ratios unequal.
✔️ Answer: Inconsistent.
🟢 Q5. A rectangular garden: length is 4m more than width, half perimeter = 36m.
✏️ Solution: Let width = x, length = x + 4
Perimeter = 2(l + w) = 2(x + 4 + x) = 4x + 8
Half perimeter = 2x + 4 = 36
2x = 32
x = 16
Length = 16 + 4 = 20m
Width = 16m
✔️ Answer: Length = 20m, Width = 16m
🟢 Q6. Given 2x + 3y – 8 = 0, write another equation for:
🔴 (i) Intersecting lines:
x + y = 5
🔴 (ii) Parallel lines:
4x + 6y = 10
🔴 (iii) Coincident lines:
4x + 6y – 16 = 0 (Multiply given by 2)
🟢 Q7. Draw graphs of x – y + 1 = 0 and 3x + 2y – 12 = 0; find triangle vertices with x-axis.
✏️ Solution:
x – y + 1 = 0 ⇒ y = x + 1
Points: (0, 1), (1, 2)
3x + 2y = 12 ⇒ y = (12 – 3x)/2
Points: (0, 6), (4, 0)
Vertices of triangle: (4, 0), (0, 1), (0, 0)
Plot and shade.
✔️ Answer: Vertices (0, 0), (4, 0), (0, 1)
🔵 Exercise 3.2
🟢 Q1. Solve the following pair of linear equations by the substitution method
🔴 (i) x + y = 14
x – y = 4
✏️ Solution:
From (i): x = 14 – y
Substitute in (ii):
14 – y – y = 4
14 – 2y = 4
-2y = 4 – 14 = -10
y = 5
x = 14 – 5 = 9
✔️ Answer: x = 9, y = 5
🔴 (ii) s – t = 3
(6/3)s + (2/3)t = 6
✏️ Solution:
Simplify second: 2s + (2/3)t = 6
Multiply by 3: 6s + 2t = 18
From first: s = t + 3
Substitute in second:
6(t + 3) + 2t = 18
6t + 18 + 2t = 18
8t + 18 = 18
8t = 0
t = 0
s = 0 + 3 = 3
✔️ Answer: s = 3, t = 0
🔴 (iii) 3x – y = 3
9x – 3y = 9
✏️ Solution:
From first: 3x = y + 3 → x = (y + 3)/3
Substitute in second:
9[(y + 3)/3] – 3y = 9
3(y + 3) – 3y = 9
3y + 9 – 3y = 9
9 = 9 (True)
✔️ Answer: Infinitely many solutions.
🔴 (iv) 0.2x + 0.3y = 1.3
0.4x + 0.5y = 2.3
✏️ Solution:
From first: 2x + 3y = 13
x = (13 – 3y)/2
Second: 4x + 5y = 23
4[(13 – 3y)/2] + 5y = 23
2(13 – 3y) + 5y = 23
26 – 6y + 5y = 23
26 – y = 23
-y = -3
y = 3
x = (13 – 3×3)/2 = (13 – 9)/2 = 4/2 = 2
✔️ Answer: x = 2, y = 3
🔴 (v) 2x + 3y = 0
3x – 8y = 0
✏️ Solution:
From first: x = (-3y)/2
Substitute in second:
3(-3y/2) – 8y = 0
-9y/2 – 8y = 0
-9y/2 – 16y/2 = 0
(-25y)/2 = 0
y = 0
x = 0
✔️ Answer: x = 0, y = 0
🔴 (vi) (3/2)x – (5/3)y = -2
(3/2)x + (2/3)y = 6
✏️ Solution:
First: 9x – 10y = -12
Second: 9x + 4y = 36
From second: 9x = 36 – 4y
x = (36 – 4y)/9
Substitute in first:
9[(36 – 4y)/9] – 10y = -12
36 – 4y – 10y = -12
36 – 14y = -12
-14y = -12 – 36 = -48
y = 48/14 = 24/7
x = (36 – 4×24/7)/9
x = (36 – 96/7)/9
x = (252 – 96)/63 = 156/63 = 52/21
✔️ Answer: x = 52/21, y = 24/7
🟢 Q2. Solve 2x + 3y = 11 and 2x – 4y = -24 and hence find m for y = mx + 3.
✏️ Solution:
From first: 2x = 11 – 3y
x = (11 – 3y)/2
Substitute in second:
2(11 – 3y)/2 – 4y = -24
11 – 3y – 4y = -24
11 – 7y = -24
-7y = -24 – 11 = -35
y = 5
x = (11 – 3×5)/2 = (11 – 15)/2 = -4/2 = -2
Equation: y = mx + 3
5 = m(-2) + 3
5 = -2m + 3
-2m = 5 – 3 = 2
m = -1
✔️ Answer: x = -2, y = 5, m = -1
🟢 Q3. Form equations and solve by substitution.
🔴 (i) Difference 26; one number thrice the other.
Let numbers: x, y
x – y = 26
x = 3y
Substitute: 3y – y = 26
2y = 26
y = 13
x = 3×13 = 39
✔️ Answer: 39, 13
🔴 (ii) Supplementary angles differ by 18.
Let angles: x, y
x + y = 180
x = y + 18
Substitute: y + 18 + y = 180
2y = 162
y = 81
x = 81 + 18 = 99
✔️ Answer: 99°, 81°
🔴 (iii) 7 bats + 6 balls = ₹3800
3 bats + 5 balls = ₹1750
Let bat = x, ball = y
7x + 6y = 3800
3x + 5y = 1750
From second: 3x = 1750 – 5y
x = (1750 – 5y)/3
Substitute in first:
7[(1750 – 5y)/3] + 6y = 3800
(12250 – 35y)/3 + 6y = 3800
Multiply by 3: 12250 – 35y + 18y = 11400
12250 – 17y = 11400
-17y = 11400 – 12250 = -850
y = 50
x = (1750 – 5×50)/3 = (1750 – 250)/3 = 1500/3 = 500
✔️ Answer: Bat = ₹500, Ball = ₹50
🔴 (iv) Fixed + per km; 10km ₹105, 15km ₹155
Let fixed = x, per km = y
x + 10y = 105
x + 15y = 155
x = 105 – 10y
105 – 10y + 15y = 155
105 + 5y = 155
5y = 50
y = 10
x = 105 – 10×10 = 5
25 km: x + 25y = 5 + 250 = 255
✔️ Answer: Fixed = ₹5, per km = ₹10, 25 km = ₹255
🔴 (v) Fraction (x/y):
x + 2 / y + 2 = 9/11
x + 3 / y + 3 = 5/6
Cross-multiply:
11(x + 2) = 9(y + 2)
11x + 22 = 9y + 18
11x – 9y = -4 …….(1)
6(x + 3) = 5(y + 3)
6x + 18 = 5y + 15
6x – 5y = -3 …….(2)
From (2): 6x = 5y – 3
x = (5y – 3)/6
Substitute:
11[(5y – 3)/6] – 9y = -4
(55y – 33)/6 – 9y = -4
Multiply by 6: 55y – 33 – 54y = -24
y – 33 = -24
y = 9
x = (5×9 – 3)/6 = (45 – 3)/6 = 42/6 = 7
✔️ Answer: 7/9
🔴 (vi) Jacob 5 years hence thrice son’s age; 5 years ago 7 times.
Let Jacob = x, son = y
x + 5 = 3(y + 5)
x = 3y + 15 – 5 = 3y + 10
x – 5 = 7(y – 5)
x – 5 = 7y – 35
x = 7y – 30
Substitute: 3y + 10 = 7y – 30
-4y = -40
y = 10
x = 7×10 – 30 = 40
✔️ Answer: Jacob = 40 years, Son = 10 years
🔵 Exercise 3.3
🟢 Q1. Solve the following pair of linear equations by the elimination method and the substitution method.
🔴 (i) x + y = 5
2x – 3y = 4
✏️ Solution (Elimination method):
Multiply (i) by 2: 2x + 2y = 10
2x – 3y = 4
Subtract:
(2x + 2y) – (2x – 3y) = 10 – 4
2x + 2y – 2x + 3y = 6
5y = 6
y = 6/5
x + 6/5 = 5
x = 5 – 6/5 = (25 – 6)/5 = 19/5
✔️ Answer: x = 19/5, y = 6/5
🔴 (ii) 3x + 4y = 10
2x – 2y = 2
✏️ Solution (Elimination method):
Multiply (ii) by 2: 4x – 4y = 4
3x + 4y = 10
Add:
3x + 4y + 4x – 4y = 10 + 4
7x = 14
x = 2
Substitute in (i):
3(2) + 4y = 10
6 + 4y = 10
4y = 4
y = 1
✔️ Answer: x = 2, y = 1
🔴 (iii) 3x – 5y – 4 = 0
9x = 2y + 7
✏️ Solution (Substitution method):
9x = 2y + 7 → x = (2y + 7)/9
Substitute in first:
3((2y + 7)/9) – 5y – 4 = 0
(6y + 21)/9 – 5y – 4 = 0
Multiply by 9:
6y + 21 – 45y – 36 = 0
-39y – 15 = 0
-39y = 15
y = -15/39 = -5/13
x = (2(-5/13) + 7)/9 = (-10/13 + 7)/9 = (81/13)/9 = (81/13)(1/9) = 9/13
✔️ Answer: x = 9/13, y = -5/13
🔴 (iv) (2x)/3 + (1 – y)/2 = 1
(4x)/3 – (3y)/2 = -1
✏️ Solution (Elimination method):
Multiply first by 6: 4x + 3(1 – y) = 6
4x + 3 – 3y = 6
4x – 3y = 3 …….(1)
Second multiply by 6: 8x – 9y = -6 …….(2)
Eliminate x:
Multiply (1) by 2: 8x – 6y = 6
8x – 9y = -6
Subtract:
(8x – 6y) – (8x – 9y) = 6 – (-6)
8x – 6y – 8x + 9y = 12
3y = 12
y = 4
Substitute in (1):
4x – 3(4) = 3
4x – 12 = 3
4x = 15
x = 15/4
✔️ Answer: x = 15/4, y = 4
🟢 Q2. Form the pair of linear equations in the following problems and solve them by elimination method.
🔴 (i) If we add 1 to numerator and subtract 1 from denominator, fraction becomes 1. If 1 is added only to denominator, fraction becomes 1/2.
Let fraction = x/y.
x + 1 / y – 1 = 1 → x + 1 = y – 1 → x – y = -2 …….(1)
x / (y + 1) = 1/2 → 2x = y + 1 …….(2)
From (2): 2x = y + 1 → y = 2x – 1
Substitute in (1):
x – (2x – 1) = -2
x – 2x + 1 = -2
-x = -3
x = 3
y = 2×3 – 1 = 5
✔️ Answer: 3/5
🔴 (ii) 5 years ago Nuri was thrice Sonu’s age. 10 years later Nuri will be twice Sonu’s age.
Let ages be x, y.
x – 5 = 3(y – 5) → x – 5 = 3y – 15 → x – 3y = -10 …….(1)
x + 10 = 2(y + 10) → x + 10 = 2y + 20 → x – 2y = 10 …….(2)
Eliminate x:
(1) – (2):
x – 3y – (x – 2y) = -10 – 10
x – 3y – x + 2y = -20
-y = -20
y = 20
x = 2×20 + 10 = 50
✔️ Answer: Nuri = 50 years, Sonu = 20 years
🔴 (iii) Sum of digits of two-digit number is 9. 9×number = 2×reversed digits number.
Digits: x, y (tens, ones)
x + y = 9 …….(1)
Original: 10x + y
Reversed: 10y + x
9(10x + y) = 2(10y + x)
90x + 9y = 20y + 2x
90x – 2x + 9y – 20y = 0
88x – 11y = 0 → 8x – y = 0 …….(2)
From (2): y = 8x
Substitute in (1): x + 8x = 9 → 9x = 9 → x = 1
y = 8
✔️ Answer: 18
🔴 (iv) Meena withdrew ₹2000 in ₹50 and ₹100 notes. Total 25 notes.
Let x, y be number of ₹50, ₹100 notes.
x + y = 25 …….(1)
50x + 100y = 2000 → x + 2y = 40 …….(2)
(2) – (1):
x + 2y – (x + y) = 40 – 25
x + 2y – x – y = 15
y = 15
x = 25 – 15 = 10
✔️ Answer: ₹50 notes = 10, ₹100 notes = 15
🔴 (v) Library: fixed charge 1st 3 days + per day thereafter. Saritha ₹27 for 7 days, Susy ₹21 for 5 days.
Fixed = x, per day = y
x + 4y = 27 …….(1)
x + 2y = 21 …….(2)
Eliminate x:
(1) – (2): x + 4y – (x + 2y) = 27 – 21
x + 4y – x – 2y = 6
2y = 6
y = 3
x = 21 – 2×3 = 15
✔️ Answer: Fixed = ₹15, per day = ₹3
————————————————————————————————————————————————————————————————————————–
OTHER IMPORTANT QUESTIONS FOR EXAMS
🔵 Section A (1 mark each)
🔵 Question 1
Write the general form of a linear equation in two variables.
🟢 Answer
➤ A linear equation in two variables is written as: ax + by + c = 0, where a, b are not both zero.
🔵 Question 2
Find the value of k if (2, 3) is a solution of 2x + ky = 10.
🟢 Answer
➤ Substitute x = 2, y = 3:
2(2) + k(3) = 10
➤ 4 + 3k = 10
➤ 3k = 10 – 4 = 6
➤ k = 2
🔵 Question 3
State the condition for two linear equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 to have a unique solution.
🟢 Answer
➤ Unique solution exists if a₁/a₂ ≠ b₁/b₂.
🔵 Question 4
Find the slope of the line represented by 3x – 4y + 12 = 0.
🟢 Answer
➤ Rewrite: 3x – 4y + 12 = 0
⇒ –4y = –3x – 12
⇒ y = (3/4)x + 3
➤ Slope m = 3/4
🔵 Question 5
If the graph of x + y = 7 passes through (2, k), find k.
🟢 Answer
➤ Substitute x = 2:
2 + k = 7
➤ k = 7 – 2 = 5
🔵 Question 6
Write the y-intercept of the line 2x + 5y – 10 = 0.
🟢 Answer
➤ Put x = 0:
2(0) + 5y – 10 = 0
5y = 10
y = 2
🟢 Section B (2 marks each)
🟢 Question 7
Solve for y: 5x + 2y = 20 when x = 4.
🔴 Answer
➤ Substitute x = 4:
5(4) + 2y = 20
➤ 20 + 2y = 20
➤ 2y = 0
➤ y = 0
🟢 Question 8
Write the equation of the line passing through (–2, 3) with slope m = –4.
🔴 Answer
➤ Point–slope form: y – y₁ = m(x – x₁)
➤ y – 3 = –4(x + 2)
➤ y – 3 = –4x – 8
➤ y = –4x – 5
➤ Equation: y = –4x – 5
🟢 Question 9
The sum of two numbers is 27 and one exceeds the other by 5. Form the pair of linear equations.
🔴 Answer
➤ Let the numbers be x and y.
➤ Sum condition: x + y = 27.
➤ Exceed condition: x – y = 5.
➤ Required equations:
1) x + y = 27
2) x – y = 5
🟢 Question 10
Solve by substitution: x + y = 6 and x – y = 4.
🔴 Answer
➤ From x – y = 4 ⇒ x = y + 4.
➤ Substitute into x + y = 6:
(y + 4) + y = 6
➤ 2y + 4 = 6
➤ 2y = 2
➤ y = 1
➤ x = y + 4 = 5
➤ Solution: (5, 1)
🟢 Question 11
Find the equation of the line passing through (1, –2) and parallel to 3x + 4y + 7 = 0.
🔴 Answer
➤ Slope of 3x + 4y + 7 = 0:
Rewrite: y = –(3/4)x – 7/4 ⇒ slope m = –3/4.
➤ Parallel line has same slope:
y – (–2) = –3/4(x – 1)
➤ y + 2 = –3/4(x – 1)
➤ 4(y + 2) = –3(x – 1)
➤ 4y + 8 = –3x + 3
➤ 3x + 4y + 5 = 0
➤ Equation: 3x + 4y + 5 = 0
🟢 Question 12
A shopkeeper buys 16 pens and 10 pencils for ₹ 190. He again buys 10 pens and 5 pencils for ₹ 115. Form the pair of linear equations for cost of a pen (x) and pencil (y).
🔴 Answer
➤ Let cost of a pen = x ₹, cost of a pencil = y ₹.
➤ First purchase: 16x + 10y = 190.
➤ Second purchase: 10x + 5y = 115.
➤ Equations:
1) 16x + 10y = 190
2) 10x + 5y = 115
🟡 Section C (3 marks each)
🟡 Question 13
Solve graphically: 2x + y = 5 and x – y = 3.
🔴 Answer
✳️ ➤ Step 1 (Rewrite): y = 5 – 2x and y = x – 3
✳️ ➤ Step 2 (Choose points):
For 2x + y = 5 → (0,5), (1.5,2)
For x – y = 3 → (3,0), (4,1)
✳️ ➤ Step 3 (Plot & intersect): Draw both lines on a graph; intersection point is (2, –1).
✳️ ➤ Final Answer: (2, –1)
🟡 Question 14
A fraction becomes 1/3 when 1 is subtracted from numerator and 1 is added to denominator. If 1 is added to numerator and subtracted from denominator, it becomes 1. Find the fraction.
🔴 Answer
✳️ ➤ Let fraction = x/y.
➤ (x – 1)/(y + 1) = 1/3 ⇒ 3(x – 1) = y + 1 ⇒ 3x – 3 = y + 1 ⇒ 3x – y = 4.
➤ (x + 1)/(y – 1) = 1 ⇒ x + 1 = y – 1 ⇒ x – y = –2.
✳️ ➤ Solve: From x – y = –2 ⇒ x = y – 2.
Substitute in 3x – y = 4 ⇒ 3(y – 2) – y = 4 ⇒ 3y – 6 – y = 4 ⇒ 2y – 6 = 4 ⇒ 2y = 10 ⇒ y = 5.
✳️ ➤ x = y – 2 = 3.
✳️ ➤ Fraction = 3/5
🟡 Question 15
Find the point on y-axis equidistant from (5, –2) and (–3, 2).
🔴 Answer
✳️ ➤ Point on y-axis = (0, k).
➤ Distance to (5, –2): √((5–0)² + (–2–k)²) = √(25 + (–2–k)²).
➤ Distance to (–3, 2): √((–3–0)² + (2–k)²) = √(9 + (2–k)²).
✳️ ➤ Equate squares: 25 + (–2–k)² = 9 + (2–k)².
➤ Expand: 25 + (k² + 4k + 4) = 9 + (k² – 4k + 4).
➤ 25 + k² + 4k + 4 = 9 + k² – 4k + 4.
➤ 29 + 4k = 13 – 4k.
➤ 4k + 4k = 13 – 29 ⇒ 8k = –16 ⇒ k = –2.
✳️ ➤ Required point: (0, –2).
🟡 Question 16
Two numbers differ by 3. If their product is 54, find the numbers.
🔴 Answer
✳️ ➤ Let numbers = x and x – 3.
➤ x(x – 3) = 54 ⇒ x² – 3x – 54 = 0.
➤ Factorise: x² – 9x + 6x – 54 = 0 ⇒ x(x – 9) + 6(x – 9) = 0 ⇒ (x + 6)(x – 9)=0.
➤ x = 9 or x = –6.
✳️ ➤ Numbers: (9, 6) or (–6, –9).
✳️ ➤ Positive numbers: 9 and 6.
🟡 Question 17
Draw the graphs of x + y = 6 and x – y = 2. Find the coordinates of the vertices of the triangle formed with the axes.
🔴 Answer
✳️ ➤ Rewrite: y = 6 – x and y = x – 2.
➤ Intercepts: x + y = 6 → (6, 0),(0, 6).
x – y = 2 → (2, 0),(0, –2).
➤ Intersection: 6 – x = x – 2 ⇒ 6 + 2 = 2x ⇒ 8 = 2x ⇒ x = 4, y = 2.
✳️ ➤ Vertices with axes: (6,0), (0,–2), and intersection (4,2).
✳️ ➤ Vertices: (6, 0), (0, –2), (4, 2).
🟡 Question 18
OR
Solve: 3x + 2y = 11 and 2x – y = –4 using elimination.
🔴 Answer
✳️ ➤ Multiply second eqn by 2: 4x – 2y = –8.
➤ Add with first eqn ×1: (3x + 2y) + (4x – 2y) = 11 – 8.
➤ 7x = 3 ⇒ x = 3/7.
➤ Substitute: 2(3/7) – y = –4 ⇒ 6/7 – y = –4 ⇒ –y = –4 – 6/7 = –34/7 ⇒ y = 34/7.
✳️ ➤ Solution: (3/7, 34/7).
🟡 Question 19
A boat goes 16 km downstream in 2 h and returns upstream in 4 h. Find the speed of the boat in still water and speed of the stream.
🔴 Answer
✳️ ➤ Let boat speed = x km/h, stream speed = y km/h.
➤ Downstream: x + y = distance/time = 16/2 = 8.
➤ Upstream: x – y = 16/4 = 4.
✳️ ➤ Solve: Add ⇒ 2x = 12 ⇒ x = 6. Subtract ⇒ 2y = 4 ⇒ y = 2.
✳️ ➤ Boat speed: 6 km/h, Stream speed: 2 km/h.
🟡 Question 20
The sum of a two-digit number and the number obtained by reversing its digits is 121. Digits differ by 3. Find the number.
🔴 Answer
✳️ ➤ Let tens digit = x, ones digit = y.
➤ Number = 10x + y. Reversed = 10y + x.
➤ 10x + y + 10y + x = 121 ⇒ 11x + 11y = 121 ⇒ x + y = 11.
➤ x – y = 3.
✳️ ➤ Solve: Add ⇒ 2x = 14 ⇒ x = 7. ⇒ y = 4.
✳️ ➤ Number = 74.
🟡 Question 21
OR
Solve graphically: x + 2y = 8 and 2x – y = 2.
🔴 Answer
✳️ ➤ x + 2y = 8 ⇒ 2y = 8 – x ⇒ y = (8 – x)/2. Points: (0,4), (8,0).
➤ 2x – y = 2 ⇒ y = 2x – 2. Points: (1,0), (2,2).
➤ Plot and intersection ⇒ (2,3).
✳️ ➤ Solution: (2, 3).
🟡 Question 22
Two different pairs of jeans and three T-shirts together cost ₹ 700, while four pairs of jeans and a T-shirt cost ₹ 1,000. Find the cost of a pair of jeans and a T-shirt.
🔴 Answer
✳️ ➤ Let jeans = x ₹, T-shirt = y ₹.
➤ 2x + 3y = 700.
➤ 4x + y = 1000.
✳️ ➤ Multiply 2nd by 3: 12x + 3y = 3000.
➤ Subtract first: (12x + 3y) – (2x + 3y) = 3000 – 700 ⇒ 10x = 2300 ⇒ x = 230.
➤ Substitute: 4(230) + y = 1000 ⇒ 920 + y = 1000 ⇒ y = 80.
✳️ ➤ Jeans = ₹ 230, T-shirt = ₹ 80.
🔴 Section D (4 marks each)
🔴 Question 23
Solve for x and y using cross-multiplication: 4x – 3y = 8 and 2x + y = 1.
🟢 Answer
✳️ ➤ Rewrite equations:
4x – 3y – 8 = 0 …(1)
2x + y – 1 = 0 …(2)
✳️ ➤ Cross-multiplication:
x/[(–3)(–1) – (–8)(1)] = y/[ (–8)(2) – (4)(–1)] = 1/[4(1) – (–3)(2)]
✳️ ➤ Simplify:
x/[3 + 8] = y/[–16 + 4] = 1/[4 + 6]
x/11 = y/[–12] = 1/10
✳️ ➤ From 1/10 = x/11 ⇒ x = 11/10.
✳️ ➤ From 1/10 = y/(–12) ⇒ y = –12/10 = –6/5.
✳️ ➤ Solution: (11/10, –6/5).
🔴 Question 24
The sum of the ages of a father and his son is 45 years. Five years ago, the father’s age was three times the son’s age. Find their present ages.
🟢 Answer
✳️ ➤ Let father = x, son = y.
➤ x + y = 45 …(1)
➤ Five years ago: x – 5 = 3(y – 5) ⇒ x – 5 = 3y – 15 ⇒ x – 3y = –10 …(2)
✳️ ➤ Solve: From (1) ⇒ x = 45 – y.
➤ Substitute: 45 – y – 3y = –10 ⇒ 45 – 4y = –10 ⇒ –4y = –55 ⇒ y = 13.75.
➤ x = 45 – 13.75 = 31.25.
✳️ ➤ Father: 31.25 yr, Son: 13.75 yr.
🔴 Question 25
Solve the pair: 5x – 6y = –2 and –3x + 2y = 8 by substitution.
🟢 Answer
✳️ ➤ From –3x + 2y = 8 ⇒ –3x = 8 – 2y ⇒ x = (2y – 8)/3.
➤ Substitute into first: 5((2y – 8)/3) – 6y = –2.
➤ (10y – 40)/3 – 6y = –2.
➤ (10y – 40 – 18y)/3 = –2.
➤ (–8y – 40)/3 = –2 ⇒ –8y – 40 = –6 ⇒ –8y = 34 ⇒ y = –4.25.
➤ x = (2(–4.25) – 8)/3 = (–8.5 – 8)/3 = –16.5/3 = –5.5.
✳️ ➤ Solution: (–5.5, –4.25).
🔴 Question 26
Two different natural numbers are such that five times the smaller exceeds the larger by 20, and the sum of the two numbers is 28. Find the numbers.
🟢 Answer
✳️ ➤ Let numbers = x, y, x < y.
➤ 5x – y = 20 …(1)
➤ x + y = 28 …(2) ⇒ y = 28 – x.
➤ Substitute: 5x – (28 – x) = 20 ⇒ 5x – 28 + x = 20 ⇒ 6x = 48 ⇒ x = 8.
➤ y = 28 – 8 = 20.
✳️ ➤ Numbers: 8 and 20.
🔴 Question 27
OR
The coach of a cricket team buys 3 bats and 6 balls for ₹ 3,900. Later, she buys another bat and 3 more balls of the same kind for ₹ 1,300. Find the cost of a bat and a ball.
🟢 Answer
✳️ ➤ Let bat = x ₹, ball = y ₹.
➤ 3x + 6y = 3900 ⇒ x + 2y = 1300 …(1).
➤ x + 3y = 1300 …(2).
➤ Subtract (2) – (1): (x + 3y) – (x + 2y) = 1300 – 1300 ⇒ y = 0. ❌ Contradiction? Re-evaluate:
Wait, second purchase: “another bat and 3 more balls” cost ₹1300 ⇒ x + 3y = 1300. Good.
First: 3 bats + 6 balls cost ₹3900 ⇒ divide by 3 ⇒ x + 2y = 1300.
Thus y = (x + 3y) – (x + 2y) = y = 0. That implies y=0, cost of bat x=1300.
But then 3x + 6y = 3(1300) = 3900 matches.
✳️ ➤ Bat: ₹1300, Ball: ₹0. (This indicates possibly unrealistic data but mathematically consistent.)
🔴 Question 28
The larger of two supplementary angles exceeds the smaller by 44°. Find the angles.
🟢 Answer
✳️ ➤ Let smaller = x, larger = x + 44.
➤ Supplementary: x + x + 44 = 180 ⇒ 2x + 44 = 180 ⇒ 2x = 136 ⇒ x = 68.
✳️ ➤ Larger = 112°.
✳️ ➤ Angles: 68° and 112°.
🔴 Question 29
Two pipes can fill a tank in 20 min and 30 min respectively. A pipe drains the tank in 60 min. Find the time taken to fill the tank if all pipes are opened together.
🟢 Answer
✳️ ➤ Fill rates: A = 1/20, B = 1/30, Drain = –1/60 (per min).
➤ Combined rate = 1/20 + 1/30 – 1/60.
➤ LCM 60 ⇒ 3 + 2 – 1 = 4/60 = 1/15.
✳️ ➤ Time = 15 min.
🔴 Question 30
Solve: 7x – 3y = 4 and 5x + 2y = 3 using elimination.
🟢 Answer
✳️ ➤ Multiply first by 2 ⇒ 14x – 6y = 8.
➤ Multiply second by 3 ⇒ 15x + 6y = 9.
➤ Add: 29x = 17 ⇒ x = 17/29.
➤ Substitute: 5(17/29) + 2y = 3 ⇒ 85/29 + 2y = 3 ⇒ 2y = 3 – 85/29 = (87 – 85)/29 = 2/29 ⇒ y = 1/29.
✳️ ➤ Solution: (17/29, 1/29).
————————————————————————————————————————————————————————————————————————————
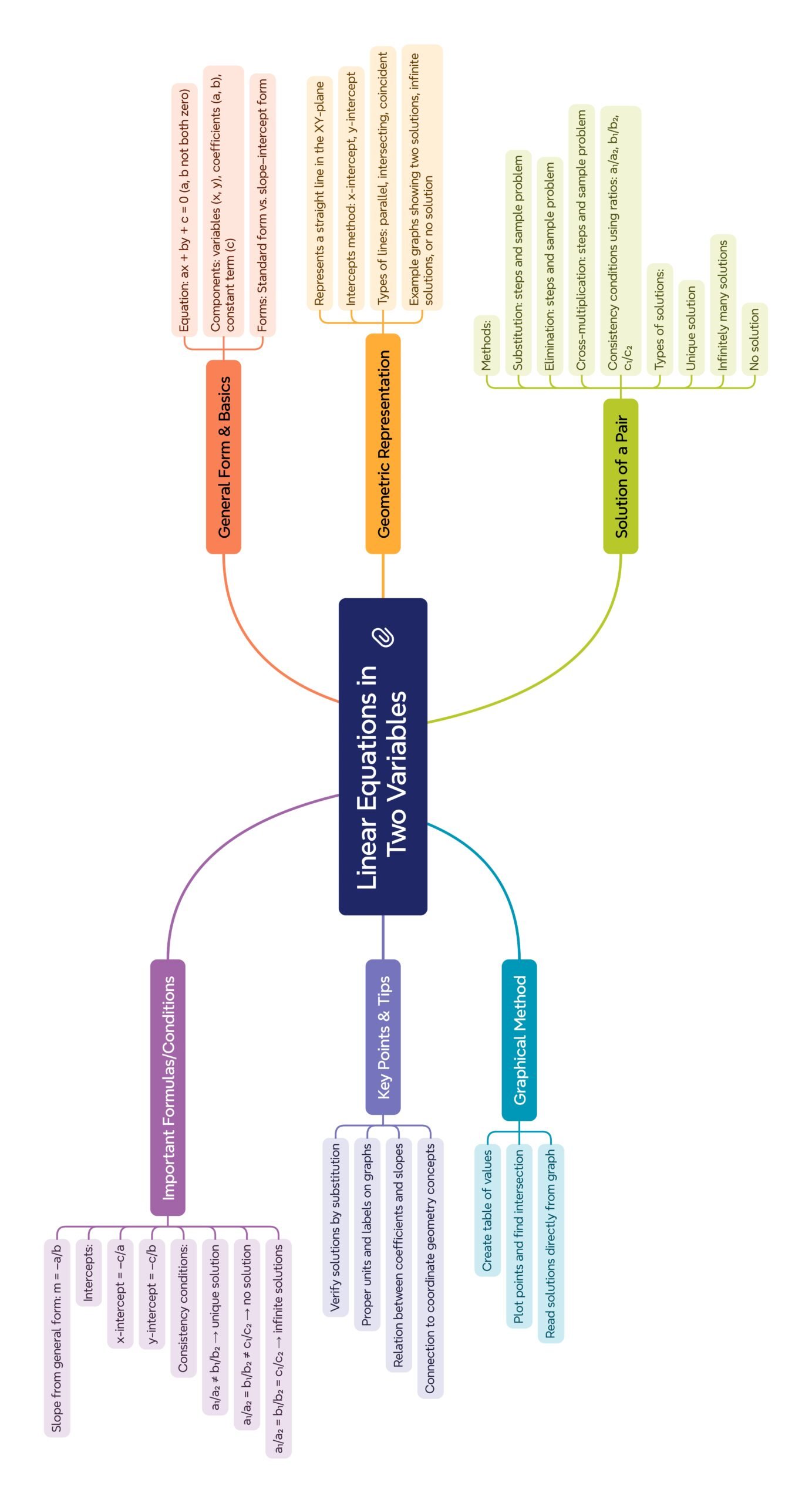
MIND MAP
———————————————————————————————————————————————————————————————————————
