Class 10 : Maths (In English) – Lesson 14. Probability
EXPLANATION & SUMMARY
🔵 📜 Introduction
• Probability quantifies the likelihood of an event.
• It is the ratio of favourable outcomes to total equally likely outcomes.
• Everyday examples: tossing coins, rolling dice, drawing cards, weather forecasts, quality control.
🟢 💡 Key Terms
• Experiment: An action with uncertain outcome (e.g., tossing a die).
• Sample space (S): Set of all possible outcomes. Example: Tossing a coin → S = {H,T}.
• Event (E): A subset of the sample space. Example: Getting an even number on a die → E = {2,4,6}.
• Favourable outcomes: Elements of S that satisfy E.
• Equally likely outcomes: All outcomes have equal chance.
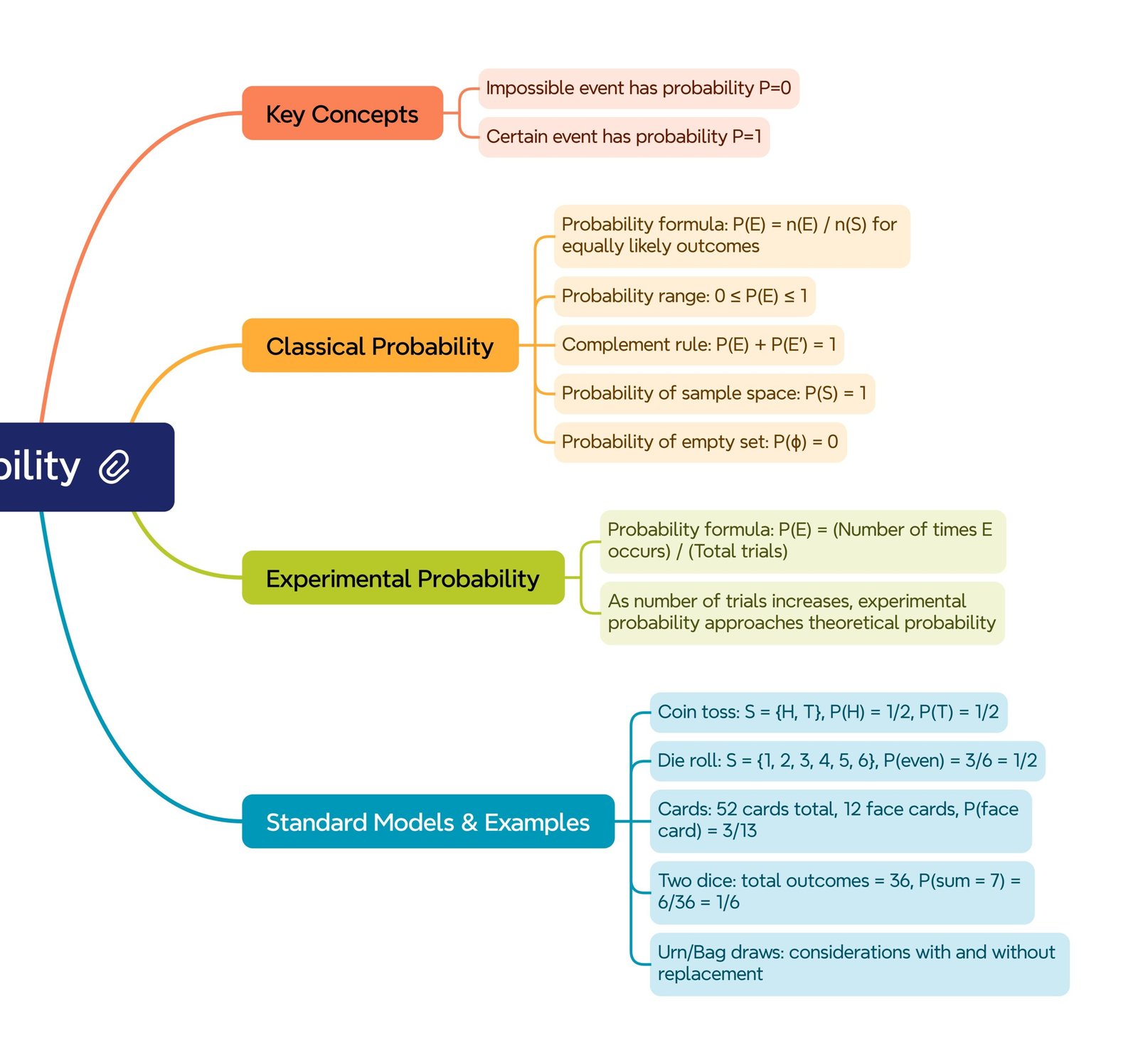
• Impossible event: Probability = 0.
• Certain event: Probability = 1.
🔴 🧭 Classical Definition of Probability
✔️ Formula: P(E) = n(E) / n(S)
- n(E) = number of favourable outcomes.
- n(S) = total number of equally likely outcomes.
💡 Example: Tossing a die, probability of even number: n(E)=3 (2,4,6), n(S)=6.
➡️ P(E)=3/6 = 1/2.
🟡 📌 Properties of Probability
• 0 ≤ P(E) ≤ 1 for any event E.
• P(S)=1.
• P(ϕ)=0 (ϕ = impossible event).
• For complementary events: P(E)+P(E’)=1.
• For mutually exclusive exhaustive events: Sum of probabilities = 1.
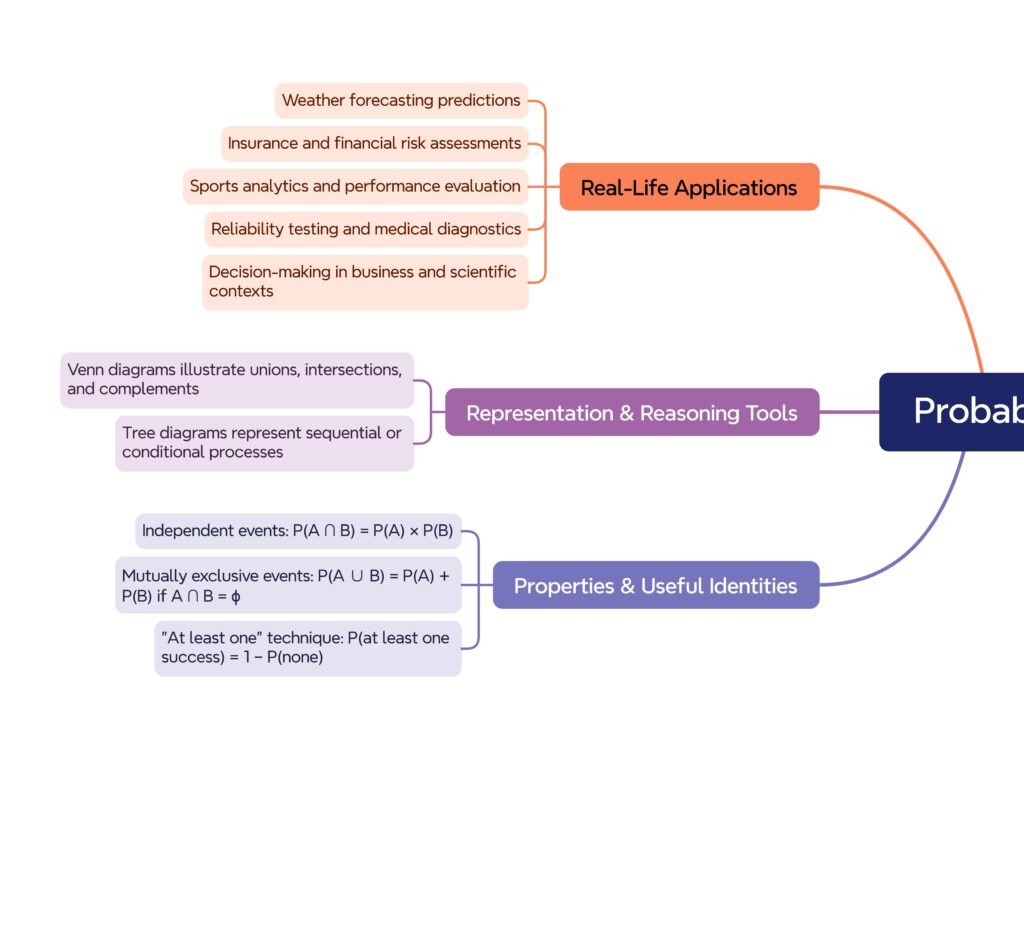
🟢 🎨 Visual Representation
• Probability distributions can be shown with bar graphs or pie charts.
• Venn diagrams illustrate complementary or mutually exclusive events.
📚 Section A – Basic Examples
🔵 Example 1: Coin Toss
Q: Find the probability of getting a head.
Solution: S={H,T}, n(S)=2.
Favourable: E={H}, n(E)=1.
➡️ P(E)=1/2.
🟢 Example 2: Rolling a Die
Q: Probability of number <4.
S={1,2,3,4,5,6}, n(S)=6.
E={1,2,3}, n(E)=3.
➡️ P(E)=3/6 = 1/2.
🔴 Example 3: Drawing a Card
Q: Probability of drawing a king.
Total cards=52.
Kings=4.
➡️ P(E)=4/52 = 1/13.
🟡 Example 4: Complementary Events
Q: Probability of NOT drawing a heart.
P(heart)=13/52=1/4.
➡️ P(not heart)=1−1/4=3/4.
🧭 Section B – Theoretical Concepts
🔵 1. Equally Likely vs Unequally Likely Events
• Equally likely: Tossing a fair coin.
• Unequally likely: Drawing a specific colour from a biased bag.
🟢 2. Independent vs Dependent Events
• Independent: Tossing two separate coins—outcome of one does not affect the other.
• Dependent: Drawing two cards without replacement—first draw affects second.
🔴 3. Experimental Probability
• P(E)= (Number of times E occurs)/(Total trials).
• As trials → ∞, experimental probability → theoretical probability.
🟡 4. Complementary Events in Real Life
• Weather forecast: P(rain)=0.3 → P(no rain)=0.7.
• Machine reliability: P(failure)=0.02 → P(success)=0.98.
📊 Section C – Advanced Examples
🔵 Example 5: Two Dice
Q: Probability of sum = 7.
Sample space outcomes=36.
Favourable pairs=(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)=6.
➡️ P(E)=6/36=1/6.
🟢 Example 6: Bag of Balls
Bag contains 5 red, 3 blue, 2 green balls. Draw one ball.
Total=10. P(red)=5/10=1/2.
P(not green)=1−2/10=8/10=4/5.
🔴 Example 7: Deck of Cards
Q: Probability of face card (J,Q,K).
Face cards=12.
➡️ P(E)=12/52=3/13.
🟡 Example 8: Coin + Die
Sample space size=2×6=12.
Q: Probability of getting head and even number.
Favourable outcomes=(H,2),(H,4),(H,6)=3.
➡️ P(E)=3/12=1/4.
🧮 Section D – Applications
🔵 1. Quality Control
Factories use probability to estimate defective rates.
Example: If 2% defective, probability next piece is defective=0.02.
🟢 2. Insurance & Finance
Insurance premiums calculated using probability of risk events.
🔴 3. Games of Chance
Lottery, cards, dice—all probability-based.
🟡 4. Data Science & Forecasting
Predictive models rely on probability distributions.
🧾 Important Formulas (Copy-Paste Friendly)
✔️ P(E)=n(E)/n(S)
✔️ 0 ≤ P(E) ≤ 1
✔️ P(E)+P(E’)=1
✔️ For two independent events A,B: P(A∩B)=P(A)×P(B)
✔️ For mutually exclusive events: P(A∪B)=P(A)+P(B)
✔️ Empirical probability: P(E)= (Number of successful trials)/(Total trials)
🖌 Tips for Graphical Questions
🔵 Histograms for Probability Distributions
• Bars touch (continuous data).
• Use class boundaries on x-axis.
🟢 Probability Trees
• Tree diagrams help visualize multi-step experiments.
🔴 Venn Diagrams
• Show unions, intersections, complements.
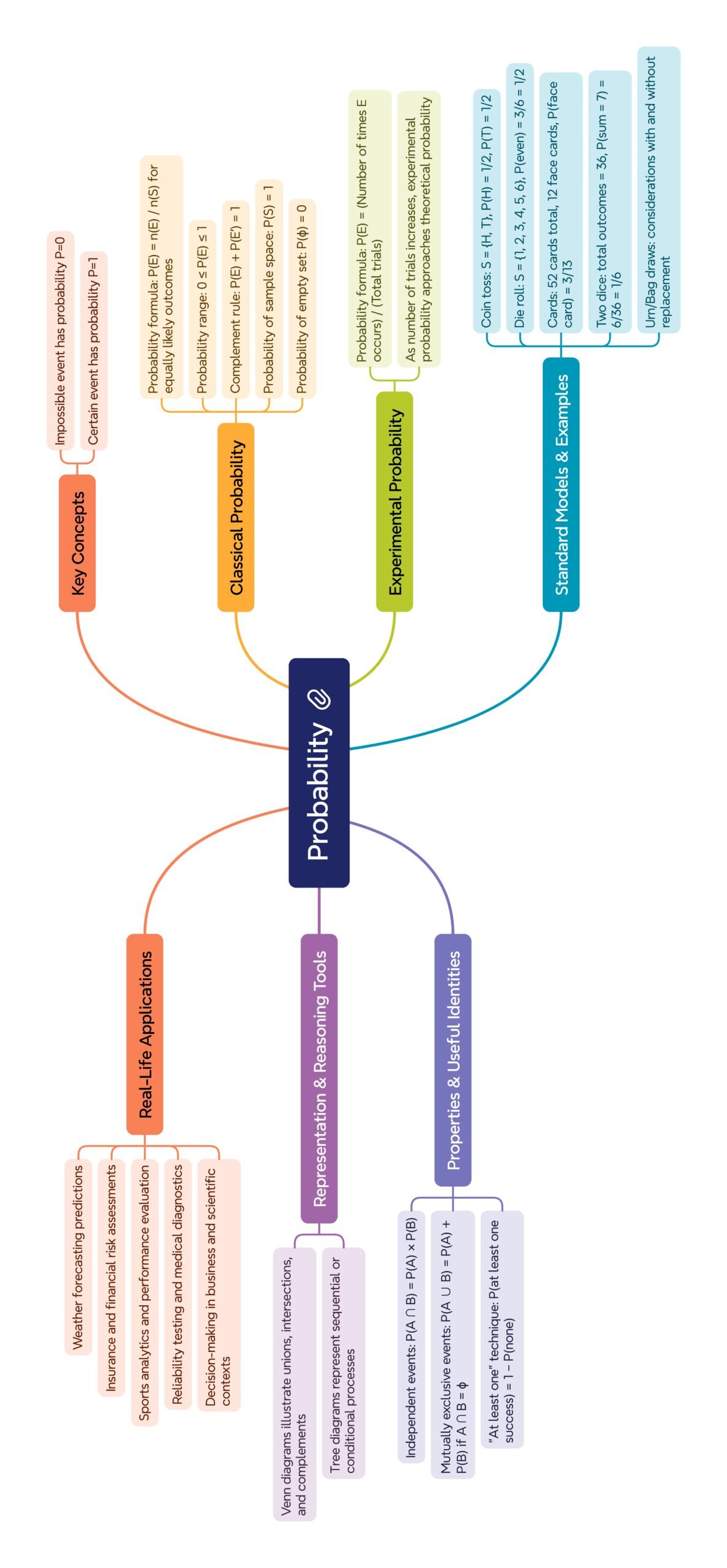
🧭 Real-Life Scenarios
🟢 Weather Prediction: Probability of rain helps farmers plan.
🔵 Sports Analytics: Cricket: P(player scores > 50) guides strategies.
🔴 Medical Testing: Sensitivity and specificity use probability.
🟡 Risk Management: Businesses estimate losses.
✨ Summary (~300 words)
📌 Probability quantifies uncertainty using the ratio of favourable to total equally likely outcomes.
📌 Key terms: experiment, sample space, event, equally likely outcomes.
📌 Classical probability formula: P(E)=n(E)/n(S).
📌 Properties: 0 ≤ P(E) ≤ 1, P(S)=1, P(ϕ)=0, complementary events sum to 1.
📌 Experimental probability approaches theoretical values as trials increase.
📌 Common models: coins, dice, cards, urn problems.
📌 Advanced use cases: quality control, insurance, finance, sports analytics, weather forecasting.
📌 Graphical tools: histograms, frequency polygons, ogives, tree diagrams, and Venn diagrams help visualize probabilities.
📌 Formulas:
– P(E)+P(E’)=1
– P(A∩B)=P(A)×P(B) (independent events)
– P(A∪B)=P(A)+P(B) (mutually exclusive events)
– Empirical probability=successful trials/total trials
📌 Remember to express answers as fractions or simplified decimals. Use consistent SI units for measurements when relevant.
📌 Probability bridges pure mathematics and real-world decision-making, underpinning statistics, risk analysis, AI, and finance.
📝 Quick Recap
• 🎲 Probability = favourable/total outcomes.
• 🃏 0 ≤ P(E) ≤ 1; complements sum to 1.
• 🧭 Classical vs experimental probability.
• 📊 Tools: histograms, ogives, Venn diagrams.
• 📈 Applications: weather, games, insurance, science.
———————————————————————————————————————————————————————————————————————————–
TEXT BOOK QUESTIONS
📘 PROBABILITY — EXERCISE 14.1
🔵 Question 1: Complete the following statements:
(i) Probability of an event E + Probability of the event “not E” = ________.
(ii) The probability of an event that cannot happen is ________. Such an event is called ________.
(iii) The probability of an event that is certain to happen is ________. Such an event is called ________.
(iv) The sum of the probabilities of all the elementary events of an experiment is ________.
(v) The probability of an event is greater than or equal to ________ and less than or equal to ________.
🟢 Answer:
(i) ✔️ 1
(ii) ✔️ 0 ➡️ Impossible event
(iii) ✔️ 1 ➡️ Certain event
(iv) ✔️ 1
(v) ✔️ 0 ➡️ and ➡️ 1
🔵 Question 2: Which of the following experiments have equally likely outcomes? Explain.
(i) A driver attempts to start a car. The car starts or does not start.
(ii) A player attempts to shoot a basketball. She/he shoots or misses the shot.
(iii) A trial is made to answer a true–false question. The answer is right or wrong.
(iv) A baby is born. It is a boy or a girl.
🟢 Answer:
• (i) ❌ Not equally likely—starting depends on car condition.
• (ii) ❌ Not equally likely—depends on player’s skill.
• (iii) ✔️ Equally likely—True or False are equally probable.
• (iv) ✔️ Equally likely—Boy or girl (ignoring minor biases) ≈ equal chance.
🔵 Question 3: Why is tossing a coin considered a fair way of deciding which team should get the ball at the beginning of a football game?
🟢 Answer:
✔️ Because two outcomes (H,T) are equally likely and neither team has an advantage—probability(H)=probability(T)=1/2.
🔵 Question 4: Which of the following cannot be the probability of an event?
(A) 2/3 (B) –1.5 (C) 15% (D) 0.7
🟢 Answer:
✔️ (B) –1.5 ❌ (probability cannot be negative).
🔵 Question 5: If P(E)=0.05, what is the probability of “not E”?
🟢 Answer:
✔️ P(not E)=1–P(E)=1–0.05=0.95.
🔵 Question 6: A bag contains lemon flavoured candies only. Malini takes out one candy without looking into the bag. What is the probability that she takes out
(i) an orange flavoured candy?
(ii) a lemon flavoured candy?
🟢 Answer:
• (i) ✔️ 0 (impossible event).
• (ii) ✔️ 1 (certain event).
🔵 Question 7: It is given that in a group of 3 students, the probability of 2 students not having the same birthday is 0.992. What is the probability that the 2 students have the same birthday?
🟢 Answer:
✔️ P(same birthday)=1–0.992=0.008.
🔵 Question 8: A bag contains 3 red balls and 5 black balls. A ball is drawn at random. What is the probability that the ball drawn is
(i) red? (ii) not red?
🟢 Answer:
Total=3+5=8.
• (i) P(red)=3/8.
• (ii) P(not red)=1–3/8=5/8.
🔵 Question 9: A box contains 5 red marbles, 8 white marbles, and 4 green marbles. One marble is taken at random. Find the probability that it is
(i) red? (ii) white? (iii) not green?
🟢 Answer:
Total=5+8+4=17.
• (i) P(red)=5/17.
• (ii) P(white)=8/17.
• (iii) P(not green)=1–P(green)=1–4/17=13/17.
🔵 Question 10: A piggy bank contains 100 fifty-paise coins, 50 one-rupee coins, 20 two-rupee coins, and 10 five-rupee coins. If one coin is chosen at random, find the probability that the coin
(i) is a 50-paise coin.
(ii) will not be a 5-rupee coin.
🟢 Answer:
Total=100+50+20+10=180.
• (i) P(50p)=100/180=5/9.
• (ii) P(not 5₹)=1–10/180=1–1/18=17/18.
🔵 Question 11: Gopi buys a fish for his aquarium. The shopkeeper takes one fish at random from a tank containing 5 male fish and 8 female fish. What is the probability that the fish taken out is a male fish?
🟢 Answer:
• Total fish = 5 + 8 = 13
• Favourable outcomes (male) = 5
➡️ ✔️ P(male) = 5 / 13
🔵 Question 12: A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1–8 (see Fig. 14.5), and these are equally likely outcomes. What is the probability that it will point at
(i) 8 (ii) an odd number (iii) a number greater than 2 (iv) a number less than 9?
🟢 Answer:
• Sample space S = {1,2,3,4,5,6,7,8}, n(S)=8
(i) Favourable outcomes={8}, n(E)=1
➡️ ✔️ P=1/8
(ii) Odd numbers={1,3,5,7}, n(E)=4
➡️ ✔️ P=4/8=1/2
(iii) Numbers>2={3,4,5,6,7,8}, n(E)=6
➡️ ✔️ P=6/8=3/4
(iv) Numbers<9={1,2,3,4,5,6,7,8}, n(E)=8
➡️ ✔️ P=8/8=1
🔵 Question 13: A die is thrown once. Find the probability of getting
(i) a prime number (ii) a number between 2 and 6 (iii) an odd number.
🟢 Answer:
• S={1,2,3,4,5,6}, n(S)=6
(i) Primes={2,3,5}, n(E)=3
➡️ ✔️ P=3/6=1/2
(ii) Numbers between 2 and 6={3,4,5}, n(E)=3
➡️ ✔️ P=3/6=1/2
(iii) Odd numbers={1,3,5}, n(E)=3
➡️ ✔️ P=3/6=1/2
🔵 Question 14: One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting
(i) a king of red colour (ii) a face card (iii) a red face card (iv) the jack of hearts.
🟢 Answer:
(i) Red kings=2 (♦K, ♥K)
➡️ ✔️ P=2/52=1/26
(ii) Face cards (J,Q,K) total=12
➡️ ✔️ P=12/52=3/13
(iii) Red face cards=6 (♦J,Q,K and ♥J,Q,K)
➡️ ✔️ P=6/52=3/26
(iv) Jack of hearts=1
➡️ ✔️ P=1/52
🔵 Question 15: Five cards—the ten, jack, queen, king and ace of diamonds—are well-shuffled with their face downwards. One card is picked at random. Find the probability of
(i) a king (ii) a queen or an ace.
🟢 Answer:
• S={10,J,Q,K,A}, n(S)=5
(i) Kings={K}, n(E)=1
➡️ ✔️ P=1/5
(ii) Queen or Ace={Q,A}, n(E)=2
➡️ ✔️ P=2/5
🔵 Question 16: A letter is picked at random from the English alphabet. Find the probability that it is
(i) a vowel (ii) a consonant.
🟢 Answer:
• Total letters=26
• Vowels={A,E,I,O,U}, n(E)=5
➡️ (i) ✔️ P(vowel)=5/26
➡️ (ii) ✔️ P(consonant)=21/26
🔵 Question 17: A lot of 20 bulbs contains 4 defective ones. One bulb is drawn at random. What is the probability that the bulb drawn is
(i) defective (ii) not defective?
🟢 Answer:
• Total=20
(i) Defective=4
➡️ ✔️ P(defective)=4/20=1/5
(ii) Not defective=20–4=16
➡️ ✔️ P(not defective)=16/20=4/5
🔵 Question 18: A box contains 90 discs numbered 1–90. One disc is drawn at random. Find the probability that it bears
(i) a two-digit number (ii) a perfect square number (iii) a number divisible by 5.
🟢 Answer:
• Total numbers=90
(i) Two-digit numbers=10–90 ⇒81
➡️ ✔️ P=81/90=9/10
(ii) Perfect squares ≤90: 1,4,9,16,25,36,49,64,81 ⇒9 numbers
➡️ ✔️ P=9/90=1/10
(iii) Multiples of 5 ≤90: 5,10,…,90 ⇒18 numbers
➡️ ✔️ P=18/90=1/5
🔵 Question 19: A child has a die whose six faces show the letters as given below: [A] [B] [C] [D] [E] [A]. The die is thrown once. What is the probability of getting (i) A? (ii) D?
🟢 Answer:
🔹 Step 1: Total outcomes = 6
🔹 Step 2: Count(A) = 2 and Count(D) = 1
🔹 Step 3 (i): P(A) = 2/6 = 1/3 ✔️
🔹 Step 4 (ii): P(D) = 1/6 ✔️
🔵 Question 20: Suppose you drop a die at random on the rectangular region shown in Fig. 14.6. What is the probability that it will land inside the circle with diameter 1 m?
🟢 Answer:
🔹 Step 1: Area of rectangle, Aᵣₑcₜ = 3 m × 2 m = 6 m²
🔹 Step 2: Radius of circle, r = (diameter)/2 = 1/2 = 0.5 m
🔹 Step 3: Area of circle, A_cᵢᵣ = π r² = π × (0.5)² = π/4 m²
🔹 Step 4: Required probability = A_cᵢᵣ / Aᵣₑcₜ = (π/4) / 6 = π/24 ✔️
🔵 Question 21: A lot consists of 144 ball pens of which 20 are defective and the others are good. Nuri will buy a pen if it is good, but will not buy if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that (i) she will buy it? (ii) she will not buy it?
🟢 Answer:
🔹 Step 1: Total pens = 144
🔹 Step 2: Good pens = 144 − 20 = 124; Defective pens = 20
🔹 Step 3 (i): P(buy) = 124/144 = 31/36 ✔️
🔹 Step 4 (ii): P(not buy) = 20/144 = 5/36 ✔️
🔵 Question 22: Refer to Example 13. (i) Complete the following table of probabilities for “Sum on 2 dice” (2 to 12). (ii) A student argues that “there are 11 possible sums (2–12). Therefore, each has probability 1/11.” Do you agree? Justify your answer.
🟢 Answer:
🔹 Step 1: Total ordered outcomes when 2 dice are thrown = 6² = 36
🔹 Step 2: Count outcomes for each sum s (2→12):
• s=2 → 1 outcome → 1/36
• s=3 → 2 outcomes → 2/36 = 1/18
• s=4 → 3 outcomes → 3/36 = 1/12
• s=5 → 4 outcomes → 4/36 = 1/9
• s=6 → 5 outcomes → 5/36
• s=7 → 6 outcomes → 6/36 = 1/6
• s=8 → 5 outcomes → 5/36
• s=9 → 4 outcomes → 4/36 = 1/9
• s=10 → 3 outcomes → 3/36 = 1/12
• s=11 → 2 outcomes → 2/36 = 1/18
• s=12 → 1 outcome → 1/36
🔹 Step 3 (i): Table completed as above ✔️
🔹 Step 4 (ii): Disagree—sums are not equally likely because counts differ (e.g., 7 has 6 outcomes; 2 has 1) ✔️
🔵 Question 23: A game consists of tossing a one-rupee coin 3 times and noting its outcome each time. Hanif wins if all the tosses give the same result, i.e., three heads or three tails, and loses otherwise. Calculate the probability that Hanif will lose the game.
🟢 Answer:
🔹 Step 1: Total outcomes = 2³ = 8
🔹 Step 2: Winning outcomes = {HHH, TTT} = 2
🔹 Step 3: Losing outcomes = 8 − 2 = 6
🔹 Step 4: P(lose) = 6/8 = 3/4 ✔️
🔵 Question 24: A die is thrown twice. What is the probability that (i) 5 will not come up either time? (ii) 5 will come up at least once?
🟢 Answer:
🔹 Step 1: For one throw, P(not 5) = 5/6
🔹 Step 2 (i): Independent throws ⇒ P(no 5 in two throws) = (5/6)² = 25/36 ✔️
🔹 Step 3 (ii): P(at least one 5) = 1 − (5/6)² = 1 − 25/36 = 11/36 ✔️
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS FOR EXAMS
🧾🔵 Section A (1 mark each)
🔹 Q1. A fair die is rolled once. Find the probability of getting 3.
🟢 Answer:
1️⃣ Total outcomes = 6
2️⃣ Favourable outcomes = {3} = 1
3️⃣ ✔️ P(3) = 1/6
🔹 Q2. What is P(getting a head) when a coin is tossed?
🟢 Answer:
1️⃣ Sample space S = {H,T} → n(S)=2
2️⃣ Favourable = {H}=1
3️⃣ ✔️ P(H)=1/2
🔹 Q3. A bag has 5 red and 7 blue balls. Find P(red).
🟢 Answer:
1️⃣ Total = 5+7=12
2️⃣ Favourable(red)=5
3️⃣ ✔️ P=5/12
🔹 Q4. Probability of an impossible event is ___.
🟢 Answer: ✔️ 0
🔹 Q5. Fill: P(E)+P(E′)= ___.
🟢 Answer: ✔️ 1
🔹 Q6. Write the range of probability values.
🟢 Answer: ✔️ 0 ≤ P(E) ≤ 1
🔵 Section B (2 marks each)
🔹 Q7. A card is drawn from a pack of 52. Find P(face card).
🟢 Answer:
1️⃣ Face cards = 12 (J,Q,K of each suit)
2️⃣ Total cards = 52
3️⃣ ✔️ P=12/52=3/13
🔹 Q8. Two dice are thrown. Find P(sum=7).
🟢 Answer:
1️⃣ Total outcomes = 6×6 = 36
2️⃣ Favourable pairs = (1,6),(2,5),(3,4),(4,3),(5,2),(6,1)=6
3️⃣ ✔️ P=6/36=1/6
🔹 Q9. A bag has 4 white, 5 black, 3 red balls. A ball is drawn. Find P(black or red).
🟢 Answer:
1️⃣ Total = 4+5+3=12
2️⃣ Favourable = 5+3=8
3️⃣ ✔️ P=8/12=2/3
🔹 Q10. In a lottery of 1000 tickets numbered 1–1000, one ticket is drawn. Find P(getting a number divisible by 5).
🟢 Answer:
1️⃣ Multiples of 5 from 1–1000 = 1000/5 = 200
2️⃣ ✔️ P=200/1000=1/5
🔹 Q11. A spinner numbered 1–8 is spun. Find P(getting an even number).
🟢 Answer:
1️⃣ Even numbers={2,4,6,8}=4
2️⃣ Total=8
3️⃣ ✔️ P=4/8=1/2
🔹 Q12. A coin is tossed 3 times. Find P(all heads).
🟢 Answer:
1️⃣ Total outcomes=2³=8
2️⃣ Favourable={HHH}=1
3️⃣ ✔️ P=1/8
🔵 Q13. Two dice are rolled. Find P(sum = 10).
🟢 Answer:
1️⃣ Total outcomes = 6² = 36
2️⃣ Favourable pairs for sum 10: (4,6),(5,5),(6,4) → 3
3️⃣ ✔️ P = 3 / 36 = 1 / 12
🔵 Q14. A card is drawn from 52 cards. Find P(getting)
(i) red king (ii) king or queen (iii) not a face card.
🟢 Answer:
1️⃣ (i) Red kings = 2 ⇒ P = 2/52 = 1/26
2️⃣ (ii) Kings(4)+Queens(4)=8 ⇒ P = 8/52 = 2/13
3️⃣ (iii) Face cards=12 ⇒ Non-face=52−12=40 ⇒ P = 40/52=10/13 ✔️
🔵 Q15. A bag has 3 red, 5 blue, 2 green balls. Two balls are drawn together. Find P(both blue).
🟢 Answer:
1️⃣ Total ways = C₁₀² = 10C2 = 45
2️⃣ Favourable (blue) = C₅² = 5C2 = 10
3️⃣ ✔️ P = 10/45 = 2/9
🔵 Q16. A coin is tossed 4 times. Find P(exactly 3 heads).
🟢 Answer:
1️⃣ Total outcomes = 2⁴ = 16
2️⃣ Favourable = C₄³ = 4
3️⃣ ✔️ P = 4/16 = 1/4
🔵 Q17. A card is drawn. Find P(it is neither king nor ace).
🟢 Answer:
1️⃣ Kings=4, Aces=4 ⇒ Total unfavourable=8
2️⃣ Remaining=52−8=44
3️⃣ ✔️ P = 44/52 = 11/13
🔵 Q18. A die is thrown twice. Find P(getting at least one six).
🟢 Answer:
1️⃣ P(no six in one throw)=5/6
2️⃣ P(no six in two throws)=(5/6)²=25/36
3️⃣ ✔️ P(at least one six)=1−25/36=11/36
🔵 Q19. From numbers 1–90, one is chosen. Find P(perfect square or divisible by 10).
🟢 Answer:
1️⃣ Perfect squares ≤90: {1,4,9,16,25,36,49,64,81} → 9
2️⃣ Multiples of 10 ≤90: {10,20,…,90} → 9
3️⃣ Common elements: {… none …} →0
4️⃣ Total favourable=9+9=18
5️⃣ ✔️ P=18/90=1/5
🔵 Q20. A bag contains 4 red, 6 green, 5 blue balls. A ball is drawn, colour noted, then replaced. Another ball is drawn. Find P(both green).
🟢 Answer:
1️⃣ P(green)=6/(4+6+5)=6/15=2/5
2️⃣ Events independent ⇒ P(both)= (2/5)²=4/25 ✔️
🔵 Q21. Internal Choice:
(A) Three unbiased coins are tossed. Find P(getting at least two heads).
OR
(B) Two dice are rolled. Find P(getting different numbers on both dice).
🟢 Answer A:
1️⃣ Total outcomes=2³=8
2️⃣ At least two heads ⇒ {HHT,HTH,THH,HHH}=4
3️⃣ ✔️ P=4/8=1/2
🟢 Answer B:
1️⃣ Total outcomes=36
2️⃣ Same numbers=6 ⇒ Different=36−6=30
3️⃣ ✔️ P=30/36=5/6
🔵 Q22. Internal Choice:
(A) From a pack of cards, find P(getting a red card or a black king).
OR
(B) A die is thrown thrice. Find P(getting exactly two fours).
🟢 Answer A:
1️⃣ Red cards=26, Black kings=2 ⇒ Overlap none
2️⃣ ✔️ P=28/52=7/13
🟢 Answer B:
1️⃣ Total outcomes=6³=216
2️⃣ Choose positions for two fours=C₃²=3
3️⃣ Probability of four=(1/6)²; non-four=(5/6)
4️⃣ ✔️ P=3×(1/6)²×(5/6)=15/216=5/72
🔵 Q23. A bag contains 6 red, 5 blue and 4 green balls. Two balls are drawn one after another without replacement. Find the probability that
(i) both are red (ii) first is red and second is blue.
🟢 Answer:
1️⃣ Total balls = 6 + 5 + 4 = 15
2️⃣ (i) First red P₁ = 6/15, Second red P₂ = 5/14
➡️ ✔️ P(both red) = (6/15) × (5/14) = 30/210 = 1/7
3️⃣ (ii) First red = 6/15, then blue = 5/14
➡️ ✔️ P = (6/15) × (5/14) = 30/210 = 1/7
🔵 Q24. A box has 100 bulbs of which 10 are defective. Two bulbs are selected at random with replacement. Find the probability that
(i) none are defective (ii) at least one is defective.
🟢 Answer:
1️⃣ P(defective) = 10/100 = 1/10
2️⃣ P(not defective) = 9/10
3️⃣ (i) None defective = (9/10)² = 81/100 ✔️
4️⃣ (ii) At least one defective = 1 − (9/10)² = 1 − 81/100 = 19/100 ✔️
🔵 Q25. A card is drawn from a well-shuffled deck and replaced. This is repeated 3 times. Find the probability of getting exactly two kings.
🟢 Answer:
1️⃣ Total trials n = 3, Success (king) probability p = 4/52 = 1/13
2️⃣ Use binomial: P(X=2) = C₃² (p)² (1−p)
3️⃣ C₃² = 3, p = 1/13, (1−p)=12/13
➡️ ✔️ P = 3 × (1/13)² × (12/13) = (36)/(2197)
🔵 Q26. Internal Choice:
(A) Two different dice are rolled together. Find P(the sum is divisible by 3).
OR
(B) Three coins are tossed. Find P(getting more tails than heads).
🟢 Answer A:
1️⃣ Total outcomes = 6² = 36
2️⃣ Sum divisible by 3: possible sums = {3,6,9,12}
• Sum=3 →2 outcomes
• Sum=6 →5 outcomes
• Sum=9 →4 outcomes
• Sum=12→1 outcome
✔️ Total favourable =2+5+4+1=12
3️⃣ ✔️ P=12/36=1/3
🟢 Answer B:
1️⃣ Outcomes for three coins = 2³=8
2️⃣ More tails than heads ⇒ {TTT,TTH,THT,HTT}=4
3️⃣ ✔️ P=4/8=1/2
🔵 Q27. A die is thrown twice. Find P(the product of the two numbers is even and divisible by 3).
🟢 Answer:
1️⃣ Total outcomes =36
2️⃣ Even & divisible by 3 ⇒ product divisible by 6.
3️⃣ Count pairs (a,b) where product divisible by 6:
• Multiples of 6 occur for (2,3),(3,2),(3,4),(4,3),(3,6),(6,3),(2,6),(6,2),(6,6),(4,6),(6,4),(5,6),(6,5)… (list systematically) =12
4️⃣ ✔️ P=12/36=1/3
🔵 Q28. A card is drawn from a pack. Find P(it is)
(i) a black face card (ii) neither an ace nor a king nor a queen nor a jack.
🟢 Answer:
1️⃣ (i) Black face cards = J,Q,K of ♠ and ♣ =6
➡️ ✔️ P=6/52=3/26
2️⃣ (ii) Aces(4)+Kings(4)+Queens(4)+Jacks(4)=16
Remaining=52−16=36
➡️ ✔️ P=36/52=9/13
🔵 Q29. A bag has 8 red, 7 blue and 5 green balls. Two balls are drawn without replacement. Find P(both balls of different colours).
🟢 Answer:
1️⃣ Total balls=20
2️⃣ Total ways=C₂₀²=190
3️⃣ Same colour combos:
• Red: C₈²=28
• Blue: C₇²=21
• Green: C₅²=10
Total same=59
4️⃣ Different colours=190−59=131
➡️ ✔️ P=131/190
🔵 Q30. Internal Choice:
(A) A box contains 5 defective and 95 non-defective bulbs. Two bulbs are drawn without replacement. Find P(at least one defective).
OR
(B) A coin is tossed 5 times. Find P(exactly 3 heads).
🟢 Answer A:
1️⃣ Total bulbs=100
2️⃣ P(no defective)=C₉₅²/C₁₀₀²
• C₉₅²=4465
• C₁₀₀²=4950
P=4465/4950
3️⃣ ✔️ P(at least one defective)=1−4465/4950=485/4950=97/990
🟢 Answer B:
1️⃣ Use binomial: P(X=3)=C₅³(1/2)³(1/2)²=C₅³/32=10/32=5/16 ✔️
———————————————————————————————————————————————————————————————————————————–
MIND MAP