Class 10 : Maths (In English) – Lesson 12. Surface Areas and Volumes

EXPLANATION & SUMMARY

🔵 Introduction and Real-World Context
Surface area and volume calculations let us design tanks, paint curved walls, make packaging, or recast metals. Class 10 builds on Class 9 by:
• 🟢 Extending TSA/CSA/Volume of cube, cuboid, cylinder, cone, sphere, hemisphere.
• 🟡 Applying them to composite shapes, hollow solids, melting & recasting.
• 🔴 Introducing the frustum of a cone for truncated cones, buckets, lampshades.
💡 Concept: Surface area measures boundary exposure (paint, polish). Volume measures 3-D capacity (liquid, metal quantity).

📌 1. Cube and Cuboid Refresher
🔵 Cube (side a):
• TSA = 6 a²
• LSA (CSA) = 4 a²
• V = a³
🟢 Cuboid (l × b × h):
• TSA = 2(lb + bh + lh)
• LSA = 2 h(l + b)
• V = l × b × h
✏️ Note: For open-top boxes, exclude the top face in TSA.

📌 2. Right Circular Cylinder
🟡 Definitions: r = radius, h = height.
• CSA = 2 π r h (only curved side).
• TSA = 2 π r(h + r) (curved + two circular ends).
• V = π r² h.
🌿 Example Application: Finding the metal sheet for a closed water tank: use TSA.
✔ Check: Units → CSA/TSA in cm² or m², Volume in cm³ or m³.

📌 3. Right Circular Cone
🔵 Cone parameters: r = radius, h = height, l = slant height.
• l = √(r² + h²).
• CSA = π r l.
• TSA = π r(l + r).
• V = (1/3) π r² h.
💡 Concept: A traffic cone or temple shikhara approximates a cone.
✏️ Note: When two cones join base-to-base, common base circle is not exposed in TSA.

📌 4. Sphere and Hemisphere
🟢 Sphere (radius r):
• Surface Area = 4 π r².
• V = (4/3) π r³.
🟡 Hemisphere (radius r):
• CSA = 2 π r² (curved half).
• TSA = 3 π r² (curved + base).
• V = (2/3) π r³.
🔴 Real-life: Balls, planets, bubbles, domes.

📌 5. Hollow Cylinder (Pipe)
🔵 Outer radius R, inner radius r, height h.
• Material Volume = π(R² − r²) h.
• Outer CSA = 2 π R h.
• Inner CSA = 2 π r h.
• Rim areas (two annuli) = 2 π(R² − r²).
🌿 Use in chimneys or metal pipes.

📌 6. Composite Solids
⚡ Approach: Break into basic solids, calculate each, then add or subtract.
🟢 Ice-cream Cone Example: Hemisphere on cone.
 V₍total₎ = (2/3) π r³ + (1/3) π r² h.
 TSA_exposed = π r l + 2 π r² (exclude common circle).
🟡 Temple Structure: Cone on cylinder.
 V₍total₎ = π r² h_cyl + (1/3) π r² h_cone.
🔴 Drilled Block: Block volume − Cylinder hole volume.
✔ Tip: Always draw a quick sketch marking hidden/exposed parts.

📌 7. Melting and Recasting (Volume Conservation)
🔵 Principle: Mass conserved ⇒ density constant ⇒ V₍initial₎ = V₍final₎.
🟢 Example: A big sphere melted into small spheres.
 (4/3) π R³ = n × (4/3) π r³ ⇒ n = (R³ ÷ r³).
🟡 Example: A cylinder recast into wires.
 π R² H = n × π r_w² L ⇒ n = (R² H) ÷ (r_w² L).
✏️ Note: Convert volumes to litres: 1 m³ = 1000 L.

📌 8. Frustum of a Cone
🌟 Definition: A truncated cone formed by slicing a larger cone parallel to its base.
🔵 Parameters: R (big base), r (small base), h (height), l (slant height).
• l = √((R − r)² + h²).
• CSA = π(R + r) l.
• TSA = CSA + π R² + π r².
• V = (1/3) π h(R² + r² + R r).
💡 Concept: Buckets, lampshades, and flowerpots are frustums.
✏️ Note: If l given, compute h = √(l² − (R − r)²) when required.

📌 9. Real-World Applications
🟢 Painting/Polishing: Use TSA (or CSA if open). Example: paint on a silo.
🟡 Cost of Sheet Metal: Use TSA to find required area × cost rate.
🔵 Capacity: Use volume to find litres of water a tank can hold.
🔴 Engineering: Designing domes, spires, or wheels uses these formulas.
✔ Double-check units: m² for area, m³ for volume.

📌 10. Board-Style Problem Approaches
⚡ Strategy Steps:
🔵 Step 1: Write Given values (with units).
🟢 Step 2: Identify required quantity (TSA, CSA, V).
🟡 Step 3: Choose formula → Substitute → Simplify.
🔴 Step 4: Box or bold final answer with units.
💡 Example Thought: “How much paint for a cylindrical tank open at top?” → TSA = CSA + base area only = 2 π r h + π r².

📌 11. Scaling Laws
🟢 Linear scale factor k → Surface Area scales k², Volume scales k³.
✏️ Note: This appears in tricky application problems.

📌 12. Common Errors & Fixes
🔵 Mixing units (cm, m, L) → Convert before computing.
🟢 Adding hidden areas at junctions → Only count exposed surfaces.
🟡 Confusing h and l in cones/frustums → Recompute: l = √(r² + h²) or l = √((R − r)² + h²).
🔴 Using π incorrectly (22/7 vs 3.14) mid-calculation → Stay consistent.

📌 13. Further Worked Examples (Concept Flows)
🧠 Example A – Hemisphere Bowl: Find paint area (CSA only).
🧠 Example B – Hollow Pipe: Find metal volume: π(R² − r²) h.
🧠 Example C – Recasting Metal: V₍initial₎ = V₍final₎ → find number of new shapes.
🧠 Example D – Bucket (Frustum): Use frustum volume formula; convert to litres.

📌 14. Connections to Other Topics
🔵 Mensuration (Class 9): Builds directly on previous formulas.
🟢 Trigonometry: Sometimes needed to find heights/slant heights.
🟡 Statistics/Probability: Cylindrical containers in word problems.
🔴 Real-life Geometry: Architecture, manufacturing, civil engineering.

📌 15. Best Practices for Board Exams
🟢 Always sketch shapes for clarity.
🔵 Write formula before substitution to earn method marks.
🟡 Keep π symbolic unless asked for decimal.
🔴 Highlight final answer.
✔ Use V₍final₎ notation for volume after recasting steps.

📌 16. Comprehensive Formula Capsule
• Cylinder: CSA = 2 π r h, TSA = 2 π r(h + r), V = π r² h.
• Cone: l = √(r² + h²), CSA = π r l, TSA = π r(l + r), V = (1/3) π r² h.
• Sphere: SA = 4 π r², V = (4/3) π r³.
• Hemisphere: CSA = 2 π r², TSA = 3 π r², V = (2/3) π r³.
• Frustum: l = √((R − r)² + h²), CSA = π(R + r) l, TSA = CSA + π(R² + r²), V = (1/3) π h(R² + r² + R r).
• Hollow Cylinder: V = π(R² − r²) h.

📌 17. Reasoning Patterns Without Numbers
🔵 “Paint outside of hemispherical bowl?” → CSA of hemisphere.
🟢 “Find number of spheres from melted cylinder?” → V₍initial₎ ÷ V₍sphere₎.
🟡 “Find sheet for closed cone + hemisphere?” → Sum exposed surfaces only.
🔴 “Frustum bucket capacity?” → Frustum volume; convert to litres.

📌 18. Exam Question Signals
🌿 Keywords → Action:
• “Curved surface area” → CSA only.
• “Total surface area” → Include ends/bases.
• “Open at top” → Exclude top base.
• “Recast/melted” → Use V₍initial₎ = V₍final₎.
• “Bucket” → Frustum formula.

📌 19. Unit Conversion Reminders
• 1 m² = 10⁴ cm².
• 1 m³ = 10⁶ cm³ = 1000 L.
• 1 cm³ = 1 mL.
✏️ Note: Always convert before substitution.

📌 20. Final Practice Advice
🔵 Start with simpler shapes to warm up.
🟢 Progress to mixed/real-life problems.
🟡 Check each step and units.
🔴 Use clean diagrams and highlight final answers.

:
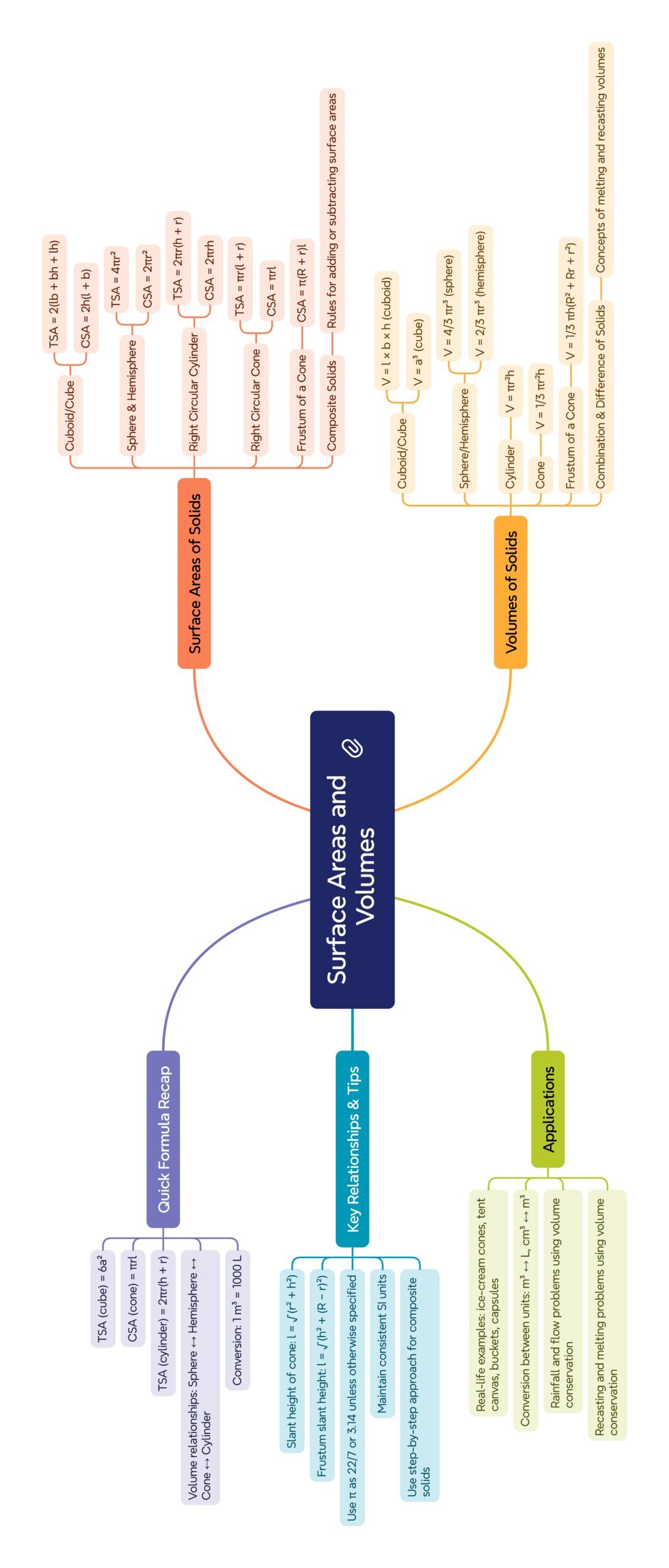
🌈 Surface Areas and Volumes — Summary (~300 words)
🔵 Core Principles
• Surface Area measures exposed boundary; Volume measures 3-D capacity.
• Always write Formula → Substitution → Simplification → Final answer (with unit).
• Units: Area in cm²/m², Volume in cm³/m³; convert to litres (1 m³ = 1000 L) if needed.
🟢 Base Solids
• Cube (a): TSA = 6a², LSA = 4a², V = a³.
• Cuboid (l, b, h): TSA = 2(lb + bh + lh), LSA = 2h(l + b), V = l × b × h.
• Cylinder (r, h): CSA = 2πrh, TSA = 2πr(h + r), V = πr²h.
• Cone (r, h): l = √(r² + h²), CSA = πrl, TSA = πr(l + r), V = (1/3)πr²h.
• Sphere (r): SA = 4πr², V = (4/3)πr³.
• Hemisphere (r): CSA = 2πr², TSA = 3πr², V = (2/3)πr³.
🟡 Frustum of a Cone (R, r, h):
• l = √((R − r)² + h²).
• CSA = π(R + r)l.
• TSA = CSA + π(R² + r²).
• V = (1/3)πh(R² + r² + Rr).
🔴 Composite Solids
• Add or subtract volumes and exposed surfaces for combinations (e.g., cone + hemisphere).
• Hollow Cylinder (R, r, h): V = π(R² − r²)h.
🌿 Melting and Recasting
• Use V₍initial₎ = V₍final₎ for same material; number of objects = V₍initial₎ ÷ V₍one piece₎.
⚡ Applications & Tips
• Painting/polishing = TSA × cost rate.
• Capacity problems = Volume → litres.
• Keep π symbolic unless instructed to use 22/7 or 3.14.
• Exclude hidden junction areas in TSA.
• Sketch shapes, mark exposed surfaces, and check units at every step.
Outcome: Mastering these ensures accurate, efficient solutions for NCERT and board-style questions.

📝 Quick Recap
🔵 TSA vs CSA: Include only exposed surfaces.
🟢 Frustum: l = √((R − r)² + h²); V = (1/3)πh(R² + r² + Rr).
🟡 Volume conserved in melting/recasting: V₍initial₎ = V₍final₎.
🔴 Pipes: V = π(R² − r²)h.
✔ Always: Formula → Substitution → Simplification → Final answer (with unit).

———————————————————————————————————————————————————————————————————————————–

TEXT BOOK QUESTIONS

Exercise 12.1

🔵 Question
Q 1. 2 cubes each of volume 64 cm³ are joined end to end. Find the surface area of the resulting cuboid.
🟢 Answer
💡 Concept: Two identical cubes (side = a) joined face-to-face form a cuboid of size (2a) × a × a.
🔵 Step 1: Given a³ = 64 cm³.
🔵 Step 2: a = ³√64 = 4 cm.
🔵 Step 3: Cuboid dimensions = 8 cm × 4 cm × 4 cm.
🔵 Step 4: TSA(cuboid) = 2(lw + lh + wh).
🔵 Step 5: = 2(8×4 + 8×4 + 4×4).
🔵 Step 6: = 2(32 + 32 + 16).
🔵 Step 7: = 2×80 = 160 cm².
✔️ Final: 160 cm².
✏️ Note: The common face becomes internal; using the cuboid TSA directly is valid.

🔵 Question
Q 2. A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.
🟢 Answer
💡 Concept: Inner surface = CSA(hemisphere) + CSA(cylinder) = 2πr² + 2πrh.
🔵 Step 1: Diameter = 14 cm ⇒ r = 7 cm.
🔵 Step 2: Total height = 13 cm ⇒ cylinder height h = 13 − r = 6 cm.
🔵 Step 3: CSA(hemisphere) = 2πr² = 2×(22/7)×7² = 308 cm².
🔵 Step 4: CSA(cylinder) = 2πrh = 2×(22/7)×7×6 = 264 cm².
🔵 Step 5: Inner surface area = 308 + 264 = 572 cm².
✔️ Final: 572 cm².

🔵 Question
Q 3. A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
🟢 Answer
💡 Concept: Bases are hidden; TSA = πrl + 2πr².
🔵 Step 1: r = 3.5 cm.
🔵 Step 2: Cone height h = 15.5 − 3.5 = 12 cm.
🔵 Step 3: Slant height l = √(r² + h²) = √(3.5² + 12²) = √(12.25 + 144) = √156.25 = 12.5 cm.
🔵 Step 4: CSA(cone) = πrl = (22/7)×3.5×12.5 = 137.5 cm².
🔵 Step 5: CSA(hemisphere) = 2πr² = 2×(22/7)×(3.5)² = 77 cm².
🔵 Step 6: TSA = 137.5 + 77 = 214.5 cm².
✔️ Final: 214.5 cm².

🔵 Question
Q 4. A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
🟢 Answer
💡 Concept: Greatest hemisphere fits exactly on the top face ⇒ diameter = side of cube; exposed area = 5 faces of cube + (uncovered part of top face) + CSA(hemisphere).
🔵 Step 1: Side a = 7 cm ⇒ greatest diameter = 7 cm ⇒ r = 3.5 cm.
🔵 Step 2: Area of 5 faces of cube = 5a² = 5×7² = 245 cm².
🔵 Step 3: Uncovered part of top face = a² − πr² = 49 − (22/7)×(3.5)² = 49 − 38.5 = 10.5 cm².
🔵 Step 4: CSA(hemisphere) = 2πr² = 2×(22/7)×(3.5)² = 77 cm².
🔵 Step 5: Total surface area = 245 + 10.5 + 77 = 332.5 cm².
✔️ Final: 332.5 cm².
🔴 Common mistake: Adding 5a² + 2πr² only (misses the uncovered ring on the top face).

🔵 Question
Q 5. A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
🟢 Answer
💡 Concept: New surface = SA(cube) − area of removed circle + CSA(hemispherical cavity).
🔵 Step 1: Let edge of cube = a; then r = a/2.
🔵 Step 2: SA(cube) = 6a².
🔵 Step 3: Area of removed circle = πr² = π(a/2)² = (πa²)/4.
🔵 Step 4: CSA(hemisphere cavity) = 2πr² = 2π(a/2)² = (πa²)/2.
🔵 Step 5: Required SA = 6a² − (πa²)/4 + (πa²)/2.
🔵 Step 6: = 6a² + (πa²)/4 = (6 + π/4)a².
✔️ Final: (6 + π/4)a² cm².
✏️ Note: One face now has a circular hole; its flat circular area is removed and replaced by the curved hemispherical cavity.

🔵 Question
Q 6. A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see Fig. 12.10). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.
🟢 Answer
💡 Concept: TSA = CSA(cylinder) + CSA(two hemispheres) = 2πrh + 4πr².
🔵 Step 1: Diameter = 5 mm ⇒ r = 2.5 mm.
🔵 Step 2: Cylindrical height h = total length − 2r = 14 − 5 = 9 mm.
🔵 Step 3: 2πrh = 2×(22/7)×2.5×9 = 990/7 mm².
🔵 Step 4: 4πr² = 4×(22/7)×(2.5)² = 550/7 mm².
🔵 Step 5: TSA = (990/7 + 550/7) = 1540/7 = 220 mm².
✔️ Final: 220 mm².

🔵 Question
Q 7. A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of ₹500 per m². (Note that the base of the tent will not be covered with canvas.)
🟢 Answer
💡 Concept: Canvas area = CSA(cylinder) + CSA(cone). Base is open.
🔵 Step 1: r = 4/2 = 2 m, h = 2.1 m, l = 2.8 m.
🔵 Step 2: CSA(cylinder) = 2πrh = 2×π×2×2.1 = 8.4π = 26.4 m² (π = 22/7).
🔵 Step 3: CSA(cone) = πrl = π×2×2.8 = 5.6π = 17.6 m².
🔵 Step 4: Total canvas area = 26.4 + 17.6 = 44 m².
🔵 Step 5: Cost = 44 × 500 = ₹22,000.
✔️ Final: Canvas area = 44 m²; Cost = ₹22,000.

🔵 Question
Q 8. From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm².
🟢 Answer
💡 Concept: Exposed area = CSA(cylinder) + CSA(cone cavity) + area of the base circle (the top circle is removed by the cavity).
🔵 Step 1: r = 1.4/2 = 0.7 cm, h = 2.4 cm.
🔵 Step 2: Slant height l = √(r² + h²) = √(0.7² + 2.4²) = √(0.49 + 5.76) = √6.25 = 2.5 cm.
🔵 Step 3: CSA(cylinder) = 2πrh = 2×(22/7)×0.7×2.4 = 10.56 cm².
🔵 Step 4: CSA(cone cavity) = πrl = (22/7)×0.7×2.5 = 5.5 cm².
🔵 Step 5: Base circle area = πr² = (22/7)×(0.7)² = 1.54 cm².
🔵 Step 6: TSA(remaining) = 10.56 + 5.5 + 1.54 = 17.6 cm².
✔️ Final: 18 cm² (nearest cm²).

🔵 Question
Q 9. A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. 12.11. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
🟢 Answer
💡 Concept: Exposed area = CSA(cylinder) + CSA(two hemispherical cavities) = 2πrh + 4πr².
🔵 Step 1: r = 3.5 cm, h = 10 cm.
🔵 Step 2: CSA(cylinder) = 2πrh = 2×(22/7)×3.5×10 = 220 cm².
🔵 Step 3: CSA(two hemispheres) = 4πr² = 4×(22/7)×(3.5)² = 154 cm².
🔵 Step 4: Total surface area = 220 + 154 = 374 cm².
✔️ Final: 374 cm².

Exercise 12.2

🔵 Question
Q 1. A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
🟢 Answer
💡 Concept: Volume = V₍cone₎ + V₍hemisphere₎.
🔵 Step 1: r = 1 cm, h = r = 1 cm.
🔵 Step 2: V₍cone₎ = (1/3)πr²h = (1/3)π×1²×1 = π/3 cm³.
🔵 Step 3: V₍hemisphere₎ = (2/3)πr³ = (2/3)π×1³ = 2π/3 cm³.
🔵 Step 4: Total V = π/3 + 2π/3 = π cm³.
✔️ Final: π cm³.

🔵 Question
Q 2. Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)
🟢 Answer
💡 Concept: Volume = V₍cylinder₎ + 2×V₍cone₎.
🔵 Step 1: Diameter = 3 cm ⇒ r = 1.5 cm.
🔵 Step 2: Total length = 12 cm ⇒ cylinder height = 12 − 2×2 = 8 cm.
🔵 Step 3: V₍cylinder₎ = πr²h = π×(1.5)²×8 = π×2.25×8 = 18π cm³.
🔵 Step 4: V₍cone₎ = (1/3)πr²h = (1/3)π×(1.5)²×2 = (1/3)π×2.25×2 = 1.5π cm³.
🔵 Step 5: Volume of 2 cones = 2×1.5π = 3π cm³.
🔵 Step 6: Total volume = 18π + 3π = 21π cm³.
✔️ Final: 21π cm³.

🔵 Question
Q 3. A gulab jamun contains sugar syrup up to about 30 % of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm (see Fig. 12.15).
🟢 Answer
💡 Concept: One jamun volume = cylinder + sphere (two hemispheres). Syrup = 30 % of total.
🔵 Step 1: r = 2.8 ÷ 2 = 1.4 cm.
🔵 Step 2: Total length = 5 cm ⇒ cylindrical length = 5 − 2×1.4 = 2.2 cm.
🔵 Step 3: V₍cylinder₎ = πr²h = π×(1.4)²×2.2 = π×1.96×2.2 = 4.312π cm³.
🔵 Step 4: Volume of sphere = (4/3)πr³ = (4/3)π×(1.4)³ = (4/3)π×2.744 = 3.659π cm³.
🔵 Step 5: Total V per jamun = 4.312π + 3.659π = 7.971π cm³.
🔵 Step 6: Syrup per jamun = 0.30×7.971π = 2.3913π cm³.
🔵 Step 7: For 45 jamuns: Volume = 45×2.3913π ≈ 107.6π cm³.
🔵 Step 8: Using π = 22/7, syrup ≈ 107.6×3.142 ≈ 338 cm³.
✔️ Final: ≈ 338 cm³ syrup.

🔵 Question
Q 4. A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm × 10 cm × 3.5 cm. The radius of each depression is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see Fig. 12.16).
🟢 Answer
💡 Concept: Volume = V₍cuboid₎ − 4×V₍cone₎.
🔵 Step 1: V₍cuboid₎ = l×b×h = 15×10×3.5 = 525 cm³.
🔵 Step 2: V₍cone₎ = (1/3)πr²h = (1/3)π×(0.5)²×1.4 = (1/3)π×0.25×1.4 = (1/3)π×0.35 = 0.1167π cm³.
🔵 Step 3: Volume of 4 cones = 4×0.1167π = 0.4668π cm³ ≈ 1.466 cm³ (π=3.142).
🔵 Step 4: Remaining wood volume = 525 − 1.466 = 523.53 cm³.
✔️ Final: ≈ 523.5 cm³.

🔵 Question
Q 5. A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm, are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
🟢 Answer
💡 Concept: Volume displaced = (1/4)V₍cone₎ = N×V₍sphere₎.
🔵 Step 1: V₍cone₎ = (1/3)πr²h = (1/3)π×5²×8 = (1/3)π×25×8 = (200/3)π cm³.
🔵 Step 2: Water displaced = (1/4)×(200/3)π = (50/3)π cm³.
🔵 Step 3: V₍sphere₎ = (4/3)πr³ = (4/3)π×(0.5)³ = (4/3)π×0.125 = (0.5/3)π cm³ = (π/6) cm³.
🔵 Step 4: N×(π/6) = (50/3)π ⇒ N/6 = 50/3 ⇒ N = (50/3)×6 = 100.
✔️ Final: 100 lead shots.

🔵 Question
Q 6. A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm³ of iron ≈ 8 g.
🟢 Answer
💡 Concept: Mass = density × total volume.
🔵 Step 1: First cylinder radius r₁ = 24/2 = 12 cm, h₁ = 220 cm.
🔵 Step 2: V₁ = πr₁²h₁ = π×12²×220 = π×144×220 = 31 680π cm³.
🔵 Step 3: Second cylinder radius r₂ = 8 cm, h₂ = 60 cm.
🔵 Step 4: V₂ = πr₂²h₂ = π×64×60 = 3 840π cm³.
🔵 Step 5: Total volume = 31 680π + 3 840π = 35 520π cm³.
🔵 Step 6: Using π = 3.1416, volume ≈ 111 585 cm³.
🔵 Step 7: Mass = volume × 8 g = 111 585×8 = 892 680 g = 892.68 kg.
✔️ Final: ≈ 893 kg.

🔵 Question
Q 7. A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.
🟢 Answer
💡 Concept: V₍cylinder₎ − V₍cone+hemisphere₎ = remaining water.
🔵 Step 1: V₍cylinder₎ = πr²h = π×60²×180 = π×3 600×180 = 648 000π cm³.
🔵 Step 2: V₍cone₎ = (1/3)πr²h = (1/3)π×60²×120 = (1/3)π×3 600×120 = 144 000π cm³.
🔵 Step 3: V₍hemisphere₎ = (2/3)πr³ = (2/3)π×60³ = (2/3)π×216 000 = 144 000π cm³.
🔵 Step 4: Solid volume = 144 000π + 144 000π = 288 000π cm³.
🔵 Step 5: Water left = 648 000π − 288 000π = 360 000π cm³.
🔵 Step 6: Using π = 3.1416 ⇒ Volume ≈ 1 131 000 cm³ = 1.131 m³ = 1 131 L.
✔️ Final: ≈ 1 131 L of water.

🔵 Question
Q 8. A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds it to be 345 cm³. Check whether this is correct, taking the above as inside measurements, and π = 3.14.
🟢 Answer
💡 Concept: V₍vessel₎ = V₍sphere₎ + V₍cylinder₎.
🔵 Step 1: r₍cyl₎ = 2 ÷ 2 = 1 cm, h₍cyl₎ = 8 cm.
🔵 Step 2: r₍sphere₎ = 8.5 ÷ 2 = 4.25 cm.
🔵 Step 3: V₍cyl₎ = πr²h = 3.14×1²×8 = 25.12 cm³.
🔵 Step 4: V₍sphere₎ = (4/3)πr³ = (4/3)×3.14×(4.25³) = (4.1867)×76.77 = 321.38 cm³.
🔵 Step 5: Total V = 25.12 + 321.38 = 346.5 cm³.
🔵 Step 6: Child’s measurement = 345 cm³, which is ≈ 346.5 cm³, so it is correct.
✔️ Final: Yes, ≈ 346.5 cm³ confirms 345 cm³ is nearly correct.

————————————————————————————————————————————————————————————————————————————

OTHER IMPORTANT QUESTIONS FOR EXAMS

🔵 Section A — Very Short / Objective (Q1–Q6, 1 mark each)
🔵 Question 1
Find the total surface area of a cuboid of dimensions 4 cm × 3 cm × 2 cm.
🟢 Answer
➡️ Formula: TSA = 2(l×b + b×h + l×h)
➡️ Substitution: = 2(4×3 + 3×2 + 4×2)
➡️ Simplification: = 2(12 + 6 + 8) = 2×26 = 52 cm²
✔️ Final: 52 cm²

🔵 Question 2 (MCQ)
The volume of a sphere of radius 3 cm (take π = 22/7) is:
🟢 A. 100.57 cm³
🟡 B. 113.14 cm³
🔴 C. 118.80 cm³
🟠 D. 94.25 cm³
🧠 Answer: B
➡️ Working: V = (4/3)πr³ = (4/3)×(22/7)×3³ = 2376/21 ≈ 113.14 cm³

🔵 Question 3 (MCQ)
The curved surface area of a cylinder of radius 7 cm and height 10 cm is:
🟢 A. 220 cm²
🟡 B. 440 cm²
🔴 C. 308 cm²
🟠 D. 154 cm²
🧠 Answer: B
➡️ Working: CSA = 2πrh = 2×(22/7)×7×10 = 440 cm²

🔵 Question 4 (MCQ)
A cone has radius 9 cm and height 12 cm. Its slant height is:
🟢 A. 12 cm
🟡 B. 18 cm
🔴 C. 15 cm
🟠 D. 21 cm
🧠 Answer: C
➡️ Working: l = √(r² + h²) = √(9² + 12²) = √225 = 15 cm

🔵 Question 5 (MCQ)
The volume of a hemisphere of radius 2 cm equals:
🟢 A. 8π cm³
🟡 B. (16/3)π cm³
🔴 C. (4/3)π cm³
🟠 D. (32/3)π cm³
🧠 Answer: B
➡️ Working: V = (2/3)πr³ = (2/3)π×2³ = (16/3)π cm³

🔵 Question 6 (MCQ)
A cube has surface area 150 cm². Its edge length is:
🟢 A. 6 cm
🟡 B. 4 cm
🔴 C. 5 cm
🟠 D. 3 cm
🧠 Answer: C
➡️ Working: 6a² = 150 ⇒ a² = 25 ⇒ a = 5 cm

🟢 Section B — Short Answer-I (Q7–Q12, 2 marks each)
🔵 Question 7
Two cubes of volumes 27 cm³ and 8 cm³ are melted and recast into a cuboid of height 3 cm and breadth 3 cm. Find the length of the cuboid.
🟢 Answer
➡️ Formula: V₍total₎ = l×b×h
➡️ Substitution: 27 + 8 = l×3×3
➡️ Simplification: 35 = 9l
➡️ Solve: l = 35 ÷ 9 = 3.888… cm
✔️ Final: 3.89 cm (approx.)

🔵 Question 8
Find the total surface area of a cone of radius 6 cm and slant height 10 cm.
🟢 Answer
➡️ Formula: TSA = πrl + πr²
➡️ Substitution: = π(6×10) + π(6²)
➡️ Simplification: = 60π + 36π = 96π cm²
➡️ Numeric: 96×(22/7) = 2112/7 ≈ 301.71 cm²
✔️ Final: ≈ 301.71 cm²

🔵 Question 9
A solid is made by mounting a hemisphere on top of a cylinder of the same radius 5 cm. The cylinder’s height is 12 cm. Find the total surface area of the solid.
🟢 Answer
➡️ Exposed area: TSA = CSA₍cyl₎ + CSA₍hemi₎ + area of circular base
➡️ Formula: = 2πrh + 2πr² + πr²
➡️ Substitution: = 2π×5×12 + 2π×5² + π×5²
➡️ Simplification: = 120π + 50π + 25π = 195π cm²
➡️ Numeric: 195×(22/7) = 4290/7 ≈ 612.86 cm²
✔️ Final: ≈ 612.86 cm²

🔵 Question 10
How many spherical marbles of radius 0.5 cm can be made from a solid cylinder of radius 3 cm and height 4 cm?
🟢 Answer
➡️ Volume of cylinder: V₍cyl₎ = πr²h = (22/7)×3²×4 = 792/7 cm³
➡️ Volume of one sphere: V₍sph₎ = (4/3)πr³ = (4/3)π×0.5³ = π/6 cm³
➡️ Number: N = V₍cyl₎ ÷ V₍sph₎ = (792/7) ÷ (π/6)
➡️ Simplify with π = 22/7: N = (792/7)×(6/π) = (792×6)/(7×22/7) = 2376/11 = 216
✔️ Final: 216 marbles

🔵 Question 11
A metal sheet is rolled into an open cylinder of diameter 14 cm and height 20 cm. Find the area of the sheet used.
🟢 Answer
➡️ Open cylinder ⇒ area = CSA = 2πrh
➡️ Substitution: r = 7 cm, h = 20 cm
➡️ Computation: 2πrh = 2×(22/7)×7×20 = 880 cm²
✔️ Final: 880 cm²

🔵 Question 12
A spherical ball is immersed in water and displaces 3080 cm³ of water. Find the radius of the ball (take π = 22/7).
🟢 Answer
➡️ Formula: V = (4/3)πr³
➡️ Substitution: 3080 = (4/3)×(22/7)×r³
➡️ Simplification: r³ = 3080×3 ÷ (4×22/7) = 9240 ÷ (88/7) = 9240×7 ÷ 88 = 8085 ÷ 11 = 735
➡️ Radius: r = ³√735 ≈ 9.0 cm
✔️ Final: ≈ 9.0 cm

🟡 Section C — Short Answer-II (Q13–Q22, 3 marks each)
(Internal choices are given in Q14, Q16, Q18, Q20.)
🔵 Question 13
A solid metal sphere of radius 3.5 cm is melted and recast into a right circular cylinder of height 4 cm. Find the radius of the cylinder.
🟢 Answer
💡 Volume is conserved: V₍sphere₎ = V₍cylinder₎.
➡️ Formula: (4/3)πr³ = πR²h
➡️ Substitution: (4/3)π×(3.5)³ = π×R²×4
➡️ Simplification: (4/3)×42.875 = 4R²
➡️ Simplification: 57.1667 = 4R²
➡️ R² = 57.1667/4 = 14.2917
➡️ R = √14.2917 ≈ 3.78 cm
✔️ Final: Radius ≈ 3.78 cm

🔵 Question 14
A cylindrical water tank of radius 2 m is filled to a height of 3 m. How many litres of water does it hold? (1 m³ = 1000 L)
🟢 Answer
➡️ Formula: V = πr²h
➡️ Substitution: = (22/7)×2²×3
➡️ Simplification: = (22/7)×4×3 = 264/7 m³
➡️ Value: 264/7 ≈ 37.714 m³
➡️ Convert: 37.714×1000 = 37 714 L
✔️ Final: ≈ 37 714 L
OR
A cylindrical drum of radius 35 cm and height 1 m is completely filled with oil. Find the surface area of the metal sheet in contact with oil (including base, excluding top).
➡️ Formula: Area = CSA + base = 2πrh + πr²
➡️ Substitution: r = 0.35 m, h = 1 m
➡️ Simplification: = 2×π×0.35×1 + π×(0.35)²
➡️ Simplification: = 0.7π + 0.1225π = 0.8225π m²
➡️ Value: 0.8225×3.142 ≈ 2.583 m²
✔️ Final: ≈ 2.583 m²

🔵 Question 15
A cone has slant height 13 cm and radius 5 cm. Find its total surface area.
🟢 Answer
➡️ Formula: TSA = πrl + πr²
➡️ Substitution: = π×5×13 + π×5²
➡️ Simplification: = 65π + 25π = 90π cm²
➡️ Value: 90×(22/7) = 1980/7 ≈ 282.86 cm²
✔️ Final: ≈ 282.86 cm²

🔵 Question 16
A hollow hemispherical bowl has outer radius 10 cm and inner radius 9 cm. Find the outer surface area painted if only the outside is painted (including the circular rim).
🟢 Answer
➡️ Painted area = CSA₍outer hemi₎ + area of annular rim
➡️ Formula: = 2πR² + π(R² − r²)
➡️ Substitution: R = 10, r = 9
➡️ Simplification: = 2π×100 + π(100 − 81)
➡️ Simplification: = 200π + 19π = 219π cm²
➡️ Value: 219×(22/7) = 4818/7 ≈ 688.29 cm²
✔️ Final: ≈ 688.29 cm²
OR
A metal hemisphere of radius 7 cm is kept on a square plate of side 18 cm. Find the total exposed area (hemisphere’s curved surface + plate area not covered by the base circle).
➡️ Exposed area = 2πr² + (18² − πr²)
➡️ Substitution: r = 7
➡️ Simplification: = 2π×49 + (324 − π×49) = (98π) + 324 − 49π = 324 + 49π
➡️ Value: 49×(22/7) = 154 ⇒ 324 + 154 = 478 cm²
✔️ Final: 478 cm²

🔵 Question 17
A frustum of a cone has radii R = 6 cm, r = 4 cm, and height h = 5 cm. Find its volume.
(Use V = (1/3)πh(R² + Rr + r²).)
🟢 Answer
➡️ Formula: V = (1/3)πh(R² + Rr + r²)
➡️ Substitution: = (1/3)π×5×(36 + 24 + 16)
➡️ Simplification: = (5/3)π×76 = 380/3 π cm³
➡️ Value: (380/3)×(22/7) = 8360/21 ≈ 398.10 cm³
✔️ Final: ≈ 398.10 cm³

🔵 Question 18
Rain falls uniformly on a rectangular terrace of size 20 m × 15 m and raises the level of water in a cylindrical tank of radius 3 m by 2 cm. Find the rainfall depth on the terrace.
🟢 Answer
➡️ Volume collected in tank = πr²h
➡️ Substitution: r = 3 m, h = 0.02 m
➡️ Simplification: = π×9×0.02 = 0.18π m³
➡️ Let rainfall depth = d m; terrace area = 20×15 = 300 m²
➡️ Equality: 300×d = 0.18π
➡️ d = (0.18π)/300 = 0.0006π m ≈ 0.001885 m = 1.885 mm
✔️ Final: ≈ 1.89 mm
OR
A road roller is a cylinder of radius 0.7 m and width 1.2 m. How much area will it press in 500 revolutions?
➡️ Area per revolution = CSA strip = circumference×width = 2πr×w
➡️ Substitution: = 2×π×0.7×1.2 = 1.68π m²
➡️ For 500 rev: Area = 500×1.68π = 840π m² ≈ 2639.6 m²
✔️ Final: ≈ 2639.6 m²

🔵 Question 19
A cubical container of side 10 cm is completely filled with water. All the water is poured into a cylindrical beaker of radius 5 cm. Find the rise in water level in the beaker.
🟢 Answer
➡️ Volume transferred = 10³ = 1000 cm³
➡️ Let rise = h cm in cylinder
➡️ Formula: πr²h = 1000
➡️ Substitution: (22/7)×5²×h = 1000
➡️ Simplification: (22/7)×25×h = 1000 ⇒ (550/7)h = 1000
➡️ h = 1000×7/550 = 70/5.5 = 12.727… cm
✔️ Final: ≈ 12.73 cm

🔵 Question 20
A solid wooden toy is made by mounting a cone of height 8 cm and radius 3 cm on a hemisphere of radius 3 cm. Find the total surface area of the toy (base not exposed).
🟢 Answer
➡️ TSA = CSA₍cone₎ + CSA₍hemi₎ = πrl + 2πr²
➡️ Compute l: l = √(r² + h²) = √(3² + 8²) = √73 ≈ 8.544
➡️ Substitution: πrl = π×3×8.544 ≈ 25.632π
➡️ 2πr² = 2π×9 = 18π
➡️ Sum: TSA ≈ (25.632π + 18π) = 43.632π cm² ≈ 137.1 cm²
✔️ Final: ≈ 137.1 cm²
OR
A hemispherical bowl of radius 7 cm is completely filled with soup and poured into cylindrical cups of radius 3.5 cm and height 4 cm. How many cups are needed?
➡️ Volume of bowl = (2/3)πr³ = (2/3)π×7³ = (2/3)π×343 = 686/3 π cm³
➡️ Volume of one cup = πr²h = π×(3.5)²×4 = π×12.25×4 = 49π cm³
➡️ Number = (686/3 π)/(49π) = 686/(147) = 4.666…
➡️ Cups needed = 5 (to hold all soup)
✔️ Final: 5 cups

🔵 Question 21
A right circular cylinder has the same curved surface area as a cone of radius 6 cm and slant height 10 cm. If the cylinder has the same radius, find its height.
🟢 Answer
➡️ CSA₍cyl₎ = 2πrh, CSA₍cone₎ = πrl
➡️ Equality: 2π×6×h = π×6×10
➡️ Simplification: 12h = 60
➡️ h = 5 cm
✔️ Final: 5 cm

🔵 Question 22
A metal pipe is a hollow cylinder with external radius 5 cm, internal radius 4 cm, and length 1 m. Find the volume of metal in the pipe in cm³.
🟢 Answer
➡️ Volume = π(R² − r²)h
➡️ Convert: h = 1 m = 100 cm
➡️ Substitution: = π(5² − 4²)×100 = π(25 − 16)×100
➡️ Simplification: = 9π×100 = 900π cm³
➡️ Value: 900×(22/7) = 19800/7 ≈ 2828.57 cm³
✔️ Final: ≈ 2828.57 cm³

🔴 Section D — Long Answer (Q23–Q30, 4 marks each)
(Internal choices are given in Q24, Q26, Q28.)
🔵 Question 23
A solid comprises a hemisphere of radius 7 cm surmounted by a right circular cone of height 9 cm and the same radius. Find the total surface area of the solid (base not exposed) and its volume.
🟢 Answer
💡 Hemisphere and cone share the base; base circle is internal.
➡️ Formula (TSA): TSA = πrl + 2πr²
➡️ Substitution (l): l = √(r² + h²) = √(7² + 9²) = √(49 + 81) = √130 = √130 cm
➡️ Substitution (TSA): = π×7×√130 + 2π×7²
➡️ Simplification (TSA): = 7π√130 + 98π = (7√130 + 98)π cm²
➡️ Formula (Volume): V = (1/3)πr²h + (2/3)πr³
➡️ Substitution (V): = (1/3)π×7²×9 + (2/3)π×7³
➡️ Simplification (V): = (1/3)π×441 + (2/3)π×343 = (441/3)π + (686/3)π = 1127/3 π cm³
✔️ Final: TSA = (7√130 + 98)π cm²; Volume = (1127/3)π cm³

🔵 Question 24
A frustum of a cone is made by cutting a small cone off the top of a larger cone. The frustum has radii 12 cm and 8 cm, and height 15 cm. Find its curved surface area and volume.
🟢 Answer
➡️ Formula (CSA): CSA = π(R + r)×l
➡️ Substitution (l): l = √(h² + (R − r)²) = √(15² + 4²) = √(225 + 16) = √241 cm
➡️ Substitution (CSA): = π(12 + 8)×√241 = 20π√241 = 20π√241 cm²
➡️ Formula (V): V = (1/3)πh(R² + Rr + r²)
➡️ Substitution (V): = (1/3)π×15×(12² + 12×8 + 8²)
➡️ Simplification (V): = 5π×(144 + 96 + 64) = 5π×304 = 1520π cm³
✔️ Final: CSA = 20π√241 cm²; Volume = 1520π cm³
OR
A metal bucket is a frustum of a cone with top radius 20 cm, bottom radius 12 cm, and depth 24 cm. Find the area of metal sheet used (including the circular base) and the capacity of the bucket.
➡️ CSA: π(R + r)×l, l = √(24² + (20 − 12)²) = √(576 + 64) = √640 = 8√10 cm
➡️ CSA (value): = π(20 + 12)×8√10 = 32π×8√10 = 256π√10 cm²
➡️ Base area: πr² = π×12² = 144π cm²
➡️ Total sheet area: = 256π√10 + 144π = (256√10 + 144)π cm²
➡️ Capacity (volume): (1/3)πh(R² + Rr + r²)
➡️ Substitution: (1/3)π×24×(20² + 20×12 + 12²)
➡️ Simplification: = 8π×(400 + 240 + 144) = 8π×784 = 6272π cm³
✔️ Final: Sheet area = (256√10 + 144)π cm²; Capacity = 6272π cm³

🔵 Question 25
A wooden log is a cylinder of length 3.5 m and diameter 28 cm. It is to be painted on its curved surface only at ₹15 per m². Also find its volume in m³.
🟢 Answer
➡️ Convert: r = 28/2 = 14 cm = 0.14 m, h = 3.5 m
➡️ Formula (CSA): 2πrh
➡️ Substitution (CSA): = 2×π×0.14×3.5
➡️ Simplification (CSA): = 0.98π m²
➡️ Cost: = 0.98π×15 = 14.7π rupees ≈ ₹46.17
➡️ Formula (Volume): πr²h
➡️ Substitution (V): = π×(0.14)²×3.5
➡️ Simplification (V): = π×0.0196×3.5 = 0.0686π m³ ≈ 0.2155 m³
✔️ Final: CSA = 0.98π m²; Cost ≈ ₹46.17; Volume ≈ 0.2155 m³

🔵 Question 26
A solid sphere of radius 6 cm is melted and recast into 8 identical cones each of height 12 cm. Find the radius of each cone.
🟢 Answer
➡️ Volume conservation: (4/3)πR³ = 8×[(1/3)πr²h]
➡️ Substitution: (4/3)π×6³ = 8×(1/3)π×r²×12
➡️ Simplification: (4/3)π×216 = (8/3)π×12×r²
➡️ Simplification: 288π = 32π×r²
➡️ Solve: r² = 288/32 = 9
➡️ Radius: r = 3 cm
✔️ Final: 3 cm
OR
A metallic sphere of radius 9 cm is melted and drawn into a wire of uniform thickness of radius 3 mm. Find the length of the wire.
➡️ Convert: r₍wire₎ = 3 mm = 0.3 cm
➡️ Volume conservation: (4/3)πR³ = πr²L
➡️ Substitution: (4/3)π×9³ = π×(0.3)²×L
➡️ Simplification: (4/3)π×729 = 0.09π×L
➡️ Cancel π: 972 = 0.09×L
➡️ Length: L = 972/0.09 = 10800 cm = 108 m
✔️ Final: 108 m

🔵 Question 27
A conical tent has radius 7 m and slant height 25 m. It is to be made from canvas that is 1.25 m wide. Find the area of canvas required and the number of strips of width 1.25 m needed.
🟢 Answer
➡️ Formula (CSA of cone): πrl
➡️ Substitution (CSA): = π×7×25 = 175π m²
➡️ Area per strip: width × slant height = 1.25×25 = 31.25 m²
➡️ Number of strips: N = (175π)/31.25
➡️ Simplification: N = (175/31.25)×π = 5.6×π ≈ 17.59
➡️ Whole strips needed: 18
✔️ Final: Canvas area = 175π m²; Number of strips = 18

🔵 Question 28
A right circular cylinder just fits inside a right circular cone (their axes coincide). The cone has height 24 cm and base radius 10 cm. The cylinder has height 12 cm. Find the radius of the cylinder and its maximum volume under this fitting condition (similar triangles).
🟢 Answer
➡️ Similarity: r/R = (H − h)/H
➡️ Substitution: r/10 = (24 − 12)/24 = 12/24 = 1/2
➡️ Radius: r = 5 cm
➡️ Volume of cylinder: V = πr²h = π×5²×12 = 300π cm³
✔️ Final: Radius = 5 cm; Volume = 300π cm³
OR
A right triangular prism (base right triangle with legs 6 cm and 8 cm) is melted and recast into a cylinder of height 6 cm. Find the radius of the cylinder.
➡️ Volume conservation: Area₍triangle₎×length = πr²h
➡️ Assume prism length: L = 6 cm (standard unless otherwise stated)
➡️ Triangle area: (1/2)×6×8 = 24 cm²
➡️ Prism volume: 24×6 = 144 cm³
➡️ Cylinder volume: πr²×6 = 144
➡️ Solve: r² = 144/(6π) = 24/π = 24×7/22 = 168/22 = 84/11 ≈ 7.636
➡️ Radius: r = √7.636 ≈ 2.76 cm
✔️ Final: ≈ 2.76 cm

🔵 Question 29
A hollow metal sphere has external radius 9 cm and internal radius 7 cm. It is melted and recast into solid spheres of radius 3 cm. Find the number of solid spheres formed.
🟢 Answer
➡️ Volume (hollow): V = (4/3)π(R³ − r³)
➡️ Substitution: = (4/3)π(9³ − 7³) = (4/3)π(729 − 343)
➡️ Simplification: = (4/3)π×386 = 1544/3 π cm³
➡️ One small sphere: (4/3)π×3³ = (4/3)π×27 = 36π cm³
➡️ Number: N = (1544/3 π)/(36π) = 1544/(108) = 14.296…
➡️ Whole spheres: 14 (with a small leftover)
✔️ Final: 14 spheres

🔵 Question 30
A cistern in the shape of a cylinder of radius 2 m and height 3 m is being filled with water at a rate of 0.1 m³/min while water leaks from the bottom at 0.02 m³/min. How long will it take to fill the cistern from empty?
🟢 Answer
➡️ Net rate: 0.1 − 0.02 = 0.08 m³/min
➡️ Capacity: V = πr²h = π×2²×3 = 12π m³
➡️ Time: t = Volume/Rate = (12π)/0.08 = 150π min
➡️ Value: 150×3.142 ≈ 471.3 min ≈ 7.86 h
✔️ Final: ≈ 7.86 hours

———————————————————————————————————————————————————————————————————————————–

MIND MAP