Class 10 : Maths (In English) – Lesson 11. Areas Related to Circles
EXPLANATION & SUMMARY
🔵 Introduction
⚡ Circles are everywhere—wheels, coins, clocks, tracks.
🌿 This chapter explores areas and perimeters involving full circles and their parts.
🧠 Recall: circumference = 2πr, area = πr².
🟢 1. Perimeter and Area of a Circle – Quick Recall
🔵 Circumference Formula ➡ C = 2πr.
🔴 Area Formula ➡ A = πr².
💡 Concept: π ≈ 3.1416 or 22/7.
✏️ Note: Choose 22/7 when r is a multiple of 7.
✔ Example:
If r = 14 cm:
C = 2 × (22/7) × 14 = 88 cm.
A = (22/7) × 14² = 616 cm².
🟡 2. Areas of Sectors and Segments
🔵 (a) Sector of a Circle
🧭 A sector is enclosed by two radii and the connecting arc.
➤ Central angle = θ (in degrees).
➡ Area of a sector: Aₛₑc = (θ/360) × π r².
➡ Arc length: Lₐᵣc = (θ/360) × 2πr.
🔴 Example:
Find the area of a sector of radius 6 cm, angle 90°.
Aₛₑc = (90/360) × π 6²
= (1/4) × π 36
= 9π cm².
🟢 (b) Segment of a Circle
🌟 A segment is the region between a chord and its arc.
✏️ Note: Segment = Sector − Triangle.
➡ Area of a segment: Aₛₑg = Aₛₑc − ATri
🔵 3. Major and Minor Sectors
🟢 Minor sector: smaller part (< 180°).
🔴 Major sector: larger part (> 180°).
✔ Aₘᵢₙₒᵣ = (θ/360) πr².
✔ Aₘₐⱼₒᵣ = πr² − Aₘᵢₙₒᵣ.
💡 Concept: Major + Minor = πr².
🟡 4. Areas of Composite Figures
⚡ Break complex shapes into simpler ones.
🔵 Compute each area individually.
🟢 Add or subtract as needed.
✔ Keep units consistent.
🟢 5. Perimeter of Composite Figures
🧠 Perimeter = total boundary length.
🌿 Identify arcs and sides forming the boundary.
Example: Rectangle with a semicircle on one side: perimeter = remaining rectangle sides + arc length.
🔴 6. Applications – Track and Path Problems
(a) Circular Track Width
🔵 Outer radius = R, inner radius = r.
🟢 Width = R − r.
🔴 Area_track = π(R² − r²).
(b) Garden Path
➤ Outer radius = r + w.
➡ Area_path = π[(r + w)² − r²] = π(2rw + w²).
🟡 7. Frustum-like or Partial Circular Regions
🟢 Treated as sector differences.
✏️ Note: Distinguish perimeter vs. area.
🔵 8. Derivations Recap
🧠 Arc Length Formula
🟢 Full circle (360°): 2πr.
🔴 For θ°: Lₐᵣc = (θ/360) 2πr.
🧠 Sector Area Formula
🟡 Full circle area: πr².
🔵 For θ°: Aₛₑc = (θ/360) πr².
🟢 9. Worked Examples
Example 1
🔵 Question: Find area of a sector with r = 7 cm, θ = 60°.
🟢 Answer:
➤ Formula: Aₛₑc = (θ/360) πr².
➤ Substitution: (60/360) π 7².
➤ Simplify: (1/6) π 49.
➤ = 49π/6 ≈ 25.67 cm².
✔ Final: 25.67 cm².
Example 2
🔵 Question: Find length of arc for r = 21 cm, θ = 120°.
🟢 Answer:
➤ Formula: Lₐᵣc = (θ/360) 2πr.
➤ Substitution: (120/360) 2π 21.
➤ Simplify: (1/3)(42π).
➤ = 14π ≈ 44 cm.
✔ Final: 44 cm.
Example 3
🔵 Question: Semi-circular window (r = 2 m) on rectangle 4 m × 6 m. Find area.
🟢 Answer:
➤ Rectangle: 4 × 6 = 24 m².
➤ Semi-circle: (1/2) π 2² = 2π m².
➤ Total: 24 + 2π ≈ 30.28 m².
✔ Final: ≈ 30.28 m².
🔴 10. Common Mistakes & Tips
🔵 Sector includes the center; segment does not.
🟢 Always match units.
🟡 Subtract overlapping edges for perimeters.
✏️ Note: Write Formula → Substitution → Simplification → Final answer.
🟢 11. Real-Life Applications
🌿 Wheels, gears, pie-charts, domes, tracks.
🏟️ Athletics track widths (ring areas).
🟡 12. Extra Practice
Example 4
Outer radius = 10 cm, inner = 7 cm.
➤ Area_ring = π(10² − 7²) = π(100 − 49) = π 51.
✔ Final: ≈ 160.22 cm².
Example 5
Garden r = 14 m, path w = 3 m.
➤ Outer radius = 17 m.
➤ Area_path = π(17² − 14²) = π(289 − 196) = π 93.
✔ Final: ≈ 292.19 m².
🔵 13. Segment Example
r = 7 cm, θ = 60°.
➤ Aₛₑc = (60/360) π 7² ≈ 25.67 cm².
➤ Triangle area: (√3/4)(7²) ≈ 21.22 cm².
➤ Segment: 25.67 − 21.22 = 4.45 cm².
✔ Final: 4.45 cm².
🟢 14. Composite Perimeter Example
Semicircle radius = 5 cm plus diameter base.
➤ Arc length = (180/360) 2π5 = π5 = 15.71 cm.
➤ Diameter = 10 cm.
➤ Total = 25.71 cm.
✔ Final: 25.71 cm.
🔴 15. Advanced Fraction of Area
Wheel rotates 50°.
➤ Fraction = 50/360 = 5/36 ≈ 13.9 %.
🟡 16. Playground Example
Rectangle 30 m × 18 m with semicircular ends (r = 9 m).
➤ Rectangle = 540 m².
➤ Two semicircles = π9² = 254.47 m².
➤ Total = 794.47 m².
✔ Final: 794.47 m².
🟢 17. Verification Tip
Estimate rough values to detect mistakes—e.g., r ≈ 10 ⇒ area ≈ 300 cm².
Summary — Areas Related to Circles (≈300 words)
🔵 Core Formulas & Ideas
Circumference: C = 2πr; Area: A = πr².
Sector (central angle θ°):
➤ Area Aₛₑc = (θ/360) × πr²; ➤ Arc length Lₐᵣc = (θ/360) × 2πr.
Segment: Aₛₑg = Aₛₑc − A_△ (subtract area of triangle formed by chord endpoints and center when needed).
Major/Minor sectors: Aₘₐⱼₒᵣ = πr² − Aₘᵢₙₒᵣ; Aₘᵢₙₒᵣ = (θ/360) × πr².
🟢 Composite Figures (Add/Subtract Areas)
Break complex shapes into standard parts (rectangles, triangles, semicircles, quadrants).
Add areas for union; subtract overlaps or holes (e.g., ring/track).
Perimeter of composite shapes: include only boundary parts (arcs + exposed sides), omitting shared edges.
🟡 Special Cases You’ll Meet Often
Ring/Track: A = π(R² − r²) (same center).
Path of width w around a circle: A_path = π[(r + w)² − r²] = π(2rw + w²).
Two semicircles on a rectangle’s shorter side → total semicircle area equals one full circle with that radius.
Semicircle perimeter with diameter base: P = (1/2 of circumference) + diameter = πr + 2r.
🔴 Strategy & Accuracy Tips
Always write: ➤ Formula → ➤ Substitution (with units) → ➤ Simplification → ➤ Final answer (unit).
Choose π = 22/7 or 3.1416 as appropriate; keep unit consistency (cm², m²).
Distinguish sector (includes center) vs segment (bounded by chord and arc).
For segment area, compute the triangle area correctly: use right/isosceles/equilateral formulas or trigonometry as applicable to given θ.
Estimate to sense-check: if r ≈ 10 cm, area ≈ π × 100 ≈ 314 cm².
🌟 Real-Life Connections
Wheels/gears (sector sweep), pie charts (sector fractions), domes/windows (semicircles + rectangles), athletic tracks (ring areas), garden paths (annular regions).
📝 Quick Recap (Exam-Ready)
✔️ C = 2πr, A = πr²; Sector: Aₛₑc = (θ/360)πr²; Arc: Lₐᵣc = (θ/360)2πr.
✔️ Segment = Sector − Triangle (Aₛₑg = Aₛₑc − A△).
✔️ Ring/Track: A = π(R² − r²); Path width w: A = π(2rw + w²).
✔️ Composite figures: split → compute → add/subtract; perimeter = only boundary parts.
✔️ Follow Formula → Substitution → Simplification → Final (with unit), keep units consistent.
✔️ Sense-check magnitudes; distinguish major/minor sectors and sector vs segment clearly.
———————————————————————————————————————————————————————————————————————————–
TEXT BOOK QUESTIONS
🔵 Question
Q1. Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60°.
🟢 Answer
💡 Concept: Aₛₑc = (θ/360) × π r²
🔵 Step 1: Aₛₑc = (60/360) × π × 6²
🔵 Step 2: = (1/6) × π × 36
🔵 Step 3: = 6π
🔵 Step 4: = 6 × (22/7) cm²
✔️ Final: 132/7 cm² ≈ 18.86 cm²
🔵 Question
Q2. Find the area of a quadrant of a circle whose circumference is 22 cm.
🟢 Answer
💡 Concept: C = 2πr, Aquadrant = (1/4) π r²
🔵 Step 1: r = C / (2π) = 22 / (2 × 22/7)
🔵 Step 2: = 22 / (44/7) = (22 × 7) / 44
🔵 Step 3: = 3.5 cm
🔵 Step 4: Acircle = π r² = (22/7) × 3.5²
🔵 Step 5: = (22/7) × 12.25 = 38.5 cm²
🔵 Step 6: Aquadrant = (1/4) × 38.5
✔️ Final: 9.625 cm²
🔵 Question
Q3. The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.
🟢 Answer
💡 Concept: In 60 min → 360°, so in 5 min → 30°. Aₛₑc = (θ/360) π r²
🔵 Step 1: A = (30/360) × π × 14²
🔵 Step 2: = (1/12) × π × 196
🔵 Step 3: = (49/3) π
🔵 Step 4: = (49/3) × (22/7) cm²
✔️ Final: 154/3 cm² ≈ 51.33 cm²
🔵 Question
Q4. A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding: (i) minor segment (ii) major segment. (Use π = 3.14)
🟢 Answer
💡 Concept: Aₛₑg(minor) = Aₛₑc − A△, Amajor = Acircle − Aₛₑg(minor)
🔵 Step 1: Aₛₑc = (90/360) × π × 10² = (1/4) × 3.14 × 100
🔵 Step 2: = 78.5 cm²
🔵 Step 3: A△ = (1/2) × 10² × sin 90° = (1/2) × 100 × 1
🔵 Step 4: = 50 cm²
🔵 Step 5: Aₛₑg(minor) = 78.5 − 50
🔵 Step 6: = 28.5 cm²
🔵 Step 7: Acircle = π r² = 3.14 × 10² = 314 cm²
🔵 Step 8: Amajor = 314 − 28.5
✔️ Final: Minor segment = 28.5 cm²; Major segment = 285.5 cm²
🔵 Question
Q5. In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find: (i) the length of the arc (ii) area of the sector formed by the arc (iii) area of the segment formed by the corresponding chord.
🟢 Answer
💡 Formulas: Lₐᵣc = (θ/360) × 2πr, Aₛₑc = (θ/360) π r², Aₛₑg = Aₛₑc −A△,A△ = (1/2) r² sin θ
🔵 Step 1 (Arc): Lₐᵣc = (60/360) × 2 × (22/7) × 21
🔵 Step 2: = (1/6) × 2 × (22/7) × 21 = (22/7) × 7 = 22 cm
🔵 Step 3 (Sector): Aₛₑc = (60/360) × (22/7) × 21²
🔵 Step 4: = (1/6) × (22/7) × 441 = 231 cm²
🔵 Step 5 (Triangle): A△ = (1/2) × 21² × sin 60°
🔵 Step 6: = (1/2) × 441 × (√3/2) = 441√3 / 4 cm²
🔵 Step 7: Using √3 ≈ 1.732 ⇒A△ ≈ 441 × 1.732 / 4 ≈ 190.99 cm²
🔵 Step 8 (Segment): Aₛₑg = 231 − 190.99
✔️ Final: Lₐᵣc = 22 cm; Aₛₑc = 231 cm²; Aₛₑg ≈ 40.01 cm²
🔵 Question
Q6. A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. (Use π = 3.14 and √3 = 1.73)
🟢 Answer
💡 Concept: Aₛₑg(minor) = Aₛₑc −A△, Amajor = Acircle − Aₛₑg(minor)
🔵 Step 1: Aₛₑc = (60/360) × 3.14 × 15² = (1/6) × 3.14 × 225
🔵 Step 2: = 117.75 cm²
🔵 Step 3: A△= (1/2) × 15² × sin 60° = (1/2) × 225 × (√3/2)
🔵 Step 4: = 225√3 / 4 ≈ 225 × 1.73 / 4 = 97.31 cm²
🔵 Step 5: Aₛₑg(minor) = 117.75 − 97.31 = 20.44 cm²
🔵 Step 6: A_circle = 3.14 × 15² = 706.50 cm²
🔵 Step 7: A_major = 706.50 − 20.44 = 686.06 cm²
✔️ Final: Minor segment ≈ 20.44 cm²; Major segment ≈ 686.06 cm²
🔵 Question
Q7. A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. (Use π = 3.14 and √3 = 1.73)
🟢 Answer
💡 Concept: For 0° < θ ≤ 180°, Aₛₑg = Aₛₑc − A△
🔵 Step 1: Aₛₑc = (120/360) × 3.14 × 12² = (1/3) × 3.14 × 144 = 150.72 cm²
🔵 Step 2: A△= (1/2) × 12² × sin 120° = (1/2) × 144 × (√3/2)
🔵 Step 3: = 72 × (√3/2) = 36√3 cm²
🔵 Step 4: Using √3 = 1.73 ⇒ A_△ ≈ 36 × 1.73 = 62.28 cm²
🔵 Step 5: Aₛₑg = 150.72 − 62.28 = 88.44 cm²
✔️ Final: Aₛₑg ≈ 88.44 cm²
🔵 Question
Q8. A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see Fig. 11.8). Find
(i) the area of that part of the field in which the horse can graze.
(ii) the increase in the grazing area if the rope were 10 m long instead of 5 m. (Use π = 3.14)
🟢 Answer
💡 Concept: From a corner, grazed region is a quarter-circle of radius = rope length.
🔵 Step 1: A₅ = (1/4) × 3.14 × 5² = (1/4) × 3.14 × 25 = 19.625 m²
🔵 Step 2: A₁₀ = (1/4) × 3.14 × 10² = (1/4) × 3.14 × 100 = 78.50 m²
🔵 Step 3: Increase = A₁₀ − A₅ = 78.50 − 19.625 = 58.875 m²
✔️ Final: (i) 19.625 m²; (ii) Increase = 58.875 m²
🔵 Question
Q9. A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in Fig. 11.9. Find :
(i) the total length of the silver wire required.
(ii) the area of each sector of the brooch.
🟢 Answer
💡 Concept: Total wire = circumference + 5 diameters; area/sector = (total area)/10.
🔵 Step 1: Circumference = π d = (22/7) × 35 = 110 mm
🔵 Step 2: Length of 5 diameters = 5 × 35 = 175 mm
🔵 Step 3: Total wire length = 110 + 175 = 285 mm
🔵 Step 4: r = d/2 = 35/2 = 17.5 mm
🔵 Step 5: Acircle = π r² = (22/7) × 17.5² = (22/7) × 306.25
🔵 Step 6: = 962.5 mm²
🔵 Step 7: Area of each sector = 962.5 / 10 = 96.25 mm²
✔️ Final: (i) 285 mm; (ii) 96.25 mm² per sector
🔵 Question
Q10. An umbrella has 8 ribs which are equally spaced (see Fig. 11.10). Assuming umbrella to be a flat circle of radius 45 cm, find the area between two consecutive ribs of the umbrella.
🟢 Answer
💡 Concept: Each pair of ribs subtends θ = 360°/8 = 45°; one sector area = (θ/360) π r².
🔵 Step 1: θ = 45°
🔵 Step 2: Aₛₑc(one) = (45/360) × π × 45²
🔵 Step 3: = (1/8) × π × 2025
🔵 Step 4: = (1/8) × (22/7) × 2025 = (22 × 2025) / 56 cm²
🔵 Step 5: = 44550 / 56 cm² ≈ 795.54 cm²
✔️ Final: ≈ 795.54 cm²
🔵 Question
Q11. A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades.
🟢 Answer
💡 Concept: Each wiper sweeps a sector: Aₛₑc = (θ/360) × π r². Total area = 2 × Aₛₑc.
🔵 Step 1: r = 25 cm, θ = 115°.
🔵 Step 2: Aₛₑc(one) = (115/360) × π × 25².
🔵 Step 3: Aₛₑc(one) = (115/360) × (22/7) × 625 cm².
🔵 Step 4: Atotal = 2 × Aₛₑc(one) = (115/180) × (22/7) × 625 cm².
🔵 Step 5: Simplify fraction (115/180 = 23/36): A_total = (23/36) × (22/7) × 625 cm².
✔️ Final: A_total ≈ 1,254.96 cm² (≈ 1.255 × 10³ cm²).
🔵 Question
Q12. To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships are warned. (Use π = 3.14)
🟢 Answer
💡 Concept: Sector area Aₛₑc = (θ/360) × π r², r in km → area in km².
🔵 Step 1: r = 16.5 km, θ = 80°.
🔵 Step 2: A = (80/360) × 3.14 × 16.5².
🔵 Step 3: 16.5² = 272.25.
🔵 Step 4: A = (80/360) × 3.14 × 272.25.
🔵 Step 5: A = (2/9) × 3.14 × 272.25.
✔️ Final: A ≈ 189.9 km².
🔵 Question
Q13. A round table cover has six equal designs as shown in Fig. 11.11. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of ₹ 0.35 per cm². (Use √3 = 1.7)
🟢 Answer
💡 Concept: The shaded “designs” = area of circle − area of inscribed regular hexagon (side a = radius R).
🔵 Step 1: R = 28 cm ⇒ a = 28 cm.
🔵 Step 2: Area_circle = πR² = (22/7) × 28².
🔵 Step 3: 28² = 784 ⇒ Area_circle = (22/7) × 784 = 22 × 112 = 2464 cm².
🔵 Step 4: Area_hexagon = (3√3/2) a² = (3 × 1.7 / 2) × 28².
🔵 Step 5: (3 × 1.7 / 2) = 2.55; 28² = 784 ⇒ Area_hexagon = 2.55 × 784 = 1999.2 cm².
🔵 Step 6: Area_designs = Area_circle − Area_hexagon = 2464 − 1999.2 = 464.8 cm².
🔵 Step 7: Cost = 0.35 × Area_designs = 0.35 × 464.8.
🔵 Step 8: Cost = ₹162.68.
✔️ Final: Cost ≈ ₹162.68.
🔵 Question
Q14. Tick the correct answer in the following:
Area of a sector of angle p (in degrees) of a circle with radius R is:
🟠 (A) (p/180) × 2πR
🟡 (B) (p/360) × πR²
🟢 (C) (p/360) × 2πR
🔴 (D) (p/720) × 2πR²
🟢 Answer
💡 Concept: Aₛₑc = (θ/360) × πR² with θ = p°.
✔️ Final: Option (B): (p/360) × πR².
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS FOR EXAMS
🔵 Section A – Very Short/Objective (1 mark each)
🔵 Question 1
Find the circumference of a circle of radius 7 cm.
🟢 Options
🔴 A. 14 cm
🟡 B. 21 cm
🟢 C. 44 cm
🔵 D. 22 cm
🧠 Answer
➤ Formula: C = 2πr
➤ Substitution: C = 2 × (22/7) × 7
➤ Simplification: C = 44 cm
✔ Final: C = 44 cm (Option C)
🔵 Question 2
The area of a circle with diameter 14 cm is
🟢 Options
🔴 A. 154 cm²
🟡 B. 308 cm²
🟢 C. 77 cm²
🔵 D. 22 cm²
🧠 Answer
➤ Formula: A = πr², r = d/2 = 7 cm
➤ Substitution: A = (22/7) × 7²
➤ Simplification: A = (22/7) × 49 = 154 cm²
✔ Final: 154 cm² (Option A)
🔵 Question 3
If an arc of a circle subtends a 60° angle at the centre and the radius is 21 cm, its length is
🟢 Options
🔴 A. 11 cm
🟡 B. 22 cm
🟢 C. 21 cm
🔵 D. 44 cm
🧠 Answer
➤ Formula: Lₐᵣc = (θ/360) × 2πr
➤ Substitution: Lₐᵣc = (60/360) × 2 × (22/7) × 21
➤ Simplification: Lₐᵣc = (1/6) × (44/7) × 21 = 22 cm
✔ Final: 22 cm (Option B)
🔵 Question 4
Area of a quadrant of a circle of radius 10 cm is
🟢 Options
🔴 A. 78.5 cm²
🟡 B. 157 cm²
🟢 C. 314 cm²
🔵 D. 25 cm²
🧠 Answer
➤ Formula: A_quadrant = (1/4) πr²
➤ Substitution: A_quadrant = (1/4) × (22/7) × 10²
➤ Simplification: = (1/4) × (22/7) × 100 = 157 cm²
✔ Final: 157 cm² (Option B)
🔵 Question 5
The area of a ring formed by two concentric circles of radii 14 cm and 7 cm is
🟢 Options
🔴 A. 462 cm²
🟡 B. 462 m²
🟢 C. 154 cm²
🔵 D. 308 cm²
🧠 Answer
➤ Formula: A = π(R² − r²)
➤ Substitution: = (22/7)(14² − 7²)
➤ Simplification: = (22/7)(196 − 49) = (22/7)(147) = 462 cm²
✔ Final: 462 cm² (Option A)
🔵 Question 6
A sector of a circle of radius 21 cm has angle 90°. Its area is
🟢 Options
🔴 A. 346.5 cm²
🟡 B. 415.8 cm²
🟢 C. 346.5 m²
🔵 D. 231 cm²
🧠 Answer
➤ Formula: Aₛₑc = (θ/360) πr²
➤ Substitution: = (90/360)(22/7)(21²)
➤ Simplification: = (1/4)(22/7)(441) = (22×63)/4 = 346.5 cm²
✔ Final: 346.5 cm² (Option A)
🟢 Section B – Short Answer I (2 marks each)
🔵 Question 7
Find the perimeter of a semicircular protractor of radius 7 cm (including the diameter).
🧠 Answer
➤ Formula: P = πr + 2r
➤ Substitution: = (22/7) × 7 + 14
➤ Simplification: = 22 + 14 = 36 cm
✔ Final: 36 cm
🔵 Question 8
The minute hand of a clock is 15 cm long. Find the area swept by it in 20 minutes.
🧠 Answer
➤ θ = (20/60) × 360° = 120°
➤ Formula: Aₛₑc = (θ/360) πr²
➤ Substitution: = (120/360)(22/7)(15²)
➤ Simplification: = (1/3)(22/7)(225) = (22×225)/(21) = 4950/21 ≈ 235.7 cm²
✔ Final: ≈ 235.7 cm²
🔵 Question 9
A horse is tied to a peg at one corner of a square field of side 20 m by a rope of length 10 m. Find the grazing area of the horse.
🧠 Answer
➤ Formula: A = (1/4) πr²
➤ Substitution: = (1/4)(3.14)(10²)
➤ Simplification: = 0.25×3.14×100 = 78.5 m²
✔ Final: 78.5 m²
🔵 Question 10
Find the area of a sector of a circle with radius 21 cm if the angle of the sector is 120°.
🧠 Answer
➤ Formula: Aₛₑc = (θ/360) πr²
➤ Substitution: = (120/360)(22/7)(21²)
➤ Simplification: = (1/3)(22/7)(441) = (22×63)/3 = 462 cm²
✔ Final: 462 cm²
🔵 Question 11
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding minor segment. (Use π = 3.14)
🧠 Answer
➤ Formula: Aₛₑg = Aₛₑc − AΔ
➤ Aₛₑc = (90/360)(3.14)(10²) = 78.5 cm²
➤ A△ = (1/2)(10²)(sin 90°) = 50 cm²
➤ Aₛₑg = 78.5 − 50 = 28.5 cm²
✔ Final: 28.5 cm²
🔵 Question 12
Find the length of the arc of a circle with radius 14 cm subtending an angle of 150° at the centre.
🧠 Answer
➤ Formula: Lₐᵣc = (θ/360) × 2πr
➤ Substitution: = (150/360) × 2 × (22/7) × 14
➤ Simplification: = (5/12) × (88) = 36.67 cm
✔ Final: ≈ 36.67 cm
🟡 Section C – Short Answer-II (3 marks each)
🔵 Question 13
Find the area of a sector of a circle with radius 14 cm if the angle of the sector is 150°.
🧠 Answer
➤ Formula: Aₛₑc = (θ/360) π r²
➤ Substitution: = (150/360)(22/7)(14²)
➤ Simplification: = (5/12)(22/7)(196) = (5×22×28)/12 = 3080/12 ≈ 256.67 cm²
✔ Final: ≈ 256.7 cm²
🔵 Question 14
Find the area of a major segment of a circle of radius 10 cm whose minor segment subtends 90° at the centre. (Use π = 3.14)
🧠 Answer
➤ Aₛₑc = (90/360)(3.14)(10²) = 78.5 cm²
➤ A△ = (½)(10²)(sin 90°) = 50 cm²
➤ Minor segment: Aₛₑg = Aₛₑc − A△ = 78.5 − 50 = 28.5 cm²
➤ Circle area: πr² = 3.14×100 = 314 cm²
➤ Major segment: 314 − 28.5 = 285.5 cm²
✔ Final: 285.5 cm²
🔵 Question 15
A circular track has inner radius 33 m and outer radius 35 m. Find the area of the track.
🧠 Answer
➤ Formula: A = π(R² − r²)
➤ Substitution: = (22/7)(35² − 33²)
➤ Simplification: = (22/7)(1225 − 1089) = (22/7)(136) = 2992/7 ≈ 427.43 m²
✔ Final: ≈ 427.4 m²
🔵 Question 16
Find the perimeter of a semicircular window of radius 12 cm (including the diameter).
🧠 Answer
➤ Formula: P = πr + 2r
➤ Substitution: = (22/7)(12) + 24
➤ Simplification: = 264/7 + 24 ≈ 37.71 + 24 = 61.71 cm
✔ Final: ≈ 61.7 cm
🔵 Question 17
A chord of a circle of radius 8 cm subtends an angle of 60° at the centre. Find the area of the minor segment. (Use √3 = 1.73)
🧠 Answer
➤ Aₛₑc = (60/360)πr² = (1/6)(3.14)(64) = 33.49 cm²
➤ A△ = ½ r² sin 60° = ½ (64)(√3/2) = 16√3 = 27.68 cm²
➤ Aₛₑg = 33.49 − 27.68 = 5.81 cm²
✔ Final: ≈ 5.81 cm²
🔵 Question 18
The minute hand of a clock is 12 cm long. Find the area swept by it between 7:05 and 7:20.
🧠 Answer
➤ Time difference = 15 min ⇒ θ = (15/60)×360° = 90°
➤ Aₛₑc = (90/360)πr² = (1/4)(22/7)(12²)
➤ = (1/4)(22/7)(144) = (22×36)/7 = 792/7 ≈ 113.14 cm²
✔ Final: ≈ 113.1 cm²
🔵 Question 19
A brooch is made with silver wire in the form of a circle with diameter 42 mm. The wire is also used in making 6 diameters. Find the total length of the wire.
🧠 Answer
➤ Circumference = πd = (22/7)(42) = 132 mm
➤ Length of 6 diameters = 6×42 = 252 mm
➤ Total wire = 132 + 252 = 384 mm
✔ Final: 384 mm
🔵 Question 20
The radius of a circle is 7 cm. Find the difference between the areas of sectors of angles 60° and 45°.
🧠 Answer
➤ A₆₀ = (60/360)(22/7)(7²) = (1/6)(22/7)(49) = 77/3 ≈ 25.67 cm²
➤ A₄₅ = (45/360)(22/7)(49) = (1/8)(22/7)(49) = 77/4 ≈ 19.25 cm²
➤ Difference = 25.67 − 19.25 = 6.42 cm²
✔ Final: ≈ 6.42 cm²
🔵 Question 21
A horse is tied to a peg at the centre of a circular grass field of radius 21 m. Find the grazing area.
🧠 Answer
➤ Formula: A = πr²
➤ Substitution: = (22/7)(21²) = (22/7)(441)
➤ Simplification: = 1386 m²
✔ Final: 1386 m²
🔵 Question 22 (Internal Choice)
(a) The radius of a wheel is 42 cm. How far will it travel in 100 revolutions?
OR
(b) A circular running track of radius 35 m has width 1.5 m. Find the area of the track.
🧠 Answer (a)
➤ Distance = No. of rev. × Circumference
➤ Circumference = 2πr = 2×(22/7)×42 = 264 cm
➤ Distance = 100 × 264 = 26,400 cm = 264 m
✔ Final: 264 m
🧠 Answer (b)
➤ Outer radius = R = 35 + 1.5 = 36.5 m
➤ Inner radius = r = 35 m
➤ Area = π(R² − r²) = (22/7)(36.5² − 35²)
➤ 36.5² = 1332.25, 35² = 1225
➤ Difference = 107.25
➤ Area = (22/7)(107.25) ≈ 336.9 m²
✔ Final: ≈ 336.9 m²
🔴 Section D — Long Answer (4 × 8 = 32 marks)
🔵 Question 23
A playing field is a rectangle 30 m × 18 m with a semicircle on each of the shorter sides (so radius r = 9 m). Find (i) the perimeter, (ii) the area of the field.
🟢 Answer
➤ Formula (perimeter): P = 2 × (rectangle long side) + (circumference of 1 full circle of radius r)
➤ Substitution: P = 2 × 30 + 2πr = 60 + 2 × (22/7) × 9
➤ Simplification: P = 60 + 396/7 = 60 + 56.57…
✔ Final (i): P ≈ 116.57 m
➤ Formula (area): A = area(rectangle) + area(1 full circle)
➤ Substitution: A = 30 × 18 + π × 9²
➤ Simplification: A = 540 + (22/7) × 81 = 540 + 1782/7 = 540 + 254.57…
✔ Final (ii): A ≈ 794.57 m²
🔵 Question 24 (Internal Choice)
(a) A chord of a circle of radius 10 cm subtends 90° at the centre. Find the area of the minor segment. (Use π = 3.14)
OR
(b) In a circle of radius 14 cm, find the area of the major sector whose central angle is 225°. (Use π = 22/7)
🟢 Answer (a)
➤ Aₛₑc = (90/360) × 3.14 × 10² = 78.5 cm²
➤ A△ = (1/2) × 10² × sin 90° = 50 cm²
➤ Aₛₑg(minor) = Aₛₑc − A△ = 78.5 − 50
✔ Final: 28.5 cm²
🟢 Answer (b)
➤ A_major = (225/360) × (22/7) × 14²
➤ Simplification: = (5/8) × (22/7) × 196 = (5/8) × 616 = 385
✔ Final: 385 cm²
🔵 Question 25
A circular garden of radius 21 m is surrounded by a path of uniform width 3.5 m. Find the area of the path. (Use π = 22/7)
🟢 Answer
➤ Formula: A_path = π[(r + w)² − r²]
➤ Substitution: A_path = (22/7)[(21 + 3.5)² − 21²]
➤ Simplification: (24.5)² − 21² = 600.25 − 441 = 159.25
➤ Apath = (22/7) × 159.25 = 3503.5 / 7 = 500.5
✔ Final: 500.5 m²
🔵 Question 26
A circular track has outer radius 63 m and inner radius 60 m. It is to be tarmacked at ₹ 25 per m². Find the total cost. (Use π = 22/7)
🟢 Answer
➤ Formula: A = π(R² − r²)
➤ Substitution: A = (22/7)(63² − 60²) = (22/7)(3969 − 3600)
➤ Simplification: A = (22/7) × 369 = 8118/7 ≈ 1159.71 m²
➤ Cost = 25 × A = 25 × (8118/7) ≈ 28,992.86
✔ Final: ≈ ₹ 28,992.86
🔵 Question 27 (Internal Choice)
(a) Find the perimeter and area of a semicircular plate of radius 12 cm (include the diameter in perimeter). (Use π = 22/7)
OR
(b) A figure is formed by a rectangle 20 cm × 10 cm surmounted by a semicircle on the 20 cm side. Find the perimeter of the figure. (Use π = 22/7)
🟢 Answer (a)
➤ P = πr + 2r = (22/7) × 12 + 24 = 264/7 + 24 ≈ 61.71 cm
➤ A = (1/2) π r² = (1/2) × (22/7) × 12² = (22 × 72) / 7 = 1584/7 ≈ 226.29 cm²
✔ Final: P ≈ 61.71 cm; A ≈ 226.29 cm²
🟢 Answer (b)
➤ Radius of semicircle r = 20/2 = 10 cm
➤ Boundary parts: two vertical sides + bottom base + top semicircular arc
➤ P = 10 + 10 + 20 + πr = 40 + (22/7) × 10 = 40 + 220/7 ≈ 71.43 cm
✔ Final: ≈ 71.43 cm
🔵 Question 28
In a pie-chart, a sector of angle 72° represents a category. If the radius is 20 cm, find (i) the fraction of the full area, (ii) the length of the arc of the sector. (Use π = 22/7)
🟢 Answer
➤ Fraction f = θ/360 = 72/360 = 1/5
✔ Final (i): 1/5 of total area
➤ Lₐᵣc = (θ/360) × 2πr = (72/360) × 2 × (22/7) × 20
➤ Simplification: Lₐᵣc = (1/5) × (40 × 22/7) = 176/7
✔ Final (ii): Lₐᵣc = 25.14 cm (approx.)
🔵 Question 29 (Internal Choice)
(a) In a circle of radius 15 cm, a chord subtends 120° at the centre. Find the area of the major segment. (Use π = 3.14, √3 = 1.73)
OR
(b) A sector has central angle 135° and radius 10 cm. Find the perimeter of the sector (two radii + arc). (Use π = 22/7)
🟢 Answer (a)
➤ Aₛₑc(minor) = (120/360) × 3.14 × 15² = (1/3) × 3.14 × 225 = 235.50 cm²
➤ A_Δ = (1/2) × 15² × sin 120° = (1/2) × 225 × (√3/2) = 56.25√3 ≈ 97.31 cm²
➤ Aₛₑg(minor) = 235.50 − 97.31 = 138.19 cm²
➤ A_circle = 3.14 × 15² = 706.50 cm²
➤ A_major = 706.50 − 138.19 = 568.31 cm²
✔ Final: A_major ≈ 568.31 cm²
🟢 Answer (b)
➤ Lₐᵣc = (135/360) × 2πr = (3/8) × 2 × (22/7) × 10 = (3/8) × (440/7) = 1320/56 ≈ 23.57 cm
➤ P = 2r + Lₐᵣc = 20 + 23.57 ≈ 43.57 cm
✔ Final: P ≈ 43.57 cm
🔵 Question 30
A round table cloth has radius 1.4 m. A decorative lace is stitched along its boundary at ₹ 45 per metre, and printing is done on the cloth at ₹ 15 per m². Find the total cost. (Use π = 22/7)
🟢 Answer
➤ Circumference: C = 2πr = 2 × (22/7) × 1.4 = 44/5 = 8.8 m
➤ Lace cost = 45 × 8.8 = ₹ 396
➤ Area: A = πr² = (22/7) × (1.4)² = (22/7) × 1.96 = 6.16 m²
➤ Printing cost = 15 × 6.16 = ₹ 92.40
➤ Total cost = 396 + 92.40 = ₹ 488.40
✔ Final: ₹ 488.40
———————————————————————————————————————————————————————————————————————————–
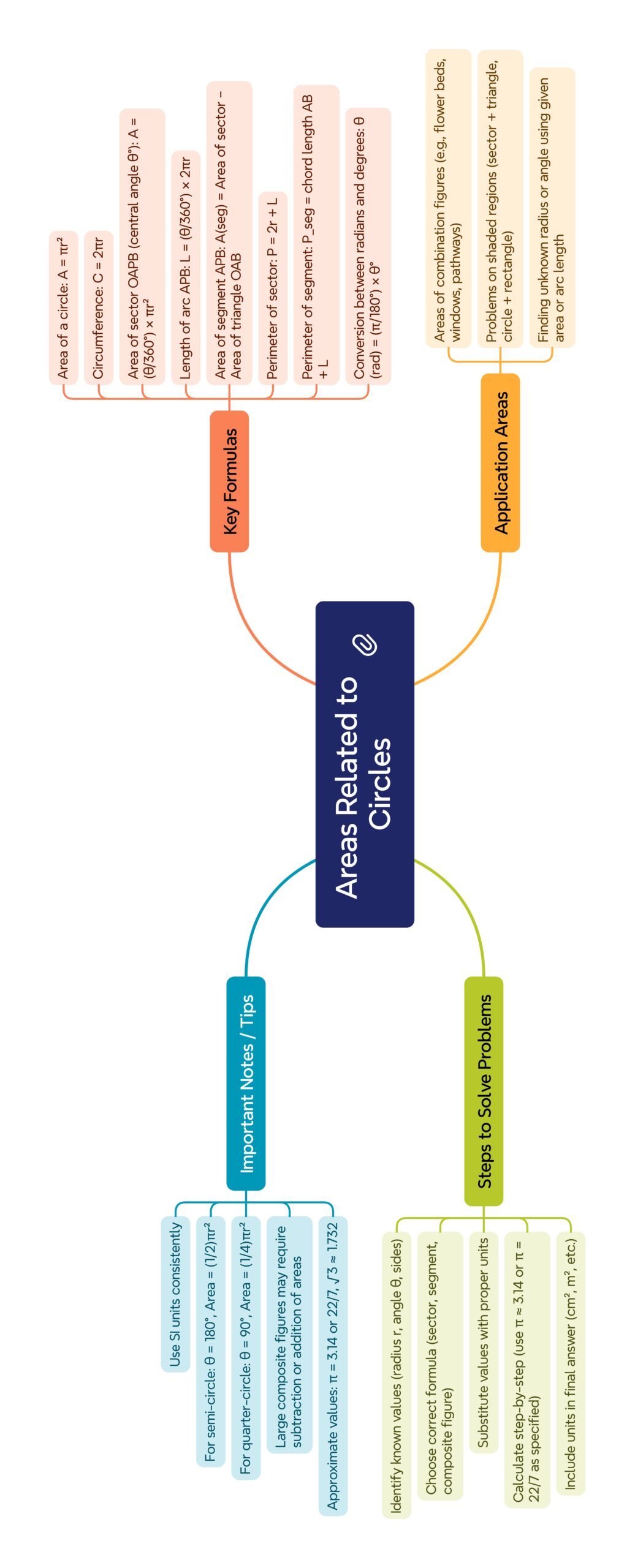
MIND MAP