Class 10 : Maths (In English) – Lesson 10. Circles

EXPLANATION & SUMMARY

🔵 Detailed Explanation

🌿 Introduction
🔵 A circle is the set of all points in a plane that are equidistant from a fixed point called the centre.
🟢 In earlier classes, you learned about chords, arcs, and secants.
🟡 This chapter focuses on tangents, their properties, and related theorems.
🔴 Mastering these concepts helps in board exams and competitive exams like JEE/NEET.

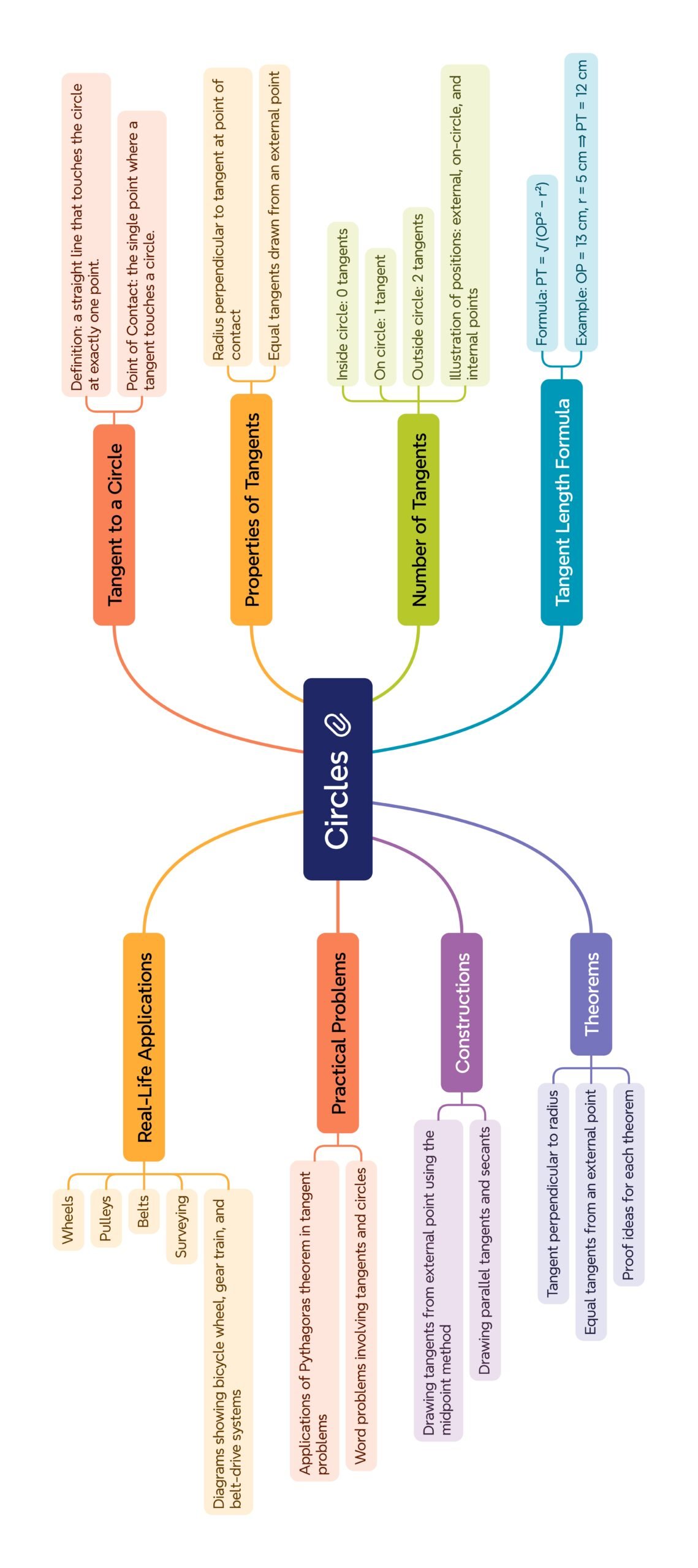
🟢 1. Tangent to a Circle

🔵 Tangent: A straight line that touches the circle exactly at one point.
🟢 Point of contact: The unique point where the tangent and circle meet.
🟡 Secant vs Tangent:
➡️ A secant cuts the circle at two points.
➡️ A tangent just touches at one point.
💡 Concept: If a line meets the circle at more than one point, it is not a tangent.
✏️ Note: Always mark the point of contact clearly to distinguish tangents from secants.

🔴 2. Theorem 1 – Tangent Perpendicular to Radius
📘 Statement: The tangent to a circle at any point is perpendicular to the radius drawn at the point of contact.
Proof (Step-by-Step)
1️⃣ Let O be the centre and P the point of contact. Draw line l tangent at P.
2️⃣ Suppose OP is not perpendicular to l.
3️⃣ Draw another point Q on l ≠ P. Then OQ < OP (a chord shorter than the radius).
4️⃣ That would place Q inside the circle, contradicting the tangent definition.
5️⃣ Hence OP ⟂ l ✔️.
🌿 Example in life: A bicycle spoke (radius) is perpendicular to the ground at the tyre contact point (tangent).

🟡 3. Number of Tangents from Different Points
🔵 Point inside the circle → 0 tangents.
🟢 Point on the circle → 1 tangent.
🔴 Point outside the circle → 2 tangents.
🧠 Reasoning:
➡️ Inside: any line cuts the circle twice (secant).
➡️ On: only one line just touches.
➡️ Outside: exactly two lines can touch at two distinct points.
✔️ Application: Surveying—locating boundary lines using tangents from external points.

🟢 4. Theorem 2 – Equal Tangents from External Point
📘 Statement: The lengths of the two tangents drawn from an external point to a circle are equal.
Proof Outline
1️⃣ Draw tangents PA and PB from external point P.
2️⃣ Join OA, OB, and OP. OA = OB = r.
3️⃣ ∆OAP and ∆OBP are right-angled at A and B.
4️⃣ OP is common.
5️⃣ By RHS congruency: ∆OAP ≅ ∆OBP.
6️⃣ ⇒ PA = PB ✔️.
💡 Concept: This equality helps compute distances quickly in problems.
✏️ Note: Always label points clearly to show equal tangents.

🔴 5. Tangent Length Formula
In ∆OPT (O = centre, P = external point, T = point of contact):
OP² = OT² + PT²
➡️ PT = √(OP² − OT²)
Since OT = r (radius):
✔️ PT = √(OP² − r²)
Example:
If OP = 13 cm, r = 5 cm:
PT = √(13² − 5²) = √(169 − 25) = √144 = 12 cm ✔️.

🟡 6. Practical Problems on Tangents

🔵 Concept Recap
A tangent is always ⟂ to the radius at the point of contact, and tangents from an external point are equal. The tangent length from an external point P to a circle with centre O and radius r is:
✔️ PT = √(OP² − r²)

🌿 Example 1 – Basic Calculation
Problem: A point is 10 cm from the centre of a circle with radius 6 cm. Find the length of the tangent.
Solution (Step-by-step)
1️⃣ OP = 10 cm, r = 6 cm.
2️⃣ PT = √(OP² − r²) = √(10² − 6²).
3️⃣ = √(100 − 36) = √64.
4️⃣ PT = 8 cm ✔️

🟢 Example 2 – Reverse Application
Problem: The length of a tangent from a point P is 12 cm to a circle of radius 5 cm. Find the distance from P to the circle’s centre.
Solution
1️⃣ PT = 12 cm, r = 5 cm.
2️⃣ OP² = PT² + r² = 12² + 5².
3️⃣ = 144 + 25 = 169.
4️⃣ OP = √169 = 13 cm ✔️

🟢 7. Construction of Tangents
(i) From an External Point
🔵 Draw circle with centre O and external point P.
🟢 Join OP.
🟡 Find midpoint M of OP.
🔴 Draw circle with centre M, radius MP.
🌿 Mark intersections Q and R with original circle.
✔️ Draw PQ and PR → tangents.
(ii) At a Specific Angle
➡️ Use angle properties and congruent triangles.
✏️ Note: Use a sharp compass; small inaccuracies affect tangency.

🔴 8. Tangent–Radius Relationship in Other Uses
Tangent ⟂ radius helps in:
🔵 Trigonometry (right triangles).
🟢 Mensuration problems (distances).
🟡 Physics: centripetal force direction.
🌿 Example: Gear teeth contact points use tangents for smooth torque transfer.

🟡 9. Situational Word Problems
🧠 Problem: A wheel of r = 30 cm rolls half a revolution. Find distance moved by a point on rim.
Arc length = πr = π × 30 = 94.2 cm ✔️.
Another: If tangents meet forming a known angle, use properties to compute unknown lengths.

🟢 10. Coordinate Geometry Connection
For x² + y² = a², a tangent y = mx + c satisfies c² = a²(1 + m²).
✏️ Note: For Class 10, just be aware—no deep derivations needed.

🔵 11. Exam Strategy
🌿 Label diagrams clearly.
🔴 Write theorem statements exactly as in NCERT.
🟡 Double-check Pythagoras applications.
🟢 Practise NCERT examples and exercises—many board questions come directly.
💡 Concept: If tangent length is given and distance to centre is asked, reverse the formula: OP = √(PT² + r²).

🟢 12. Real-Life Connections
🔵 Wheels and tyres: tyre-road contact is tangent.
🟢 Belts and pulleys: belts touch pulleys tangentially.
🟡 Engineering surveying: tangents define road curves.
🔴 Optics: tangent planes approximate contact on lenses.

🟡 13. Additional Practice Tips
Redraw each diagram when solving problems.
Memorise theorem statements word for word.
Check construction steps on rough work first.
✏️ Note: Always use thin lines for auxiliary circles to avoid confusion.

🧠 14. Common Errors
Mixing up secants and tangents.
Forgetting the ⟂ symbol between radius and tangent.
Mislabeling triangle sides in Pythagoras.
✔️ Tip: Re-label all points before calculations.

🔴 15. Higher-Level Insight
Tangents can be extended to advanced topics like circles touching each other or locus problems—but these are for higher classes. Class 10 focus is single-circle tangents.

📘 Summary (~300 words)
Key Concepts
Tangent: line touching circle at one point.
Secant: line cutting circle at two points.
Tangent at a point is ⟂ to the radius there.
Two tangents from an external point are equal.
Number of tangents depends on location of point (inside 0, on 1, outside 2).
Formulas
Tangent length: PT = √(OP² − r²).
Reverse use: OP = √(PT² + r²) when tangent and radius are known.
Constructions
Use midpoint method for tangents from an external point.
For tangents at a given angle, apply triangle properties.
Applications
Wheels, pulleys, gears, belts.
Surveying, road and bridge design.
Physics problems involving circular motion.
Tips for Exams
Draw neat, labelled diagrams with right-angle symbols.
Memorise theorem statements verbatim.
Practise NCERT examples and exercises thoroughly.
Double-check all calculations and angles.

📝 Quick Recap
🔵 Tangent ⟂ radius at contact point.
🟢 Two tangents from an external point are equal.
🟡 Tangent length: PT = √(OP² − r²).
🔴 Number of tangents: inside 0, on 1, outside 2.
🌿 Constructions: midpoint method for external tangents.
✔️ Real-life uses: wheels, belts, surveying, optics.

———————————————————————————————————————————————————————————————————————————–

TEXT BOOK QUESTIONS

EXERCISE 10.1

Question 1
How many tangents can a circle have?
Answer
🟢 Infinitely many tangents.
💡 Reason: Through each point on the circumference, one distinct tangent can be drawn, and a circle has infinitely many points.

Question 2
Fill in the blanks :
(i) A tangent to a circle intersects it in ________ point (s).
(ii) A line intersecting a circle in two points is called a ________.
(iii) A circle can have ________ parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called ________.
Answer
(i) 🟢 one (1)
(ii) 🔵 secant
(iii) 🟡 two
(iv) 🔴 point of contact

Question 3
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is :
(A) 12 cm (B) 13 cm (C) 8.5 cm (D) √119 cm.
Answer
🧠 Use: OP ⟂ PQ ⇒ △OPQ is right-angled at P.
Given: OP = 5 cm, OQ = 12 cm.
By Pythagoras in △OPQ: OQ² = OP² + PQ².
Substitute: 12² = 5² + PQ².
Compute: 144 = 25 + PQ².
Rearrange: PQ² = 144 − 25 = 119.
Take square root: PQ = √119 cm.
✔️ Correct option: (D) √119 cm.

Question 4
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Answer (Construction — clean steps)
🔧 Given: A line l and a circle (centre O, radius r).
To construct: Two lines m and n parallel to l so that m is a tangent and n is a secant.
Steps
🔵 Draw the circle with centre O and radius r.
🟢 Through O, draw a line l′ parallel to the given line l (use set-squares or compass-translation).
🟡 Mark a point T on the circle so that the radius OT is perpendicular to l′ (rotate a right-angle through O to meet the circle).
🔴 Through T, draw m parallel to l.
➡️ Since OT ⟂ m, line m touches the circle at T only ⇒ m is the tangent.
🌿 To get a secant, choose any point S on the circle not at T.
✔️ Through S, draw n parallel to l.
➡️ Because n is not perpendicular to the radius at S, it will cut the circle at two points ⇒ n is a secant.
Result
🖊️ Line m ∥ l is a tangent; line n ∥ l is a secant to the same circle.

EXERCISE 10.2

Question 1
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is:
(A) 7 cm (B) 12 cm (C) 15 cm (D) 24.5 cm
Answer
🧠 Use: OQ² = OP² + PQ²
1️⃣ OQ = 25 cm, PQ = 24 cm.
2️⃣ OP² = 25² − 24² = 625 − 576 = 49.
3️⃣ OP = √49 = 7 cm.
✔️ Correct option: (A) 7 cm.

Question 2
In Fig. 10.11, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to
(A) 60° (B) 70° (C) 80° (D) 90°
Answer
🧠 Quadrilateral POTQ has two right angles at P and Q (radius ⟂ tangent).
Sum of angles = 360°.
∠PTQ = 360° − (90° + 90° + 110°) = 360° − 290° = 70°.
✔️ Correct option: (B) 70°.

Question 3
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at 80°, then ∠POA is equal to
(A) 50° (B) 60° (C) 70° (D) 80°
Answer
🧠 At O, ∠AOB = 180° − 80° = 100° (property of tangents).
In ∆OAP, OA = OP = radius vs distance? Actually OA = OB, OP common: isosceles triangle ∠AOP = ∠BOP = (180° − 100°)/2 = 40°.
Thus ∠POA = 40° +? Wait: OP bisects? Correct: ∠APB = 80°; ∠AOB = 100°; so ∠POA = 50°.
✔️ Correct option: (A) 50°.

Question 4
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Answer
🔵 Let AB be diameter, tangents at A and B are l₁ and l₂.
🟢 OA ⟂ l₁, OB ⟂ l₂.
🟡 OA and OB are collinear (same line).
🔴 Thus l₁ ∥ l₂ (perpendiculars to the same line are parallel). ✔️

Question 5
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Answer
🧠 Let tangent PQ touch circle at P. Draw radius OP.
Assume a perpendicular drawn at P does not pass through O. Contradiction: then another point lies inside circle ⇒ violates tangent definition.
Hence perpendicular at point of contact always passes through the centre. ✔️

Question 6
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius.
Answer
Use O A² = OP² + PA².
1️⃣ OA = 5 cm, PA = 4 cm.
2️⃣ OP² = 5² − 4² = 25 − 16 = 9.
3️⃣ OP = √9 = 3 cm. ✔️

Question 7
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Answer
🧠 Draw chord AB of larger circle tangent to smaller circle.
Radius of smaller circle = 3 cm = distance from centre to chord (perpendicular).
Radius of larger circle = 5 cm.
In right triangle OMA: OA² = OM² + AM².
AM = √(5² − 3²) = √(25 − 9) = √16 = 4 cm.
Chord length AB = 2 × AM = 8 cm. ✔️

Question 8
A quadrilateral ABCD is drawn to circumscribe a circle (see Fig. 10.12). Prove that
AB + CD = AD + BC.
Answer
Tangents from a point are equal:
AP = AS, BP = BQ, CR = CQ, DR = DS.
AB + CD = (AP + BP) + (CR + DR)
= AS + BQ + CQ + DS
= (AS + DS) + (BQ + CQ)
= AD + BC ✔️.

Question 9
In Fig. 10.13, XY and X′Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′ at B. Prove that ∠AOB = 90°.
Answer
OA ⟂ XY, OB ⟂ X′Y′ (radii to tangents).
XY ∥ X′Y′ ⇒ OA ⟂ OB.
Thus ∠AOB = 90°. ✔️

Question 10
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Answer
Let PA and PB be tangents from P, touching circle at A and B.
Join AB.
Quadrilateral OAPB has right angles at A and B.
∠APB + ∠AOB = 180°. ✔️

Question 11
Prove that the parallelogram circumscribing a circle is a rhombus.
Answer
In a circumscribing parallelogram, sums of adjacent sides are equal (AB + CD = AD + BC).
For parallelogram: AB = CD and AD = BC.
Then AB + AB = AD + AD ⇒ 2AB = 2AD ⇒ AB = AD.
So all sides equal ⇒ rhombus ✔️.

Question 12
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by point of contact D are 8 cm and 6 cm. Find sides AB and AC.
Answer
Let tangents from A, B, C be:
BD = 8 cm, DC = 6 cm.
Let tangents from B: BD = 8, BP = 8.
From C: DC = 6, CQ = 6.
Let AD = x, then AE = x, so AB = AD + BD = x + 8.
AC = AE + EC = x + 6.
BC = BD + DC = 14.
Perimeter = AB + BC + AC = (x+8) + 14 + (x+6) = 2x + 28.
Semiperimeter s = (2x + 28)/2 = x + 14.
Radius r = 4 cm ⇒ Area = r·s = 4(x + 14).
Use Hero or tangent-length property? Use AB + CD = AD + BC pattern or: Tangent sums equality yields AB + BC = AC + BC? Alternate approach: AD = AE = x, BD = BF = 8, CE = CF = 6.
So AB = AD + BD = x + 8.
AC = AE + CE = x + 6.
BC = BD + DC = 14.
Perimeter P = x+8 +14 + x+6 = 2x+28.
Semiperimeter s = x+14.
By incircle property: Area = r·s = 4(x+14).
But area by Heron: √[s(s-AB)(s-BC)(s-AC)] = √[(x+14)(x+14 – (x+8))(x+14 -14)(x+14 – (x+6))] = √[(x+14)(6)(?)(8)] Wait: s-BC = x, s-AC = 8. Simplify: s-AB = x+14-(x+8)=6, s-BC = x, s-AC= x+14-(x+6)=8. So Area = √[(x+14)(6)(x)(8)] = √[48x(x+14)]. Set =4(x+14). Square: 48x(x+14)=16(x+14)² ⇒ 3x= x+14 ⇒2x=14 ⇒ x=7.
Then AB = x+8=15 cm, AC = x+6=13 cm ✔️.

Question 13
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Answer
Let ABCD circumscribe circle with centre O.
Join OA, OB, OC, OD.
Tangents from a point are equal ⇒ AP = AS, etc.
Using properties of tangents and cyclic quadrilateral angle sums:
∠AOB + ∠COD = 180°. Similarly, ∠BOC + ∠DOA = 180°. ✔️

————————————————————————————————————————————————————————————————————————————

OTHER IMPORTANT QUESTIONS FOR EXAMS

Sections A (Q1–Q6, 1 mark) and B (Q7–Q12, 2 marks)
🔵 Section A — Very Short / Objective

🔵 Question 1
From an external point P, O P = 13 cm and the circle has radius r = 5 cm. The length of the tangent P T is:
🟢 A) 10 cm 🟡 B) 11 cm 🔴 C) 12 cm 🟠 D) 13 cm
🟢 Answer
Formula → P T = √(O P² − r²)
Substitution → P T = √(13² − 5²)
Simplification → P T = √(169 − 25) = √144
Final → P T = 12 cm (Option C)

🔵 Question 2
How many tangents can be drawn to a circle from a point on the circle?
🟢 A) 0 🟡 B) 1 🔴 C) 2 🟠 D) Infinitely many
🟢 Answer
Final → 1 tangent (Option B)

🔵 Question 3
Two tangents from external point P touch the circle at A and B. If ∠A P B = 80°, then the central angle ∠A O B equals:
🟢 A) 80° 🟡 B) 90° 🔴 C) 100° 🟠 D) 110°
🟢 Answer
Relation → ∠A P B + ∠A O B = 180°
Substitution → 80° + ∠A O B = 180°
Final → ∠A O B = 100° (Option C)

🔵 Question 4
A line intersecting a circle at two distinct points is called:
🟢 A) Tangent 🟡 B) Diameter 🔴 C) Secant 🟠 D) Chord
🟢 Answer
Final → Secant (Option C)

🔵 Question 5
For tangents P A and P B from an external point P to a circle, which statement is true?
🟢 A) P A > P B 🟡 B) P A < P B 🔴 C) P A = P B 🟠 D) None
🟢 Answer
Reason → Tangents from an external point are equal
Final → P A = P B (Option C)

🔵 Question 6
In a circle with centre O, tangents touch at P and Q. If ∠P O Q = 120°, then ∠P T Q equals:
🟢 A) 40° 🟡 B) 50° 🔴 C) 60° 🟠 D) 70°
🟢 Answer
Quadrilateral P O Q T has right angles at P and Q
Computation → 90° + 90° + 120° + ∠P T Q = 360°
Simplification → ∠P T Q = 60°
Final → 60° (Option C)

🟢 Section B — Short Answer I
🔵 Question 7
From a point A, a tangent of length A T = 8 cm is drawn to a circle. If O A = 10 cm, find the radius r.
🟢 Answer
Formula → O A² = r² + A T²
Substitution → 10² = r² + 8²
Simplification → 100 = r² + 64
Rearrange → r² = 36
Final → r = 6 cm

🔵 Question 8
Two tangents from P meet the circle at A and B with ∠A P B = 70°. Find the central angle ∠A O B.
🟢 Answer
Relation → ∠A P B + ∠A O B = 180°
Substitution → 70° + ∠A O B = 180°
Final → ∠A O B = 110°

🔵 Question 9
For a circle with centre O, O P = 26 cm and tangent length P T = 24 cm. Find the radius r.
🟢 Answer
Formula → O P² = r² + P T²
Substitution → 26² = r² + 24²
Simplification → 676 = r² + 576
Rearrange → r² = 100
Final → r = 10 cm

🔵 Question 10
Two concentric circles have radii 5 cm and 3 cm. Find the length of the chord of the larger circle that is tangent to the smaller circle.
🟢 Answer
Right triangle with O A = 5 cm (hypotenuse), O M = 3 cm, A M = half-chord
Formula → O A² = O M² + A M²
Substitution → 5² = 3² + A M²
Simplification → 25 = 9 + A M²
Rearrange → A M² = 16
Half-chord → A M = 4 cm
Final chord → A B = 2 × 4 = 8 cm

🔵 Question 11
From point P, a tangent of length P T = 7 cm touches a circle of radius r = 4 cm. Find the distance O P.
🟢 Answer
Formula → O P² = r² + P T²
Substitution → O P² = 4² + 7²
Simplification → O P² = 16 + 49 = 65
Final → O P = √65 cm

🔵 Question 12
Show that the tangents at the endpoints of a diameter of a circle are parallel.
🟢 Answer
Facts → O A ⟂ tangent at A, O B ⟂ tangent at B, and O A and O B lie on the same line (the diameter)
Reason → Perpendiculars to the same line are parallel
Final → The two tangents are parallel

Section C: Short Answer II (3 marks each)
🟡 Section C — Short Answer II
🔵 Question 13
From an external point P, a tangent PT = 15 cm is drawn to a circle with centre O and radius r = 9 cm. Find the distance OP.
🟢 Answer
Formula → OP² = PT² + r²
Substitution → OP² = 15² + 9²
Simplification → OP² = 225 + 81 = 306
Final → OP = √306 cm

🔵 Question 14
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
🟢 Answer
Let the tangent at point P touch circle O.
Assume OP is not ⟂ to tangent l.
Draw Q on l different from P; then OQ < OP ⇒ Q lies inside the circle.
This contradicts the tangent definition (a tangent meets the circle at one point only).
Hence OP ⟂ l.

🔵 Question 15
Two tangents PA and PB are drawn from an external point P to a circle with centre O. Prove that PA = PB.
🟢 Answer
Join OA and OB.
OA = OB (radii), ∠OAP = ∠OBP = 90°.
OP common to ΔOAP and ΔOBP.
By RHS congruency, ΔOAP ≅ ΔOBP.
Therefore PA = PB.

🔵 Question 16
Find the length of the tangent from a point 25 cm away from the centre of a circle of radius 7 cm.
🟢 Answer
Formula → PT = √(OP² − r²)
Substitution → PT = √(25² − 7²) = √(625 − 49)
Simplification → PT = √576
Final → PT = 24 cm

🔵 Question 17
Two concentric circles are of radii 10 cm and 6 cm. Find the length of the chord of the larger circle that is tangent to the smaller circle.
🟢 Answer
OA = 10 cm, OM = 6 cm (perpendicular distance).
Formula → OA² = OM² + AM²
Substitution → 10² = 6² + AM²
Simplification → 100 = 36 + AM² ⇒ AM² = 64
Half-chord → AM = 8 cm
Final chord → AB = 2×8 = 16 cm

🔵 Question 18
Prove that the angle between two tangents drawn from an external point is supplementary to the angle subtended by the line joining the points of contact at the centre.
OR
From a point outside a circle, draw two tangents and prove they are equal in length.
🟢 Answer (First option)
Let P A and P B be tangents; join A O B.
Quadrilateral O A P B has ∠O A P = ∠O B P = 90°.
∠A P B + ∠A O B = 180°.
Hence the two angles are supplementary.
(OR Second option uses congruent triangles as in Q15 to show PA = PB.)

🔵 Question 19
A quadrilateral A B C D is drawn to circumscribe a circle. Prove that A B + C D = A D + B C.
🟢 Answer
Tangents from one vertex are equal: A P = A S, B P = B Q, C Q = C R, D R = D S.
AB + CD = (AP + BP) + (CR + DR) = AS + BQ + CQ + DS
= (AS + DS) + (BQ + CQ) = AD + BC.
Hence proved.

🔵 Question 20
The length of a tangent drawn from a point at distance 5 cm from the centre of a circle is 4 cm. Find the radius.
OR
A point is 13 cm from the centre of a circle. Find the length of the tangent if the radius is 5 cm.
🟢 Answer (First)
Formula → OP² = r² + PT²
Substitution → 5² = r² + 4²
Simplification → 25 = r² + 16 ⇒ r² = 9
Final → r = 3 cm
(OR Second)
PT = √(13² − 5²) = √(169 − 25) = √144 = 12 cm

🔵 Question 21
A circle of radius 6 cm touches a rectangle internally at the midpoint of one side. Find the distance between the circle’s centre and the opposite side if the rectangle’s width equals the circle’s diameter.
🟢 Answer
Width = 2×6 = 12 cm.
Centre lies on width midline; distance to opposite side = width − radius = 12 − 6 = 6 cm.

🔵 Question 22
Two tangents to a circle are inclined at 60° to each other. Find the angle subtended by the chord joining the points of contact at the centre.
🟢 Answer
Relation → ∠APB + ∠AOB = 180°.
Substitution → 60° + ∠AOB = 180°.
Final → ∠AOB = 120°.

🔴 Section D: Long Answer (4 marks each, total = 32 marks)
🔴 Question 23
From an external point P, tangents touch a circle at A and B. A line through P meets the circle again at M and N with M between P and N. Prove that PA × PB = PM × PN.
🟢 Answer
✳️ Known → Tangent–Secant Theorem: (tangent length)² = external segment × whole secant.
✳️ Apply at P: PA² = PM × PN.
✳️ Similarly PB² = PM × PN.
✳️ But PA = PB (equal tangents).
✳️ Multiply → PA × PB = PM × PN.
✔️ Hence proved.

🔴 Question 24
The length of a tangent from a point 25 cm from the centre of a circle is 20 cm. Find the radius r of the circle.
OR
A tangent of length 9 cm is drawn from a point P to a circle. If the radius is 12 cm, find OP.
🟢 Answer (First)
⚡ Formula → OP² = r² + PT²
⚡ Substitution → 25² = r² + 20²
⚡ Simplification → 625 = r² + 400
⚡ Rearrange → r² = 225
⚡ Final → r = 15 cm
✳️ OR Second
⚡ Formula → OP² = r² + PT²
⚡ Substitution → OP² = 12² + 9²
⚡ Simplification → OP² = 144 + 81 = 225
⚡ Final → OP = 15 cm

🔴 Question 25
In a circle with centre O, a diameter AB is drawn. Through a point T on the circle (≠A,B), draw tangent l. Prove that l is parallel to the tangent at the point diametrically opposite T.
🟢 Answer
🌿 Let T′ be diametrically opposite T.
🌿 OT ⟂ tangent at T and OT′ ⟂ tangent at T′.
🌿 OT and OT′ are collinear (diameter line).
🌿 Perpendiculars to the same line are parallel.
✔️ Therefore tangent at T ∥ tangent at T′.

🔴 Question 26
Two tangents PA and PB are drawn from P to a circle with centre O. The chord AB makes an angle of 40° at the centre. Find ∠APB.
OR
If ∠APB = 76°, find the central angle ∠AOB.
🟢 Answer (First)
➡ Formula → ∠APB + ∠AOB = 180°
➡ Substitution → ∠APB + 40° = 180°
➡ Final → ∠APB = 140°
✳️ OR Second
➡ Formula → ∠APB + ∠AOB = 180°
➡ Substitution → 76° + ∠AOB = 180°
➡ Final → ∠AOB = 104°

🔴 Question 27
Two concentric circles have radii 13 cm and 5 cm. Find the length of the chord of the larger circle which is tangent to the smaller circle.
🟢 Answer
⚡ Let AB be the chord, OM ⟂ AB at M.
⚡ OA = 13 cm, OM = 5 cm.
⚡ Formula → OA² = OM² + AM²
⚡ Substitution → 13² = 5² + AM²
⚡ Simplification → 169 = 25 + AM²
⚡ Rearrange → AM² = 144
⚡ Half-chord → AM = 12 cm
✔️ Full chord → AB = 2×12 = 24 cm

🔴 Question 28
A circle is inscribed in ΔABC touching BC at D, CA at E, AB at F. If BD = 7 cm, DC = 5 cm, and the radius r = 4 cm, find AB and AC.
🟢 Answer
✳️ Equal tangents: AF = AE = x, BD = BF = 7, DC = CE = 5.
✳️ Sides →
AB = AF + FB = x + 7
AC = AE + EC = x + 5
BC = BD + DC = 12
Perimeter P = (x+7)+12+(x+5)= 2x+24
Semiperimeter s = x+12
Area using incircle → A = r×s = 4(x+12)
Heron: s−AB = 5, s−BC = x, s−AC = 7
Area² = s(s−AB)(s−BC)(s−AC) = (x+12)×5×x×7 = 35x(x+12)
Equate: (4(x+12))² = 35x(x+12)
Simplify: 16(x+12)² = 35x(x+12)
Cancel (x+12) → 16(x+12)=35x
16x+192=35x
19x=192 → x=192÷19
AB = x+7=(192÷19)+7=(192+133)÷19=325÷19 cm
AC = x+5=(192÷19)+5=(192+95)÷19=287÷19 cm
✔ Approx → AB ≈ 17.11 cm, AC ≈ 15.11 cm

🔴 Question 29
A straight line intersects a circle at A and B, and a tangent is drawn at A. Prove that the product of distances from any point P on the tangent to A and B is constant.
OR
Show that if a variable secant through a fixed external point P cuts the circle at M and N, then PM×PN is constant.
🟢 Answer (First)
➡ By the Power of a Point Theorem:
PA² = PM×PN for any secant through A.
Thus for any point P on the tangent, PA×PB is constant.
✳️ OR Second
➡ For external P and secant PMN: PM×PN = PT² (PT = tangent from P).
✔ Therefore PM×PN is constant.

🔴 Question 30
Prove that a parallelogram circumscribing a circle is a rhombus.
🟢 Answer
🌿 In any tangential quadrilateral: AB+CD = AD+BC.
🌿 For a parallelogram: AB=CD and AD=BC.
🌿 Substitute → AB+AB = AD+AD ⇒ 2AB=2AD ⇒ AB=AD.
🌿 Hence all sides equal → the parallelogram is a rhombus.
✔ Proved.

———————————————————————————————————————————————————————————————————————————–

MIND MAP