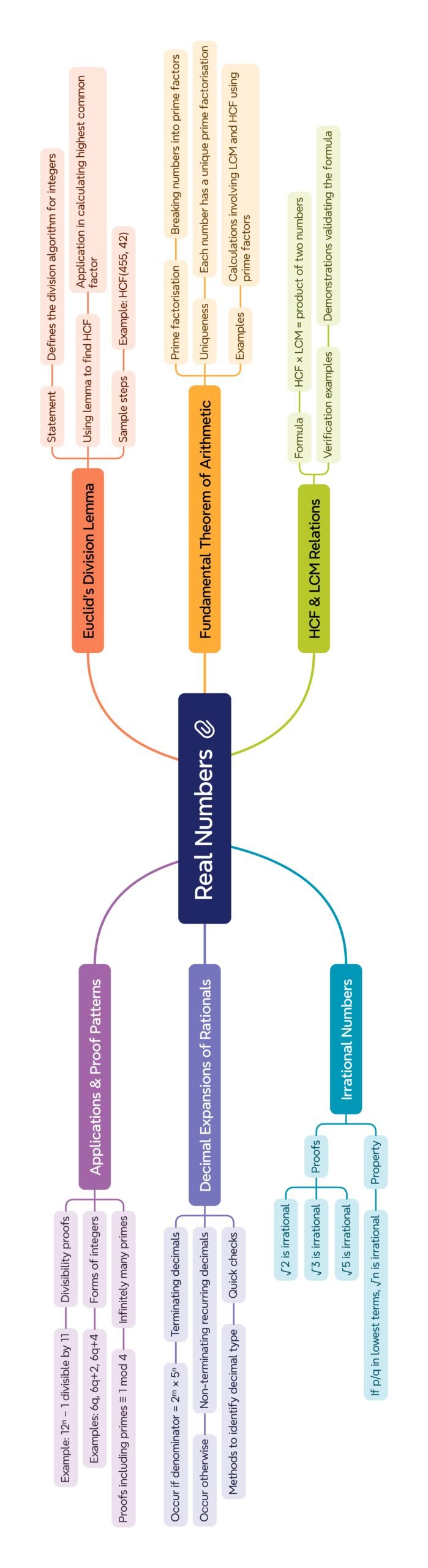
Class 10 : Maths (In English) – Lesson 1. Real Numbers
EXPLANATION & SUMMARY
🔵 Detailed Explanation
🔵 1) Introduction 🌿
• The set of real numbers ℝ consists of rational numbers (ℚ) and irrational numbers (ℝ \ ℚ).
• Rational numbers include integers, fractions, terminating, and recurring decimals.
• Irrational numbers include √2, π, non-repeating non-terminating decimals.
• Real numbers are closed under addition, subtraction, multiplication, and division (except ÷ 0).
💡 Concept: Real numbers can be represented as unique points on the number line — no gaps exist.
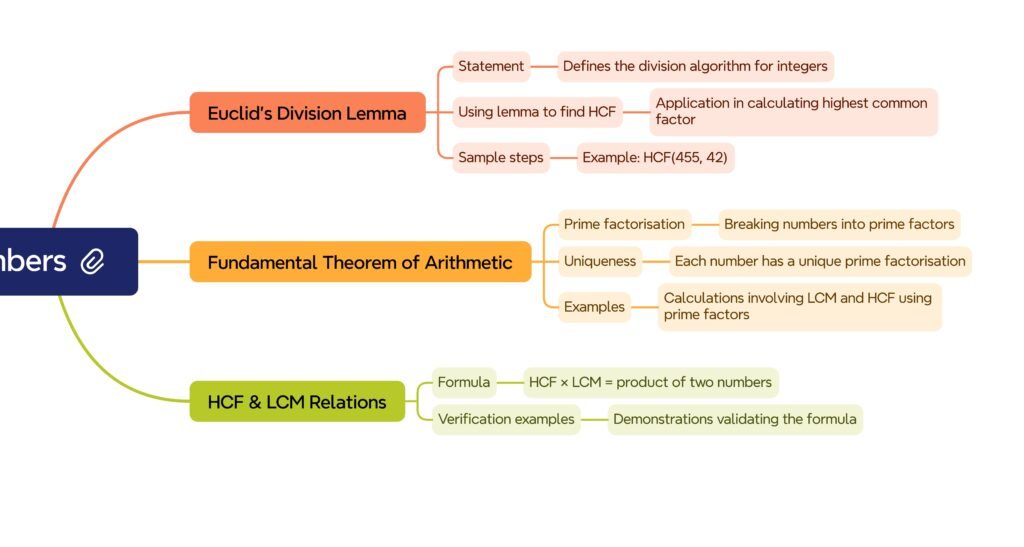
🟢 2) Euclid’s Division Lemma ⚡
• For any two positive integers a and b, ∃ unique integers q and r such that
a = bq + r, where 0 ≤ r < b.
• Example: Divide 225 by 7: 225 = 7×32 + 1 (q=32, r=1).
✏️ Note: This lemma forms the basis for the Euclidean algorithm to compute HCF.
🟡 3) Euclidean Algorithm for HCF ➡️
Steps:
1️⃣ Apply division lemma repeatedly until remainder r=0.
2️⃣ The divisor at this step is HCF(a,b).
Example: Find HCF(455, 42):
455 = 42×10 + 35.
42 = 35×1 + 7.
35 = 7×5 + 0 ⇒ HCF=7.
🔴 4) Fundamental Theorem of Arithmetic 🌿
• Every composite number >1 can be expressed uniquely (apart from order) as a product of primes.
Example: 84=2²×3×7.
💡 Concept: This theorem ensures factorisation consistency.
🔵 5) Applications of FTA ✔️
• HCF & LCM: Use prime factorisation.
Example: HCF(6,20)=2; LCM(6,20)=60.
• Proving irrationality:
– √2 is irrational: If √2=p/q ⇒2=p²/q² ⇒p² even ⇒p even ⇒q even ⇒contradiction.
– Similarly √3, √5 are irrational.
🟢 6) Terminating & Non-Terminating Decimals 🧠
• Let x=p/q in lowest terms.
• x has terminating decimal ⇔ denominator q=2ⁿ5ᵐ.
• If q has prime factors other than 2 or 5 ⇒ decimal is non-terminating repeating.
Example: 13/40 terminates (40=2³×5).
Example: 7/12 repeats (12=2²×3).
🟡 7) Decimal Examples ➡️
• Convert recurring decimals to fractions:
x=0.35̅ ⇒100x=35.35̅ ⇒100x−x=35⇒99x=35⇒x=35/99.
🔴 8) Revisiting Irrationals 🌿
• Proof by contradiction is standard.
• Sum/Difference Rules:
– If r rational ≠0, and x irrational, then r+x and r×x are irrational.
✏️ Note: The product of two irrationals can be rational (e.g., √2×√2=2).
🔵 9) HCF×LCM Property ✔️
For positive integers a,b: HCF(a,b) × LCM(a,b) = a × b.
🟢 10) Real-Life Examples 🧠
• Gear cycles: teeth counts’ HCF for smooth rotation.
• Traffic light timers: LCM ensures simultaneous green intervals.
• Decimal classification for financial calculations (currency, interest rates).
🟡 11) Practice Problem 🌿
Find if 21/150 has terminating decimal:
Simplify 21/150=7/50=7/(2×5²) → only 2 and 5 → terminating.
🔴 12) More on Euclid’s Lemma ✔️
• To prove infinitude of primes: Assume finitely many p₁,…,pₙ. Consider N=p₁×…×pₙ+1. N divisible by none ⇒ contradiction ⇒ infinite primes.
🔵 13) Important Proof Sketch ✏️
• To prove 3.1022… repeating is rational: represent as p/q using subtraction trick.
🟢 14) Misconceptions 🌿
• Believing all roots are irrational (√4=2 is rational).
• Assuming two irrationals always give irrational product.
🟡 15) Applications Beyond School ⚡
• Cryptography uses prime factorisation.
• Computer algorithms use Euclid’s algorithm for efficiency.
• Engineering: Gear ratios & wave harmonics depend on LCM/HCF.
🔴 16) Summary Table of Quadrant (Not needed here)
Skipped, as unrelated.
🔵 17) Practice & Self-Check ✔️
1️⃣ Prove √5 is irrational.
2️⃣ Find HCF & LCM of 306 and 657 using prime factorisation.
3️⃣ Check if 77/160 is terminating.
4️⃣ Find HCF(96,128) using Euclid’s algorithm.
5️⃣ Show HCF×LCM=a×b for 12 and 18.
🟣 Summary (~300 words)
Real Numbers Overview
• Real numbers = rationals ℚ + irrationals ℝ\ℚ.
• Closed under basic operations.
Euclid’s Division Lemma & Algorithm
• a=bq+r, 0≤r<b.
• Repeated division finds HCF.
Fundamental Theorem of Arithmetic
• Every composite number factors uniquely into primes.
• Used to find HCF, LCM, and prove irrationality.
Decimal Expansions
• Terminating ⇔ denominator=2ⁿ5ᵐ.
• Otherwise repeating.
• Recurring decimals convertible to fractions.
Irrational Proofs
• √2, √3, √5 irrational (contradiction method).
• Infinite primes via Euclid’s lemma.
Applications
• LCM in traffic signals, gear synchronization.
• HCF in reducing fractions, packaging.
• Cryptography & computing efficiency.
Key Property
• HCF×LCM=a×b.
Mastering these ideas bridges arithmetic and algebra, preparing for advanced number theory and practical problem-solving.
📝 Quick Recap
🔵 Real numbers=ℚ∪(ℝ\ℚ).
🟢 Euclid’s division lemma: a=bq+r.
🟡 Fundamental theorem: unique prime factorisation.
🔴 Terminating decimals: denominator=2ⁿ5ᵐ.
🔵 HCF×LCM=a×b.
✨ Applications: cryptography, gears, timers.
————————————————————————————————————————————————————————————————————————-
TEXT BOOK QUESTIONS
Exercise 1.1
🔵 Question
Express each number as a product of its prime factors:
(i) 140 (ii) 156 (iii) 3825 (iv) 5005 (v) 7429
🟢 Answer
💡 Concept: Prime factorisation via division or splitting into known factors.
🔵 Step (i): 140 = 2 × 70 = 2 × 2 × 35 = 2² × 5 × 7
✔️ Final (i): 2² × 5 × 7
🔵 Step (ii): 156 = 2 × 78 = 2 × 2 × 39 = 2² × 3 × 13
✔️ Final (ii): 2² × 3 × 13
🔵 Step (iii): 3825 = 5 × 765 = 5 × 5 × 153 = 5² × 153 = 5² × 3 × 51 = 5² × 3 × 3 × 17
✔️ Final (iii): 3² × 5² × 17
🔵 Step (iv): 5005 = 5 × 1001 = 5 × (7 × 11 × 13)
✔️ Final (iv): 5 × 7 × 11 × 13
🔵 Step (v): 7429 = 17 × 437 = 17 × (19 × 23)
✔️ Final (v): 17 × 19 × 23
🔵 Question
2. Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers.
(i) 26 and 91 (ii) 510 and 92 (iii) 336 and 54
🟢 Answer
✳️ (i) 26 and 91
🔵 Step 1: 26 = 2 × 13; 91 = 7 × 13
🔵 Step 2: HCF = 13
🔵 Step 3: LCM = 2 × 7 × 13 = 182
🟡 Check: 26 × 91 = 2366; 13 × 182 = 2366
✔️ Final: HCF = 13, LCM = 182 (identity verified)
✳️ (ii) 510 and 92
🔵 Step 1: 510 = 2 × 3 × 5 × 17; 92 = 2² × 23
🔵 Step 2: HCF = 2
🔵 Step 3: LCM = 2² × 3 × 5 × 17 × 23 = 23460
🟡 Check: 510 × 92 = 46920; 2 × 23460 = 46920
✔️ Final: HCF = 2, LCM = 23460 (identity verified)
✳️ (iii) 336 and 54
🔵 Step 1: 336 = 2⁴ × 3 × 7; 54 = 2 × 3³
🔵 Step 2: HCF = 2 × 3 = 6
🔵 Step 3: LCM = 2⁴ × 3³ × 7 = 3024
🟡 Check: 336 × 54 = 18144; 6 × 3024 = 18144
✔️ Final: HCF = 6, LCM = 3024 (identity verified)
🔵 Question
3. Find the LCM and HCF of the following integers by applying the prime factorisation method.
(i) 12, 15 and 21 (ii) 17, 23 and 29 (iii) 8, 9 and 25
🟢 Answer
✳️ (i) 12, 15, 21
🔵 Step 1: 12 = 2² × 3; 15 = 3 × 5; 21 = 3 × 7
🔵 Step 2: HCF = 3
🔵 Step 3: LCM = 2² × 3 × 5 × 7 = 420
✔️ Final: HCF = 3, LCM = 420
✳️ (ii) 17, 23, 29
🔵 Step 1: All are distinct primes
🔵 Step 2: HCF = 1
🔵 Step 3: LCM = 17 × 23 × 29 = 11339
✔️ Final: HCF = 1, LCM = 11339
✳️ (iii) 8, 9, 25
🔵 Step 1: 8 = 2³; 9 = 3²; 25 = 5²
🔵 Step 2: HCF = 1
🔵 Step 3: LCM = 2³ × 3² × 5² = 1800
✔️ Final: HCF = 1, LCM = 1800
🔵 Question
4. Given that HCF (306, 657) = 9, find LCM (306, 657).
🟢 Answer
🔵 Step 1: Use identity HCF × LCM = product of numbers
🔵 Step 2: LCM = (306 × 657) ÷ 9 = 201042 ÷ 9 = 22338
✔️ Final: LCM = 22338
🔵 Question
5. Check whether 6ⁿ can end with the digit 0 for any natural number n.
🟢 Answer
🔵 Step 1: 6ⁿ = (2 × 3)ⁿ has only prime factors 2 and 3
🔵 Step 2: A number ending with 0 must be divisible by 10 = 2 × 5 (needs a factor 5)
🔵 Step 3: 6ⁿ has no factor 5
✔️ Final: 6ⁿ can never end with digit 0 for any n ∈ ℕ
🔵 Question
6. Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.
🟢 Answer
✳️ Expression 1: 7 × 11 × 13 + 13
🔵 Step 1: = 13(7 × 11 + 1) = 13(77 + 1) = 13 × 78
🔵 Step 2: Has factors 13 and 78 (> 1)
✔️ Final: Composite
✳️ Expression 2: 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 = 7! + 5
🔵 Step 1: 7! is divisible by 5 ⇒ 7! = 5k
🔵 Step 2: 7! + 5 = 5k + 5 = 5(k + 1) with k + 1 > 1
✔️ Final: Composite
🔵 Question
7. There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time. After how many minutes will they meet again at the starting point?
🟢 Answer
🔵 Step 1: Required time = LCM(18, 12)
🔵 Step 2: 18 = 2 × 3²; 12 = 2² × 3
🔵 Step 3: LCM = 2² × 3² = 4 × 9 = 36
✔️ Final: 36 minutes
Exercise 1.2
🔵 Question
Prove that √5 is irrational.
🟢 Answer
💡 Concept: Proof by contradiction using “lowest terms” and prime divisibility.
🔵 Step 1: Assume √5 is rational ⇒ √5 = a/b, where a, b ∈ ℤ, b ≠ 0, and gcd(a, b) = 1.
🔵 Step 2: Square both sides: 5 = a²/b² ⇒ a² = 5b².
🔵 Step 3: Therefore 5 ∣ a² ⇒ 5 ∣ a (since 5 is prime).
🔵 Step 4: Let a = 5k ⇒ a² = 25k².
🔵 Step 5: From a² = 5b² we get 25k² = 5b² ⇒ b² = 5k² ⇒ 5 ∣ b.
🔵 Step 6: Then 5 divides both a and b, contradicting gcd(a, b) = 1.
✔️ Final: Assumption is false ⇒ √5 is irrational.
🔵 Question
2. Prove that 3 + 2√5 is irrational.
🟢 Answer
✏️ Note: Sum of a rational and an irrational number is irrational (proved via contradiction below).
🔵 Step 1: Assume 3 + 2√5 is rational ⇒ 3 + 2√5 = r, where r ∈ ℚ.
🔵 Step 2: Rearrange: 2√5 = r − 3.
🔵 Step 3: Divide by 2 (non-zero rational): √5 = (r − 3)/2.
🔵 Step 4: Right side is rational (ℚ closed under subtraction and division by non-zero rationals).
🔵 Step 5: This implies √5 is rational, contradicting Q1.
✔️ Final: Hence 3 + 2√5 is irrational.
🔵 Question
3. Prove that the following are irrationals:
(i) 1/√2 (ii) 7√5 (iii) 6 + √2
🟢 Answer
💡 Concept: If a ≠ 0 is rational and a·α is rational, then α must be rational (contrapositive used). Also, sum of rational and irrational is irrational.
✳️ (i) 1/√2
🔵 Step 1: Suppose 1/√2 is rational ⇒ 1/√2 = q, q ∈ ℚ.
🔵 Step 2: Take reciprocal: √2 = 1/q (allowed since q ≠ 0).
🔵 Step 3: Right side is rational ⇒ √2 rational, contradiction (known irrational).
✔️ Final (i): 1/√2 is irrational.
✳️ (ii) 7√5
🔵 Step 1: Suppose 7√5 is rational ⇒ 7√5 = t, t ∈ ℚ.
🔵 Step 2: Divide by 7 (non-zero rational): √5 = t/7 (rational).
🔵 Step 3: Contradicts Q1 (√5 irrational).
✔️ Final (ii): 7√5 is irrational.
✳️ (iii) 6 + √2
🔵 Step 1: Suppose 6 + √2 is rational ⇒ 6 + √2 = s, s ∈ ℚ.
🔵 Step 2: Rearrange: √2 = s − 6 (difference of rationals ⇒ rational).
🔵 Step 3: Contradiction since √2 is irrational.
✔️ Final (iii): 6 + √2 is irrational.
————————————————————————————————————————————————————————————————————————-
OTHER IMPORTANT QUESTIONS FOR EXAMS
🔵 Section A (1 mark each — MCQ, )
🔵 Question
Q1. If HCF(306, 657) is found using Euclid’s Division Lemma, the final HCF is:
🟣 Options:
• (A) 3 • (B) 9 • (C) 17 • (D) 27
🟢 Answer
✳️ ➤ Euclid steps (sketch): 657 = 306×2 + 45; 306 = 45×6 + 36; 45 = 36×1 + 9; 36 = 9×4 + 0 ⇒ HCF = 9
✔️ Correct option: (B) 9
🔵 Question
Q2. The prime factorisation of 98 is:
🟣 Options:
• (A) 2×7² • (B) 2²×7 • (C) 2×7×7×7 • (D) 2×5×7
🟢 Answer
✳️ ➤ 98 = 2×49 = 2×7²
✔️ Correct option: (A) 2×7²
🔵 Question
Q3. The decimal expansion of the rational number 27/125 will be:
🟣 Options:
• (A) Terminating • (B) Non-terminating recurring • (C) Non-terminating non-recurring • (D) Not a rational number
🟢 Answer
✳️ ➤ 125 = 5³ ⇒ denominator of form 2^m5^n ⇒ terminating
✔️ Correct option: (A) Terminating
🔵 Question
Q4. Which of the following is irrational?
🟣 Options:
• (A) √49 • (B) 3/11 • (C) 0.̅6 (recurring) • (D) √2
🟢 Answer
✳️ ➤ √49 = 7 (rational), 3/11 rational, recurring decimal rational, √2 irrational
✔️ Correct option: (D) √2
🔵 Question
Q5. If p and q are coprime and q has prime factors only 2 and 5, then p/q has:
🟣 Options:
• (A) A non-terminating non-recurring decimal
• (B) A terminating decimal
• (C) A recurring decimal
• (D) Not defined
🟢 Answer
✳️ ➤ Denominator of form 2m5n ⇒ terminating
✔️ Correct option: (B) A terminating decimal
🔵 Question
Q6. LCM(24, 90) equals:
🟣 Options:
• (A) 180 • (B) 360 • (C) 720 • (D) 90
🟢 Answer
✳️ ➤ 24 = 2³×3; 90 = 2×3²×5 ⇒ LCM = 2³×3²×5 = 8×9×5 = 360
✔️ Correct option: (B) 360
🟢 Section B (2 marks each — Short Answer-I)
🟢 Question
Q7. Use Euclid’s Division Lemma to find HCF(255, 867).
🔴 Answer
✳️ ➤ Division steps:
➡ 867 = 255×3 + 102
➡ 255 = 102×2 + 51
➡ 102 = 51×2 + 0
✔️ Final: HCF = 51
🟢 Question
Q8. Show that the product of any three consecutive integers is divisible by 6.
🔴 Answer
✳️ ➤ Let integers be n, n+1, n+2.
✳️ ➤ Even factor: Among three consecutive numbers, one is even ⇒ factor 2 divides product.
✳️ ➤ Multiple of 3: One of n, n+1, n+2 ≡ 0 (mod 3) ⇒ factor 3 divides product.
✔️ Final: Product divisible by 2×3 = 6.
🟢 Question
Q9. Without actual division, state whether 77/2⁵×5² has a terminating decimal expansion.
🔴 Answer
✳️ ➤ Denominator = 2⁵×5² = (2m5n) form.
✔️ Final: Terminating decimal expansion.
🟢 Question
Q10. Express 3/40 in the form p/2m5n and write its decimal expansion type.
🔴 Answer
✳️ ➤ 40 = 2³×5 ⇒ 3/40 = 3/(2³×5¹).
✔️ Final: Denominator 2^m5^n ⇒ terminating; value = 0.075.
🟢 Question
Q11. Find HCF and LCM of 72 and 120 using prime factorisation, and verify HCF×LCM = product of numbers.
🔴 Answer
✳️ ➤ 72 = 2³×3²; 120 = 2³×3×5.
✳️ ➤ HCF: 2³×3¹ = 8×3 = 24.
✳️ ➤ LCM: 2³×3²×5 = 8×9×5 = 360.
✳️ ➤ Verify: HCF×LCM = 24×360 = 8640; product = 72×120 = 8640.
✔️ Final: HCF = 24, LCM = 360, identity verified.
🟢 Question
Q12. Prove that √5 is irrational.
🔴 Answer
✳️ ➤ Assume contrary: √5 = a/b in lowest terms, a, b ∈ ℤ, b ≠ 0.
✳️ ➤ Square: 5 = a²/b² ⇒ a² = 5b² ⇒ a² divisible by 5 ⇒ a divisible by 5 ⇒ let a = 5k.
✳️ ➤ Substitute: a² = 25k² = 5b² ⇒ b² = 5k² ⇒ b divisible by 5.
✳️ ➤ Contradiction: a, b both divisible by 5, not in lowest terms.
✔️ Final: Assumption false ⇒ √5 irrational.
🟡 Section C (3 marks each — Short Answer-II with internal choices)
🔵 Question 13
Find HCF of 126 and 405 using Euclid’s Division Lemma.
🟢 Answer
✳️ ➤ 405 = 126×3 + 27
✳️ ➤ 126 = 27×4 + 18
✳️ ➤ 27 = 18×1 + 9
✳️ ➤ 18 = 9×2 + 0
✔ Final: HCF = 9
🔵 Question 14
Show that 15×7×10×21 + 35 is divisible by 35.
🟢 Answer
✳️ ➤ Factorise: 15 = 3×5, 7 = 7, 10 = 2×5, 21 = 3×7.
✳️ ➤ Product 15×7×10×21 = (3×5)(7)(2×5)(3×7) = 3²×5²×7²×2.
✳️ ➤ Clearly divisible by 35 = 5×7. Adding 35 keeps divisibility.
✔ Final: Divisible by 35.
🔵 Question 15
Prove that √7 is irrational.
🟢 Answer
✳️ ➤ Assume √7 = a/b in lowest terms, b≠0.
✳️ ➤ Square: 7 = a²/b² ⇒ a² = 7b².
✳️ ➤ a divisible by 7 ⇒ let a=7k ⇒ a²=49k²=7b² ⇒ b²=7k² ⇒ b divisible by 7.
✳️ ➤ Both divisible by 7 ⇒ contradiction.
✔ Final: √7 is irrational.
🔵 Question 16
OR
Show that there are infinitely many primes.
🟢 Answer
✳️ ➤ Suppose finitely many primes: p₁,p₂,…,pₙ.
✳️ ➤ Consider N = p₁p₂…pₙ + 1.
✳️ ➤ N not divisible by any pᵢ (remainder 1).
✳️ ➤ Either N is prime or has prime factors not in list ⇒ contradiction.
✔ Final: Infinitely many primes exist.
🔵 Question 17
Find LCM and HCF of 420 and 130 using prime factorisation.
🟢 Answer
✳️ ➤ 420 = 2²×3×5×7.
✳️ ➤ 130 = 2×5×13.
✳️ ➤ HCF = 2×5 = 10.
✳️ ➤ LCM = 2²×3×5×7×13 = 4×3×5×7×13 = 5460.
✳️ ➤ Verify: 10×5460 = 54,600 = 420×130 ✔.
✔ Final: HCF=10, LCM=5460.
🔵 Question 18
Find the HCF of 867 and 255 using Euclid’s algorithm and verify HCF×LCM = product of numbers.
🟢 Answer
✳️ ➤ 867 = 255×3 + 102.
✳️ ➤ 255 = 102×2 + 51.
✳️ ➤ 102 = 51×2 + 0 ⇒ HCF = 51.
✳️ ➤ LCM = (867×255)/51 = 4335.
✳️ ➤ Check: 51×4335 = 221,085 = 867×255.
✔ Final: HCF=51, LCM=4335.
🔵 Question 19
Show that 12ⁿ − 1 is divisible by 11 for all natural numbers n.
🟢 Answer
✳️ ➤ Use induction base: n=1 ⇒12−1=11 divisible by 11.
✳️ ➤ Assume true for n=k ⇒12ᵏ−1 divisible by11 ⇒12ᵏ=11m+1.
✳️ ➤ For n=k+1:12ᵏ⁺¹−1=12·12ᵏ−1=12(11m+1)−1=132m+12−1=132m+11=11(12m+1).
✔ Final: Divisible by 11 for all n.
🔵 Question 20
Find the HCF of 396 and 264 using Euclid’s algorithm.
🟢 Answer
✳️ ➤ 396 = 264×1 + 132.
✳️ ➤ 264 = 132×2 + 0.
✔ Final: HCF = 132.
🔵 Question 21
Show that one and only one of n, n+2, n+4 is divisible by 3.
🟢 Answer
✳️ ➤ Any integer ≡0,1,2 (mod 3).
🟢 Case1: n≡0 ⇒ divisible. Then n+2≡2, n+4≡1 ⇒ not divisible.
🟢 Case2: n≡1 ⇒ n+2≡0 divisible, others not.
🟢 Case3: n≡2 ⇒ n+4≡0 divisible, others not.
✔ Final: Exactly one divisible by 3.
🔵 Question 22
Use Euclid’s Division Lemma to show that the square of any positive integer is of the form 3m or 3m+1 for some integer m.
🟢 Answer
✳️ ➤ Let integer n=3q or3q+1 or3q+2.
🟢 Case1: n=3q ⇒n²=9q²=3(3q²)=3m.
🟢 Case2: n=3q+1 ⇒n²=9q²+6q+1=3(3q²+2q)+1=3m+1.
🟢 Case3: n=3q+2 ⇒n²=9q²+12q+4=3(3q²+4q+1)+1=3m+1.
✔ Final: n² is 3m or 3m+1.
🔴 Section D (4 marks each — Long Answer with internal choices)
🔵 Question 23
Find the LCM and HCF of 510 and 92 and verify HCF × LCM = product of the numbers.
🟢 Answer
✳️ ➤ 510 = 92×5 + 50
✳️ ➤ 92 = 50×1 + 42
✳️ ➤ 50 = 42×1 + 8
✳️ ➤ 42 = 8×5 + 2
✳️ ➤ 8 = 2×4 + 0 ⇒ HCF = 2
✳️ ➤ LCM = (510×92)/2 = 23460
✳️ ➤ Verify: 2×23460 = 510×92 = 46920 ✔
✔ Final: HCF=2, LCM=23460
🔵 Question 24
Prove that there are infinitely many positive integers divisible by 5.
🟢 Answer
✳️ ➤ Multiples of 5: 5, 10, 15,…,5n.
✳️ ➤ Suppose only finitely many. Take number =5k where k is beyond list ⇒ contradiction.
✔ Final: Infinitely many integers divisible by 5 exist.
🔵 Question 25
Find the HCF of 336 and 54 using Euclid’s algorithm. Also find integers x and y such that HCF = 336x + 54y.
🟢 Answer
✳️ ➤ 336 = 54×6 + 12
✳️ ➤ 54 = 12×4 + 6
✳️ ➤ 12 = 6×2 + 0 ⇒ HCF = 6
✳️ ➤ Back-substitute: 6 = 54 − 12×4
✳️ ➤ 12 = 336 − 54×6 ⇒6=54−4(336−54×6)=54−4×336+24×54=25×54−4×336
✔ Final: HCF=6 = 25×54 − 4×336
🔵 Question 26
OR
Prove that there are infinitely many primes congruent to 1 mod 4.
🟢 Answer
✳️ ➤ Suppose finitely many primes ≡1 mod4: p₁,…,pₙ.
✳️ ➤ Consider N = 4(p₁p₂…pₙ)² + 1.
✳️ ➤ N ≡1 mod4 and not divisible by any pᵢ.
✳️ ➤ Contradiction ⇒ infinitely many such primes.
✔ Final: Infinitely many primes ≡1 mod4
🔵 Question 27
Show that every positive even integer is of the form 6q, 6q+2, or 6q+4 for some integer q.
🟢 Answer
✳️ ➤ Let n be even ⇒ n=2k.
✳️ ➤ Write k=3q or3q+1 or3q+2.
➡ Case1: k=3q ⇒ n=6q.
➡ Case2: k=3q+1 ⇒ n=6q+2.
➡ Case3: k=3q+2 ⇒ n=6q+4.
✔ Final: Proved
🔵 Question 28
The decimal expansion of a rational number terminates after 3 decimal places. What can you say about the prime factors of its denominator?
🟢 Answer
✳️ ➤ A rational number terminates if denominator in lowest form =2m5n
✳️ ➤ Terminating after 3 decimals ⇒ denominator divides 10³=1000=2³×5³.
✔ Final: Prime factors only 2 and 5
🔵 Question 29
Find the HCF and LCM of 144 and 180 by prime factorisation method and verify HCF × LCM = product of numbers.
🟢 Answer
✳️ ➤ 144=2⁴×3², 180=2²×3²×5.
✳️ ➤ HCF=2²×3²=4×9=36.
✳️ ➤ LCM=2⁴×3²×5=16×9×5=720.
✳️ ➤ Verify:36×720=25920=144×180 ✔
✔ Final: HCF=36, LCM=720
🔵 Question 30
Show that √3 is irrational.
🟢 Answer
✳️ ➤ Assume √3=a/b in lowest terms.
✳️ ➤ Square:3=a²/b²⇒a²=3b²⇒a divisible by3⇒a=3k.
✳️ ➤ Substitute:9k²=3b²⇒b²=3k²⇒b divisible by3.
✳️ ➤ Both divisible by3⇒contradiction.
✔ Final: √3 is irrational
————————————————————————————————————————————————————————————————————————————
MIND MAP

——————————————————————————————————————————————————————————————————————————–
