Class 12 : Physics (English) – Chapter 10: Wave Optics

Posted by

On June 25, 2025

EXPLANATION & SUMMARY

Introduction to Wave Optics
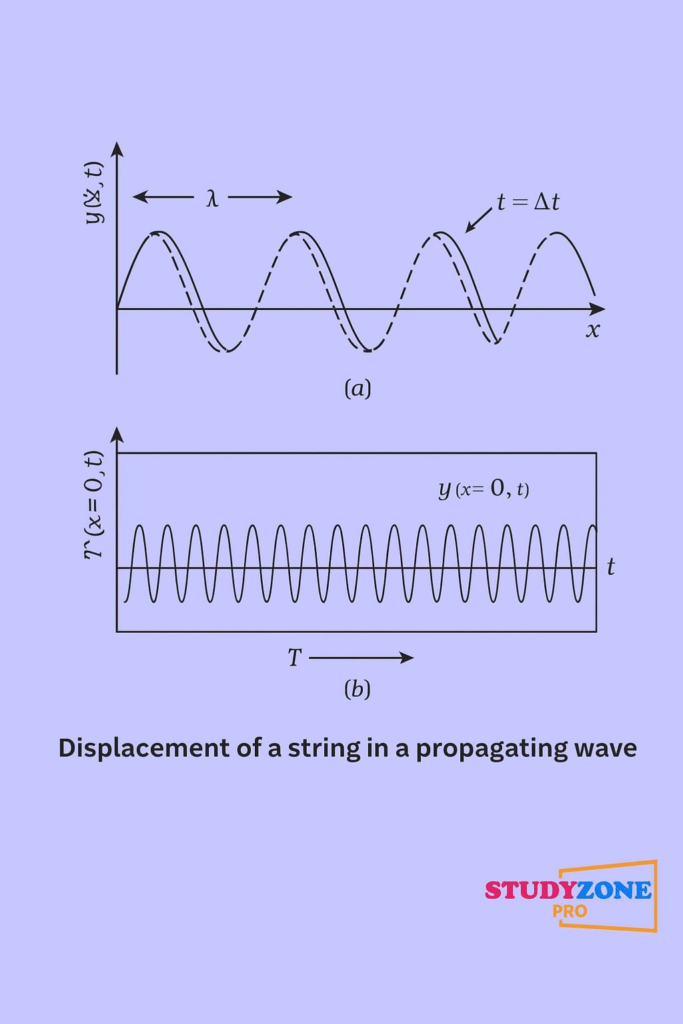
Wave Optics deals with the wave nature of light and phenomena like interference, diffraction, and polarization which cannot be explained using ray optics alone. While ray optics treats light as straight-line rays, wave optics explains the behavior of light as a wave, especially its ability to bend, combine, and interfere. The foundation of wave optics lies in Huygens’ Principle and the wave theory of light proposed by Christiaan Huygens.

Huygens’ Principle
Huygens proposed that every point on a wavefront acts as a source of secondary spherical wavelets, and the new wavefront is the envelope of these wavelets. Using this principle, one can predict the future position of a wavefront and analyze the propagation of light.
There are two important laws derived from Huygens’ principle:
Law of Reflection: The angle of incidence equals the angle of reflection.
Law of Refraction (Snell’s Law): The ratio of sines of the angle of incidence and refraction is equal to the ratio of velocities (or refractive indices) of the two media.

Refraction and Reflection using Huygens’ Principle
By applying Huygens’ construction to a wavefront approaching a plane boundary, the laws of reflection and refraction can be geometrically derived. This confirms that the wave theory agrees with ray optics for phenomena involving plane surfaces.

The Doppler Effect in Light
Though primarily a concept in sound waves, the Doppler effect is applicable to light waves too. When the source or observer is moving, the apparent frequency of light changes, leading to redshift or blueshift observed in astronomy.

Coherent and Incoherent Sources
For observable interference, two sources of light must be coherent — i.e., have constant phase difference and the same frequency. Ordinary sources like bulbs are incoherent as their emitted waves have random phases.
Examples of coherent sources:
Two slits illuminated by the same monochromatic source (as in Young’s experiment).
Laser beams.

Interference of Light
When two light waves superpose, the resultant intensity at any point depends on the phase difference between them.
Constructive Interference occurs when the waves are in phase (phase difference = 0, 2π, etc.) and the intensities add up.
Destructive Interference occurs when the waves are out of phase by π, 3π, etc., and cancel each other.
The intensity at any point on the screen is given by:
I = I₁ + I₂ + 2√(I₁I₂) cos(φ)
Where φ is the phase difference.

Young’s Double Slit Experiment (YDSE)
This experiment demonstrates the interference of light.
A monochromatic source illuminates two narrow slits S₁ and S₂.
The light waves from S₁ and S₂ interfere on a screen placed at distance D.
Bright and dark fringes appear due to constructive and destructive interference.
Let d be the distance between the slits, λ the wavelength of light, and x the distance from the central maximum on the screen.

The path difference is:
Δ = (d × x)/D
The condition for:
Constructive interference: Δ = nλ
Destructive interference: Δ = (2n + 1)λ/2
The fringe width (distance between two successive bright or dark fringes) is:
β = λD/d
Fringe width depends on:
Wavelength (λ)
Distance to screen (D)
Distance between slits (d)

Intensity Distribution
The maximum intensity is at the central bright fringe. As one moves away from the center, the intensity gradually decreases. This sinusoidal variation of intensity supports the wave nature of light.

Diffraction of Light
Diffraction refers to the bending and spreading of light waves when they encounter an obstacle or slit comparable in size to the wavelength.
There are two types:
Fresnel Diffraction – Source and screen are at finite distances.
Fraunhofer Diffraction – Source and screen are at infinite distances (or made parallel using lenses).
In single slit diffraction, the central maximum is the brightest and twice as wide as the side fringes.
Condition for minima:
a sinθ = nλ
Where:
a = width of slit
θ = angle of diffraction
λ = wavelength
n = ±1, ±2, …

Interference vs Diffraction
Interference occurs between two (or more) coherent sources.
Diffraction results from the superposition of waves from different parts of the same wavefront.
Fringe width is almost constant in interference but varies in diffraction.

Resolving Power of Optical Instruments
Resolution is the ability to distinguish two close objects. It is limited by diffraction effects.
Rayleigh’s Criterion: Two point sources are just resolved if the principal maximum of one image coincides with the first minimum of the other.
For telescope:
θ = 1.22 λ/D
Where D is the aperture diameter.
For microscope:
d = 0.61 λ/μ sinθ
Where d is the minimum distance resolvable, μ is refractive index, and θ is angular aperture.

Polarization of Light
Light waves are transverse electromagnetic waves. In unpolarized light, the electric vector vibrates in all directions perpendicular to the direction of propagation.
Polarized Light: Vibration is restricted to one direction only.
Methods of polarization:
By reflection (Brewster’s law): Light reflected at a certain angle (Brewster angle) becomes completely polarized. tan i = n (i = polarizing angle, n = refractive index)
By refraction
By scattering
By using polarizing materials (Polaroids)

Uses of Polarized Light
Sunglasses to reduce glare
Stress analysis in materials
3D movies
Optical instruments like microscopes and cameras

Wave Nature of Light Explained
Wave optics successfully explains:
Interference (Young’s experiment)
Diffraction (single slit and grating)
Polarization (not explainable by particle theory)

✍ SUMMARY (Approx. 300 Words)
Wave Optics deals with the wave nature of light and explains phenomena like interference, diffraction, and polarization.
Huygens’ Principle states that every point on a wavefront is a source of secondary wavelets. This principle helps derive laws of reflection and refraction.
Interference is the superposition of two coherent waves. Constructive interference gives bright fringes (path difference = nλ) and destructive interference gives dark fringes (path difference = (2n + 1)λ/2).

Young’s Double Slit Experiment (YDSE) proves the wave nature of light. Fringe width is given by β = λD/d.
Diffraction is the bending of light around obstacles or through slits. Single slit diffraction produces a central maximum that is widest and brightest.
Rayleigh’s Criterion defines the limit of resolution of optical instruments. Resolution improves with smaller wavelength and larger aperture.

Polarization is a unique property of transverse waves. Light can be polarized by reflection, refraction, or using Polaroids.
Brewster’s Law gives the polarizing angle: tan i = n.
Wave optics explains interference, diffraction, and polarization—all of which support the wave nature of light, in contrast to the particle model.

—————————————————————————————————————————————————————————————————————————————-

QUESTIONS FROM TEXTBOOK

Question 10.1
Monochromatic light of wavelength 589 nm is incident from air on a water surface. What are the wavelength, frequency and speed of
(a) reflected, and
(b) refracted light?
(Refractive index of water is 1.33)
Answer:
Given:
Wavelength in air, λ = 589 nm = 589 × 10⁻⁹ m
Speed of light in vacuum (air), c = 3 × 10⁸ m/s
Refractive index of water, μ = 1.33
(a) Reflected light
The reflected light remains in air. Hence:
Speed = c = 3 × 10⁸ m/s
Wavelength = 589 nm
Frequency = c / λ
= (3 × 10⁸) / (589 × 10⁻⁹)
≈ 5.09 × 10¹⁴ Hz
(b) Refracted light
Speed in water, v = c / μ = (3 × 10⁸) / 1.33 ≈ 2.26 × 10⁸ m/s
Frequency remains the same as in air: 5.09 × 10¹⁴ Hz
Wavelength in water, λ’ = v / f = (2.26 × 10⁸) / (5.09 × 10¹⁴) ≈ 444 × 10⁻⁹ m = 444 nm

Question 10.2
What is the shape of the wavefront in each of the following cases:
(a) Light diverging from a point source.
(b) Light emerging out of a convex lens when a point source is placed at its focus.
(c) The portion of the wavefront of light from a distant star intercepted by the Earth.
Answer:
(a) Spherical wavefront – Light diverging from a point source spreads out in all directions, forming spherical wavefronts.
(b) Plane wavefront – When a point source is at the focus of a convex lens, the light rays emerge parallel and form a plane wavefront.
(c) Plane wavefront – Light from a distant star has wavefronts that are practically planar by the time they reach Earth, due to the large distance.

Question 10.3
(a) The refractive index of glass is 1.5. What is the speed of light in glass?
(Speed of light in vacuum is 3.0 × 10⁸ m/s)
(b) Is the speed of light in glass independent of the colour of light? If not, which of the two colours – red and violet – travels slower in a glass prism?
Answer:
(a)
Refractive index, μ = c / v
⇒ v = c / μ = (3.0 × 10⁸) / 1.5 = 2.0 × 10⁸ m/s
(b)
No, the speed of light in glass is not independent of the colour.
Violet light travels slower than red light in a glass prism because it has a higher refractive index (greater deviation), hence lower speed.

Question 10.4
In a Young’s double-slit experiment, the slits are separated by 0.28 mm and the screen is placed 1.4 m away. The distance between the central bright fringe and the fourth bright fringe is measured to be 1.2 cm. Determine the wavelength of light used in the experiment.
Answer:
Given:
Distance between slits, d = 0.28 mm = 0.28 × 10⁻³ m
Distance to screen, D = 1.4 m
Distance to 4th bright fringe, y = 1.2 cm = 1.2 × 10⁻² m
Fringe number, n = 4
Fringe position formula:
y = nλD / d
⇒ λ = yd / (nD)
= (1.2 × 10⁻² × 0.28 × 10⁻³) / (4 × 1.4)
= (3.36 × 10⁻⁶) / 5.6
≈ 6 × 10⁻⁷ m = 600 nm

Question 10.5
In Young’s double-slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ is K units. What is the intensity of light at a point where path difference is λ/3?
Answer:
Intensity in interference pattern is given by:
I = I₀ cos²(φ/2), where φ = phase difference = (2π/λ) × path difference
For path difference = λ:
φ = 2π ⇒ I = I₀ cos²(π) = I₀ × 0 = 0
But given intensity is K, so we treat K as the reference.
Now, for path difference = λ/3:
φ = (2π/λ) × (λ/3) = 2π/3
So,
I = K × cos²(π/3) = K × (1/2)² = K/4
Answer: Intensity = K/4 units

Question 10.6
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
(a) Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
(b) What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide?
Answer:
(a)
Fringe position: y = nλD / d
Let n = 3, λ = 650 nm = 650 × 10⁻⁹ m
Then y = (3 × 650 × 10⁻⁹ × D) / d
⇒ y = (1950 × 10⁻⁹ × D) / d
Answer: The distance is (1950 × 10⁻⁹ × D) / d meters
(Numerical value depends on D and d which are not provided.)
(b)
To find the least distance where bright fringes due to both wavelengths coincide, we find the LCM of wavelengths.
LCM of 650 nm and 520 nm = LCM of 650 and 520 = 3380 nm
Answer: Least distance from central maximum = (LCM × D) / d
= (3380 × 10⁻⁹ × D) / d meters
(Numerical value depends on D and d)
—Let’s assume specific values for D = 1.0 m and d = 0.2 mm = 0.2 × 10⁻³ m, which are typical in Young’s double-slit experiments.

Question 10.6 (continued with values):
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
(a) Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
(b) What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide?
—assume :
If Given:
λ₁ = 650 nm = 650 × 10⁻⁹ m
λ₂ = 520 nm = 520 × 10⁻⁹ m
D = 1.0 m
d = 0.2 mm = 0.2 × 10⁻³ m
n = 3

(a) Distance of 3rd bright fringe for λ = 650 nm:
Using the formula:
y = nλD / d
= (3 × 650 × 10⁻⁹ × 1.0) / (0.2 × 10⁻³)
= (1950 × 10⁻⁹) / (0.2 × 10⁻³)
= (1950 / 0.2) × 10⁻⁶
= 9750 × 10⁻⁶ m = 9.75 mm

(b) Least distance from central maximum where both fringes coincide:
First, find LCM of 650 nm and 520 nm:
LCM (650, 520) = 3380 nm = 3380 × 10⁻⁹ m
Then,
y = LCM × D / d
= (3380 × 10⁻⁹ × 1.0) / (0.2 × 10⁻³)
= (3380 / 0.2) × 10⁻⁶
= 16900 × 10⁻⁶ m = 16.9 mm

Final Answers:
(a) 9.75 mm
(b) 16.9 mm

——————————————————————————————————————————————————————————————————————————————

NEET QUESTIONS FROM THIS LESSON

Q1. A parallel beam of light of wavelength 600 nm is incident normally on a slit of width 1.5 mm. The angular width of the central maxima in the diffraction pattern is
(A) 0.24 rad
(B) 0.8 rad
(C) 0.16 rad
(D) 0.4 rad
Answer: (A)
Year: 2025 | Set: M3

Q2. In a single slit diffraction experiment, the width of the slit is made double. The width of the central maximum will become
(A) Half
(B) Double
(C) Four times
(D) One-fourth
Answer: (A)
Year: 2025 | Set: Q3

Q3. Two beams of light having intensities I and 4I interfere to produce a fringe pattern. The ratio of the maximum to the minimum intensity in the fringe pattern is
(A) 25:1
(B) 9:1
(C) 5:1
(D) 4:1
Answer: (B)
Year: 2024 | Set: Z

Q4. Which of the following phenomena shows the particle nature of light?
(A) Diffraction
(B) Polarisation
(C) Photoelectric effect
(D) Interference
Answer: (C)
Year: 2024 | Set: X

Q5. In Young’s double slit experiment, the two slits are 1 mm apart and the screen is placed 1.25 m away. The distance between the central bright fringe and the fourth bright fringe is 1.2 cm. The wavelength of light used is
(A) 480 nm
(B) 600 nm
(C) 500 nm
(D) 640 nm
Answer: (B)
Year: 2023 | Set: Q2

Q6. The angular width of the central maximum in a single slit diffraction pattern is 60°. The width of the slit is 1 µm. The wavelength of light is
(A) 1000 nm
(B) 500 nm
(C) 750 nm
(D) 1500 nm
Answer: (A)
Year: 2023 | Set: M1

Q7. Two light waves emerging from slits in Young’s experiment are coherent if
(A) They have the same intensity
(B) They are both polarized
(C) They have the same phase or constant phase difference
(D) They have equal amplitudes
Answer: (C)
Year: 2022 | Set: S1

Q8. When the width of the slit is increased in a single slit diffraction experiment, the central maximum becomes
(A) Broader
(B) Narrower
(C) Unchanged
(D) Brighter
Answer: (B)
Year: 2022 | Set: Z

Q9. In Young’s double slit experiment, if the distance between slits is halved, fringe width will
(A) Be halved
(B) Remain unchanged
(C) Be doubled
(D) Become four times
Answer: (C)
Year: 2021 | Set: R2

Q10. Two coherent sources of intensities I and 4I are used in Young’s double slit experiment. The visibility of fringes is
(A) 1
(B) 0.6
(C) 0.8
(D) 0.4
Answer: (B)
Year: 2021 | Set: P2

Q11. In the interference pattern observed in Young’s double slit experiment, if the distance between the screen and the slits is doubled, then the fringe width
(A) Becomes half
(B) Remains the same
(C) Doubles
(D) Becomes four times
Answer: (C)
Year: 2020 | Set: Z

Q12. When light of wavelength λ passes through a single slit of width a, the angular position of the first minimum on either side of central maximum is
(A) λ/a
(B) a/λ
(C) λ/2a
(D) 2λ/a
Answer: (A)
Year: 2020 | Set: S2

Q13. If the Young’s double slit experiment is performed with white light, then
(A) All bright fringes are white
(B) Central fringe is white and all others are coloured
(C) All dark fringes are black
(D) All fringes are coloured
Answer: (B)
Year: 2019 | Set: N2

Q14. In a single slit diffraction, the width of the central maximum is
(A) Equal to the slit width
(B) Inversely proportional to slit width
(C) Directly proportional to slit width
(D) Independent of slit width
Answer: (B)
Year: 2019 | Set: O1

Q15. Which of the following can be polarized?
(A) Sound wave
(B) Longitudinal wave
(C) Transverse wave
(D) Shock wave
Answer: (C)
Year: 2018 | Set: Q1

Q16. Polarisation is a phenomenon shown by
(A) Transverse waves
(B) Longitudinal waves
(C) All types of mechanical waves
(D) Sound waves only
Answer: (A)
Year: 2018 | Set: W

Q17. In Young’s double slit experiment, the fringe width is 0.2 cm. If the whole apparatus is immersed in water (µ = 4/3), the fringe width becomes
(A) 0.15 cm
(B) 0.20 cm
(C) 0.30 cm
(D) 0.133 cm
Answer: (D)
Year: 2017 | Set: Z

Q18. In a diffraction pattern due to a single slit, the width of the central maximum is 4 mm. When the slit width is doubled, the width of central maximum becomes
(A) 2 mm
(B) 4 mm
(C) 8 mm
(D) 1 mm
Answer: (A)
Year: 2017 | Set: Y

Q19. In a single slit diffraction experiment, the first minimum is at an angle θ. If the wavelength of light is doubled and slit width is also doubled, the angle of minimum
(A) Remains the same
(B) Doubles
(C) Halves
(D) Becomes four times
Answer: (A)
Year: 2016 | Set: A

Q20. Two light sources are said to be coherent when they emit
(A) Radiations of same frequency
(B) Continuous radiations
(C) Radiations of same amplitude
(D) Waves with constant phase difference
Answer: (D)
Year: 2016 | Set: X

Q21. Diffraction of light is evidence of
(A) Particle nature of light
(B) Transverse nature of light
(C) Wave nature of light
(D) Electromagnetic nature of light
Answer: (C)
Year: 2015 | Set: C

Q22. The ratio of intensities at maxima and minima in an interference pattern is 36:4. The ratio of amplitudes of the two interfering waves is
(A) 3:1
(B) 4:1
(C) 5:1
(D) 6:1
Answer: (C)
Year: 2015 | Set: B

Q23. Interference fringes are not observed in white light because
(A) It has low intensity
(B) White light is a mixture of many wavelengths
(C) It has low speed
(D) It has high frequency
Answer: (B)
Year: 2014 | Set: M

Q24. The condition for constructive interference is
(A) Path difference = nλ
(B) Path difference = (2n+1)λ/2
(C) Phase difference = π
(D) Path difference = λ/2
Answer: (A)
Year: 2014 | Set: N

Q25. In a single slit diffraction pattern, the first minimum occurs at angle θ given by
(A) sinθ = λ/a
(B) sinθ = a/λ
(C) sinθ = λ/2a
(D) sinθ = 2λ/a
Answer: (A)
Year: 2013 | Set: K

Q26. The central maximum in a single slit diffraction pattern is
(A) Brighter and narrower than others
(B) Brighter and wider than others
(C) Of same width and intensity
(D) Dark
Answer: (B)
Year: 2013 | Set: P

Q27. The distance between two consecutive bright fringes in Young’s double slit experiment is called
(A) Amplitude
(B) Wavelength
(C) Fringe width
(D) Path difference
Answer: (C)
Year: 2012 | Set: Y

Q28. The angular width of central maximum in diffraction pattern increases when
(A) Wavelength decreases
(B) Slit width increases
(C) Slit width decreases
(D) None of these
Answer: (C)
Year: 2012 | Set: A

Q29. In Young’s experiment, if the fringe width is β, the distance between the slits is d and the screen is at distance D, then wavelength is given by
(A) βD/d
(B) dD/β
(C) βd/D
(D) D/βd
Answer: (A)
Year: 2011 | Set: Q

Q30. Which of the following phenomena cannot be explained by wave theory of light?
(A) Diffraction
(B) Interference
(C) Polarisation
(D) Photoelectric effect
Answer: (D)
Year: 2011 | Set: S

Q31. When two waves of same frequency and constant phase difference superpose, the resultant intensity varies as
(A) Square of amplitude
(B) Sum of amplitudes
(C) Product of amplitudes
(D) Difference of amplitudes
Answer: (A)
Year: 2010 | Set: B

Q32. Which of the following is not an application of polarization?
(A) Sunglasses
(B) Optical filters
(C) Interference
(D) 3D glasses
Answer: (C)
Year: 2010 | Set: M

Q33. Which principle is used to explain diffraction?
(A) Newton’s Laws
(B) Snell’s Law
(C) Huygens’ Principle
(D) Doppler Effect
Answer: (C)
Year: 2009 | Set: A

Q34. In Young’s double slit experiment, bright fringes appear due to
(A) Destructive interference
(B) Constructive interference
(C) Diffraction
(D) Refraction
Answer: (B)

Q35. The phenomenon of interference is a direct consequence of
(A) Reflection
(B) Refraction
(C) Superposition principle
(D) Diffraction
Answer: (C)
Year: 2008 | Set: W

Q36. The wavelength of sodium light in air is 5890 Å. What is its wavelength in water (μ = 4/3)?
(A) 4417.5 Å
(B) 5890 Å
(C) 7853.3 Å
(D) 3930 Å
Answer: (A)
Year: 2008 | Set: Y

Q37. The width of the central maximum in a single slit diffraction pattern is
(A) Inversely proportional to the slit width
(B) Directly proportional to the slit width
(C) Inversely proportional to the square of the slit width
(D) Independent of the slit width
Answer: (A)
Year: 2007 | Set: M

Q38. The ratio of intensities at two points in an interference pattern is 4:1. What is the ratio of the amplitudes?
(A) 2:1
(B) 4:1
(C) 16:1
(D) 1:2
Answer: (A)
Year: 2007 | Set: N

Q39. In Young’s double slit experiment, the path difference between the two waves is zero. The interference is
(A) Constructive
(B) Destructive
(C) Zero
(D) Maximum destructive
Answer: (A)
Year: 2006 | Set: A

Q40. When unpolarized light is incident on a polaroid, the intensity of transmitted light is reduced by
(A) Half
(B) One-fourth
(C) One-third
(D) Two-thirds
Answer: (A)
Year: 2006 | Set: X

Q41. In a diffraction pattern due to a single slit, if the width of the slit is made half, the width of the central maximum will
(A) Double
(B) Remain same
(C) Become half
(D) Become four times
Answer: (A)
Year: 2005 | Set: Y

Q42. In Young’s experiment, the maximum intensity is I. What will be the resultant intensity at a point where the path difference is λ/3?
(A) I
(B) I/4
(C) I/2
(D) 3I/4
Answer: (D)
Year: 2005 | Set: W

Q43. The Brewster angle for light incident from air to glass surface (n = 1.5) is
(A) tan⁻¹(1.5)
(B) sin⁻¹(1.5)
(C) 45°
(D) 90°
Answer: (A)
Year: 2004 | Set: Z

Q44. In a diffraction experiment with a single slit, light of wavelength 5000 Å is used. If the angular position of the first minimum is 30°, the width of the slit is
(A) 10⁻⁵ m
(B) 10⁻⁶ m
(C) 10⁻⁴ m
(D) 10⁻³ m
Answer: (B)
Year: 2004 | Set: P

Q45. Two waves of the same frequency and constant phase difference interfere. The resulting pattern is
(A) Stationary
(B) Traveling
(C) Oscillating
(D) Reflected
Answer: (A)
Year: 2003 | Set: A

Q46. The fringe width in Young’s double slit experiment is 0.2 cm. If the whole apparatus is placed in a medium of refractive index 1.5, the fringe width becomes
(A) 0.1 cm
(B) 0.15 cm
(C) 0.3 cm
(D) 0.4 cm
Answer: (B)
Year: 2003 | Set: B

Q47. If one of the slits in Young’s experiment is closed, then
(A) No interference pattern is observed
(B) Bright and dark fringes become broader
(C) Central maximum becomes more intense
(D) Diffraction pattern appears
Answer: (D)
Year: 2002 | Set: X

Q48. A beam of unpolarized light of intensity I is passed through a polaroid. The intensity of the light passing through the polaroid is
(A) I
(B) I/2
(C) 2I
(D) Zero
Answer: (B)
Year: 2002 | Set: Y

Q49. Light shows wave nature in
(A) Photoelectric effect
(B) Compton effect
(C) Interference
(D) Electron emission
Answer: (C)
Year: 2001 | Set: Z

Q50. In Young’s double slit experiment, the distance between the screen and the plane of the slits is doubled. The fringe width will
(A) Increase
(B) Decrease
(C) Remain the same
(D) Become half
Answer: (A)
Year: 2001 | Set: A

Q51. A polarized light is incident on a polaroid. If the intensity of incident light is I, the intensity of light transmitted when the polaroid is at 60° is
(A) I
(B) I/2
(C) I/4
(D) I cos²60°
Answer: (D)
Year: 2025 | Set: R1

Q52. In a single slit diffraction experiment, the first minima occurs at θ = 30°, wavelength = 600 nm. The width of the slit is
(A) 1.2 × 10⁻⁶ m
(B) 6 × 10⁻⁷ m
(C) 1 × 10⁻⁶ m
(D) 2 × 10⁻⁶ m
Answer: (D)
Year: 2024 | Set: M2

Q53. In Young’s experiment, the ratio of intensities of bright and dark fringes is 9:1. The ratio of amplitude of coherent sources is
(A) 2:1
(B) 3:1
(C) √3:1
(D) 1:3
Answer: (B)
Year: 2023 | Set: Q1

Q54. The central fringe in Young’s double slit experiment is
(A) Dark
(B) Coloured
(C) Bright
(D) Absent
Answer: (C)
Year: 2022 | Set: R2

Q55. Which of the following conditions is essential for interference?
(A) Equal amplitude
(B) Same frequency
(C) Equal intensity
(D) Large separation
Answer: (B)
Year: 2022 | Set: S2

Q56. When a beam of plane polarized light is passed through a polaroid, the intensity of transmitted light is
(A) Maximum
(B) Half
(C) Zero
(D) Variable
Answer: (B)
Year: 2021 | Set: T3

Q57. Which principle explains interference and diffraction?
(A) Newton’s laws
(B) Huygens’ principle
(C) Faraday’s law
(D) Gauss’s law
Answer: (B)
Year: 2021 | Set: Q3

Q58. Brewster angle is the angle of incidence for which the reflected light is
(A) Partially polarized
(B) Unpolarized
(C) Fully polarized
(D) Doubly refracted
Answer: (C)
Year: 2020 | Set: R1

Q59. A monochromatic light of wavelength 6000 Å is used in Young’s double slit experiment. If the fringe width is 3 mm, what is the separation between the slits? (Screen distance = 1 m)
(A) 0.2 mm
(B) 0.4 mm
(C) 0.6 mm
(D) 0.8 mm
Answer: (A)
Year: 2020 | Set: S1

Q60. Light exhibits wave nature in
(A) Interference
(B) Photoelectric effect
(C) Compton effect
(D) Pair production
Answer: (A)
Year: 2019 | Set: M1

Q61. Fringe width is directly proportional to
(A) Distance between slits
(B) Distance between slits and screen
(C) Inverse of wavelength
(D) Refractive index of medium
Answer: (B)
Year: 2019 | Set: M2

Q62. In Young’s experiment, distance between slits is 0.5 mm, screen distance is 1 m and fringe width is 1 mm. The wavelength of light used is
(A) 500 nm
(B) 600 nm
(C) 650 nm
(D) 700 nm
Answer: (A)
Year: 2018 | Set: N3

Q63. Which of the following phenomena cannot be explained using Huygens’ principle?
(A) Reflection
(B) Refraction
(C) Interference
(D) Photoelectric effect
Answer: (D)
Year: 2018 | Set: Z

Q64. Which of the following proves the transverse nature of light?
(A) Interference
(B) Polarisation
(C) Diffraction
(D) Reflection
Answer: (B)
Year: 2017 | Set: T2

Q65. A polarized light is incident on another polaroid at 45° angle. The intensity of light transmitted is
(A) I
(B) I/2
(C) I/4
(D) I cos²45°
Answer: (D)
Year: 2017 | Set: P1

Q66. For sustained interference, the necessary condition is
(A) Equal wavelength
(B) Same amplitude
(C) Constant phase difference
(D) Same medium
Answer: (C)
Year: 2016 | Set: Q2

Q67. In interference, when the crest of one wave overlaps with the trough of another, the interference is
(A) Destructive
(B) Constructive
(C) Maximum
(D) Polarised
Answer: (A)
Year: 2016 | Set: M

Q68. A light wave enters from air into glass. The property that remains unchanged is
(A) Frequency
(B) Wavelength
(C) Speed
(D) Amplitude
Answer: (A)
Year: 2015 | Set: C

Q69. In Young’s double slit experiment, the intensity at a point on the screen where the path difference is λ/2 is
(A) Maximum
(B) Minimum
(C) Half of maximum
(D) One-fourth of maximum
Answer: (B)
Year: 2015 | Set: M

Q70. The minimum condition for destructive interference in thin films is
(A) Path difference = nλ
(B) Path difference = (2n + 1)λ/2
(C) Phase difference = π
(D) Amplitude = zero
Answer: (B)
Year: 2014 | Set: A

Q71. The intensity of central maximum in single slit diffraction is
(A) Equal to first maximum
(B) Half of first maximum
(C) Four times the first maximum
(D) More than double the first maximum
Answer: (D)
Year: 2014 | Set: P

Q72. Polarization can be used to distinguish between
(A) Transverse and longitudinal waves
(B) Light and sound
(C) Electric and magnetic fields
(D) High and low frequency waves
Answer: (A)
Year: 2013 | Set: R

Q73. A monochromatic beam is incident normally on a diffraction grating. If the number of lines is increased, the resolving power
(A) Increases
(B) Decreases
(C) Remains same
(D) Becomes zero
Answer: (A)
Year: 2013 | Set: N

Q74. In Young’s experiment, if the width of slits is increased
(A) Fringe visibility increases
(B) Fringe visibility decreases
(C) Fringe width increases
(D) Fringe pattern vanishes
Answer: (A)
Year: 2012 | Set: M

Q75. A polarized beam of light is incident on a polaroid. The transmitted intensity becomes zero when the axis of polaroid is
(A) Parallel to polarization
(B) Perpendicular to polarization
(C) At 45°
(D) At 60°
Answer: (B)
Year: 2012 | Set: X

Q76. Diffraction of light increases when
(A) Slit width increases
(B) Wavelength increases
(C) Distance from screen increases
(D) Intensity increases
Answer: (B)
Year: 2011 | Set: Y

Q77. The ratio of maximum and minimum intensities in an interference pattern is 9:1. What is the ratio of the amplitudes?
(A) 3:1
(B) 2:1
(C) 1:3
(D) 9:1
Answer: (A)
Year: 2011 | Set: A

Q78. Which of the following is not essential for Young’s experiment?
(A) Coherent sources
(B) Equal intensities
(C) Same frequency
(D) Same polarization
Answer: (B)
Year: 2010 | Set: Z

Q79. If in Young’s experiment, the slit separation is doubled, the fringe width becomes
(A) Double
(B) Half
(C) Four times
(D) One-fourth
Answer: (B)
Year: 2010 | Set: R

Q80. A beam of light is incident at Brewster’s angle on air-glass interface. The angle between reflected and refracted ray is
(A) 0°
(B) 45°
(C) 60°
(D) 90°
Answer: (D)
Year: 2009 | Set: S

Q81. The central fringe in Young’s double slit is
(A) Bright due to path difference zero
(B) Dark due to destructive interference
(C) Narrower than others
(D) Absent
Answer: (A)
Year: 2009 | Set: T

Q82. In Young’s experiment, when the distance between the slits is increased
(A) Fringe width increases
(B) Fringe width decreases
(C) Fringe width remains same
(D) No fringe is formed
Answer: (B)
Year: 2008 | Set: R

Q83. A light beam passes through two polaroids. The angle between the pass axes is 60°. The transmitted intensity is
(A) I
(B) I/2
(C) I/4
(D) I cos²60°
Answer: (D)
Year: 2008 | Set: Y

Q84. The light used in a single slit diffraction experiment is replaced by light of longer wavelength. The diffraction bands
(A) Become narrower
(B) Become wider
(C) Remain the same
(D) Disappear
Answer: (B)
Year: 2007 | Set: Q

Q85. In a single slit diffraction, the second minimum is observed at
(A) a sin θ = 2λ
(B) a sin θ = λ
(C) a sin θ = λ/2
(D) a sin θ = 3λ
Answer: (A)
Year: 2007 | Set: S

Q86. A plane polarized light is passed through a polaroid. The intensity of emerging light is given by
(A) I = I₀
(B) I = I₀/2
(C) I = I₀ cos²θ
(D) I = I₀ sin²θ
Answer: (C)
Year: 2006 | Set: M

Q87. Interference pattern is due to
(A) Addition of amplitudes
(B) Addition of intensities
(C) Subtraction of intensities
(D) Multiplication of amplitudes
Answer: (A)
Year: 2006 | Set: N

Q88. A source emits unpolarized light. The maximum intensity through two ideal polaroids placed at an angle θ is
(A) I₀ sin²θ
(B) I₀ cos²θ
(C) I₀/2 cos²θ
(D) I₀ cosθ
Answer: (C)
Year: 2005 | Set: Q

Q89. In Young’s experiment, to obtain more fringe separation
(A) Increase slit separation
(B) Decrease wavelength
(C) Decrease screen distance
(D) Increase screen distance
Answer: (D)
Year: 2005 | Set: R

Q90. What is the path difference corresponding to a phase difference of π in light waves of wavelength λ?
(A) λ
(B) λ/2
(C) 2λ
(D) Zero
Answer: (B)
Year: 2004 | Set: S

Q91. The separation between slits in YDSE is 0.5 mm, and screen is 1 m away. What is the fringe width for light of wavelength 600 nm?
(A) 0.12 mm
(B) 1.2 mm
(C) 0.6 mm
(D) 2.4 mm
Answer: (B)
Year: 2004 | Set: A

Q92. When a light beam is incident at Brewster’s angle on a surface, the reflected light is
(A) Circularly polarized
(B) Elliptically polarized
(C) Unpolarized
(D) Linearly polarized
Answer: (D)
Year: 2003 | Set: P

Q93. The wavefront for a beam of light from a point source is
(A) Cylindrical
(B) Planar
(C) Spherical
(D) Conical
Answer: (C)
Year: 2003 | Set: Q

Q94. The condition for destructive interference is
(A) Path difference = nλ
(B) Phase difference = 0
(C) Phase difference = π
(D) Amplitude = 0
Answer: (C)
Year: 2002 | Set: Z

Q95. In a diffraction pattern, the position of first minimum is determined by
(A) Path difference
(B) Phase difference
(C) Slit width
(D) All of these
Answer: (D)
Year: 2002 | Set: Y

Q96. The wavelength of light is doubled. The angular width of central maximum in single slit diffraction will
(A) Halve
(B) Double
(C) Remain same
(D) Become one-fourth
Answer: (B)
Year: 2001 | Set: X

Q97. If Young’s experiment is performed in water, the fringe width
(A) Increases
(B) Decreases
(C) Remains same
(D) Becomes infinite
Answer: (B)
Year: 2001 | Set: Y

Q98. In a diffraction pattern, central maximum is
(A) Brightest and widest
(B) Bright and equal to others
(C) Dimmer than others
(D) Absent
Answer: (A)
Year: 2001 | Set: A

Q99. Which of the following cannot be polarized?
(A) Light
(B) X-rays
(C) Sound waves
(D) Radio waves
Answer: (C)
Year: 2001 | Set: B

Q100. In Young’s experiment, increasing slit width affects fringe contrast by
(A) Increasing it
(B) Decreasing it
(C) No effect
(D) Eliminating fringes
Answer: (A)
Year: 2001 | Set: Z

JEE MAINS QUESTIONS FROM THIS LESSON

Q1. In Young’s double slit experiment, the distance between the slits is halved and the distance between the slits and the screen is doubled. The fringe width becomes
(A) Four times
(B) Twice
(C) Half
(D) One-fourth
Answer: (A)
Year: 2025 | Shift: 1 | Set: A

Q2. A beam of unpolarised light is incident on a glass slab at Brewster’s angle. The reflected light is
(A) Circularly polarised
(B) Plane polarised
(C) Elliptically polarised
(D) Unpolarised
Answer: (B)
Year: 2025 | Shift: 2 | Set: B

Q3. In Young’s double slit experiment, the central fringe is
(A) Always bright
(B) Always dark
(C) Can be bright or dark
(D) Coloured
Answer: (A)
Year: 2024 | Shift: 1 | Set: A

Q4. Light shows wave nature in
(A) Photoelectric effect
(B) Interference
(C) Compton effect
(D) Pair production
Answer: (B)
Year: 2024 | Shift: 2 | Set: C

Q5. The intensity of light emerging from a Polaroid is I₀. After passing through a second Polaroid rotated by 60°, the emerging intensity is
(A) I₀
(B) I₀/2
(C) I₀/4
(D) I₀ cos²60°
Answer: (D)
Year: 2023 | Shift: 2 | Set: B

Q6. In a single slit diffraction experiment, the angular width of central maximum is 60°, and the slit width is 1 μm. The wavelength of light used is
(A) 1000 nm
(B) 500 nm
(C) 750 nm
(D) 1500 nm
Answer: (A)
Year: 2023 | Shift: 1 | Set: A

Q7. Polarisation proves
(A) Transverse nature of light
(B) Longitudinal nature of light
(C) Both longitudinal and transverse
(D) None of these
Answer: (A)
Year: 2022 | Shift: 2 | Set: C

Q8. Two coherent sources of light produce interference fringes. If the separation between slits is doubled and the distance to the screen remains the same, the fringe width
(A) Doubles
(B) Halves
(C) Quadruples
(D) Remains the same
Answer: (B)
Year: 2022 | Shift: 1 | Set: A

Q9. The ratio of intensities at maxima and minima in an interference pattern is 49:9. The ratio of the amplitudes of the sources is
(A) 7:3
(B) 3:7
(C) 2:1
(D) 1:2
Answer: (A)
Year: 2021 | Shift: 1 | Set: B

Q10. Which of the following experiments confirms the transverse nature of light?
(A) Interference
(B) Diffraction
(C) Polarisation
(D) Reflection
Answer: (C)
Year: 2021 | Shift: 2 | Set: C

Q11. If two coherent light sources have amplitudes in the ratio 3:2, the intensity ratio of maxima to minima will be
(A) 25:1
(B) 5:1
(C) 9:4
(D) 6:1
Answer: (A)
Year: 2020 | Shift: 1 | Set: A

Q12. Which of the following can be used to produce interference of light?
(A) Two independent sources
(B) Two coherent sources
(C) Two diffused sources
(D) Two laser beams of different frequency
Answer: (B)
Year: 2020 | Shift: 2 | Set: B

Q13. In Young’s double slit experiment, the fringe width is β. If the whole apparatus is immersed in water, the new fringe width becomes
(A) β/μ
(B) μβ
(C) β
(D) μ²β
Answer: (A)
Year: 2019 | Shift: 1 | Set: C

Q14. Brewster’s law is used to determine
(A) Wavelength
(B) Refractive index
(C) Frequency
(D) Velocity
Answer: (B)
Year: 2019 | Shift: 2 | Set: A

Q15. Two beams of light having intensities I and 4I interfere to produce a fringe pattern. The maximum to minimum intensity ratio is
(A) 9:1
(B) 5:1
(C) 25:1
(D) 16:1
Answer: (A)
Year: 2018 | Shift: 2 | Set: D

Q16. A wavefront from a distant star reaches Earth. It is approximately
(A) Circular
(B) Planar
(C) Cylindrical
(D) Spherical
Answer: (B)
Year: 2018 | Shift: 1 | Set: B

Q17. In single slit diffraction, width of central maximum is
(A) Inversely proportional to slit width
(B) Proportional to slit width
(C) Independent of slit width
(D) Inversely proportional to square of slit width
Answer: (A)
Year: 2017 | Shift: 2 | Set: C

Q18. The reflected light from a transparent medium is completely polarised when
(A) Angle of incidence is 0°
(B) Refracted angle is 0°
(C) Reflected and refracted rays are at 90°
(D) Angle of reflection is 90°
Answer: (C)
Year: 2017 | Shift: 1 | Set: A

Q19. If light waves suffer a phase change of π, the resultant intensity will be
(A) Maximum
(B) Zero
(C) Half
(D) Quarter
Answer: (B)
Year: 2016 | Shift: 2 | Set: D

Q20. The angular position of the first diffraction minimum of a single slit depends on
(A) Intensity
(B) Wavelength and slit width
(C) Amplitude
(D) Speed of light
Answer: (B)
Year: 2016 | Shift: 1 | Set: A

Q21. When unpolarised light is incident on a polaroid, the intensity of the transmitted light is
(A) I
(B) I/2
(C) Zero
(D) 2I
Answer: (B)
Year: 2015 | Shift: 2 | Set: B

Q22. Two light waves with amplitudes 3 and 4 interfere. The maximum intensity is
(A) 49
(B) 7
(C) 25
(D) 9
Answer: (A)
Year: 2015 | Shift: 1 | Set: A

Q23. A diffraction pattern is obtained using a parallel beam of light. The slit width is decreased. The width of the central maximum will
(A) Increase
(B) Decrease
(C) Remain the same
(D) Disappear
Answer: (A)
Year: 2014 | Shift: 2 | Set: D

Q24. In YDSE, central maximum is observed when
(A) Path difference = λ
(B) Phase difference = π
(C) Path difference = 0
(D) Path difference = λ/2
Answer: (C)
Year: 2014 | Shift: 1 | Set: B

Q25. Which of the following cannot be polarised?
(A) Light
(B) X-rays
(C) Radio waves
(D) Sound waves
Answer: (D)
Year: 2013 | Shift: 2 | Set: A

Q26. In Young’s double slit experiment, the wavelength of light used is 600 nm, the screen is placed at 2 m, and the distance between slits is 1 mm. The fringe width is
(A) 0.12 mm
(B) 1.2 mm
(C) 2.0 mm
(D) 3.0 mm
Answer: (B)
Year: 2013 | Shift: 1 | Set: C

Q27. In an interference experiment, fringe width is increased if
(A) Slit separation is decreased
(B) Screen is moved closer
(C) Wavelength is decreased
(D) None of these
Answer: (A)
Year: 2012 | Shift: 2 | Set: B

Q28. Two light sources are said to be coherent if
(A) They have same wavelength
(B) They have same amplitude
(C) They have constant phase difference
(D) They are monochromatic
Answer: (C)
Year: 2012 | Shift: 1 | Set: A

Q29. Polarisation of light can be used to
(A) Determine velocity of light
(B) Distinguish between longitudinal and transverse waves
(C) Determine wavelength
(D) Determine amplitude
Answer: (B)
Year: 2011 | Shift: 2 | Set: D

Q30. For a beam of unpolarized light of intensity I₀ incident on a polarizer, the intensity of transmitted light is
(A) I₀
(B) I₀/4
(C) I₀/2
(D) 2I₀
Answer: (C)
Year: 2011 | Shift: 1 | Set: A

Q31. In single slit diffraction, the position of the first minimum is given by
(A) a sinθ = λ
(B) a cosθ = λ
(C) a tanθ = λ
(D) a sinθ = 2λ
Answer: (A)
Year: 2010 | Shift: 2 | Set: B

Q32. When white light is used in YDSE, the central fringe is
(A) Black
(B) White
(C) Colored
(D) Absent
Answer: (B)
Year: 2010 | Shift: 1 | Set: C

Q33. When the separation between the slits is increased in YDSE, the fringe width
(A) Increases
(B) Decreases
(C) Remains unchanged
(D) Becomes zero
Answer: (B)
Year: 2009 | Shift: 2 | Set: A

Q34. If a monochromatic light is used in single slit diffraction, and the slit width is decreased, the width of the central maximum
(A) Increases
(B) Decreases
(C) Remains the same
(D) Disappears
Answer: (A)
Year: 2009 | Shift: 1 | Set: B

Q35. Brewster’s angle is related to refractive index by
(A) tan i = n
(B) sin i = 1/n
(C) sin i = n
(D) tan i = 1/n
Answer: (A)
Year: 2008 | Shift: 2 | Set: C

Q36. In diffraction pattern due to single slit, the central maximum is
(A) Brightest and widest
(B) Same as other fringes
(C) Absent
(D) Dark
Answer: (A)
Year: 2008 | Shift: 1 | Set: A

Q37. In YDSE, if the wavelength of light used is doubled, the fringe width becomes
(A) Same
(B) Half
(C) Double
(D) Four times
Answer: (C)
Year: 2007 | Shift: 2 | Set: D

Q38. In interference, the intensity is maximum when the phase difference is
(A) π
(B) 0
(C) π/2
(D) 3π/2
Answer: (B)
Year: 2007 | Shift: 1 | Set: B

Q39. Diffraction is not observed with sound waves because
(A) Wavelength is large
(B) Wavelength is small
(C) Velocity is high
(D) None of these
Answer: (A)
Year: 2006 | Shift: 2 | Set: C

Q40. Interference occurs due to
(A) Addition of amplitudes
(B) Addition of intensities
(C) Subtraction of frequencies
(D) Polarisation
Answer: (A)
Year: 2006 | Shift: 1 | Set: A

Q41. When light passes through two crossed polaroids, the transmitted intensity is
(A) Maximum
(B) Minimum
(C) Half
(D) Quarter
Answer: (B)
Year: 2005 | Shift: 2 | Set: D

Q42. In Young’s double slit experiment, the maximum fringe width is observed for
(A) Red light
(B) Blue light
(C) Green light
(D) Violet light
Answer: (A)
Year: 2005 | Shift: 1 | Set: B

Q43. The transverse nature of light is proved by
(A) Reflection
(B) Refraction
(C) Diffraction
(D) Polarisation
Answer: (D)
Year: 2004 | Shift: 2 | Set: C

Q44. Two light waves superpose with phase difference π/2. The resultant intensity is
(A) Maximum
(B) Zero
(C) Half of max
(D) Three-fourths of max
Answer: (D)
Year: 2004 | Shift: 1 | Set: A

Q45. In single slit diffraction, angular width of central maximum is
(A) 2λ/a
(B) λ/a
(C) a/λ
(D) 2a/λ
Answer: (A)
Year: 2003 | Shift: 2 | Set: B

Q46. In YDSE, path difference of λ produces
(A) Constructive interference
(B) Destructive interference
(C) Zero intensity
(D) Maximum amplitude
Answer: (A)
Year: 2003 | Shift: 1 | Set: A

Q47. The polarisation of light proves
(A) Light is longitudinal
(B) Light is transverse
(C) Light is scalar
(D) Light is electromagnetic
Answer: (B)
Year: 2002 | Shift: 2 | Set: D

Q48. The ratio of intensity at maximum and minimum in interference is 36:4. The amplitude ratio is
(A) 3:1
(B) 2:1
(C) 6:1
(D) 9:1
Answer: (C)
Year: 2002 | Shift: 1 | Set: C

Q49. Two coherent sources produce fringe width β. If wavelength is doubled, new fringe width is
(A) 2β
(B) β/2
(C) β
(D) 4β
Answer: (A)
Year: 2001 | Shift: 2 | Set: A

Q50. A beam of light of intensity I is incident on a polaroid. The intensity of light transmitted through analyzer at 30° is
(A) I
(B) I/2
(C) I cos²30°
(D) Zero
Answer: (C)
Year: 2001 | Shift: 1 | Set: B

————————————————————————————————————————————————————————————————————————————

JEE ADVANCED QUESTIONS FROM THIS LESSON

📘 JEE Advanced – Paper 1 – Wave Optics (Q1–Q17)
Q1. In Young’s double slit experiment, the wavelength of light is 500 nm. If the fringe width is 5 mm and the distance between slits is 1 mm, the distance between slits and screen is
(A) 1 m
(B) 2 m
(C) 0.5 m
(D) 0.1 m
Answer: (A)
Year: 2025 | Paper: 1 | Set: 1

Q2. A beam of unpolarised light of intensity I is incident on a polaroid. The intensity of light transmitted through it is
(A) I
(B) I/2
(C) 2I
(D) 0
Answer: (B)
Year: 2024 | Paper: 1 | Set: 2

Q3. A ray of light is incident at Brewster’s angle on the interface of a transparent medium and air. The reflected ray is
(A) Partially polarized
(B) Unpolarized
(C) Completely polarized
(D) Doubly refracted
Answer: (C)
Year: 2023 | Paper: 1 | Set: 1

Q4. The interference pattern in Young’s experiment shifts when
(A) Screen is moved
(B) One slit is closed
(C) Light source is replaced
(D) Medium between slits and screen changes
Answer: (D)
Year: 2022 | Paper: 1 | Set: 2

Q5. The angular width of central maximum in single slit diffraction is inversely proportional to
(A) Wavelength
(B) Slit width
(C) Square of wavelength
(D) Square of slit width
Answer: (B)
Year: 2021 | Paper: 1 | Set: 1

Q6. In YDSE, the path difference for constructive interference is
(A) (2n + 1)λ/2
(B) nλ
(C) nλ/2
(D) Zero
Answer: (B)
Year: 2020 | Paper: 1 | Set: 2

Q7. The central fringe in white light interference is
(A) Bright and white
(B) Dark
(C) Coloured
(D) Absent
Answer: (A)
Year: 2019 | Paper: 1 | Set: 1

Q8. The transverse nature of light is confirmed by
(A) Reflection
(B) Refraction
(C) Polarisation
(D) Diffraction
Answer: (C)
Year: 2018 | Paper: 1 | Set: 2

Q9. The fringe width in Young’s experiment is 0.2 cm. If whole setup is immersed in water (μ = 4/3), the fringe width becomes
(A) 0.15 cm
(B) 0.20 cm
(C) 0.30 cm
(D) 0.133 cm
Answer: (D)
Year: 2017 | Paper: 1 | Set: 1

Q10. When two coherent sources interfere, the resultant intensity is maximum when the phase difference is
(A) π
(B) 0
(C) π/2
(D) 3π
Answer: (B)
Year: 2016 | Paper: 1 | Set: 2

Q11. If one slit in YDSE is closed, the pattern on screen is due to
(A) No light
(B) Interference
(C) Diffraction
(D) Reflection
Answer: (C)
Year: 2015 | Paper: 1 | Set: 1

Q12. The resolving power of a diffraction grating increases with
(A) Wavelength
(B) Number of lines
(C) Slit width
(D) Amplitude
Answer: (B)
Year: 2014 | Paper: 1 | Set: 2

Q13. A wavefront from a distant star reaching Earth is
(A) Spherical
(B) Planar
(C) Cylindrical
(D) Conical
Answer: (B)
Year: 2013 | Paper: 1 | Set: 1

Q14. If fringe width is β, the distance between two bright fringes is
(A) 2β
(B) β
(C) β/2
(D) 4β
Answer: (B)
Year: 2012 | Paper: 1 | Set: 2

Q15. When the angle between the transmission axes of two polaroids is 60°, the transmitted intensity is
(A) I
(B) I/2
(C) I/4
(D) I cos²60°
Answer: (D)
Year: 2011 | Paper: 1 | Set: 1

Q16. Diffraction increases with
(A) Slit width
(B) Wavelength
(C) Screen distance
(D) Intensity
Answer: (B)
Year: 2010 | Paper: 1 | Set: 2

Q17. Brewster’s law relates the angle of incidence and
(A) Refractive index
(B) Frequency
(C) Amplitude
(D) Speed
Answer: (A)
Year: 2009 | Paper: 1 | Set: 1

📗 JEE Advanced – Paper 2 – Wave Optics (Q18–Q34)
Q18. A light wave is incident at 45° on a glass surface (μ = 1.5). The reflected light is completely polarized when
(A) i = 45°
(B) i = tan⁻¹(μ)
(C) r = 45°
(D) r = 90°
Answer: (B)
Year: 2025 | Paper: 2 | Set: 1

Q19. The ratio of intensities at maxima and minima in an interference pattern is 25:1. The ratio of amplitudes is
(A) 5:1
(B) 3:1
(C) 2:1
(D) 6:1
Answer: (A)
Year: 2024 | Paper: 2 | Set: 2

Q20. In single slit diffraction, the first minimum occurs at
(A) a sinθ = λ
(B) a cosθ = λ
(C) a tanθ = λ
(D) a sinθ = 2λ
Answer: (A)
Year: 2023 | Paper: 2 | Set: 1

Q21. A polaroid transmits light of intensity I. After passing through another polaroid at 30°, intensity becomes
(A) I
(B) I/2
(C) I cos²30°
(D) I sin²30°
Answer: (C)
Year: 2022 | Paper: 2 | Set: 2

Q22. When light of wavelength 600 nm passes through a single slit of width 2 μm, the angular width of central maximum is
(A) 0.3 rad
(B) 0.6 rad
(C) 0.15 rad
(D) 0.05 rad
Answer: (B)
Year: 2021 | Paper: 2 | Set: 1

Q23. In YDSE, distance between slits = 0.5 mm, screen distance = 2 m, and fringe width = 2.4 mm. The wavelength of light is
(A) 600 nm
(B) 500 nm
(C) 480 nm
(D) 400 nm
Answer: (A)
Year: 2020 | Paper: 2 | Set: 2

Q24. Polarisation is not shown by
(A) Light
(B) Sound
(C) X-rays
(D) Microwaves
Answer: (B)
Year: 2019 | Paper: 2 | Set: 1

Q25. When light is incident at Brewster’s angle, the reflected and refracted rays are
(A) Parallel
(B) Perpendicular
(C) Same
(D) 45° apart
Answer: (B)
Year: 2018 | Paper: 2 | Set: 2

Q26. For destructive interference in YDSE, path difference must be
(A) λ
(B) nλ
(C) (2n+1)λ/2
(D) Zero
Answer: (C)
Year: 2017 | Paper: 2 | Set: 1

Q27. Which phenomenon is not explained by Huygens’ principle?
(A) Diffraction
(B) Reflection
(C) Photoelectric effect
(D) Refraction
Answer: (C)
Year: 2016 | Paper: 2 | Set: 2

Q28. The shape of wavefront due to a point source is
(A) Plane
(B) Cylindrical
(C) Spherical
(D) Elliptical
Answer: (C)
Year: 2015 | Paper: 2 | Set: 1

Q29. The fringe visibility improves if
(A) Intensities are equal
(B) Wavelength is increased
(C) Slits are wider
(D) Slits are far apart
Answer: (A)
Year: 2014 | Paper: 2 | Set: 2

Q30. The polarising angle of a medium with refractive index 1.73 is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
Answer: (C)
Year: 2013 | Paper: 2 | Set: 1

Q31. The minimum condition for constructive interference is
(A) Path difference = λ
(B) Phase difference = π
(C) Path difference = nλ
(D) Amplitude = 0
Answer: (C)
Year: 2012 | Paper: 2 | Set: 2

Q32. When light passes through two crossed polaroids, the intensity is
(A) I
(B) I/2
(C) 0
(D) I/4
Answer: (C)
Year: 2011 | Paper: 2 | Set: 1

Q33. In YDSE, when one slit is covered with thin glass, the central fringe
(A) Shifts
(B) Disappears
(C) Remains same
(D) Is dark
Answer: (A)
Year: 2010 | Paper: 2 | Set: 2

Q34. The intensity in YDSE at path difference λ/2 is
(A) I₀
(B) 0
(C) Maximum
(D) Half
Answer: (B)
Year: 2009 | Paper: 2 | Set: 1

PRACTICE SETS FROM THIS LESSON

Q1. Which phenomenon best proves the wave nature of light?
(A) Reflection
(B) Refraction
(C) Interference
(D) Dispersion
Answer: (C)

Q2. The central maximum in a single slit diffraction is
(A) Narrow and dark
(B) Broad and bright
(C) Narrow and bright
(D) Broad and dark
Answer: (B)

Q3. In Young’s double slit experiment, if the slit separation is doubled, the fringe width becomes
(A) Doubled
(B) Halved
(C) Four times
(D) One-fourth
Answer: (B)

Q4. The ratio of intensities at maxima and minima in an interference pattern is 49:9. The amplitude ratio of the sources is
(A) 2:1
(B) 3:2
(C) 7:3
(D) 5:1
Answer: (C)

Q5. When unpolarised light is incident on a polaroid, the transmitted intensity is
(A) 0
(B) I
(C) I/2
(D) 2I
Answer: (C)

Q6. A light of wavelength 600 nm falls on a single slit of width 2 µm. The angular width of the central maximum is approximately
(A) 0.6 rad
(B) 0.3 rad
(C) 0.1 rad
(D) 1.2 rad
Answer: (A)

Q7. Two coherent sources produce interference. If their amplitudes are equal, the visibility of fringes is
(A) 1
(B) 0.5
(C) 0
(D) 2
Answer: (A)

Q8. Brewster’s angle for a medium with refractive index √3 is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
Answer: (C)

Q9. The angular position of the first minimum in single slit diffraction is given by
(A) sinθ = λ/a
(B) cosθ = λ/a
(C) tanθ = λ/a
(D) sinθ = 2λ/a
Answer: (A)

Q10. In Young’s experiment, if the screen is moved farther from the slits, the fringe width
(A) Increases
(B) Decreases
(C) Remains constant
(D) Becomes zero
Answer: (A)

Q11. Polarisation occurs only in
(A) Longitudinal waves
(B) Transverse waves
(C) Both
(D) Neither
Answer: (B)

Q12. The condition for destructive interference is
(A) Phase difference = 0
(B) Path difference = nλ
(C) Phase difference = π
(D) Wavelengths must differ
Answer: (C)

Q13. Which of the following changes fringe width in YDSE?
(A) Intensity
(B) Slit width
(C) Screen distance
(D) Coherence
Answer: (C)

Q14. The unit of fringe width is
(A) m⁻¹
(B) rad
(C) m
(D) Hz
Answer: (C)

Q15. Which of the following can be polarised?
(A) Sound
(B) Heat
(C) Light
(D) Pressure
Answer: (C)

Q16. The central fringe in YDSE with white light is
(A) Red
(B) Blue
(C) White
(D) Black
Answer: (C)

Q17. Interference is not observed with two ordinary bulbs because
(A) They are dim
(B) Their frequencies differ
(C) They are incoherent
(D) They are coherent
Answer: (C)

Q18. The mathematical expression for fringe width is
(A) λd/D
(B) Dλ/d
(C) dλ/D
(D) λD/d
Answer: (D)

Q19. Huygens’ principle can explain
(A) Photoelectric effect
(B) Reflection
(C) Compton scattering
(D) Polarisation
Answer: (B)

Q20. The maximum number of fringes possible in YDSE depends on
(A) Wavelength only
(B) Slit separation
(C) Width of slits
(D) Width of coherent source
Answer: (B)

Q21. Which of the following will increase fringe visibility in interference?
(A) Unequal amplitude
(B) Monochromatic light
(C) Different frequencies
(D) Incoherent sources
Answer: (B)

Q22. If the separation between two slits is halved and screen distance is doubled, the fringe width
(A) Increases 4 times
(B) Remains unchanged
(C) Increases 2 times
(D) Doubles
Answer: (A)

Q23. When a beam of unpolarised light passes through two polaroids at 90°, the output is
(A) I
(B) I/2
(C) 0
(D) I/4
Answer: (C)

Q24. A source emits light at wavelength λ. It produces interference fringes of width β. If wavelength becomes 2λ, the new fringe width is
(A) β/2
(B) 2β
(C) 4β
(D) β
Answer: (B)

Q25. Wavefronts emerging from a convex lens are
(A) Cylindrical
(B) Diverging
(C) Planar
(D) Converging spherical
Answer: (D)

Q26. If in single slit diffraction, width of slit is doubled, the angular width of central maximum
(A) Doubles
(B) Becomes half
(C) Remains same
(D) Becomes zero
Answer: (B)

Q27. In polarisation, Malus law states
(A) I ∝ cos²θ
(B) I ∝ sinθ
(C) I ∝ tan²θ
(D) I ∝ θ
Answer: (A)

Q28. If two waves of intensity I and 3I interfere, the resultant maximum intensity is
(A) 2I
(B) 4I
(C) 6.9I
(D) 7.46I
Answer: (D)

Q29. Fringe width increases with
(A) Higher slit separation
(B) Shorter wavelength
(C) Longer screen distance
(D) More intensity
Answer: (C)

Q30. Central maximum in diffraction is due to
(A) Constructive interference
(B) Destructive interference
(C) Polarisation
(D) Refraction
Answer: (A)

Q31. Light is said to be plane polarised when
(A) Electric field vector rotates
(B) Magnetic field oscillates randomly
(C) Electric field oscillates in one plane
(D) Frequency remains same
Answer: (C)

Q32. Which colour gives widest fringe width in YDSE?
(A) Red
(B) Violet
(C) Blue
(D) Green
Answer: (A)

Q33. The angular width of the central maximum in single slit diffraction depends on
(A) Intensity of source
(B) Slit width and wavelength
(C) Amplitude
(D) Source size
Answer: (B)

Q34. In YDSE, when a glass plate is inserted in front of one slit, the fringe pattern
(A) Remains same
(B) Becomes coloured
(C) Shifts
(D) Disappears
Answer: (C)

Q35. In a YDSE setup, slits are 0.5 mm apart and the screen is 1.5 m away. If the wavelength of light is 600 nm, what is the fringe width?
(A) 1.8 mm
(B) 2.4 mm
(C) 1.2 mm
(D) 3.0 mm
Answer: (B)

Q36. Two coherent sources produce interference fringes. If the intensity at maxima is 36 units and at minima is 4 units, what is the ratio of amplitudes?
(A) 2:1
(B) 3:1
(C) 5:1
(D) 6:1
Answer: (D)

Q37. A monochromatic light is incident on a single slit of width 0.4 mm. The diffraction pattern is observed at a distance of 1.5 m. If the first minimum is at 2 mm from central maximum, what is the wavelength?
(A) 533 nm
(B) 600 nm
(C) 750 nm
(D) 500 nm
Answer: (C)

Q38. Light of two different wavelengths λ₁ = 600 nm and λ₂ = 400 nm are used in a YDSE setup. The fringe width for λ₁ is β₁. What is the ratio β₁:β₂?
(A) 2:1
(B) 1:2
(C) 3:2
(D) 4:3
Answer: (A)

Q39. In a diffraction experiment, if the slit width is reduced to half, the width of central maximum becomes
(A) Four times
(B) Half
(C) Double
(D) Same
Answer: (C)

Q40. The minimum number of fringes visible in Young’s experiment depends on
(A) Source frequency
(B) Screen distance
(C) Wavelength
(D) Coherence length
Answer: (D)

Q41. Two polaroids are placed at 60° angle. If unpolarized light of intensity I₀ is incident, the transmitted intensity is
(A) I₀
(B) I₀/2
(C) I₀/4
(D) 3I₀/8
Answer: (D)

Q42. A glass plate of thickness t and refractive index µ is placed in the path of one slit of a YDSE. The central fringe shifts by n fringes. Then
(A) t = nλ/µ
(B) t = nλ/(µ–1)
(C) t = nλµ
(D) t = nλ(µ–1)
Answer: (D)

Q43. Two coherent waves have amplitudes A and 2A. The intensity of the resultant wave at the point of destructive interference is
(A) A²
(B) A² + 4A²
(C) A²
(D) A²
Answer: (C)

Q44. In a diffraction experiment, the angular position θ of the first minimum is given by
(A) sinθ = λ/d
(B) sinθ = λ/a
(C) sinθ = a/λ
(D) sinθ = λ/2a
Answer: (B)

Q45. If light of intensity I passes through a polaroid and then an analyser at 30°, the final intensity is
(A) I
(B) I/2
(C) I/4
(D) 0.75I
Answer: (D)

Q46. A wavefront from a point source is
(A) Elliptical
(B) Cylindrical
(C) Plane
(D) Spherical
Answer: (D)

Q47. In Young’s experiment, the slit separation is 0.4 mm and screen is 1.2 m away. What should be the wavelength to obtain 3 mm fringe width?
(A) 1000 nm
(B) 400 nm
(C) 600 nm
(D) 720 nm
Answer: (C)

Q48. Two slits separated by 0.2 mm are illuminated by light of wavelength 500 nm. Find the fringe width if the screen is 2 m away.
(A) 2.5 mm
(B) 5 mm
(C) 1 mm
(D) 0.5 mm
Answer: (A)

Q49. A monochromatic light of wavelength 700 nm produces a diffraction pattern. If the slit width is 0.14 mm, find the angular width of central maximum.
(A) 0.01 rad
(B) 0.02 rad
(C) 0.01°
(D) 0.02°
Answer: (B)

Q50. The contrast of fringes is best when
(A) Sources have equal intensity
(B) One source is much brighter
(C) Both are incoherent
(D) One source has longer wavelength
Answer: (A)

Q51. The condition for first minimum in single slit diffraction is
(A) a sinθ = λ
(B) a sinθ = λ/2
(C) a cosθ = λ
(D) a tanθ = λ
Answer: (A)

Q52. Brewster’s angle is 56°. The refractive index of medium is
(A) 1.5
(B) 1.6
(C) 1.7
(D) 1.4
Answer: (A)

Q53. The central maximum width in diffraction pattern is 4 mm. If slit width is halved, new width will be
(A) 2 mm
(B) 4 mm
(C) 8 mm
(D) 16 mm
Answer: (C)

Q54. Which factor does not affect fringe width?
(A) Wavelength
(B) Slit separation
(C) Slit width
(D) Screen distance
Answer: (C)

Q55. Two waves having equal amplitude and a phase difference of π/2 interfere. The resultant intensity is
(A) I
(B) Zero
(C) I/2
(D) 2I
Answer: (C)

Q56. What is the angle of incidence at which light must strike a glass surface (µ = 1.5) for the reflected light to be completely polarised?
(A) 30°
(B) 45°
(C) 56.3°
(D) 60°
Answer: (C)

Q57. A 1 mm thick glass sheet (µ = 1.5) causes a fringe shift of 2 fringes in YDSE. The wavelength of light used is
(A) 300 nm
(B) 400 nm
(C) 500 nm
(D) 600 nm
Answer: (C)

Q58. When two polaroids are perpendicular to each other, the intensity of light through both is
(A) I
(B) I/2
(C) 0
(D) I/4
Answer: (C)

Q59. A polaroid reduces intensity by 50%. How much intensity is left if three identical polaroids are used in sequence?
(A) I/2
(B) I/4
(C) I/8
(D) I/6
Answer: (C)

Q60. Two light waves of amplitudes A and A interfere. The resultant amplitude is
(A) 2A
(B) A
(C) Zero
(D) A√2
Answer: (A)

Q61. If the fringe width is 2 mm and wavelength is doubled, fringe width becomes
(A) 1 mm
(B) 4 mm
(C) 3 mm
(D) 2 mm
Answer: (B)

Q62. A diffraction pattern has dark fringes at angles where
(A) a sinθ = nλ
(B) a sinθ = (2n+1)λ/2
(C) a sinθ = nλ, n ≠ 0
(D) a cosθ = nλ
Answer: (C)

Q63. A phase difference of π leads to
(A) Maximum intensity
(B) Constructive interference
(C) Destructive interference
(D) No effect
Answer: (C)

Q64. A 2 mm thick mica sheet (µ = 1.6) is inserted in one slit. The shift in central fringe is observed to be 3 mm. What is the wavelength?
(A) 600 nm
(B) 400 nm
(C) 500 nm
(D) 700 nm
Answer: (C)

Q65. If slit width in a diffraction experiment is doubled, then angular width of central maximum
(A) Doubles
(B) Becomes half
(C) Same
(D) Becomes zero
Answer: (B)

Q66. Two waves having path difference λ/4 interfere. The resultant intensity is
(A) I
(B) I/2
(C) Between 0 and I
(D) Zero
Answer: (C)

Q67. In YDSE, if the wavelength of light is increased, the number of visible fringes
(A) Increases
(B) Decreases
(C) Remains constant
(D) Doubles
Answer: (B)

Q68. A plane wave of wavelength λ passes through a single slit of width a. The angular width of the central maximum is 30°. What is the value of a/λ?
(A) 2
(B) 1
(C) 4
(D) 0.5
Answer: (A)

Q69. In a Young’s double slit experiment, a thin glass plate (μ = 1.6) of thickness 5 μm is placed in front of one slit. The wavelength of light used is 500 nm. What is the fringe shift observed?
(A) 4 fringes
(B) 6 fringes
(C) 8 fringes
(D) 10 fringes
Answer: (C)

Q70. Two slits in a YDSE are illuminated with coherent light of wavelength 600 nm. A point on the screen is 3 mm from the central maximum and 1 m away from the slits. If the slit separation is 1 mm, what is the phase difference at that point?
(A) π
(B) 2π
(C) 3π
(D) 4π
Answer: (B)

Q71. If the width of central maximum in single slit diffraction is 8 mm on a screen 1.6 m away, and the wavelength used is 640 nm, calculate the slit width.
(A) 0.025 mm
(B) 0.032 mm
(C) 0.04 mm
(D) 0.064 mm
Answer: (B)

Q72. In a polaroid experiment, the transmitted intensity is I₀/4 when two polaroids are used. What is the angle between their transmission axes?
(A) 30°
(B) 45°
(C) 60°
(D) 90°
Answer: (B)

Q73. A parallel beam of light is incident on a slit of width 2λ. What is the angular separation between first-order minima?
(A) 60°
(B) 30°
(C) 45°
(D) 90°
Answer: (D)

Q74. Two coherent light sources produce an interference pattern. If the path difference at a point is 1.5λ, what type of fringe is formed there?
(A) Central maximum
(B) Secondary maximum
(C) Secondary minimum
(D) Dark fringe
Answer: (C)

Q75. In YDSE, if the light is replaced with electrons of same wavelength (de Broglie), the fringe pattern
(A) Disappears
(B) Shifts
(C) Remains same
(D) Is magnified
Answer: (C)

Q76. In single slit diffraction, if the width of the slit becomes less than the wavelength used, the diffraction pattern
(A) Becomes sharper
(B) Vanishes
(C) Spreads widely
(D) Is inverted
Answer: (C)

Q77. Light of wavelength 600 nm passes through a slit of width 0.2 mm. Find the distance of the first minimum from the central maximum on a screen 2 m away.
(A) 3 mm
(B) 6 mm
(C) 9 mm
(D) 12 mm
Answer: (B)

Q78. For destructive interference to occur at a point on screen in YDSE, the path difference must be
(A) nλ
(B) nλ/2
(C) (2n + 1)λ/2
(D) 0
Answer: (C)

Q79. The visibility (V) of fringes in an interference pattern is defined as V = (Imax – Imin)/(Imax + Imin). For intensities I₁ = 9 and I₂ = 1, what is V?
(A) 0.8
(B) 0.6
(C) 0.9
(D) 0.5
Answer: (A)

Q80. A light of intensity I passes through a polaroid at angle θ to the axis of polarization. At what angle will the intensity reduce to I/8?
(A) 60°
(B) 45°
(C) 75.5°
(D) 30°
Answer: (C)

Q81. If a glass plate of thickness t introduces a phase shift of 2π between the two waves in YDSE, the central maximum
(A) Remains at the center
(B) Shifts by one fringe
(C) Disappears
(D) Shifts by two fringes
Answer: (A)

Q82. A circular aperture behaves like a single slit of diameter d in diffraction. The angle of the first minimum in the Airy pattern is approximately
(A) 1.22 λ/d
(B) λ/d
(C) λ/2d
(D) 2λ/d
Answer: (A)

Q83. Two polaroids are placed such that the angle between their axes is θ. The intensity of light emerging is I₀/3. Find θ.
(A) 30°
(B) 45°
(C) 60°
(D) 70.5°
Answer: (D)

Q84. In YDSE, if the entire apparatus is dipped in water (μ = 1.33), the fringe width becomes
(A) 1.33 times
(B) 0.75 times
(C) 0.5 times
(D) 1.5 times
Answer: (B)

Q85. Light of wavelength 550 nm is used in a YDSE setup with d = 0.2 mm and D = 1.5 m. The distance between 5th bright and 2nd bright fringe is
(A) 6.2 mm
(B) 4.95 mm
(C) 3.3 mm
(D) 2.75 mm
Answer: (B)

Q86. If the polaroid and analyser are placed at 0° and 60°, what percentage of incident unpolarised light intensity is transmitted?
(A) 75%
(B) 37.5%
(C) 50%
(D) 25%
Answer: (B)

Q87. In single slit diffraction, increasing the wavelength of light results in
(A) Narrower central maximum
(B) Wider central maximum
(C) Unchanged pattern
(D) More fringes
Answer: (B)

Q88. A plane wavefront is incident on a slit of width a. The diffraction pattern is observed at screen distance D. The condition for first minimum is
(A) a = λD
(B) sinθ = λ/a
(C) a = λ/2
(D) sinθ = a/λ
Answer: (B)

Q89. The phase difference between two waves producing destructive interference is
(A) 0
(B) π
(C) 2π
(D) 3π
Answer: (B)

Q90. A beam of unpolarized light of intensity I passes through a polaroid and then an analyser at 60°. Final intensity is
(A) I/2
(B) I/4
(C) 3I/8
(D) I/8
Answer: (C)

Q91. For light of λ = 500 nm and single slit of a = 0.25 mm, find angle for first diffraction minimum.
(A) 0.11 rad
(B) 0.02 rad
(C) 0.01 rad
(D) 0.001 rad
Answer: (B)

Q92. When the distance between slits in YDSE is doubled, fringe width becomes
(A) 2 times
(B) 4 times
(C) 1/2
(D) 1/4
Answer: (C)

Q93. Which experiment proves that light has transverse wave nature?
(A) Young’s experiment
(B) Polarisation
(C) Diffraction
(D) Photoelectric effect
Answer: (B)

Q94. In Young’s experiment, if one slit is covered with a mica sheet introducing optical path difference λ/2, the central fringe
(A) Remains
(B) Becomes dark
(C) Becomes bright
(D) Shifts left
Answer: (B)

Q95. Interference fringes disappear if
(A) Coherence is lost
(B) Wavelength is doubled
(C) Slit width is increased
(D) Screen is moved closer
Answer: (A)

Q96. In a single slit diffraction experiment, decreasing screen distance results in
(A) Sharper fringes
(B) Closer fringes
(C) Broader fringes
(D) Smaller angular spread
Answer: (B)

Q97. A polaroid transmits 80% of incident intensity. After passing through two such polaroids at 45° to each other, final intensity is
(A) 32%
(B) 40%
(C) 64%
(D) 50%
Answer: (A)

Q98. For interference to be sustained, the condition is
(A) Same amplitude
(B) Constant phase difference
(C) Same polarization
(D) Monochromatic light only
Answer: (B)

Q99. The relation between fringe shift x and thickness t of glass plate (μ > 1) inserted in one slit is
(A) x = tλ/μ
(B) x = (μ–1)t/λ × β
(C) x = λt/(μ–1)
(D) x = βλt/μ
Answer: (B)

Q100. Two waves interfere and produce zero intensity at a point. Their amplitudes are A and B. The phase difference is
(A) π, and A = B
(B) π, and A ≠ B
(C) Zero
(D) Cannot determine
Answer: (A)

Important Notice : The lessons and study materials up to July–August 2025 have been sent. Soon, after receiving feedback from teachers and students, we will deliver the latest and more innovative study materials for the upcoming months.

Important Notice : The lessons and study materials up to July–August 2025 have been sent. Soon, after receiving feedback from teachers and students, we will deliver the latest and more innovative study materials for the upcoming months.

Class 12 : Physics (English) – Chapter 10: Wave Optics

EXPLANATION & SUMMARY

QUESTIONS FROM TEXTBOOK

OTHER IMPORTANT QUESTIONS FOR EXAMS

NEET QUESTIONS FROM THIS LESSON

JEE MAINS QUESTIONS FROM THIS LESSON

JEE ADVANCED QUESTIONS FROM THIS LESSON

PRACTICE SETS FROM THIS LESSON

MISCONCEPTIONS “ALERTS”

KNOWLEDGE WITH FUN

MNEMONICS

Leave a Reply Cancel reply