Class 12 : Physics (English) – Chapter 7: Alternating Current
EXPLANATION & SUMMARY
🔹 1. Introduction to Alternating Current
Electric current in circuits may be direct current (DC) or alternating current (AC).
DC flows steadily in one direction (cells, batteries).
AC changes its magnitude and direction with time in a periodic fashion.
General equations:
➡️ i(t) = I0 sin(ωt) or i(t) = I0 cos(ωt)
➡️ v(t) = V0 sin(ωt) or v(t) = V0 cos(ωt)
Here:
I0, V0 = peak current and voltage
ω = angular frequency = 2πf
f = frequency of AC (India → 50 Hz, USA → 60 Hz)
T = time period = 1/f
💡 Advantage: AC is used in power supply because its voltage can be stepped up or down by transformers, enabling long-distance transmission with minimal loss.
🔹 2. RMS and Average Values
Since AC varies with time, we use effective measures:
✔️ Peak value: I0, V0 (maximum).
✔️ Root Mean Square (RMS): Equivalent DC value producing the same heating effect.
Derivation:
i(t) = I0 sin(ωt)
RMS = sqrt[(1/T) ∫0^T i² dt]
= sqrt[(I0²/2)]
➡️ Irms = I0/√2, Vrms = V0/√2
✔️ In India: Vrms = 220 V → V0 ≈ 311 V.
💡 Average value of half cycle = (2/π) I0, useful in rectifiers.
🔹 3. Pure Resistor in AC
For resistor: V = V0 sin(ωt)
I = V/R = (V0/R) sin(ωt) = I0 sin(ωt)
✔️ Current is in phase with voltage.
✔️ Power = V × I = V0 I0 sin²(ωt).
Average power = V_rms × I_rms.
💡 Application: Electric heaters, irons, geysers.
🔹 4. Pure Inductor in AC

Applied voltage: V = V0 sin(ωt)
But V = L di/dt
Solution: i(t) = (V0/ωL) sin(ωt – π/2)
✔️ Current lags voltage by 90°.
✔️ Inductive reactance: XL = ωL
💡 Example: Motors, coils, inductive chokes.
🔹 5. Pure Capacitor in AC
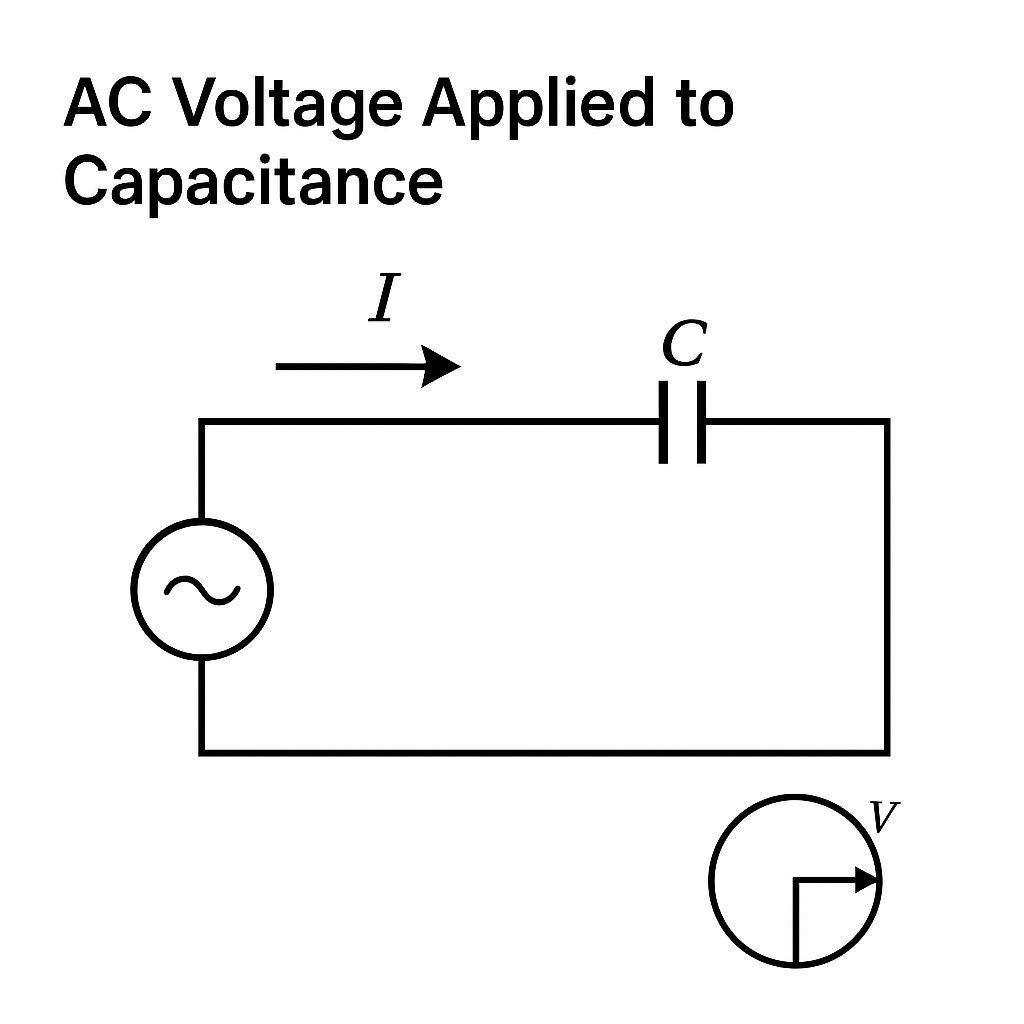
Applied voltage: V = V0 sin(ωt)
Charge q = CV → i = dq/dt = V0 ωC sin(ωt + π/2)
✔️ Current leads voltage by 90°.
✔️ Capacitive reactance: XC = 1/(ωC).
💡 Example: Ceiling fans, AC regulators.
🔹 6. Series RLC Circuit
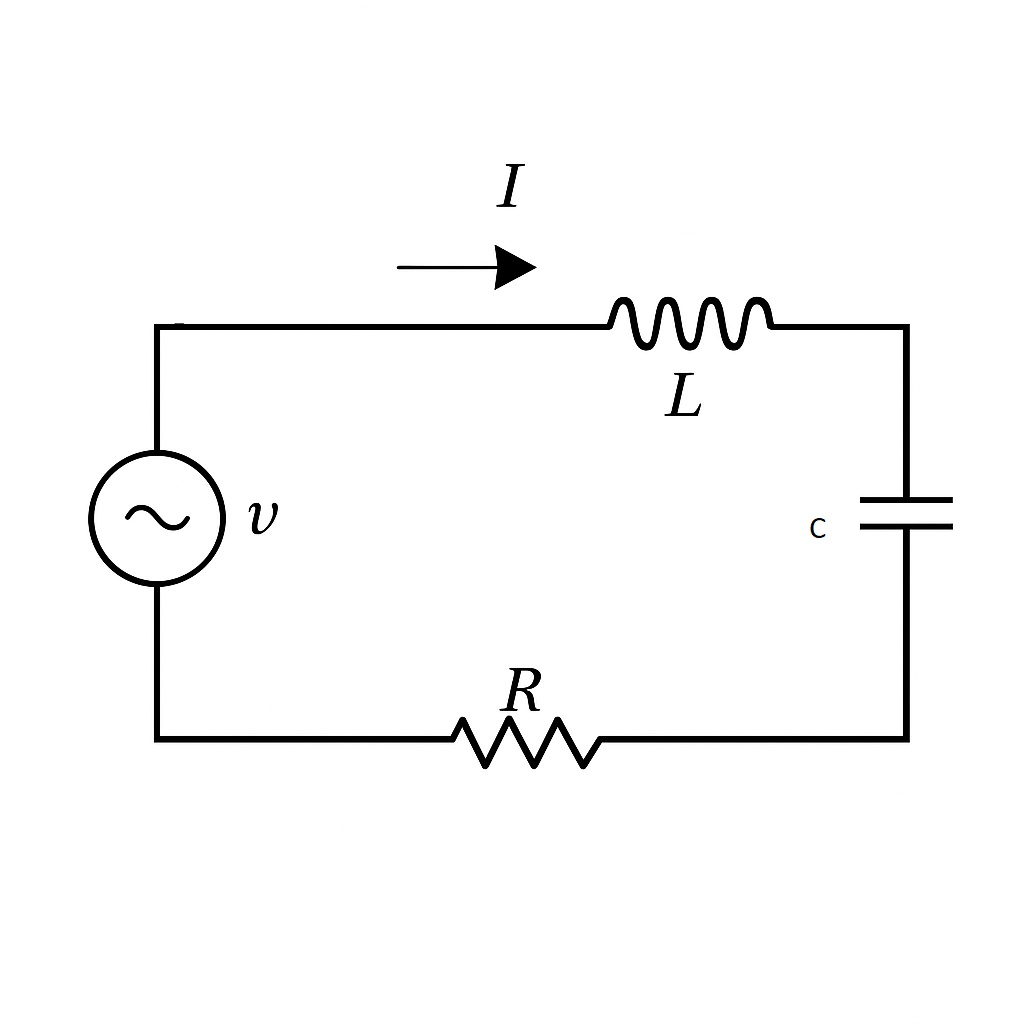
Combination of R, L, C in series with AC supply.
Impedance:
➡️ Z = sqrt(R² + (XL – XC)²)
Current:
➡️ I0 = V0/Z
Phase angle:
➡️ tanφ = (XL – XC)/R
✔️ If XL > XC → circuit inductive → current lags.
✔️ If XC > XL → circuit capacitive → current leads.
🔹 7. Resonance
Condition: XL = XC → ωL = 1/(ωC)
Resonant frequency:
➡️ fr = 1/(2π sqrt(LC))
✔️ At resonance: Z = R, I = V/R (maximum).
✔️ Voltage and current are in phase.
💡 Applications: Radio/TV tuning, oscillatory circuits.
🔹 8. Power in AC
Instantaneous power: p = v × i = V0 I0 sin²(ωt – φ).
Average power:
➡️ Pavg = Vrms Irms cosφ
Where cosφ = power factor.
✔️ Power factor close to 1 = efficient circuit.
✔️ For pure L or C → φ = ±90°, cosφ = 0 → no average power consumed.
💡 Industries correct low power factor using capacitors.
🔹 9. LC Oscillations
Charge capacitor → connect across inductor.
Energy initially in capacitor (U = ½ CV²).
Transfers to inductor (magnetic).
Back to capacitor (opposite polarity).
Oscillations continue ideally.
Frequency:
➡️ f = 1/(2π sqrt(LC))
💡 Used in radio circuits, oscillators.
🔹 10. Transformers
Operate only with AC.
V2/V1 = N2/N1 (turns ratio).
Step-up: N2 > N1 → higher voltage.
Step-down: N2 < N1 → lower voltage.
Power ideally conserved: V1 I1 = V2 I2.
💡 Transmission lines use high voltage AC (to reduce I, minimize heat loss).
🔹 11. Phasor Representation (Expanded)
Phasors simplify AC analysis. Represent sinusoidal quantities as rotating vectors with angular velocity ω.
✔️ For resistor (R):
Current and voltage phasors are colinear (in phase).
✔️ For inductor (L):
Voltage phasor ahead of current by 90°.
Visual: Draw I along x-axis → V along +y-axis.
✔️ For capacitor (C):
Current ahead of voltage by 90°.
Visual: Draw V along x-axis → I along +y-axis.
✔️ For RLC series:
Voltage across R → along I.
Voltage across L → leads I by 90°.
Voltage across C → lags I by 90°.
Net voltage phasor: VR (along I) + (VL – VC) (along y-axis).
Impedance Z found by vector addition: Z = sqrt(R²+(XL – XC)²).
💡 Phasors give both magnitude and phase relationship. They are essential for resonance analysis and power factor calculations.
🔹 12. Power Factor in Detail
cosφ = R/Z.
Purely resistive → cosφ = 1 (best).
Purely inductive/capacitive → cosφ = 0 (no real power).
Typical industry circuits: φ ≠ 0 → need correction.
Correction: add capacitor banks to shift phase closer to resistive.
🔹 13. Applications of AC
✔️ AC generators → large scale electricity.
✔️ Transformers → high-voltage transmission.
✔️ Motors → use AC supply (induction motors).
✔️ Induction heating (eddy currents).
✔️ Communication systems (resonance).
✔️ Power factor correction in industries.
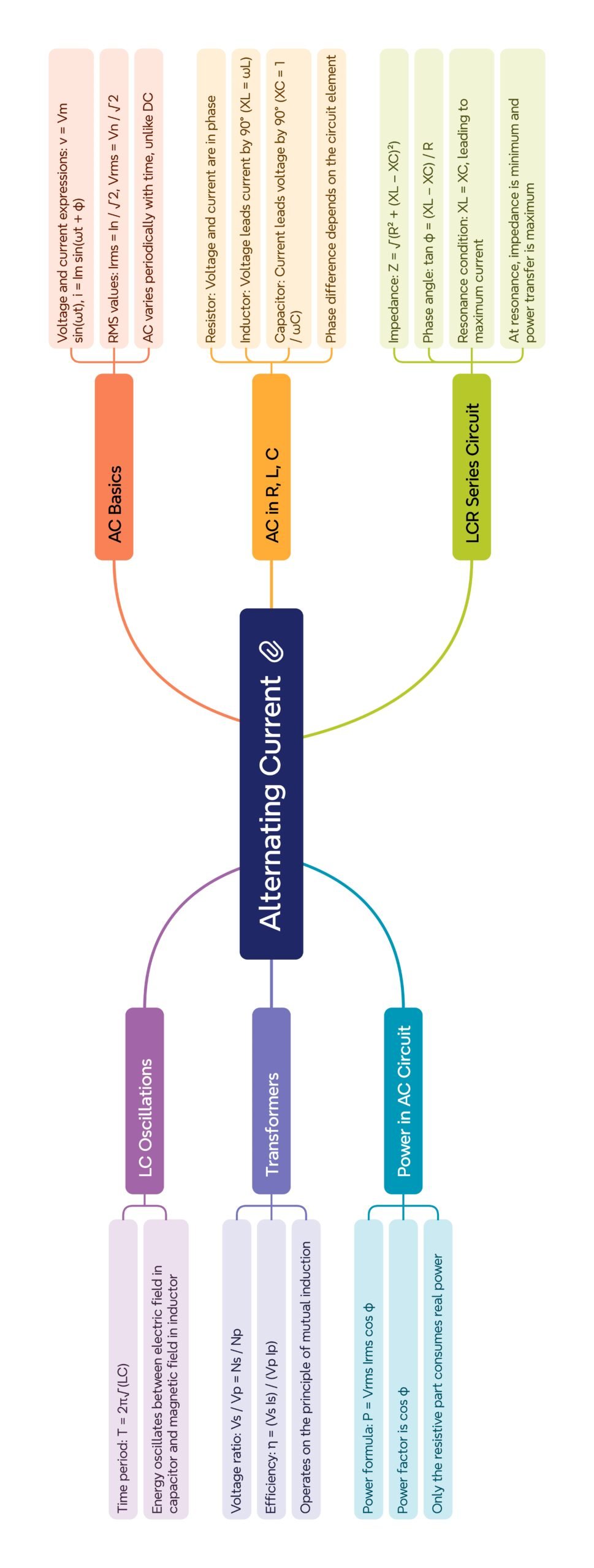
✨ Summary (~300 words)
Alternating current (AC): Varies sinusoidally with time, i(t) = I0 sin(ωt).
RMS values: Irms = I0/√2, Vrms = V0/√2.
Pure resistor: V and I in phase, power consumed continuously.
Pure inductor: Current lags voltage by 90°, reactance XL = ωL.
Pure capacitor: Current leads voltage by 90°, reactance XC = 1/(ωC).
RLC series circuit: Impedance Z = sqrt(R²+(XL – XC)²), phase tanφ = (XL – XC)/R.
Resonance: Occurs when XL = XC, frequency fr = 1/(2π√(LC)). Current maximum, Z = R.
Power in AC: Average power P = Vrms Irms cosφ, cosφ = power factor. Pure R consumes real power, pure L/C only exchange energy.
LC oscillations: Energy oscillates between capacitor (electric) and inductor (magnetic). Frequency f = 1/(2π√(LC)).
Transformers: Operate on mutual induction, step up or down AC voltages, essential in transmission.
Phasors: Vector representation of AC quantities. Voltage-current phase relations visualized → R (in phase), L (voltage leads 90°), C (current leads 90°).
Applications: Generators, transformers, motors, induction heating, resonance circuits, power factor correction.
📝 Quick Recap
🔵 AC: i = I0 sin(ωt), v = V0 sin(ωt).
🟢 RMS values: I0/√2, V0/√2.
🔴 R → I in phase, L → I lags, C → I leads.
🟡 Resonance at XL = XC, fr = 1/(2π√(LC)).
✔️ Power = Vrms Irms cosφ; transformers enable efficient transmission.
————————————————————————————————————————————————————————————————————————————
QUESTIONS FROM TEXTBOOK
Question 7.1
A 100 Ω resistor is connected to a 220 V, 50 Hz ac supply.
(a) What is the rms value of current in the circuit?
(b) What is the net power consumed over a full cycle?
Answer
✏️ Formula: I_rms = V_rms / R
➡️ I_rms = 220 / 100 = 2.2 A
✔️ RMS current = 2.2 A
✏️ Power: P = I_rms² × R
➡️ P = (2.2)² × 100 = 484 W
✔️ Net power consumed = 484 W
Question 7.2
(a) The peak voltage of an ac supply is 300 V. What is the rms voltage?
(b) The rms value of current in an ac circuit is 10 A. What is the peak current?
Answer
(a) ✏️ Vrms = V0 / √2
➡️ 300 / 1.414 = 212 V
✔️ RMS voltage = 212 V
(b) ✏️ I0 = √2 × Irms
➡️ 1.414 × 10 = 14.14 A
✔️ Peak current = 14.14 A
Question 7.3
A 44 mH inductor is connected to 220 V, 50 Hz ac supply. Determine the rms value of the current in the circuit.
Answer
✏️ XL = 2π f L
➡️ 2 × 3.14 × 50 × 0.044 = 13.82 Ω
✏️ Irms = V_rms / XL
➡️ 220 / 13.82 Ω = 15.9 A
✔️ RMS current = 15.9 A
Question 7.4
A 60 μF capacitor is connected to a 110 V, 60 Hz ac supply. Determine the rms value of the current in the circuit.
Answer
✏️ XC = 1 / (2π f C)
➡️ 1 / (2 × 3.14 × 60 × 60 × 10⁻⁶) = 44.2 Ω
✏️ Irms = V_rms / XC
➡️ 110 / 44.2 Ω = 2.49 A
✔️ RMS current = 2.49 A
Question 7.5
In Exercises 7.3 and 7.4, what is the net power absorbed by each circuit over a complete cycle? Explain your answer.
Answer
🔵 Inductor: Current lags 90°, average power = 0
🟢 Capacitor: Current leads 90°, average power = 0
✔️ Net power = 0 in both circuits, because L and C only store and release energy (reactive elements), not dissipate it.
Question 7.6
A charged 30 μF capacitor is connected to a 27 mH inductor. What is the angular frequency of free oscillations of the circuit?
Answer
✏️ ω = 1 / √(LC)
➡️ L = 27 × 10⁻³ H, C = 30 × 10⁻⁶ F
➡️ LC = 8.1 × 10⁻⁷
➡️ √(LC) = 9 × 10⁻⁴
✏️ ω = 1 / (9 × 10⁻⁴)
= 1111 rad/s
✔️ Angular frequency = 1.11 × 10³ rad/s
Question 7.7
A series LCR circuit with R = 20 Ω, L = 1.5 H and C = 35 μF is connected to a variable-frequency 200 V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transferred to the circuit in one complete cycle?
Answer
✏️ At resonance:
➡️ Impedance Z = R = 20 Ω
➡️ Irms = V_rms / R = 200 / 20 = 10 A
➡️ P = I² × R = 100 × 20 = 2000 W
✔️ Average power transferred = 2000 W
Question 7.8
Figure 7.17 shows a series LCR circuit connected to a variable frequency 230 V source. L = 5.0 H, C = 80 μF, R = 40 Ω.
(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
(c) Determine the rms potential drops across the three elements of the circuit. Show that the potential drop across the LC combination is zero at the resonating frequency.
Answer
(a) ✏️ fr = 1 / (2π √(LC))
➡️ = 1 / (2 × 3.14 × √(5 × 80 × 10⁻⁶))
➡️ = 1 / (6.28 × 0.02)
≈ 8 Hz
✔️ Resonant frequency = 8 Hz
(b) ✏️ At resonance: XL = XC → Z = R
➡️ Z = 40 Ω
➡️ Vrms = 230 V → V0 = √2 × 230 ≈ 325 V
➡️ I0 = V0 / R = 325 / 40 ≈ 8.1 A
✔️ Impedance = 40 Ω, Current amplitude = 8.1 A
(c) ✏️ Irms = Vrms / R = 230 / 40 = 5.75 A
VR = Irms × R = 230 V
VL = Irms × XL
VC = Irms × XC
💡 At resonance: XL = XC, so VL = VC.
➡️ These equal voltages cancel each other.
✔️ Net potential across LC = 0
✔️ Potential drop across R = 230 V
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS
(CBSE MODEL QUESTIONS PAPER)
ESPECIALLY MADE FROM THIS LESSON ONLY
Section A (MCQs: Q1–Q18)
Question 1
The RMS value of an AC with peak current 14 A is:
🔵 (A) 10 A
🟢 (B) 9.9 A
🟠 (C) 12 A
🔴 (D) 7 A
Answer
Irms = I0/√2 = 14/1.414 ≈ 9.9 A
✔️ Correct option: (B)
Question 2
In a pure resistor connected to AC source:
🔵 (A) Current lags voltage by 90°
🟢 (B) Current leads voltage by 90°
🟠 (C) Current and voltage are in phase
🔴 (D) Out of phase by 45°
Answer
✔️ In resistor, V and I are in phase.
Correct option: (C)
Question 3
For a pure inductor in AC:
🔵 (A) Voltage lags current by 90°
🟢 (B) Voltage leads current by 90°
🟠 (C) Current and voltage in phase
🔴 (D) Power consumed = maximum
Answer
✔️ Voltage leads current by 90°.
Correct option: (B)
Question 4
For a pure capacitor in AC, current:
🔵 (A) Lags voltage by 90°
🟢 (B) Leads voltage by 90°
🟠 (C) In phase with voltage
🔴 (D) Zero
Answer
✔️ Current leads by 90°.
Correct option: (B)
Question 5
Reactance of 100 μF capacitor at 50 Hz is:
🔵 (A) 31.8 Ω
🟢 (B) 318 Ω
🟠 (C) 3.18 Ω
🔴 (D) 0.318 Ω
Answer
XC = 1/(2π f C) = 1/(2×3.14×50×100×10⁻⁶) ≈ 31.8 Ω
✔️ Correct option: (A)
Question 6
Impedance of series RLC at resonance is:
🔵 (A) XL + XC
🟢 (B) R
🟠 (C) Zero
🔴 (D) Infinity
Answer
✔️ Z = R at resonance.
Correct option: (B)
Question 7
In series LCR resonance, current is:
🔵 (A) Minimum
🟢 (B) Zero
🟠 (C) Maximum
🔴 (D) Infinity
Answer
✔️ Current is maximum.
Correct option: (C)
Question 8
Power factor in pure resistive circuit:
🔵 (A) 0
🟢 (B) 1
🟠 (C) –1
🔴 (D) 0.5
Answer
✔️ cosφ = 1.
Correct option: (B)
Question 9
Power factor in purely reactive circuit (L or C):
🔵 (A) 0
🟢 (B) 1
🟠 (C) 0.5
🔴 (D) –1
Answer
✔️ cosφ = 0.
Correct option: (A)
Question 10
An inductor of 0.5 H is connected to 50 Hz AC supply. XL = ?
🔵 (A) 157 Ω
🟢 (B) 100 Ω
🟠 (C) 50 Ω
🔴 (D) 314 Ω
Answer
XL = 2π f L = 2×3.14×50×0.5 = 157 Ω
✔️ Correct option: (A)
Question 11
At resonance in RLC circuit:
🔵 (A) XL > XC
🟢 (B) XC > XL
🟠 (C) XL = XC
🔴 (D) Current = 0
Answer
✔️ Condition: XL = XC.
Correct option: (C)
Question 12
Power consumed in pure inductor is:
🔵 (A) Maximum
🟢 (B) Zero
🟠 (C) Vrms Irms
🔴 (D) None
Answer
✔️ Average power = 0.
Correct option: (B)
Question 13
A 50 Hz AC has angular frequency:
🔵 (A) 314 rad/s
🟢 (B) 157 rad/s
🟠 (C) 628 rad/s
🔴 (D) 100 rad/s
Answer
ω = 2π f = 2×3.14×50 = 314 rad/s
✔️ Correct option: (A)
Question 14
If Vrms = 220 V, then V0 = ?
🔵 (A) 220 V
🟢 (B) 311 V
🟠 (C) 110 V
🔴 (D) 155 V
Answer
V0 = √2 × Vrms = 1.414×220 = 311 V
✔️ Correct option: (B)
Question 15
Which device uses resonance?
🔵 (A) Transformer
🟢 (B) Radio tuning circuit
🟠 (C) Rectifier
🔴 (D) Electric heater
Answer
✔️ Radio tuning → resonance principle.
Correct option: (B)
Question 16
LC oscillations involve:
🔵 (A) Exchange of energy between R and L
🟢 (B) Exchange of energy between C and L
🟠 (C) Energy loss as heat
🔴 (D) None
Answer
✔️ Energy oscillates between capacitor & inductor.
Correct option: (B)
Question 17
Power factor = cosφ = R/Z. If φ = 0°, then?
🔵 (A) 0
🟢 (B) 1
🟠 (C) 0.5
🔴 (D) None
Answer
✔️ cos0° = 1.
Correct option: (B)
Question 18
The unit of reactance is:
🔵 (A) Ampere
🟢 (B) Ohm
🟠 (C) Volt
🔴 (D) Weber
Answer
✔️ Same as resistance = ohm.
Correct option: (B)
Section B (Q19–Q23: Short Answers)
Question 19
Define RMS value of AC current. Derive relation with peak current.
Answer
✏️ Irms = sqrt[(1/T) ∫0^T i² dt] = I0/√2
✔️ Irms = I0 / √2
Question 20
Phase difference between current and voltage?
Answer
Resistor → 0°
Inductor → –90° (current lags)
Capacitor → +90° (current leads)
Question 21
What is power factor?
Answer
✏️ Power factor = cosφ = R/Z
✔️ Significance: Determines efficiency of power transfer, improved with capacitors.
Question 22
What is resonance?
Answer
Resonance in LCR when XL = XC → impedance minimum = R → current maximum.
✔️ Frequency: fr = 1/(2π√(LC))
Question 23
Why transformer works with AC only?
Answer
✔️ Transformer depends on changing flux.
AC → changing flux → induced emf.
DC → constant flux → no emf.
Section C (Q24–Q28: Mid-Length)
Question 24
200 V, 50 Hz applied to 100 Ω resistor. Find:
(a) Peak voltage (b) Peak current
Answer
➡️ V0 = √2 Vrms = 283 V
➡️ Irms = 200/100 = 2 A → I0 = 2.83 A
✔️ V0 = 283 V, I0 = 2.83 A
Question 25
L = 0.1 H, 240 V, 50 Hz → Find XL & Irms.
Answer
➡️ XL = 2π f L = 31.4 Ω
➡️ Irms = 240/31.4 = 7.64 A
✔️ XL = 31.4 Ω, Irms = 7.64 A
Question 26
Find fr for L = 0.1 H, C = 25 μF.
Answer
➡️ fr = 1/(2π√(LC)) ≈ 1008 Hz
✔️ fr = 1008 Hz
Question 27
Explain LC oscillations.
Answer
✔️ Energy oscillates between capacitor (electric) and inductor (magnetic).
Frequency f = 1/(2π√(LC))
Question 28
50 μF capacitor, 200 V, 50 Hz → Find XC & Irms.
Answer
➡️ XC = 63.7 Ω
➡️ Irms = 200/63.7 = 3.14 A
✔️ XC = 63.7 Ω, Irms = 3.14 A
Section D (Q29–Q31: Long Answers, with Phasor Descriptions)
Question 29
Derive expression for impedance of RLC series circuit.
Answer
Voltage across R: IR (in phase with current).
Voltage across L: IXL (leads by +90°).
Voltage across C: IXC (lags by –90°).
💡 Phasor description:
Take IR on horizontal axis. VL upward, VC downward. Net vertical component = VL – VC. Total voltage = phasor sum of IR (horizontal) and (VL–VC) (vertical).
➡️ V² = (IR)² + (I(XL–XC))²
➡️ Z = V/I = √(R²+(XL–XC)²)
✔️ Z = √(R²+(XL–XC)²)
Question 30
Derive expression for average power in AC circuit.
Answer
v = V0 sinωt, i = I0 sin(ωt–φ)
Instantaneous power p = V0 I0 sin(ωt) sin(ωt–φ)
💡 Phasor description:
Current as reference. Voltage makes angle φ. Component of V along current axis = V cosφ → responsible for real power.
➡️ Average power = Vrms Irms cosφ
✔️ Pavg = Vrms × Irms × cosφ
Question 31
Resonance and resonant frequency in LCR circuit.
Answer
Resonance when XL = XC → current maximum.
💡 Phasor description:
At resonance, VL = VC → cancel out. Net voltage = VR only → Z = R.
➡️ ω² = 1/(LC)
➡️ fr = 1/(2π√(LC))
✔️ Resonant frequency derived.
Section E (Q32–Q33: Extended Numericals)
Question 32
230 V, 50 Hz supply to 40 Ω resistor + 80 μF capacitor. Find:
(a) Z (b) Irms (c) Power
Answer
➡️ XC = 39.8 Ω
➡️ Z = √(40²+39.8²) = 56.4 Ω
➡️ Irms = 230/56.4 = 4.08 A
➡️ cosφ = 40/56.4 = 0.71
➡️ P = 230×4.08×0.71 ≈ 667 W
✔️ Z = 56.4 Ω, Irms = 4.08 A, P = 667 W
Question 33
Series LCR: R = 10 Ω, L = 0.1 H, C = 100 μF, Vrms = 200 V, f = 50 Hz. Find:
(a) XL, XC (b) Z (c) I (d) Power
Answer
➡️ XL = 31.4 Ω, XC = 31.8 Ω
➡️ Z = √(10²+(31.4–31.8)²) = 10.0 Ω
➡️ I = 200/10 = 20 A
➡️ cosφ = R/Z = 1
➡️ P = 200×20×1 = 4000 W
✔️ XL = 31.4 Ω, XC = 31.8 Ω, Z = 10 Ω, I = 20 A, P = 4000 W
————————————————————————————————————————————————————————————————————————————
NEET QUESTIONS FROM THIS LESSON
Question 1: The rms value of current for an AC of peak value 10 A is
🔵 (A) 10 A
🟢 (B) 7.07 A
🟠 (C) 5 A
🔴 (D) 14.14 A
Answer: (B) 7.07 A
Year: 2025
Question 2: The average power consumed in a pure inductive circuit over one complete cycle is
🔵 (A) maximum
🟢 (B) half of maximum
🟠 (C) zero
🔴 (D) minimum
Answer: (C) zero
Year: 2025
Question 3: A capacitor of capacitance C is connected to AC source of frequency f. The capacitive reactance is
🔵 (A) 1/2πfC
🟢 (B) 2πfC
🟠 (C) f/C
🔴 (D) C/f
Answer: (A) 1/2πfC
Year: 2025
Question 4: In an AC circuit, the phase difference between current and voltage in a pure resistor is
🔵 (A) 90°
🟢 (B) 0°
🟠 (C) 180°
🔴 (D) 45°
Answer: (B) 0°
Year: 2024
Question 5: The Q-factor of a series LCR circuit is given by
🔵 (A) ωL/R
🟢 (B) R/ωL
🟠 (C) ωCR
🔴 (D) 1/ωCR
Answer: (A) ωL/R
Year: 2024
Question 6: In a series LCR circuit at resonance, the impedance is
🔵 (A) maximum
🟢 (B) minimum
🟠 (C) infinite
🔴 (D) equal to inductive reactance
Answer: (B) minimum
Year: 2024
Question 7: In a purely capacitive circuit, current leads the voltage by
🔵 (A) 0°
🟢 (B) 90°
🟠 (C) 180°
🔴 (D) 45°
Answer: (B) 90°
Year: 2024
Question 8: A choke coil is basically a
🔵 (A) pure capacitor
🟢 (B) pure inductor
🟠 (C) pure resistor
🔴 (D) combination of RLC
Answer: (B) pure inductor
Year: 2023
Question 9: In a transformer, power loss can be minimized by
🔵 (A) thick copper wire and laminated core
🟢 (B) increasing number of turns
🟠 (C) using air core
🔴 (D) reducing voltage
Answer: (A) thick copper wire and laminated core
Year: 2023
Question 10: In a purely inductive AC circuit, the current lags voltage by
🔵 (A) 0°
🟢 (B) 90°
🟠 (C) 180°
🔴 (D) 45°
Answer: (B) 90°
Year: 2023
Question 11: In a resonance LCR circuit, power factor is
🔵 (A) 0
🟢 (B) 1
🟠 (C) ∞
🔴 (D) ½
Answer: (B) 1
Year: 2023
Question 12: The average value of alternating current over one complete cycle is
🔵 (A) maximum
🟢 (B) zero
🟠 (C) rms value
🔴 (D) peak value
Answer: (B) zero
Year: 2022
Question 13: In an ideal transformer, efficiency is
🔵 (A) 100%
🟢 (B) 50%
🟠 (C) 75%
🔴 (D) 0%
Answer: (A) 100%
Year: 2022
Question 14: A 50 Hz AC has angular frequency equal to
🔵 (A) 100 rad/s
🟢 (B) 157 rad/s
🟠 (C) 314 rad/s
🔴 (D) 628 rad/s
Answer: (C) 314 rad/s
Year: 2022
Question 15: The average power consumed in a pure resistive AC circuit is
🔵 (A) zero
🟢 (B) Vrms × Irms
🟠 (C) ½ V × I
🔴 (D) depends on phase
Answer: (B) Vrms × Irms
Year: 2022
Question 16: The impedance of a series LCR circuit at resonance is
🔵 (A) R
🟢 (B) L
🟠 (C) C
🔴 (D) zero
Answer: (A) R
Year: 2021
Question 17: In AC circuits, wattless current exists in
🔵 (A) resistive
🟢 (B) inductive
🟠 (C) resistive-inductive
🔴 (D) none
Answer: (B) inductive
Year: 2021
Question 18: The potential difference across pure inductor in AC circuit leads the current by
🔵 (A) 0°
🟢 (B) 90°
🟠 (C) 180°
🔴 (D) 270°
Answer: (B) 90°
Year: 2021
Question 19: In a series LCR circuit, at resonance
🔵 (A) XL = XC
🟢 (B) XL > XC
🟠 (C) XL < XC
🔴 (D) XL = 0
Answer: (A) XL = XC
Year: 2021
Question 20: In a purely capacitive circuit supplied by AC, the power consumed is
🔵 (A) maximum
🟢 (B) zero
🟠 (C) VrmsIrms
🔴 (D) depends on frequency
Answer: (B) zero
Year: 2020
Question 21: The inductive reactance is given by
🔵 (A) XL = 2πfL
🟢 (B) XL = 1/2πfL
🟠 (C) XL = f/L
🔴 (D) XL = L/f
Answer: (A) XL = 2πfL
Year: 2020
Question 22: In a choke coil, loss of energy occurs due to
🔵 (A) inductance
🟢 (B) resistance of coil wire
🟠 (C) capacitance
🔴 (D) none
Answer: (B) resistance of coil wire
Year: 2020
Question 23: The RMS value of current in 10 A peak AC is
🔵 (A) 5 A
🟢 (B) 7.07 A
🟠 (C) 10 A
🔴 (D) 14.14 A
Answer: (B) 7.07 A
Year: 2020
Question 24: In a purely resistive AC circuit, current and voltage are
🔵 (A) in phase
🟢 (B) out of phase by 90°
🟠 (C) out of phase by 180°
🔴 (D) out of phase by 45°
Answer: (A) in phase
Year: 2019
Question 25: In a transformer, the core is laminated to reduce
🔵 (A) hysteresis loss
🟢 (B) eddy current loss
🟠 (C) copper loss
🔴 (D) flux leakage
Answer: (B) eddy current loss
Year: 2019
Question 26: The sharpness of resonance of an LCR circuit is measured by
🔵 (A) impedance
🟢 (B) Q-factor
🟠 (C) resistance
🔴 (D) frequency
Answer: (B) Q-factor
Year: 2019
Question 27: The value of power factor in a pure resistive circuit is
🔵 (A) 0
🟢 (B) 1
🟠 (C) ∞
🔴 (D) ½
Answer: (B) 1
Year: 2019
Question 28: The average power consumed in a pure inductive AC circuit is
🔵 (A) Vrms Irms
🟢 (B) ½ VI
🟠 (C) 0
🔴 (D) maximum
Answer: (C) 0
Year: 2018
Question 29: In an AC circuit, if phase angle between current and voltage is 90°, then power factor is
🔵 (A) 0
🟢 (B) 1
🟠 (C) ½
🔴 (D) ∞
Answer: (A) 0
Year: 2018
Question 30: In a purely resistive AC circuit, instantaneous current is i = I₀ sin ωt, voltage is
🔵 (A) V = V₀ sin ωt
🟢 (B) V = V₀ cos ωt
🟠 (C) V = V₀ sin (ωt + π/2)
🔴 (D) V = V₀ sin (ωt − π/2)
Answer: (A) V = V₀ sin ωt
Year: 2018
Question 31: In a series LCR circuit, if Q = 100, the bandwidth is
🔵 (A) f₀
🟢 (B) f₀/100
🟠 (C) 100 f₀
🔴 (D) 0
Answer: (B) f₀/100
Year: 2017
Question 32: If a transformer steps up voltage, it
🔵 (A) increases power
🟢 (B) decreases current
🟠 (C) increases current
🔴 (D) decreases frequency
Answer: (B) decreases current
Year: 2017
Question 33: The RMS value of an AC is related to its peak value by
🔵 (A) I₀/√2
🟢 (B) I₀ × √2
🟠 (C) I₀/2
🔴 (D) I₀
Answer: (A) I₀/√2
Year: 2017
Question 34: In an AC circuit, average value of current over half cycle is
🔵 (A) zero
🟢 (B) 2I₀/π
🟠 (C) I₀/√2
🔴 (D) I₀
Answer: (B) 2I₀/π
Year: 2017
Question 35: In a pure capacitive circuit, power factor is
🔵 (A) 0
🟢 (B) 1
🟠 (C) ∞
🔴 (D) ½
Answer: (A) 0
Year: 2016
Question 36: In a pure resistive circuit, power consumed is
🔵 (A) I²R
🟢 (B) 0
🟠 (C) Irms × Vrms × cos φ
🔴 (D) depends on frequency
Answer: (A) I²R
Year: 2016
Question 37: A choke coil works on the principle of
🔵 (A) capacitance
🟢 (B) inductance
🟠 (C) resistance
🔴 (D) resonance
Answer: (B) inductance
Year: 2016
Question 38: In a transformer, the frequency of primary and secondary voltages is
🔵 (A) same
🟢 (B) different
🟠 (C) half
🔴 (D) double
Answer: (A) same
Year: 2015
Question 39: The power factor of an AC circuit is cos φ = R/Z. For purely inductive circuit it is
🔵 (A) 0
🟢 (B) 1
🟠 (C) ½
🔴 (D) ∞
Answer: (A) 0
Year: 2015
Question 40: The time average power in an AC circuit is
🔵 (A) Vrms Irms cos φ
🟢 (B) VI
🟠 (C) VI/2
🔴 (D) 0
Answer: (A) Vrms Irms cos φ
Year: 2015
Question 41: In a series LCR circuit, impedance is
🔵 (A) √(R² + (XL − XC)²)
🟢 (B) R + XL + XC
🟠 (C) XL + XC
🔴 (D) R − (XL + XC)
Answer: (A) √(R² + (XL − XC)²)
Year: 2014
Question 42: A capacitor of 10 μF is connected to 200 V, 50 Hz AC. Its reactance is
🔵 (A) 31.8 Ω
🟢 (B) 318 Ω
🟠 (C) 0.318 Ω
🔴 (D) 3.18 Ω
Answer: (B) 318 Ω
Year: 2014
Question 43: A 220 V AC is applied to pure resistor 100 Ω. Power consumed is
🔵 (A) 220 W
🟢 (B) 484 W
🟠 (C) 2200 W
🔴 (D) 4840 W
Answer: (B) 484 W
Year: 2013
Question 44: In an AC circuit, instantaneous emf is e = 200 sin 314t. The frequency is
🔵 (A) 314 Hz
🟢 (B) 50 Hz
🟠 (C) 100 Hz
🔴 (D) 200 Hz
Answer: (B) 50 Hz
Year: 2013
Question 45: A device which allows AC but blocks DC is
🔵 (A) resistor
🟢 (B) inductor
🟠 (C) capacitor
🔴 (D) transformer
Answer: (C) capacitor
Year: 2012
Question 46: A 60 Hz AC has time period equal to
🔵 (A) 0.0167 s
🟢 (B) 0.017 s
🟠 (C) 0.015 s
🔴 (D) 0.020 s
Answer: (A) 0.0167 s
Year: 2012
Question 47: The reactance of a 10 H inductor in 50 Hz AC is
🔵 (A) 3140 Ω
🟢 (B) 500 Ω
🟠 (C) 1570 Ω
🔴 (D) 1000 Ω
Answer: (A) 3140 Ω
Year: 2011
Question 48: The average value of AC over half cycle is
🔵 (A) 0
🟢 (B) 2I₀/π
🟠 (C) I₀/2
🔴 (D) I₀/√2
Answer: (B) 2I₀/π
Year: 2010
Question 49: The effective resistance of LCR circuit at resonance is
🔵 (A) XL + XC
🟢 (B) XL − XC
🟠 (C) R
🔴 (D) 0
Answer: (C) R
Year: 2009
Question 50: The equation of current in AC circuit is i = I₀ sin ωt. The rms value is
🔵 (A) I₀
🟢 (B) I₀/2
🟠 (C) I₀/√2
🔴 (D) 2I₀
Answer: (C) I₀/√2
Year: 2008
————————————————————————————————————————————————————————————————————————————
JEE MAINS QUESTIONS FROM THIS LESSON
Question 1: The average power in an AC circuit is maximum when phase difference between current and voltage is
🔵 (A) 0°
🟢 (B) 45°
🟠 (C) 90°
🔴 (D) 180°
Answer: (A) 0°
Year: 2025 | Shift 1
Question 2: In an AC circuit, current leads voltage by 90°. The circuit contains
🔵 (A) pure resistor
🟢 (B) pure inductor
🟠 (C) pure capacitor
🔴 (D) L and R both
Answer: (C) pure capacitor
Year: 2025 | Shift 2
Question 3: A 220 V, 50 Hz AC supply is connected to a 110 Ω resistor. The rms current is
🔵 (A) 1 A
🟢 (B) 2 A
🟠 (C) 3 A
🔴 (D) 5 A
Answer: (B) 2 A
Year: 2024 | Jan Shift 1
Question 4: The reactance of a capacitor of capacitance C in AC circuit is
🔵 (A) 1/ωC
🟢 (B) ωC
🟠 (C) C/ω
🔴 (D) ω/C
Answer: (A) 1/ωC
Year: 2024 | Apr Shift 1
Question 5: In an LCR series circuit at resonance, the power factor is
🔵 (A) 0
🟢 (B) 0.5
🟠 (C) 1
🔴 (D) ∞
Answer: (C) 1
Year: 2024 | Jan Shift 2
Question 6: The quality factor (Q-factor) of an LCR circuit is given by
🔵 (A) ω₀L/R
🟢 (B) R/ω₀L
🟠 (C) ω₀RC
🔴 (D) 1/ω₀RC
Answer: (A) ω₀L/R
Year: 2024 | Apr Shift 2
Question 7: In an AC circuit, the average value of current over one complete cycle is
🔵 (A) I₀/√2
🟢 (B) zero
🟠 (C) I₀
🔴 (D) 2I₀/π
Answer: (B) zero
Year: 2023 | Apr Shift 1
Question 8: In a purely inductive circuit, the power consumed is
🔵 (A) VI
🟢 (B) ½ VI
🟠 (C) zero
🔴 (D) V²/R
Answer: (C) zero
Year: 2023 | Jan Shift 1
Question 9: The rms value of an alternating current I = I₀ sinωt is
🔵 (A) I₀
🟢 (B) I₀/√2
🟠 (C) I₀/2
🔴 (D) I₀/π
Answer: (B) I₀/√2
Year: 2023 | Apr Shift 2
Question 10: The resonance frequency of an LCR circuit is given by
🔵 (A) 1/2π√LC
🟢 (B) 1/2π√(L/C)
🟠 (C) 1/2π√(C/L)
🔴 (D) 1/2πLC
Answer: (A) 1/2π√LC
Year: 2022 | Jun Shift 1
Question 11: The phase difference between voltage and current in a purely resistive circuit is
🔵 (A) 0°
🟢 (B) 90°
🟠 (C) 180°
🔴 (D) 45°
Answer: (A) 0°
Year: 2022 | Jul Shift 1
Question 12: In a purely capacitive circuit supplied by AC source, the current is
🔵 (A) in phase with voltage
🟢 (B) lagging behind voltage
🟠 (C) leading voltage by 90°
🔴 (D) lagging by 180°
Answer: (C) leading voltage by 90°
Year: 2022 | Jul Shift 2
Question 13: The power factor of a pure resistor is
🔵 (A) 0
🟢 (B) 0.5
🟠 (C) 1
🔴 (D) ∞
Answer: (C) 1
Year: 2022 | Jun Shift 2
Question 14: A 50 Hz AC voltage is applied to a capacitor of 100 μF. The capacitive reactance is
🔵 (A) 31.8 Ω
🟢 (B) 50 Ω
🟠 (C) 100 Ω
🔴 (D) 159 Ω
Answer: (A) 31.8 Ω
Year: 2021 | Mar Shift 1
Question 15: In an AC circuit, if I = I₀ sin(ωt + φ), then φ is called
🔵 (A) phase constant
🟢 (B) phase lag
🟠 (C) phase angle
🔴 (D) both A and C
Answer: (D) both A and C
Year: 2021 | Feb Shift 1
Question 16: The impedance of an RLC circuit is minimum at
🔵 (A) ω = 0
🟢 (B) ω = ∞
🟠 (C) resonance
🔴 (D) none
Answer: (C) resonance
Year: 2021 | Jul Shift 2
Question 17: In a series LCR circuit at resonance, current is
🔵 (A) maximum
🟢 (B) minimum
🟠 (C) zero
🔴 (D) depends on L
Answer: (A) maximum
Year: 2021 | Mar Shift 2
Question 18: The instantaneous power in AC circuit is given by
🔵 (A) VI sin²ωt
🟢 (B) VI cos²ωt
🟠 (C) VI cosφ
🔴 (D) VI sinωt cosωt
Answer: (A) VI sin²ωt
Year: 2020 | Jan Shift 1
Question 19: A 220 V AC supply is connected to 220 Ω resistor. The rms current is
🔵 (A) 0.5 A
🟢 (B) 1 A
🟠 (C) 2 A
🔴 (D) 5 A
Answer: (B) 1 A
Year: 2020 | Sept Shift 2
Question 20: In an AC circuit, average power is
🔵 (A) Vrms Irms cosφ
🟢 (B) V₀I₀
🟠 (C) Vrms Irms
🔴 (D) zero
Answer: (A) Vrms Irms cosφ
Year: 2020 | Sept Shift 1
Question 21: In a pure inductive circuit, current lags behind voltage by
🔵 (A) 0°
🟢 (B) 90°
🟠 (C) 180°
🔴 (D) 270°
Answer: (B) 90°
Year: 2019 | Jan Shift 1
Question 22: In a circuit with resistance R and inductance L, time constant is
🔵 (A) R/L
🟢 (B) L/R
🟠 (C) √(L/R)
🔴 (D) √(R/L)
Answer: (B) L/R
Year: 2019 | Apr Shift 2
Question 23: The resonant frequency of LCR circuit increases if
🔵 (A) L increases
🟢 (B) C decreases
🟠 (C) both L and C increase
🔴 (D) R increases
Answer: (B) C decreases
Year: 2019 | Jan Shift 2
Question 24: In an AC circuit, current lags voltage by angle φ. The circuit likely contains
🔵 (A) inductance
🟢 (B) capacitance
🟠 (C) resistance
🔴 (D) pure conductor
Answer: (A) inductance
Year: 2018
Question 25: The effective value of AC current is 5 A. Its peak value is
🔵 (A) 5 A
🟢 (B) 5√2 A
🟠 (C) 10 A
🔴 (D) 2.5 A
Answer: (B) 5√2 A
Year: 2018
Question 26: In an AC circuit with Vrms = 200 V, Irms = 4 A, and power factor 0.5, the average power consumed is
🔵 (A) 200 W
🟢 (B) 300 W
🟠 (C) 400 W
🔴 (D) 800 W
Answer: (C) 400 W
Year: 2018
Question 27: A 50 Hz AC is applied to a 1 μF capacitor. The capacitive reactance is
🔵 (A) 3180 Ω
🟢 (B) 1590 Ω
🟠 (C) 1000 Ω
🔴 (D) 500 Ω
Answer: (A) 3180 Ω
Year: 2017
Question 28: The rms voltage across an inductor in a series LCR circuit at resonance is
🔵 (A) equal to applied voltage
🟢 (B) less than applied voltage
🟠 (C) greater than applied voltage
🔴 (D) zero
Answer: (C) greater than applied voltage
Year: 2017
Question 29: In a purely capacitive AC circuit, the current
🔵 (A) lags voltage by 90°
🟢 (B) leads voltage by 90°
🟠 (C) in phase with voltage
🔴 (D) zero
Answer: (B) leads voltage by 90°
Year: 2017
Question 30: In a pure resistive circuit, the average power is
🔵 (A) Vrms × Irms
🟢 (B) V₀I₀/2
🟠 (C) VI cosφ
🔴 (D) all of these
Answer: (D) all of these
Year: 2016
Question 31: A choke coil works on the principle of
🔵 (A) capacitance
🟢 (B) inductance
🟠 (C) resistance
🔴 (D) resonance
Answer: (B) inductance
Year: 2016
Question 32: The impedance of a series LCR circuit at resonance is
🔵 (A) minimum = R
🟢 (B) maximum = R
🟠 (C) zero
🔴 (D) infinite
Answer: (A) minimum = R
Year: 2016
Question 33: In an LCR circuit, if inductive reactance = capacitive reactance, then the circuit is
🔵 (A) resistive
🟢 (B) capacitive
🟠 (C) inductive
🔴 (D) non-conducting
Answer: (A) resistive
Year: 2015
Question 34: The expression for impedance in LCR series circuit is
🔵 (A) √(R² + (XL + XC)²)
🟢 (B) √(R² + (XL − XC)²)
🟠 (C) XL + XC + R
🔴 (D) R + XL − XC
Answer: (B) √(R² + (XL − XC)²)
Year: 2015
Question 35: A capacitor of 100 μF is connected across 220 V, 50 Hz supply. The rms current is
🔵 (A) 6.9 A
🟢 (B) 5.5 A
🟠 (C) 7.0 A
🔴 (D) 1.1 A
Answer: (A) 6.9 A
Year: 2015
Question 36: A pure inductor of 0.1 H is connected to 220 V, 50 Hz supply. The rms current is
🔵 (A) 4.5 A
🟢 (B) 5.0 A
🟠 (C) 7.0 A
🔴 (D) 8.5 A
Answer: (C) 7.0 A
Year: 2014
Question 37: The expression for resonance frequency in LCR circuit is
🔵 (A) 1/2π√(LC)
🟢 (B) 1/2π√(L/C)
🟠 (C) 1/2π√(C/L)
🔴 (D) 1/2πLC
Answer: (A) 1/2π√(LC)
Year: 2014
Question 38: In a pure resistive AC circuit, the current is
🔵 (A) in phase with voltage
🟢 (B) lags behind voltage by 90°
🟠 (C) leads voltage by 90°
🔴 (D) opposite to voltage
Answer: (A) in phase with voltage
Year: 2014
Question 39: The rms value of a triangular current wave of peak value I₀ is
🔵 (A) I₀/√2
🟢 (B) I₀/√3
🟠 (C) I₀/2
🔴 (D) I₀
Answer: (B) I₀/√3
Year: 2013
Question 40: In a purely capacitive circuit, the current is maximum when
🔵 (A) frequency is low
🟢 (B) frequency is high
🟠 (C) independent of frequency
🔴 (D) none
Answer: (B) frequency is high
Year: 2013
Question 41: In a pure inductor, average power consumed in one cycle is
🔵 (A) VI
🟢 (B) zero
🟠 (C) VI/2
🔴 (D) depends on frequency
Answer: (B) zero
Year: 2012 (AIEEE)
Question 42: A circuit contains a capacitor only. The current leads the voltage by
🔵 (A) 0°
🟢 (B) 90°
🟠 (C) 180°
🔴 (D) 270°
Answer: (B) 90°
Year: 2012 (AIEEE)
Question 43: A 50 Hz AC voltage is applied to a 10 mH inductor. The inductive reactance is
🔵 (A) 3.14 Ω
🟢 (B) 6.28 Ω
🟠 (C) 31.4 Ω
🔴 (D) 314 Ω
Answer: (C) 31.4 Ω
Year: 2011 (AIEEE)
Question 44: The average value of AC over half cycle is
🔵 (A) 2I₀/π
🟢 (B) I₀/√2
🟠 (C) I₀/2
🔴 (D) zero
Answer: (A) 2I₀/π
Year: 2011 (AIEEE)
Question 45: The ratio of rms value to average value of sinusoidal current is
🔵 (A) 1.11
🟢 (B) 1.0
🟠 (C) 0.9
🔴 (D) 1.57
Answer: (A) 1.11
Year: 2010 (AIEEE)
Question 46: In AC circuit, power factor cosφ =
🔵 (A) R/Z
🟢 (B) Z/R
🟠 (C) XL/XC
🔴 (D) XC/XL
Answer: (A) R/Z
Year: 2010 (AIEEE)
Question 47: A 220 V, 50 Hz AC is applied to pure capacitor of 10 μF. The rms current is
🔵 (A) 0.69 A
🟢 (B) 1.1 A
🟠 (C) 2.2 A
🔴 (D) 3.5 A
Answer: (C) 2.2 A
Year: 2009 (AIEEE)
Question 48: In resonance condition, the impedance of an LCR series circuit is
🔵 (A) XL − XC
🟢 (B) XL + XC
🟠 (C) R
🔴 (D) 0
Answer: (C) R
Year: 2009 (AIEEE)
Question 49: A 100 V AC is applied to pure resistor of 50 Ω. The peak current is
🔵 (A) 2 A
🟢 (B) √2 A
🟠 (C) 4 A
🔴 (D) 2√2 A
Answer: (D) 2√2 A
Year: 2008 (AIEEE)
Question 50: In a pure capacitive AC circuit, the current is
🔵 (A) in phase with voltage
🟢 (B) lagging voltage by 90°
🟠 (C) leading voltage by 90°
🔴 (D) opposite to voltage
Answer: (C) leading voltage by 90°
Year: 2007 (AIEEE)
————————————————————————————————————————————————————————————————————————————
JEE ADVANCED QUESTIONS FROM THIS LESSON
Question 1: In a purely resistive AC circuit, the phase difference between current and voltage is
🔵 (A) 0°
🟢 (B) 90°
🟠 (C) 180°
🔴 (D) 45°
Answer: (A) 0°
Year: 2023 | Paper 1
Question 2: The rms value of current in AC circuit with peak current 10 A is
🔵 (A) 5 A
🟢 (B) 7.07 A
🟠 (C) 10√2 A
🔴 (D) 20 A
Answer: (B) 7.07 A
Year: 2023 | Paper 1
Question 3: In an AC circuit with only inductor, the current
🔵 (A) leads voltage by 90°
🟢 (B) lags voltage by 90°
🟠 (C) is in phase
🔴 (D) opposite in phase
Answer: (B) lags voltage by 90°
Year: 2022 | Paper 1
Question 4: In an AC circuit with capacitor only, current
🔵 (A) leads voltage by 90°
🟢 (B) lags voltage by 90°
🟠 (C) in phase
🔴 (D) opposite
Answer: (A) leads voltage by 90°
Year: 2022 | Paper 1
Question 5: Power factor of pure resistor circuit is
🔵 (A) 0
🟢 (B) 1
🟠 (C) between 0 and 1
🔴 (D) infinite
Answer: (B) 1
Year: 2021 | Paper 1
Question 6: The average power over one complete cycle in a pure inductive circuit is
🔵 (A) zero
🟢 (B) maximum
🟠 (C) half of maximum
🔴 (D) finite
Answer: (A) zero
Year: 2021 | Paper 1
Question 7: In a series RLC circuit at resonance, the impedance is equal to
🔵 (A) XL
🟢 (B) XC
🟠 (C) R
🔴 (D) √(XL^2 + R^2)
Answer: (C) R
Year: 2020 | Paper 1
Question 8: In a transformer, power is lost due to
🔵 (A) eddy currents
🟢 (B) hysteresis
🟠 (C) resistance of windings
🔴 (D) all of these
Answer: (D) all of these
Year: 2020 | Paper 1
Question 9: In an AC circuit, the instantaneous emf is e = 200 sin(100πt). The frequency is
🔵 (A) 25 Hz
🟢 (B) 50 Hz
🟠 (C) 100 Hz
🔴 (D) 200 Hz
Answer: (B) 50 Hz
Year: 2019 | Paper 1
Question 10: In an AC circuit, instantaneous voltage is v = 220√2 sin(100πt). The rms voltage is
🔵 (A) 220 V
🟢 (B) 110 V
🟠 (C) 311 V
🔴 (D) 440 V
Answer: (A) 220 V
Year: 2019 | Paper 1
Question 11: Quality factor of a series resonant circuit is given by
🔵 (A) R/ωL
🟢 (B) ωL/R
🟠 (C) 1/ωCR
🔴 (D) 1/RC
Answer: (B) ωL/R
Year: 2018 | Paper 1
Question 12: In an AC circuit with resistor R, inductor L and capacitor C in series, the power factor is
🔵 (A) R/Z
🟢 (B) Z/R
🟠 (C) XL/Z
🔴 (D) XC/Z
Answer: (A) R/Z
Year: 2018 | Paper 1
Question 13: In a purely capacitive AC circuit, the average power consumption is
🔵 (A) 0
🟢 (B) maximum
🟠 (C) half of maximum
🔴 (D) infinite
Answer: (A) 0
Year: 2017 | Paper 1
Question 14: In an RLC series circuit, at resonance the current is
🔵 (A) minimum
🟢 (B) maximum
🟠 (C) zero
🔴 (D) infinite
Answer: (B) maximum
Year: 2017 | Paper 1
Question 15: In an AC circuit containing pure resistance, the current is I = I0 sin(ωt). The power dissipated is
🔵 (A) I0^2 R / 2
🟢 (B) I0^2 R
🟠 (C) I0^2 / R
🔴 (D) 0
Answer: (A) I0^2 R / 2
Year: 2016 | Paper 1
Question 16: In an AC circuit with applied emf E = E0 sin(ωt), the average value of emf over one cycle is
🔵 (A) 0
🟢 (B) 2E0/π
🟠 (C) E0/√2
🔴 (D) E0
Answer: (A) 0
Year: 2016 | Paper 1
Question 17: The instantaneous current in an AC circuit is i = 10 sin(314t). The frequency is
🔵 (A) 25 Hz
🟢 (B) 50 Hz
🟠 (C) 100 Hz
🔴 (D) 200 Hz
Answer: (B) 50 Hz
Year: 2015 | Paper 1
Question 18: The rms value of current for i = 5 sin(100πt) is
🔵 (A) 5 A
🟢 (B) 5/√2 A
🟠 (C) 10 A
🔴 (D) 10/√2 A
Answer: (B) 5/√2 A
Year: 2023 | Paper 2
Question 19: In a series LCR circuit at resonance, the current is
🔵 (A) limited by XL
🟢 (B) limited by XC
🟠 (C) limited by R
🔴 (D) maximum possible
Answer: (C) limited by R
Year: 2023 | Paper 2
Question 20: In a transformer, the efficiency can be increased by reducing
🔵 (A) eddy current loss
🟢 (B) hysteresis loss
🟠 (C) copper loss
🔴 (D) all of these
Answer: (D) all of these
Year: 2022 | Paper 2
Question 21: In an AC circuit, the instantaneous emf is e = 325 sin(100πt). The maximum value of emf is
🔵 (A) 325 V
🟢 (B) 230 V
🟠 (C) 220 V
🔴 (D) 311 V
Answer: (A) 325 V
Year: 2022 | Paper 2
Question 22: A circuit contains pure resistance R and inductive reactance XL in series. The phase difference between current and voltage is
🔵 (A) 0°
🟢 (B) tan⁻¹(XL/R)
🟠 (C) tan⁻¹(R/XL)
🔴 (D) 90°
Answer: (B) tan⁻¹(XL/R)
Year: 2021 | Paper 2
Question 23: In a purely resistive circuit supplied with AC of peak voltage V0, the average power is
🔵 (A) V0^2 / 2R
🟢 (B) V0^2 / R
🟠 (C) V0^2 / 4R
🔴 (D) 0
Answer: (A) V0^2 / 2R
Year: 2021 | Paper 2
Question 24: In an AC circuit, the current is i = 2 sin(100πt + π/3). The phase angle is
🔵 (A) 0°
🟢 (B) 30°
🟠 (C) 60°
🔴 (D) 90°
Answer: (C) 60°
Year: 2020 | Paper 2
Question 25: In a series RLC circuit at resonance, voltage across L is 200 V and across R is 50 V. Voltage across C is
🔵 (A) 0 V
🟢 (B) 50 V
🟠 (C) 200 V
🔴 (D) 250 V
Answer: (C) 200 V
Year: 2020 | Paper 2
Question 26: The average value of AC over a half cycle is
🔵 (A) 0
🟢 (B) 2I0/π
🟠 (C) I0/√2
🔴 (D) I0
Answer: (B) 2I0/π
Year: 2019 | Paper 2
Question 27: A choke coil works on principle of
🔵 (A) capacitance
🟢 (B) inductance
🟠 (C) resistance
🔴 (D) resonance
Answer: (B) inductance
Year: 2019 | Paper 2
Question 28: In an AC circuit, power factor is 0.5. If V and I are rms values, the power consumed is
🔵 (A) VI
🟢 (B) 0.5 VI
🟠 (C) 2 VI
🔴 (D) zero
Answer: (B) 0.5 VI
Year: 2018 | Paper 2
Question 29: The current in a circuit is i = 3 sin(ωt − π/4). The current
🔵 (A) lags by 45°
🟢 (B) leads by 45°
🟠 (C) in phase
🔴 (D) opposite in phase
Answer: (A) lags by 45°
Year: 2018 | Paper 2
Question 30: A capacitor of 100 μF is connected to AC source 220 V, 50 Hz. The capacitive reactance is
🔵 (A) 31.8 Ω
🟢 (B) 63.6 Ω
🟠 (C) 100 Ω
🔴 (D) 318 Ω
Answer: (A) 31.8 Ω
Year: 2017 | Paper 2
Question 31: In an AC circuit, the power consumed is VI cosφ. If φ = 90°, then power is
🔵 (A) maximum
🟢 (B) zero
🟠 (C) minimum but not zero
🔴 (D) infinite
Answer: (B) zero
Year: 2017 | Paper 2
Question 32: In a transformer, the ratio of primary to secondary turns is 2:1. The ratio of voltages Vp:Vs is
🔵 (A) 1:2
🟢 (B) 2:1
🟠 (C) 1:1
🔴 (D) 4:1
Answer: (B) 2:1
Year: 2016 | Paper 2
Question 33: In an AC circuit with applied emf e = E0 sinωt, the rms value of emf is
🔵 (A) E0
🟢 (B) E0/√2
🟠 (C) 2E0/π
🔴 (D) zero
Answer: (B) E0/√2
Year: 2016 | Paper 2
Question 34: In an AC circuit, applied voltage is v = 220 sin(100πt). The angular frequency is
🔵 (A) 50 rad/s
🟢 (B) 100 rad/s
🟠 (C) 314 rad/s
🔴 (D) 628 rad/s
Answer: (C) 314 rad/s
Year: 2015 | Paper 2
————————————————————————————————————————————————————————————————————————————
PRACTICE SETS FROM THIS LESSON
🔹 NEET-Level (Q1–Q20)
Q1.
The peak value of a sinusoidal current is 5 A. Its RMS value is:
🔵 (A) 2.5 A
🟢 (B) 3.54 A
🟠 (C) 5 A
🔴 (D) 7.07 A
Answer: (B) 3.54 A
✏️ Irms = I0/√2 = 5/1.414 = 3.54 A
Q2.
If Vrms = 110 V, the peak voltage is:
🔵 (A) 110 V
🟢 (B) 155 V
🟠 (C) 220 V
🔴 (D) 77 V
Answer: (B) 155 V
✏️ V0 = √2 × 110 = 155 V
Q3.
In a resistor, the phase difference between V and I is:
🔵 (A) 90°
🟢 (B) 0°
🟠 (C) 45°
🔴 (D) 180°
Answer: (B) 0°
Q4.
For a pure inductor:
🔵 (A) Current leads by 90°
🟢 (B) Voltage leads by 90°
🟠 (C) Both in phase
🔴 (D) Power maximum
Answer: (B) Voltage leads by 90°
Q5.
For a pure capacitor:
🔵 (A) Current lags by 90°
🟢 (B) Voltage leads by 90°
🟠 (C) Current leads by 90°
🔴 (D) Both in phase
Answer: (C) Current leads by 90°
Q6.
The frequency of AC in India is:
🔵 (A) 100 Hz
🟢 (B) 25 Hz
🟠 (C) 50 Hz
🔴 (D) 60 Hz
Answer: (C) 50 Hz
Q7.
Angular frequency of 50 Hz AC is:
🔵 (A) 100 rad/s
🟢 (B) 314 rad/s
🟠 (C) 628 rad/s
🔴 (D) 157 rad/s
Answer: (B) 314 rad/s
✏️ ω = 2π f = 2×3.14×50 = 314 rad/s
Q8.
Power consumed in pure inductor = ?
🔵 (A) Vrms Irms
🟢 (B) Zero
🟠 (C) Maximum
🔴 (D) Infinite
Answer: (B) Zero
Q9.
Power factor in pure resistive circuit:
🔵 (A) 0
🟢 (B) 1
🟠 (C) 0.5
🔴 (D) 0.707
Answer: (B) 1
Q10.
If peak current is 10 A, Irms = ?
🔵 (A) 7.07 A
🟢 (B) 14.1 A
🟠 (C) 5 A
🔴 (D) 10 A
Answer: (A) 7.07 A
✏️ Irms = 10/√2 = 7.07 A
Q11.
The unit of reactance is:
🔵 (A) Henry
🟢 (B) Ohm
🟠 (C) Farad
🔴 (D) Weber
Answer: (B) Ohm
Q12.
Power in pure capacitor circuit = ?
🔵 (A) Maximum
🟢 (B) Zero
🟠 (C) Vrms × Irms
🔴 (D) Minimum
Answer: (B) Zero
Q13.
The effective value of alternating current is that DC which produces:
🔵 (A) Same heating effect
🟢 (B) Same voltage drop
🟠 (C) Same charge flow
🔴 (D) Same resistance
Answer: (A) Same heating effect
Q14.
In AC circuit with only R, average power = ?
🔵 (A) Irms² R
🟢 (B) 0
🟠 (C) Vrms² / XL
🔴 (D) None
Answer: (A) Irms² R
Q15.
At resonance, impedance of LCR = ?
🔵 (A) XL
🟢 (B) XC
🟠 (C) R
🔴 (D) Zero
Answer: (C) R
Q16.
If R = 50 Ω, Irms = 2 A, Vrms = ?
🔵 (A) 50 V
🟢 (B) 100 V
🟠 (C) 150 V
🔴 (D) 25 V
Answer: (B) 100 V
✏️ Vrms = I × R = 2 × 50 = 100 V
Q17.
Power factor cosφ = ?
🔵 (A) R/Z
🟢 (B) XL/XC
🟠 (C) V/I
🔴 (D) Z/R
Answer: (A) R/Z
Q18.
Average power in LCR = ?
🔵 (A) Vrms Irms cosφ
🟢 (B) Vrms Irms
🟠 (C) 0
🔴 (D) I0² R
Answer: (A) Vrms Irms cosφ
Q19.
Which element stores energy in magnetic field?
🔵 (A) Resistor
🟢 (B) Capacitor
🟠 (C) Inductor
🔴 (D) Battery
Answer: (C) Inductor
Q20.
Which element stores energy in electric field?
🔵 (A) Resistor
🟢 (B) Capacitor
🟠 (C) Inductor
🔴 (D) None
Answer: (B) Capacitor
🔹 JEE Main-Level (Q21–Q40)
Q21.
A 0.2 H inductor connected to 60 Hz AC. XL = ?
🔵 (A) 75 Ω
🟢 (B) 25 Ω
🟠 (C) 10 Ω
🔴 (D) 5 Ω
Answer: (A) 75 Ω
✏️ XL = 2π f L = 2×3.14×60×0.2 ≈ 75 Ω
Q22.
A 100 μF capacitor at 50 Hz has XC = ?
🔵 (A) 31.8 Ω
🟢 (B) 318 Ω
🟠 (C) 3.18 Ω
🔴 (D) 0.318 Ω
Answer: (A) 31.8 Ω
Q23.
In an RLC circuit, Vrms = 220 V, R = 22 Ω, XL = 44 Ω, XC = 22 Ω. Find Irms.
🔵 (A) 5 A
🟢 (B) 7.07 A
🟠 (C) 10 A
🔴 (D) 3.3 A
Answer: (A) 5 A
✏️ Z = √(R²+(XL–XC)²) = √(22²+(22)²) = 44 Ω → Irms = 220/44 = 5 A
Q24.
Impedance formula for LCR:
🔵 (A) √(R²+(XL–XC)²)
🟢 (B) √(XL²+XC²)
🟠 (C) XL + XC
🔴 (D) None
Answer: (A) √(R²+(XL–XC)²)
Q25.
At resonance, current in RLC is:
🔵 (A) V/R
🟢 (B) V/Z
🟠 (C) Zero
🔴 (D) Infinite
Answer: (A) V/R
Q26.
If φ = 60°, power factor = ?
🔵 (A) 0.5
🟢 (B) 0.866
🟠 (C) 1
🔴 (D) 0
Answer: (A) 0.5
Q27.
In resonance, average power = ?
🔵 (A) Vrms²/R
🟢 (B) Vrms²/Z
🟠 (C) Zero
🔴 (D) None
Answer: (A) Vrms²/R
Q28.
In AC, instantaneous value = ?
🔵 (A) i = I0 cosωt
🟢 (B) i = I0 sinωt
🟠 (C) i = Irms sinωt
🔴 (D) i = Vrms/R
Answer: (B) i = I0 sinωt
Q29.
A 60 Ω resistor connected to 220 V, 50 Hz AC. Find power.
🔵 (A) 807 W
🟢 (B) 484 W
🟠 (C) 600 W
🔴 (D) 1000 W
Answer: (A) 807 W
✏️ P = Vrms²/R = (220²)/60 = 48400/60 ≈ 807 W
Q30.
In AC, average value over half cycle = 0.637 × peak. True or false?
🔵 (A) True
🟢 (B) False
🟠 (C) Depends on phase
🔴 (D) Only DC
Answer: (A) True
Q31.
Q-factor of resonance = ?
🔵 (A) ω0L/R
🟢 (B) R/ω0L
🟠 (C) √(L/C)
🔴 (D) None
Answer: (A) ω0L/R
Q32.
Bandwidth = ?
🔵 (A) ω0/Q
🟢 (B) ω0 × Q
🟠 (C) 1/√(LC)
🔴 (D) None
Answer: (A) ω0/Q
Q33.
In resonance, power factor = ?
🔵 (A) 1
🟢 (B) 0
🟠 (C) 0.5
🔴 (D) Infinite
Answer: (A) 1
Q34.
Transformer efficiency is high because:
🔵 (A) Works on AC
🟢 (B) No moving parts
🟠 (C) Core loss minimized
🔴 (D) All
Answer: (D) All
Q35.
Which law explains induced emf in AC generator?
🔵 (A) Faraday’s law
🟢 (B) Ohm’s law
🟠 (C) Ampere’s law
🔴 (D) Lenz’s law
Answer: (A) Faraday’s law
Q36.
Phase angle φ = tan⁻¹((XL–XC)/R). For R=0, φ=?
🔵 (A) 0°
🟢 (B) ±90°
🟠 (C) 180°
🔴 (D) 45°
Answer: (B) ±90°
Q37.
Average power in pure L or C = ?
🔵 (A) Vrms Irms
🟢 (B) 0
🟠 (C) Infinite
🔴 (D) None
Answer: (B) 0
Q38.
If Q-factor high → resonance curve is:
🔵 (A) Broad
🟢 (B) Narrow and sharp
🟠 (C) Flat
🔴 (D) None
Answer: (B) Narrow and sharp
Q39.
In LCR, maximum current flows at:
🔵 (A) Low frequency
🟢 (B) High frequency
🟠 (C) Resonant frequency
🔴 (D) DC only
Answer: (C) Resonant frequency
Q40.
Average power P = ?
🔵 (A) Vrms Irms cosφ
🟢 (B) Vrms Irms
🟠 (C) Irms² R only
🔴 (D) None
Answer: (A) Vrms Irms cosφ
🔹 JEE Advanced-Level (Q41–Q50)
Q41.
In LCR, R=20 Ω, L=0.1 H, C=100 μF, f=50 Hz. Find φ.
🔵 (A) 0°
🟢 (B) +90°
🟠 (C) –90°
🔴 (D) Small positive angle
Answer: (D) Small positive angle
✏️ XL = 2π f L = 31.4 Ω, XC = 1/(2π f C) = 31.8 Ω → XL–XC ≈ –0.4 Ω → tanφ = –0.4/20 ≈ –0.02 → φ ≈ small negative → but since |XL–XC| tiny, effectively “very small angle.”
Q42.
If R small, Q-factor becomes:
🔵 (A) Large
🟢 (B) Small
🟠 (C) Zero
🔴 (D) Infinite
Answer: (A) Large
Q43.
A parallel resonance circuit has:
🔵 (A) Minimum impedance
🟢 (B) Maximum impedance
🟠 (C) Zero impedance
🔴 (D) No resonance
Answer: (B) Maximum impedance
Q44.
Skin effect in AC refers to:
🔵 (A) Current concentrated at center
🟢 (B) Current concentrated near surface
🟠 (C) Resistance decreases
🔴 (D) Power increases
Answer: (B) Current concentrated near surface
Q45.
Power transferred in LCR at resonance:
🔵 (A) Maximum
🟢 (B) Minimum
🟠 (C) Zero
🔴 (D) None
Answer: (A) Maximum
Q46.
At resonance, reactive power = ?
🔵 (A) Maximum
🟢 (B) Zero
🟠 (C) Minimum
🔴 (D) Infinite
Answer: (B) Zero
Q47.
In high-Q circuit, bandwidth is:
🔵 (A) Large
🟢 (B) Small
🟠 (C) Infinite
🔴 (D) None
Answer: (B) Small
Q48.
In LC oscillations, energy oscillates at frequency:
🔵 (A) f = 1/(2π√(LC))
🟢 (B) f = √(LC)
🟠 (C) f = 1/(LC)
🔴 (D) f = π√(LC)
Answer: (A) 1/(2π√(LC))
Q49.
For φ=0°, average power is:
🔵 (A) Vrms Irms
🟢 (B) Zero
🟠 (C) Infinite
🔴 (D) Irms² R
Answer: (A) Vrms Irms
Q50.
In series LCR, bandwidth Δf = ?
🔵 (A) fr/Q
🟢 (B) fr × Q
🟠 (C) √(L/C)
🔴 (D) None
Answer: (A) fr/Q
————————————————————————————————————————————————————————————————————————————
MIND MAP
————————————————————————————————————————————————————————————————————————————
