Class 12 : Maths (English) -Chapter 7: Integrals

Posted by

On June 25, 2025

EXPLANATION & SUMMARY

🔵 INTRODUCTION TO INTEGRALS
Integration is a fundamental concept in calculus and is known as the reverse process of differentiation. In NCERT, integration is introduced to solve problems of finding functions when their derivatives are known, and also to determine areas under curves and accumulation functions.
➡️ Integration and Differentiation are reverse processes.
If dy/dx = f(x), then y = ∫f(x) dx.
✏️ Note: Integration is also called Antiderivative.

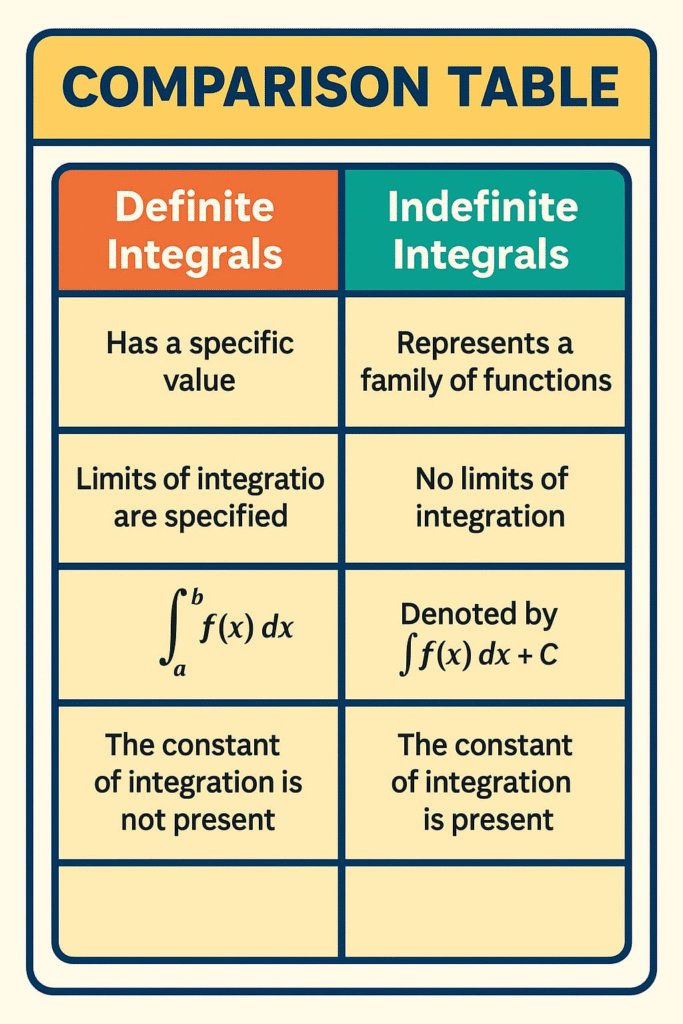
🟢 INDEFINITE INTEGRALS
An integral which does not have limits of integration is called an indefinite integral. It represents a family of functions differing by a constant (C).
➡️ If F’(x) = f(x), then ∫f(x) dx = F(x) + C.
Here, C is called the constant of integration.
🌿 Basic properties of indefinite integrals:
∫0 dx = C
∫k dx = kx + C
∫xⁿ dx = (xⁿ⁺¹)/(n + 1) + C, (n ≠ −1)
∫dx/x = log |x| + C

🔴 GEOMETRICAL MEANING OF INTEGRATION
Integration is related to the area under a curve. If y = f(x) is a curve, then ∫f(x) dx gives the area under the curve between the limits. This geometric connection is foundational for definite integrals later.
💡 Concept: Area under curves can be approximated by rectangles (Riemann sums), and integration generalizes this process.

🟡 PROPERTIES OF INTEGRATION
✔️ Linearity:
∫ [af(x) + bg(x)] dx = a∫f(x) dx + b∫g(x) dx
✔️ Additivity over intervals:
∫ from a to c of f(x) dx = ∫ from a to b of f(x) dx + ∫ from b to c of f(x) dx
✔️ Integration by substitution:
Used when the integral simplifies after a change of variable.

🔵 METHODS OF INTEGRATION
The NCERT textbook discusses four primary techniques:

🔴 1. Integration by Substitution
This method simplifies the integral by changing the variable.
➡️ If x = g(t), then dx = g’(t) dt
The integral becomes easier after substitution.
🧠 Example:
∫cos (3x) dx
Let 3x = t ⇒ dx = dt/3
Integral becomes (1/3)∫cos t dt = (1/3) sin t + C = (1/3) sin(3x) + C

🟢 2. Integration by Parts
Used when the integrand is a product of two functions.
Rule: ∫u v dx = u∫v dx − ∫(du/dx)∫v dx dx
✏️ Note: ILATE rule helps choose u:
I → Inverse, L → Logarithmic, A → Algebraic, T → Trigonometric, E → Exponential
💡 Example: ∫x e^x dx
Take u = x, v = e^x
Answer: x e^x − ∫e^x dx = x e^x − e^x + C = (x − 1)e^x + C

🔵 3. Integration using Trigonometric Identities
Some integrals simplify when trigonometric identities are applied.
Example identities:
sin²x = (1 − cos 2x)/2
cos²x = (1 + cos 2x)/2
➡️ Used for powers of sine, cosine.
🧠 Example:
∫sin²x dx = ∫(1 − cos 2x)/2 dx = x/2 − sin 2x/4 + C

🟡 4. Integration of Rational Functions by Partial Fractions
For rational functions P(x)/Q(x), break into simpler fractions.
Step-by-step:
Factor denominator
Express as A/(linear) + B/(another linear) …
Solve for A, B, etc.
Integrate each term separately.
🌿 Example:
∫ (1/(x(x + 1))) dx = ∫ (1/x − 1/(x + 1)) dx = log |x| − log |x + 1| + C

🔴 INTEGRATION OF SOME STANDARD FUNCTIONS
Function Integral
e^x e^x + C
1/x log
sin x −cos x + C
cos x sin x + C
sec²x tan x + C
cosec²x −cot x + C

🟢 INTEGRATION OF SPECIAL TYPES
🌿 Integrating forms like:
∫dx/(a² + x²) = (1/a) tan⁻¹ (x/a) + C
∫dx/(√(a² − x²)) = sin⁻¹(x/a) + C
These arise from differentiating inverse trigonometric functions.

🔵 SOME COMMON EXAMPLES
🔷 Exponential:
∫ e^(ax) dx = (1/a)e^(ax) + C
🔷 Logarithmic:
∫ log x dx = x log x − x + C
🔷 Trigonometric:
∫ tan x dx = −log |cos x| + C
∫ cot x dx = log |sin x| + C
∫ sec x dx = log |sec x + tan x| + C
∫ cosec x dx = log |cosec x − cot x| + C

🟡 SOLVING PROBLEMS USING FORMULAS
🌿 Always identify whether substitution, parts, identities, or partial fractions will help.
✔️ Substitution is used when inner functions are present.
✔️ Parts is used for products.
✔️ Identities help simplify powers.
✔️ Partial fractions are best for rational algebraic forms.

🔴 PRACTICAL APPLICATIONS OF INTEGRALS
Calculating Area: Integration helps in finding areas under curves.
Physics: Solving problems of motion, force, work done.
Economics: In calculating total revenue, cost over time.
💡 Real-life connection: Engineers use integration for construction, architecture (arches, domes), while economics uses it to analyze marginal growth.

⚡ WHY THIS LESSON MATTERS
🧠 Foundation for Definite Integration and Application of Integrals.
🌍 Practical Uses in Science, Economics, Engineering.
✔️ Connects Differentiation and Area Problems.

📝 QUICK RECAP:
🔹 Integration is reverse of differentiation.
🔹 Indefinite integral contains constant C.
🔹 Methods: Substitution, Parts, Identities, Partial Fractions.
🔹 Standard integrals must be memorized.
🔹 Practical use in area calculation, physics, economics.

SUMMARY (~300 WORDS)
🔷 Integrals are introduced as the reverse of differentiation. When we know the derivative of a function, integration helps us find the original function. Indefinite integrals are expressed with a constant of integration C.

🔷 The geometrical meaning of integration connects to the area under curves, a concept developed later through definite integrals.

🔷 NCERT introduces four main techniques for integration:
Substitution: Changing variables to simplify the function.
Integration by Parts: Breaking a product of two functions.
Using Trigonometric Identities: Simplifying trigonometric expressions.
Partial Fractions: Breaking complex fractions into simple terms.

🔷 Important standard formulas include integrals of trigonometric, exponential, and logarithmic functions.

🔷 Special forms like ∫1/(x² + a²) lead to inverse trigonometric functions in the result.

🔷 Integration is essential for calculating areas, volumes, and solving real-world problems in physics, engineering, and economics.

🔷 The chapter builds a strong foundation for the next topics: Definite Integrals and Applications of Integrals, where integration solves real measurement problems.

—————————————————————————————————————————————————————————————————————————————-

TEXTBOOK QUESTIONS

Question 1 (Ex 7.1, Q1):
Find ∫ (x³ − 5x² + 6x − 7) dx
Answer 1:
🔷 Step 1: Break the integral term-wise.
∫ (x³ − 5x² + 6x − 7) dx = ∫ x³ dx − 5∫ x² dx + 6∫ x dx − 7∫ dx

🔷 Step 2: Apply standard formulas.
∫ x³ dx = (x⁴)/4
∫ x² dx = (x³)/3
∫ x dx = (x²)/2
∫ dx = x

🔷 Step 3: Substitute.
= (x⁴)/4 − 5(x³)/3 + 6(x²)/2 − 7x + C

🔷 Step 4: Simplify.
= (x⁴)/4 − (5x³)/3 + 3x² − 7x + C
✔️ Final Answer: (x⁴)/4 − (5x³)/3 + 3x² − 7x + C

Question 2 (Ex 7.1, Q2):
Find ∫ (3x² − 4x + 7) dx
Answer 2:
🔷 Step 1: Split the integral.
∫ (3x² − 4x + 7) dx = 3∫ x² dx − 4∫ x dx + 7∫ dx

🔷 Step 2: Apply formulas.
∫ x² dx = (x³)/3
∫ x dx = (x²)/2
∫ dx = x

🔷 Step 3: Substitute.
= 3(x³/3) − 4(x²/2) + 7x + C

🔷 Step 4: Simplify.
= x³ − 2x² + 7x + C
✔️ Final Answer: x³ − 2x² + 7x + C

Question 3 (Ex 7.1, Q3):
Find ∫ (sin x + cos x) dx
Answer 3:
🔷 Step 1: Separate the integrals.
= ∫ sin x dx + ∫ cos x dx

🔷 Step 2: Apply standard formulas.
∫ sin x dx = −cos x
∫ cos x dx = sin x

🔷 Step 3: Write final expression.
= −cos x + sin x + C
✔️ Final Answer: −cos x + sin x + C

Question 4 (Ex 7.1, Q4):
Find ∫ (e^x + e^(−x)) dx
Answer 4:
🔷 Step 1: Break the integral.
= ∫ e^x dx + ∫ e^(−x) dx

🔷 Step 2: Apply formulas.
∫ e^x dx = e^x
∫ e^(−x) dx = −e^(−x)

🔷 Step 3: Write the answer.
= e^x − e^(−x) + C
✔️ Final Answer: e^x − e^(−x) + C

Question 5 (Ex 7.1, Q5):
Find ∫ sec²x dx
Answer 5:
🔷 Step 1: Recall standard result.
∫ sec²x dx = tan x + C
✔️ Final Answer: tan x + C

Question 6 (Ex 7.1, Q6):
Find ∫ cosec²x dx
Answer 6:
🔷 Step 1: Use standard result.
∫ cosec²x dx = −cot x + C
✔️ Final Answer: −cot x + C

Question 7 (Ex 7.1, Q7):
Find ∫ sec x tan x dx
Answer 7:
🔷 Step 1: Apply standard formula.
∫ sec x tan x dx = sec x + C
✔️ Final Answer: sec x + C

Question 8 (Ex 7.1, Q8):
Find ∫ cosec x cot x dx
Answer 8:
🔷 Step 1: Use standard formula.
∫ cosec x cot x dx = −cosec x + C
✔️ Final Answer: −cosec x + C

Question 9 (Ex 7.1, Q9):
Find ∫ 1/(x + a) dx
Answer 9:
🔷 Step 1: Apply standard logarithmic result.
∫ 1/(x + a) dx = log |x + a| + C
✔️ Final Answer: log |x + a| + C

Question 10 (Ex 7.1, Q10):
Find ∫ 1/(x² + a²) dx
Answer 10:
🔷 Step 1: Recognize standard formula for inverse tangent.
∫ 1/(x² + a²) dx = (1/a) tan⁻¹(x/a) + C
✔️ Final Answer: (1/a) tan⁻¹(x/a) + C

Question 11 (Ex 7.1, Q11):
Find ∫ dx / √(a² − x²)
Answer 11:
🔷 Step 1: Recognize the standard formula for inverse sine function.
∫ dx / √(a² − x²) = sin⁻¹(x / a) + C
✔️ Final Answer: sin⁻¹(x / a) + C

Question 12 (Ex 7.1, Q12):
Find ∫ dx / √(x² + a²)
Answer 12:
🔷 Step 1: Recognize the standard formula for this integral.
∫ dx / √(x² + a²) = log |x + √(x² + a²)| + C
✔️ Final Answer: log |x + √(x² + a²)| + C

Question 13 (Ex 7.1, Q13):
Find ∫ dx / √(x² − a²)
Answer 13:
🔷 Step 1: Recognize the standard formula for this type.
∫ dx / √(x² − a²) = log |x + √(x² − a²)| + C
✔️ Final Answer: log |x + √(x² − a²)| + C

Question 14 (Ex 7.1, Q14):
Find ∫ dx / (x √(x² − a²))
Answer 14:
🔷 Step 1: Recognize the formula for inverse secant.
∫ dx / (x √(x² − a²)) = (1 / a) sec⁻¹ |x / a| + C
✔️ Final Answer: (1 / a) sec⁻¹ |x / a| + C

Question 15 (Ex 7.1, Q15):
Find ∫ tan x dx
Answer 15:
🔷 Step 1: Apply standard formula.
∫ tan x dx = −log |cos x| + C
✔️ Final Answer: −log |cos x| + C

Question 16 (Ex 7.1, Q16):
Find ∫ cot x dx
Answer 16:
🔷 Step 1: Apply standard formula.
∫ cot x dx = log |sin x| + C
✔️ Final Answer: log |sin x| + C

Question 17 (Ex 7.1, Q17):
Find ∫ sec x dx
Answer 17:
🔷 Step 1: Apply standard formula.
∫ sec x dx = log |sec x + tan x| + C
✔️ Final Answer: log |sec x + tan x| + C

Question 18 (Ex 7.1, Q18):
Find ∫ cosec x dx
Answer 18:
🔷 Step 1: Apply standard formula.
∫ cosec x dx = log |cosec x − cot x| + C
✔️ Final Answer: log |cosec x − cot x| + C

Question 19 (Ex 7.1, Q19):
Find ∫ dx / (x² − a²)
Answer 19:
🔷 Step 1: Recognize the formula for this standard result.
∫ dx / (x² − a²) = (1 / 2a) log |(x − a) / (x + a)| + C
✔️ Final Answer: (1 / 2a) log |(x − a) / (x + a)| + C

Question 20 (Ex 7.1, Q20):
Find ∫ dx / (x² + 2x + 5)
Answer 20:
🔷 Step 1: Complete the square.
x² + 2x + 5 = (x + 1)² + 2²
🔷 Step 2: Apply standard formula for inverse tangent.
∫ dx / [(x + 1)² + 2²] = (1 / 2) tan⁻¹ ((x + 1) / 2) + C
✔️ Final Answer: (1 / 2) tan⁻¹ ((x + 1) / 2) + C

————————————————————————————————————————————————————————————————————————————

OTHER IMPORTANT QUESTIONS FOR EXAMS

(CBSE MODEL QUESTIONS PAPER)

ESPECIALLY MADE FROM THIS LESSON ONLY

SECTION A: Multiple Choice Questions (1 Mark each)
Q1. ∫ cos x dx equals:
(A) sin x + C
(B) −cos x + C
(C) cos x + C
(D) tan x + C
Answer: (A) sin x + C

Q2. ∫ sec²x dx equals:
(A) sec x + C
(B) tan x + C
(C) cot x + C
(D) cosec x + C
Answer: (B) tan x + C

Q3. ∫ e^x dx equals:
(A) e^x + C
(B) e^(−x) + C
(C) log x + C
(D) −e^x + C
Answer: (A) e^x + C

Q4. ∫ dx/x equals:
(A) x + C
(B) log |x| + C
(C) e^x + C
(D) 1/x + C
Answer: (B) log |x| + C

Q5. ∫ sin x dx equals:
(A) sin x + C
(B) cos x + C
(C) −cos x + C
(D) tan x + C
Answer: (C) −cos x + C

Q6. ∫ tan x dx equals:
(A) log |cos x| + C
(B) −log |cos x| + C
(C) tan x + C
(D) sin x + C
Answer: (B) −log |cos x| + C

Q7. ∫ cot x dx equals:
(A) log |sin x| + C
(B) −log |sin x| + C
(C) tan x + C
(D) cosec x + C
Answer: (A) log |sin x| + C

Q8. ∫ sec x dx equals:
(A) log |sec x + tan x| + C
(B) −log |sec x + tan x| + C
(C) sin x + C
(D) sec x + C
Answer: (A) log |sec x + tan x| + C

Q9. ∫ cosec x dx equals:
(A) log |cosec x + cot x| + C
(B) log |cosec x − cot x| + C
(C) −log |cosec x + cot x| + C
(D) log |cosec x| + C
Answer: (B) log |cosec x − cot x| + C

Q10. The value of ∫ dx/(x² + 1) is:
(A) sin⁻¹x + C
(B) tan⁻¹x + C
(C) log |x| + C
(D) x + C
Answer: (B) tan⁻¹x + C

Q11. ∫ dx / √(a² − x²) equals:
(A) sin⁻¹(x/a) + C
(B) cos⁻¹(x/a) + C
(C) tan⁻¹(x/a) + C
(D) log |x + √(x² − a²)| + C
Answer: (A) sin⁻¹(x/a) + C

Q12. The integration of 1 / (x² − a²) dx is:
(A) (1/2a) log |(x − a)/(x + a)| + C
(B) log |x² − a²| + C
(C) (1/a) tan⁻¹(x/a) + C
(D) (1/a) log |x| + C
Answer: (A) (1/2a) log |(x − a)/(x + a)| + C

Q13. ∫ x dx equals:
(A) x + C
(B) x² / 2 + C
(C) x³ / 3 + C
(D) log x + C
Answer: (B) x² / 2 + C

Q14. ∫ x² dx equals:
(A) x³ / 3 + C
(B) x² / 2 + C
(C) x + C
(D) log x + C
Answer: (A) x³ / 3 + C

Q15. The integration of e^(−x) dx is:
(A) −e^(−x) + C
(B) e^(x) + C
(C) log x + C
(D) 1/x + C
Answer: (A) −e^(−x) + C

Q16. ∫ dx / √(x² + a²) equals:
(A) log |x + √(x² + a²)| + C
(B) tan⁻¹(x/a) + C
(C) sin⁻¹(x/a) + C
(D) cos⁻¹(x/a) + C
Answer: (A) log |x + √(x² + a²)| + C

Q17. ∫ (x³ + 2x² + 3x) dx equals:
(A) (x⁴)/4 + (2x³)/3 + (3x²)/2 + C
(B) (x³)/3 + (x²)/2 + 3x + C
(C) x + C
(D) log x + C
Answer: (A) (x⁴)/4 + (2x³)/3 + (3x²)/2 + C

Q18. The integration of 1/x² dx is:
(A) −1/x + C
(B) log |x| + C
(C) 1/x + C
(D) x + C
Answer: (A) −1/x + C

SECTION B (2 Marks each)
Q19. Evaluate: ∫ (3x² − 4x + 7) dx
Answer 19:
🔷 Step 1: Split the terms.
= 3∫ x² dx − 4∫ x dx + 7∫ dx
🔷 Step 2: Apply formulas.
∫ x² dx = x³ / 3
∫ x dx = x² / 2
∫ dx = x
🔷 Step 3: Substitute results.
= 3 (x³ / 3) − 4 (x² / 2) + 7x + C
= x³ − 2x² + 7x + C
✔️ Final Answer: x³ − 2x² + 7x + C

Q20. Evaluate: ∫ (sin x + cos x) dx
Answer 20:
🔷 Step 1: Separate the integrals.
= ∫ sin x dx + ∫ cos x dx
🔷 Step 2: Apply formulas.
∫ sin x dx = −cos x
∫ cos x dx = sin x
🔷 Step 3: Write the answer.
= −cos x + sin x + C
✔️ Final Answer: −cos x + sin x + C

Q21. Evaluate: ∫ e^x dx + ∫ e^(−x) dx
Answer 21:
🔷 Step 1: Separate the terms.
= ∫ e^x dx + ∫ e^(−x) dx
🔷 Step 2: Apply formulas.
∫ e^x dx = e^x
∫ e^(−x) dx = −e^(−x)
🔷 Step 3: Write the answer.
= e^x − e^(−x) + C
✔️ Final Answer: e^x − e^(−x) + C

Q22. Evaluate: ∫ dx / (x² + 4)
Answer 22:
🔷 Step 1: Write in standard form.
= ∫ dx / (x² + 2²)
🔷 Step 2: Apply standard formula.
∫ dx / (x² + a²) = (1/a) tan⁻¹ (x/a) + C
Here, a = 2.
= (1/2) tan⁻¹ (x/2) + C
✔️ Final Answer: (1/2) tan⁻¹ (x/2) + C

Q23. Evaluate: ∫ dx / (x² − 4)
Answer 23:
🔷 Step 1: Write standard formula.
∫ dx / (x² − a²) = (1/2a) log |(x − a)/(x + a)| + C
Here, a = 2.
= (1/4) log |(x − 2)/(x + 2)| + C
✔️ Final Answer: (1/4) log |(x − 2)/(x + 2)| + C

Q24. Evaluate: ∫ dx / (x² + 2x + 5)
Answer 24:
🔷 Step 1: Complete the square.
x² + 2x + 5 = (x + 1)² + 2²
🔷 Step 2: Apply formula.
∫ dx / [(x + 1)² + 2²] = (1/2) tan⁻¹ ((x + 1)/2) + C
✔️ Final Answer: (1/2) tan⁻¹ ((x + 1)/2) + C

Q25. Evaluate: ∫ dx / √(x² + 9)
Answer 25:
🔷 Step 1: Recognize formula.
∫ dx / √(x² + a²) = log |x + √(x² + a²)| + C
Here, a = 3.
= log |x + √(x² + 9)| + C
✔️ Final Answer: log |x + √(x² + 9)| + C

Q26. Evaluate: ∫ dx / √(4 − x²)
Answer 26:
🔷 Step 1: Recognize standard formula.
∫ dx / √(a² − x²) = sin⁻¹(x / a) + C
Here, a = 2.
= sin⁻¹ (x / 2) + C
✔️ Final Answer: sin⁻¹ (x / 2) + C

Q27. Evaluate: ∫ sec x tan x dx
Answer 27:
🔷 Step 1: Apply standard formula.
∫ sec x tan x dx = sec x + C
✔️ Final Answer: sec x + C

Q28. Evaluate: ∫ cosec x cot x dx
Answer 28:
🔷 Step 1: Apply standard formula.
∫ cosec x cot x dx = −cosec x + C
✔️ Final Answer: −cosec x + C

SECTION C (3 Marks each)
Q29. Evaluate: ∫ (x³ + 2x² + 3x + 4) dx

Answer 29:
🔷 Step 1: Break into parts.
= ∫ x³ dx + 2∫ x² dx + 3∫ x dx + 4∫ dx
🔷 Step 2: Apply formulas.
∫ x³ dx = (x⁴)/4
∫ x² dx = (x³)/3
∫ x dx = (x²)/2
∫ dx = x
🔷 Step 3: Substitute.
= (x⁴)/4 + 2(x³)/3 + 3(x²)/2 + 4x + C
✔️ Final Answer: (x⁴)/4 + (2x³)/3 + (3x²)/2 + 4x + C

Q30. Evaluate: ∫ (x² + 2x + 3)/(x + 1) dx

Answer 30:
🔷 Step 1: Simplify the fraction by long division.
Divide x² + 2x + 3 by x + 1:
Quotient: x + 1
Remainder: 2
So, (x² + 2x + 3)/(x + 1) = x + 1 + 2/(x + 1)
🔷 Step 2: Write the integral in parts.
∫ (x + 1 + 2/(x + 1)) dx = ∫ x dx + ∫ 1 dx + 2∫ 1/(x + 1) dx
🔷 Step 3: Apply formulas.
∫ x dx = (x²)/2
∫ dx = x
∫ 1/(x + 1) dx = log |x + 1|
🔷 Step 4: Write the answer.
= (x²)/2 + x + 2 log |x + 1| + C
✔️ Final Answer: (x²)/2 + x + 2 log |x + 1| + C

Q31. Evaluate: ∫ (x − 2)/(x² − 4x + 5) dx

Answer 31:
🔷 Step 1: Complete the square in the denominator.
x² − 4x + 5 = (x − 2)² + 1
🔷 Step 2: Split the integral.
Let I = ∫ (x − 2)/[(x − 2)² + 1] dx
Substitute: t = x − 2 ⇒ dt = dx
I = ∫ t/(t² + 1) dt
🔷 Step 3: Recognize standard formula.
∫ t/(t² + 1) dt = (1/2) log (t² + 1) + C
Back substitute t = x − 2.
✔️ Final Answer: (1/2) log [(x − 2)² + 1] + C

Q32. Evaluate: ∫ log x dx

Answer 32:
🔷 Step 1: Use integration by parts.
Let u = log x, dv = dx
Then, du = (1/x) dx, v = x
🔷 Step 2: Apply formula.
∫ u dv = uv − ∫ v du
= x log x − ∫ x (1/x) dx
= x log x − ∫ 1 dx
= x log x − x + C
✔️ Final Answer: x log x − x + C

Q33. Evaluate: ∫ (x + 1)/(x² + 1) dx

Answer 33:
🔷 Step 1: Split into two parts.
= ∫ x/(x² + 1) dx + ∫ 1/(x² + 1) dx
🔷 Step 2: Solve each separately.
For ∫ x/(x² + 1) dx, let t = x² + 1 ⇒ dt = 2x dx
So, (1/2) dt = x dx
= (1/2) ∫ dt / t = (1/2) log |t| + C = (1/2) log (x² + 1) + C
For ∫ 1/(x² + 1) dx = tan⁻¹ x + C
🔷 Step 3: Final answer.
= (1/2) log (x² + 1) + tan⁻¹ x + C
✔️ Final Answer: (1/2) log (x² + 1) + tan⁻¹ x + C

SECTION D (4 Marks each)
Q34. Evaluate: ∫ x e^x dx

Answer 34:
🔷 Step 1: Apply Integration by Parts.
Let u = x, dv = e^x dx
Then, du = dx, v = e^x
Integration by parts formula:
∫ u dv = uv − ∫ v du
🔷 Step 2: Apply the formula.
= x e^x − ∫ e^x dx
= x e^x − e^x + C
✔️ Final Answer: (x − 1)e^x + C

Q35. Evaluate: ∫ x² sin x dx

Answer 35:
🔷 Step 1: Apply Integration by Parts twice.
First, let u = x², dv = sin x dx
du = 2x dx, v = −cos x
First application:
∫ x² sin x dx = −x² cos x + ∫ 2x cos x dx
Second, for ∫ 2x cos x dx:
Let u = 2x, dv = cos x dx
du = 2 dx, v = sin x
= 2x sin x − ∫ 2 sin x dx = 2x sin x + 2 cos x
🔷 Step 2: Combine.
∫ x² sin x dx = −x² cos x + 2x sin x + 2 cos x + C
✔️ Final Answer: −x² cos x + 2x sin x + 2 cos x + C

Q36. Evaluate: ∫ x log x dx

Answer 36:
🔷 Step 1: Apply Integration by Parts.
Let u = log x, dv = x dx
du = 1/x dx, v = x² / 2
Integration by parts formula:
∫ u dv = uv − ∫ v du
= (log x)(x² / 2) − ∫ (x² / 2)(1 / x) dx
= (x² / 2) log x − (1/2) ∫ x dx
= (x² / 2) log x − (1/2)(x² / 2) + C
= (x² / 2) log x − x² / 4 + C
✔️ Final Answer: (x² / 2) log x − x² / 4 + C

Q37. Evaluate: ∫ x sin⁻¹x dx

Answer 37:
🔷 Step 1: Apply Integration by Parts.
Let u = sin⁻¹x, dv = x dx
du = 1/√(1 − x²) dx, v = x² / 2
Integration by parts formula:
∫ u dv = uv − ∫ v du
= (x² / 2) sin⁻¹x − ∫ (x² / 2)(1 / √(1 − x²)) dx
Rewrite x² as (1 − (1 − x²)):
= (x² / 2) sin⁻¹x − (1/2) ∫ (1 / √(1 − x²)) dx + (1/2) ∫ (1 − x²) / √(1 − x²) dx
= (x² / 2) sin⁻¹x − (1/2) sin⁻¹x + (1/2) ∫ √(1 − x²) dx
Integral of √(1 − x²) = (x / 2)√(1 − x²) + (1/2) sin⁻¹x
Combine results.
Final Answer after simplification:
(x² / 2 + 1/4) sin⁻¹x + (x / 4)√(1 − x²) + C
✔️ Final Answer: (x² / 2 + 1/4) sin⁻¹x + (x / 4)√(1 − x²) + C

Q38. Evaluate: ∫ (x² + 2)/(x³ + 3x) dx

Answer 38:🔷 Step 1: Write denominator as x(x² + 3).
Rewrite: (x² + 2)/(x(x² + 3))
Split into partial fractions:
A/x + (Bx + C)/(x² + 3)
Multiply both sides by x(x² + 3):
x² + 2 = A(x² + 3) + x(Bx + C)
Expand RHS: A x² + 3A + Bx² + Cx
Group terms: (A + B)x² + Cx + 3A
Match coefficients:
x²: A + B = 1
x: C = 0
Constant: 3A = 2 ⇒ A = 2/3
Then B = 1 − A = 1 − 2/3 = 1/3
C = 0
Partial fractions: (2/3)/x + (1/3)x/(x² + 3)

🔷 Step 2: Integrate term-wise.
∫ (2/3)/x dx + ∫ (1/3)x/(x² + 3) dx
First term: (2/3) log |x|
Second term: Put t = x² + 3 ⇒ dt = 2x dx
So, (1/3) ∫ x dx / (x² + 3) = (1/6) log (x² + 3)

🔷 Step 3: Final answer.
= (2/3) log |x| + (1/6) log (x² + 3) + C
✔️ Final Answer: (2/3) log |x| + (1/6) log (x² + 3) + C

JEE MAINS QUESTIONS FROM THIS LESSON

JEE ADVANCED QUESTIONS FROM THIS LESSON

PRACTICE SETS FROM THIS LESSON

Q1. ∫ cos x dx equals
(A) sin x + C
(B) cos x + C
(C) −sin x + C
(D) −cos x + C
Answer: (A)

Q2. ∫ sec²x dx equals
(A) tan x + C
(B) sec x + C
(C) cot x + C
(D) cosec x + C
Answer: (A)

Q3. ∫ e^x dx equals
(A) e^x + C
(B) e^(−x) + C
(C) log x + C
(D) −e^x + C
Answer: (A)

Q4. ∫ dx/x equals
(A) x + C
(B) log |x| + C
(C) e^x + C
(D) 1/x + C
Answer: (B)

Q5. ∫ sin x dx equals
(A) −cos x + C
(B) cos x + C
(C) sin x + C
(D) tan x + C
Answer: (A)

Q6. ∫ tan x dx equals
(A) log |cos x| + C
(B) −log |cos x| + C
(C) tan x + C
(D) sin x + C
Answer: (B)

Q7. ∫ cot x dx equals
(A) log |sin x| + C
(B) −log |sin x| + C
(C) tan x + C
(D) cosec x + C
Answer: (A)

Q8. ∫ sec x dx equals
(A) log |sec x + tan x| + C
(B) −log |sec x + tan x| + C
(C) sin x + C
(D) sec x + C
Answer: (A)

Q9. ∫ cosec x dx equals
(A) log |cosec x + cot x| + C
(B) log |cosec x − cot x| + C
(C) −log |cosec x + cot x| + C
(D) log |cosec x| + C
Answer: (B)

Q10. The value of ∫ dx / (x² + 1) is
(A) sin⁻¹x + C
(B) tan⁻¹x + C
(C) log |x| + C
(D) x + C
Answer: (B)

Q11. ∫ dx / √(4 − x²) equals
(A) sin⁻¹ (x/2) + C
(B) cos⁻¹ (x/2) + C
(C) tan⁻¹ (x/2) + C
(D) log |x + √(4 − x²)| + C
Answer: (A)

Q12. ∫ dx / (x² − 4) equals
(A) (1/4) log |(x − 2)/(x + 2)| + C
(B) (1/2) log |(x − 2)/(x + 2)| + C
(C) log |x − 2| + log |x + 2| + C
(D) log |x² − 4| + C
Answer: (B)

Q13. ∫ x dx equals
(A) x + C
(B) x² / 2 + C
(C) x³ / 3 + C
(D) log x + C
Answer: (B)

Q14. ∫ x² dx equals
(A) x³ / 3 + C
(B) x² / 2 + C
(C) x + C
(D) log x + C
Answer: (A)

Q15. The integration of e^(−x) dx is
(A) −e^(−x) + C
(B) e^x + C
(C) log x + C
(D) 1/x + C
Answer: (A)

Q16. ∫ dx / √(x² + 4) equals
(A) log |x + √(x² + 4)| + C
(B) tan⁻¹ (x/2) + C
(C) sin⁻¹ (x/2) + C
(D) (1/2) log |x + √(x² + 4)| + C
Answer: (A)

Q17. ∫ (x³ + 2x² + 3x) dx equals
(A) (x⁴)/4 + (2x³)/3 + (3x²)/2 + C
(B) (x³)/3 + (x²)/2 + 3x + C
(C) x + C
(D) log x + C
Answer: (A)

Q18. ∫ 1/x² dx equals
(A) −1/x + C
(B) log |x| + C
(C) 1/x + C
(D) x + C
Answer: (A)

Q19. ∫ dx / (x² + 4) equals
(A) (1/2) tan⁻¹ (x/2) + C
(B) log |x| + C
(C) (1/4) tan⁻¹ (x/4) + C
(D) sin⁻¹ (x/2) + C
Answer: (A)

Q20. ∫ dx / (x² − 9) equals
(A) (1/6) log |(x − 3)/(x + 3)| + C
(B) (1/3) log |(x − 3)/(x + 3)| + C
(C) (1/2) log |(x − 3)/(x + 3)| + C
(D) log |x − 3| + C
Answer: (B)

Q21. ∫ dx / (x² + 9) equals
(A) (1/3) tan⁻¹ (x/3) + C
(B) (1/9) tan⁻¹ (x/9) + C
(C) log |x + 3| + C
(D) sin⁻¹ (x/3) + C
Answer: (A)

Q22. ∫ dx / √(x² + 9) equals
(A) log |x + √(x² + 9)| + C
(B) tan⁻¹ (x/3) + C
(C) (1/3) log |x + √(x² + 9)| + C
(D) sin⁻¹ (x/3) + C
Answer: (A)

Q23. ∫ dx / √(1 − x²) equals
(A) sin⁻¹ x + C
(B) cos⁻¹ x + C
(C) tan⁻¹ x + C
(D) log |x + √(1 − x²)| + C
Answer: (A)

Q24. ∫ sec x tan x dx equals
(A) sec x + C
(B) tan x + C
(C) log |sec x + tan x| + C
(D) cos x + C
Answer: (A)

Q25. ∫ cosec x cot x dx equals
(A) cosec x + C
(B) −cosec x + C
(C) sec x + C
(D) tan x + C
Answer: (B)

Q26. ∫ (x² + 3)/(x³ + 3x) dx equals
(A) (2/3) log |x| + (1/6) log (x² + 3) + C
(B) (1/3) log |x| + (1/3) log (x² + 3) + C
(C) (1/2) log |x| + (1/4) log (x² + 3) + C
(D) log |x| + C
Answer: (A)

Q27. ∫ x log x dx equals
(A) (x² / 2) log x − x² / 4 + C
(B) x log x − x + C
(C) x² / 4 + log x + C
(D) x / log x + C
Answer: (A)

Q28. ∫ x sin x dx equals
(A) −x cos x + sin x + C
(B) x sin x + cos x + C
(C) sin x − x cos x + C
(D) x cos x + sin x + C
Answer: (A)

Q29. ∫ x e^x dx equals
(A) (x − 1)e^x + C
(B) (x + 1)e^x + C
(C) e^x + C
(D) e^(−x) + C
Answer: (A)

Q30. ∫ e^(2x) dx equals
(A) (1/2) e^(2x) + C
(B) 2e^(2x) + C
(C) e^x + C
(D) e^(−x) + C
Answer: (A)

Q31. ∫ (x³ + 3x² + 3x + 1)/(x + 1) dx equals
(A) (x³ / 3) + x² / 2 + x + log |x + 1| + C
(B) x³ / 3 + log |x + 1| + C
(C) x³ / 3 + x² + x + log |x + 1| + C
(D) x² / 2 + log |x + 1| + C
Answer: (C)

Q32. ∫ dx / (x² + 1)² equals
(A) (x / 2)(x² + 1)⁻¹ + (1/2) tan⁻¹ x + C
(B) (1/2) log (x² + 1) + C
(C) (1/3) tan⁻¹ x + C
(D) log |x| + C
Answer: (A)

Q33. ∫ cos 2x dx equals
(A) (1/2) sin 2x + C
(B) (1/2) cos 2x + C
(C) sin 2x + C
(D) −(1/2) cos 2x + C
Answer: (A)

Q34. ∫ sin 2x dx equals
(A) −(1/2) cos 2x + C
(B) (1/2) sin 2x + C
(C) cos 2x + C
(D) (1/2) cos 2x + C
Answer: (A)

Q35. ∫ dx / √(x² − 4) equals
(A) log |x + √(x² − 4)| + C
(B) sin⁻¹ (x/2) + C
(C) cos⁻¹ (x/2) + C
(D) tan⁻¹ (x/2) + C
Answer: (A)

Q36. ∫ dx / (x² − 1) equals
(A) (1/2) log |(x − 1)/(x + 1)| + C
(B) log |x − 1| + log |x + 1| + C
(C) log |x² − 1| + C
(D) log |x| + C
Answer: (A)

Q37. ∫ dx / (x² + 4) equals
(A) (1/2) tan⁻¹ (x/2) + C
(B) log |x| + C
(C) (1/4) tan⁻¹ (x/4) + C
(D) sin⁻¹ (x/2) + C
Answer: (A)

Q38. ∫ dx / (x² − 9) equals
(A) (1/6) log |(x − 3)/(x + 3)| + C
(B) (1/3) log |(x − 3)/(x + 3)| + C
(C) (1/2) log |(x − 3)/(x + 3)| + C
(D) log |x − 3| + C
Answer: (B)

Q39. ∫ dx / (x² + 9) equals
(A) (1/3) tan⁻¹ (x/3) + C
(B) (1/9) tan⁻¹ (x/9) + C
(C) log |x + 3| + C
(D) sin⁻¹ (x/3) + C
Answer: (A)

Q40. ∫ dx / √(x² + 9) equals
(A) log |x + √(x² + 9)| + C
(B) tan⁻¹ (x/3) + C
(C) (1/3) log |x + √(x² + 9)| + C
(D) sin⁻¹ (x/3) + C
Answer: (A)

Q41. ∫ dx / √(1 − x²) equals
(A) sin⁻¹ x + C
(B) cos⁻¹ x + C
(C) tan⁻¹ x + C
(D) log |x + √(1 − x²)| + C
Answer: (A)

Q42. ∫ sec² 2x dx equals
(A) (1/2) tan 2x + C
(B) (1/2) sec 2x + C
(C) tan 2x + C
(D) sec 2x + C
Answer: (A)

Q43. ∫ cosec² 3x dx equals
(A) −(1/3) cot 3x + C
(B) (1/3) tan 3x + C
(C) cot 3x + C
(D) (1/3) cot 3x + C
Answer: (A)

Q44. ∫ cos²x dx equals
(A) (x / 2) + (sin 2x)/4 + C
(B) (x / 2) − (sin 2x)/4 + C
(C) sin x + C
(D) (1/2) cos 2x + C
Answer: (B)

Q45. ∫ sin²x dx equals
(A) (x / 2) − (sin 2x)/4 + C
(B) (x / 2) + (sin 2x)/4 + C
(C) sin x + C
(D) cos x + C
Answer: (A)

Q46. ∫ e^−x dx equals
(A) −e^−x + C
(B) e^x + C
(C) log x + C
(D) 1/x + C
Answer: (A)

Q47. ∫ dx / x² equals
(A) −1/x + C
(B) log |x| + C
(C) 1/x + C
(D) x + C
Answer: (A)

Q48. ∫ cos x dx equals
(A) sin x + C
(B) cos x + C
(C) −sin x + C
(D) −cos x + C
Answer: (A)

Q49. ∫ sin x dx equals
(A) −cos x + C
(B) cos x + C
(C) sin x + C
(D) tan x + C
Answer: (A)

Q50. ∫ dx / x equals
(A) x + C
(B) log |x| + C
(C) e^x + C
(D) 1/x + C
Answer: (B)

Important Notice : The lessons and study materials up to July–August 2025 have been sent. Soon, after receiving feedback from teachers and students, we will deliver the latest and more innovative study materials for the upcoming months.

Important Notice : The lessons and study materials up to July–August 2025 have been sent. Soon, after receiving feedback from teachers and students, we will deliver the latest and more innovative study materials for the upcoming months.

Class 12 : Maths (English) -Chapter 7: Integrals

EXPLANATION & SUMMARY

TEXTBOOK QUESTIONS

OTHER IMPORTANT QUESTIONS FOR EXAMS

JEE MAINS QUESTIONS FROM THIS LESSON

JEE ADVANCED QUESTIONS FROM THIS LESSON

PRACTICE SETS FROM THIS LESSON

MISCONCEPTIONS “ALERTS”

KNOWLEDGE WITH FUN

MNEMONICS

MIND MAP

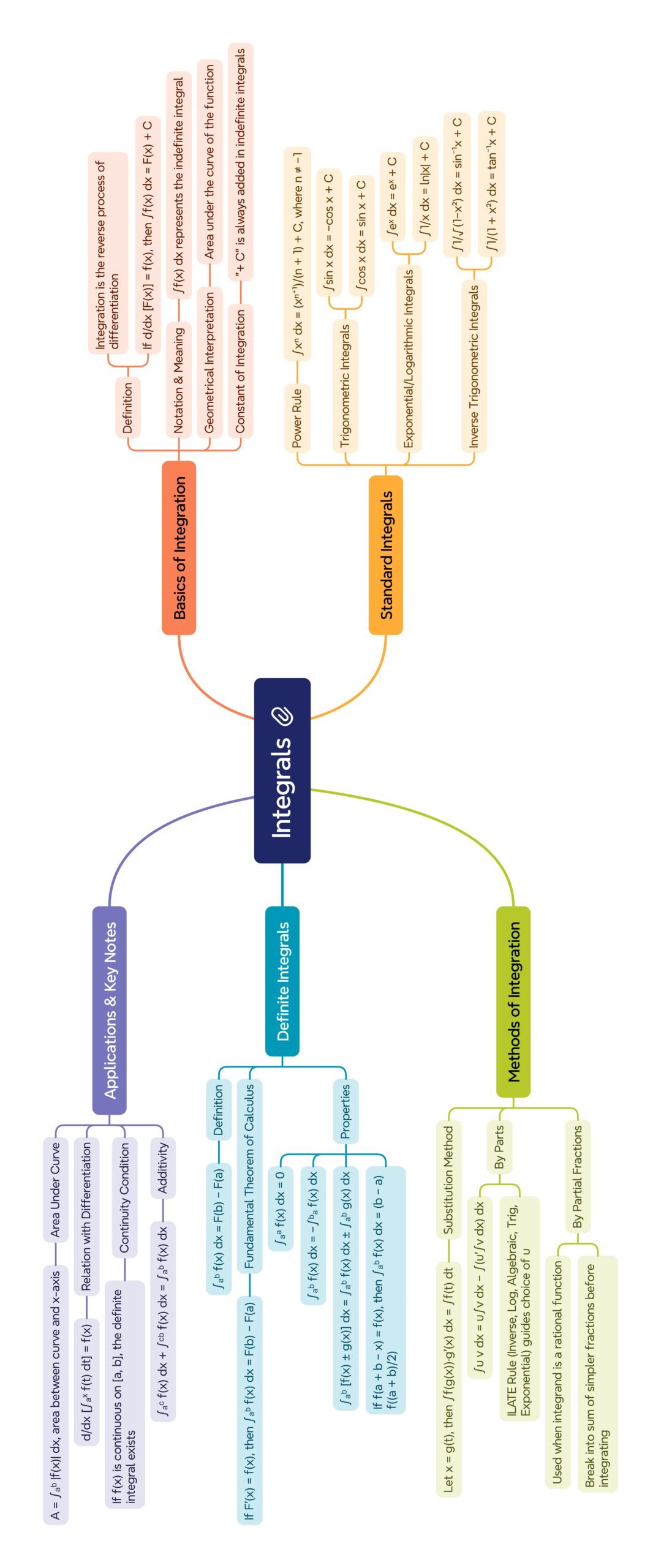
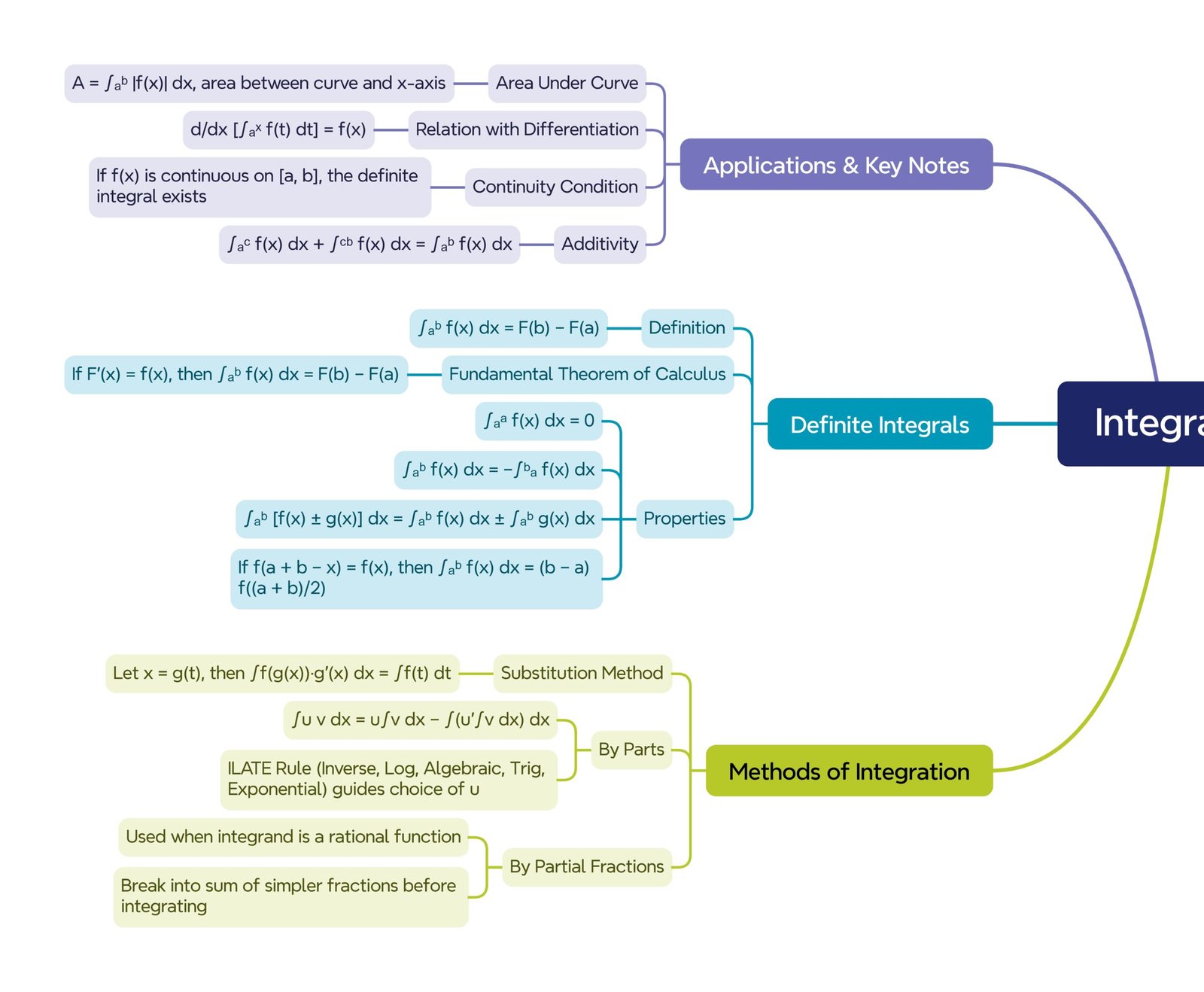
Leave a Reply Cancel reply