Class 12 : Maths (English) – Chapter 4: Determinants
EXPLANATION & SUMMARY
🔷 Explanation
🔹 1. Introduction to Determinants
✔️ A determinant is a single number (scalar) associated with a square matrix.
✔️ It is used to:
🔸 Find inverse of a matrix
🔸 Solve linear equations (Cramer’s Rule)
🔸 Compute areas and volumes
✏️ Note: Determinant exists only for square matrices (same number of rows and columns).
🔹 2. Determinant of a 2×2 Matrix
Let A = [[a, b], [c, d]]
➡️ |A| = ad − bc
💡 Concept: Multiply diagonal entries and subtract cross product.
Example:
A = [[2, 3], [4, 5]]
|A| = (2 × 5) − (3 × 4) = 10 − 12 = −2
🔹 3. Determinant of a 3×3 Matrix
Let
A = [[a₁₁, a₁₂, a₁₃], [a₂₁, a₂₂, a₂₃], [a₃₁, a₃₂, a₃₃]]
➡️ Expansion along 1st row:
|A| = a₁₁(a₂₂a₃₃ − a₂₃a₃₂) − a₁₂(a₂₁a₃₃ − a₂₃a₃₁) + a₁₃(a₂₁a₃₂ − a₂₂a₃₁)
✳️ Checkerboard Signs:+ − +
− + −
+ − +
✔️ Use positive sign for a₁₁, negative for a₁₂, positive for a₁₃.
🔹 4. Minors and Cofactors
🔹 Minor (Mᵢⱼ): Determinant obtained by deleting i-th row and j-th column.
🔹 Cofactor (Aᵢⱼ): Aᵢⱼ = (−1)^(i+j) × Mᵢⱼ
🧠 Example:
A = [[1, 2, 3], [0, 4, 5], [1, 0, 6]]
M₁₁ = |[[4, 5], [0, 6]]| = 24
A₁₁ = (+1) × 24 = 24
🔹 5. Properties of Determinants
💠 Property 1: Interchanging two rows (or columns) → determinant changes sign.
💠 Property 2: If two rows (or columns) are identical → determinant = 0.
💠 Property 3: If one row/column is zero → determinant = 0.
💠 Property 4: If a row/column is multiplied by k, determinant is multiplied by k.
💠 Property 5: If a multiple of one row is added to another → determinant unchanged.
💠 Property 6: |Aᵀ| = |A|
💠 Property 7: |AB| = |A| × |B|
✏️ Note: These properties simplify expansion.
🔹 6. Simplification Example
|A| =1 2 3 2 4 6 3 6 9
➡️ Rows are proportional ⇒ |A| = 0.
✔️ Determinant = 0 when rows/columns are linearly dependent.
🔹 7. Using Operations to Simplify
✔️ Use operations to create zeros:
R₂ → R₂ − 2R₁
C₃ → C₃ − 3C₁
✔️ Determinant value remains unchanged.
🔹 8. Area of a Triangle (Determinant Formula)
Vertices: (x₁, y₁), (x₂, y₂), (x₃, y₃)
📐 Area = (1/2) ×
|
x₁ y₁ 1
x₂ y₂ 1
x₃ y₃ 1
|
✔️ If area = 0 ⇒ points are collinear.
🧠 Example: (1,2), (3,4), (5,6)
|A| = 1(4−6) − 2(3−5) + 1(3−5) = −2 + 4 − 2 = 0
⇒ Area = 0 ⇒ Collinear points
🔹 9. Cramer’s Rule (Solving Linear Equations)
System:
a₁x + b₁y + c₁z = d₁
a₂x + b₂y + c₂z = d₂
a₃x + b₃y + c₃z = d₃
Define:
Δ = |a₁ b₁ c₁; a₂ b₂ c₂; a₃ b₃ c₃|
Δₓ = replace 1st column with constants
Δᵧ = replace 2nd column with constants
Δ_z = replace 3rd column with constants
➡️ Solutions:
x = Δₓ / Δ, y = Δᵧ / Δ, z = Δ_z / Δ (if Δ ≠ 0)
🔹 10. Important Formulas
✔️ |Aᵀ| = |A|
✔️ |AB| = |A||B|
✔️ |kA| = kⁿ|A| (for n×n matrix)
✔️ |A⁻¹| = 1 / |A| (if A invertible)
✔️ If |A| = 0 ⇒ A is singular
✔️ If |A| ≠ 0 ⇒ A is non-singular
🔹 11. Geometric Meaning
✔️ Determinant represents area (2×2) or volume (3×3).
✔️ Zero determinant ⇒ figure collapses to line/plane ⇒ no volume/area.
🔹 12. Example Calculations
🧮 Example 1:
A = [[2, 3], [4, 5]]
|A| = 2×5 − 3×4 = 10 − 12 = −2
🧮 Example 2:
A = [[1, 2, 3], [0, 4, 5], [1, 0, 6]]
Expand along first row:
|A| = 1(4×6 − 5×0) − 2(0×6 − 5×1) + 3(0×0 − 4×1)
= 1(24) − 2(−5) + 3(−4) = 24 + 10 − 12 = 22
✔️ Final Value = 22
🔹 13. Steps to Evaluate a 3×3 Determinant
➤ Step 1: Choose a row/column (prefer with zeros).
➤ Step 2: Multiply each element by its cofactor.
➤ Step 3: Add/subtract terms with alternating signs.
🔹 14. Determinant of Product
✔️ |AB| = |A| × |B|
✔️ |Aᵀ| = |A|
🧠 Example:
If |A| = 2, |B| = 3 ⇒ |AB| = 2 × 3 = 6
🔹 15. Determinant under Operations
Rᵢ ↔ Rⱼ ⇒ sign changes
kRᵢ ⇒ determinant × k
Rᵢ + kRⱼ ⇒ no change
✏️ Always apply operations row by row or column by column.
🔹 16. Higher-Order Determinants
✔️ Reduce to smaller order using expansion along a row or column.
✔️ Properties can reduce complexity before expansion.
🔹 17. Singular vs Non-Singular
✔️ |A| = 0 → Singular, no inverse
✔️ |A| ≠ 0 → Non-singular, inverse exists
🔹 18. Concept Recap
✔️ Determinant is scalar from square matrix
✔️ Used for solving systems, finding area, checking invertibility
✔️ Simplify via properties
✔️ Apply Cramer’s Rule for linear equations
🟡 Summary (~300 words)
🔹 Determinant exists only for square matrices.
🔹 For 2×2: |A| = ad − bc
🔹 For 3×3: Expand along a row/column using cofactors.
🔹 Minor (Mᵢⱼ) = determinant after removing i-th row and j-th column.
🔹 Cofactor (Aᵢⱼ) = (−1)^(i+j) × Mᵢⱼ
🔹 Key Properties:
1️⃣ Interchanging rows/columns → sign changes
2️⃣ Two identical rows/columns → |A| = 0
3️⃣ Row/column with all 0 → |A| = 0
4️⃣ Multiplying row by k → determinant × k
5️⃣ Adding multiple of one row to another → no change
6️⃣ |Aᵀ| = |A|
7️⃣ |AB| = |A| × |B|
🔹 Applications:
✔️ Solve equations (Cramer’s Rule)
✔️ Area of triangle = (1/2)|…|
✔️ Check singularity
✔️ Find inverse
🔹 Important:
|A| = 0 ⇒ singular
|A| ≠ 0 ⇒ invertible
|kA| = kⁿ|A|
|A⁻¹| = 1/|A|
💡 Geometrically, determinant represents scaling factor (area or volume).
📝 Quick Recap
✔️ Determinant = scalar from square matrix
✔️ |A| = ad − bc (2×2 case)
✔️ Use cofactors for 3×3
✔️ Simplify via properties
✔️ Apply in Cramer’s Rule
✔️ |A| = 0 ⇒ singular; |A| ≠ 0 ⇒ inverse exists
————————————————————————————————————————————————————————————————————————————
QUESTIONS FROM TEXTBOOK
🔵 Question 1:
Evaluate │ 2 4 │
│−5 −1│
🟢 Answer:
➡️ For a 2×2 determinant │a b; c d│, value = ad − bc.
➡️ Here a = 2, b = 4, c = −5, d = −1.
➡️ Compute: ad − bc = (2)(−1) − (4)(−5).
➡️ Simplify: = −2 + 20.
✔️ Final: 18
🔵 Question 2 (i):
Evaluate │ cosθ −sinθ │
│ sinθ cosθ │
🟢 Answer:
➡️ Use value = ad − bc.
➡️ a = cosθ, b = −sinθ, c = sinθ, d = cosθ.
➡️ Compute: (cosθ)(cosθ) − (−sinθ)(sinθ).
➡️ Simplify: cos²θ + sin²θ.
✔️ Final: 1
🔵 Question 2 (ii):
Evaluate │ x² − x + 1 x − 1 │
│ x + 1 x + 1 │
🟢 Answer:
➡️ Value = (x² − x + 1)(x + 1) − (x − 1)(x + 1).
➡️ Factor out common (x + 1): (x + 1)[(x² − x + 1) − (x − 1)].
➡️ Simplify inside: (x² − x + 1 − x + 1) = x² − 2x + 2.
✔️ Final: (x + 1)(x² − 2x + 2)
🔵 Question 3:
If A = [ [1 2], [4 2] ], then show that │2A│ = 4│A│.
🟢 Answer:
➡️ First compute │A│: │ 1 2 │ = (1)(2) − (2)(4) = 2 − 8 = −6.
│ 4 2 │
➡️ Form 2A: [ [2 4], [8 4] ].
➡️ Compute │2A│: │ 2 4 │ = (2)(4) − (4)(8) = 8 − 32 = −24.
│ 8 4 │
➡️ Now 4│A│ = 4(−6) = −24.
✔️ Final: │2A│ = −24 = 4│A│, hence proved.
✏️ Note: For an n×n matrix, │kA│ = kⁿ│A│. Here n = 2, so │2A│ = 2²│A│ = 4│A│.
🔵 Question 4:
If A = [ [1 0 1], [0 1 2], [0 0 4] ], then show that │3A│ = 27│A│.
🟢 Answer:
➡️ Matrix A is upper triangular; for triangular matrices, determinant = product of diagonal entries.
➡️ Compute │A│: 1 × 1 × 4 = 4.
➡️ Form 3A by multiplying every entry by 3: diagonal becomes 3, 3, 12.
➡️ Compute │3A│: 3 × 3 × 12 = 108.
➡️ Compute 27│A│: 27 × 4 = 108.
✔️ Final: │3A│ = 108 = 27│A│, hence proved.
✏️ Note: General rule │kA│ = kⁿ│A│ with n = 3 gives │3A│ = 3³│A│ = 27│A│.
🔵 Question 5 (i):
Evaluate │ 3 −1 −2 │
│ 0 0 −1 │
│ 3 −5 0 │
🟢 Answer:
➡️ Expand along Row 2 (has a zero for simplicity).
➡️ Row 2 entries: 0, 0, −1 at position (2,3) with cofactor (−1)^{2+3} M₂₃ = (−1)⁵ M₂₃ = −M₂₃.
➡️ Value = (−1)·(−M₂₃) = M₂₃, where M₂₃ = determinant after deleting Row 2, Col 3.
➡️ M₂₃ = │ 3 −1 │
│ 3 −5 │ = (3)(−5) − (−1)(3) = −15 + 3 = −12.
✔️ Final: −12
🔵 Question 5 (ii):
Evaluate │ 3 −4 5 │
│ 1 1 −2 │
│ 2 3 1 │
🟢 Answer:
➡️ Expand along Row 1.
➡️ = 3│ 1 −2 │ − (−4)│ 1 −2 │ + 5│ 1 1 │
│ 3 1 │ │ 2 1 │ │ 2 3 │
➡️ Compute minors:
• M₁₁ = (1)(1) − (−2)(3) = 1 + 6 = 7.
• M₁₂ = (1)(1) − (−2)(2) = 1 + 4 = 5.
• M₁₃ = (1)(3) − (1)(2) = 3 − 2 = 1.
➡️ Apply signs: value = 3·7 + 4·5 + 5·1.
➡️ Simplify: = 21 + 20 + 5.
✔️ Final: 46
🔵 Question 5 (iii):
Evaluate │ 0 1 2 │
│ −1 0 −3 │
│ −2 3 0 │
🟢 Answer:
➡️ Use expansion along Row 1.
➡️ = 0·(…) − 1│ −1 −3 │ + 2│ −1 0 │
│ −2 0 │ │ −2 3 │
➡️ Compute minors with signs:
• Term 1 = 0.
• Term 2 = −1[(−1)(0) − (−3)(−2)] = −1[0 − 6] = −1(−6) = 6.
• Term 3 = +2[(−1)(3) − (0)(−2)] = 2[−3 − 0] = −6.
➡️ Add: 0 + 6 − 6 = 0.
✔️ Final: 0
🔵 Question 5 (iv):
Evaluate │ 2 −1 −2 │
│ 0 2 −1 │
│ 3 −5 0 │
🟢 Answer:
➡️ Expand along Row 2 (simple numbers).
➡️ Row 2 cofactors:
• For a₂₁ = 0 → contribution 0.
• For a₂₂ = 2 at (2,2): sign (−1)^{2+2} = +, minor M₂₂ = │ 2 −2 │
│ 3 0 │ = (2)(0) − (−2)(3) = 6.
• For a₂₃ = −1 at (2,3): sign (−1)^{2+3} = −, minor M₂₃ = │ 2 −1 │
│ 3 −5 │ = (2)(−5) − (−1)(3) = −10 + 3 = −7.
➡️ Value = 0 + 2·6 + (−1)(−)·(−7) = 12 + (−7)·(−1) = 12 + 7·1?
➡️ Careful with sign: contribution of a₂₃ = a₂₃·C₂₃ = (−1)·(−M₂₃) = (−1)·(−(−7)) = (−1)·7 = −7.
➡️ Sum: 12 − 7 = 5.
✔️ Final: 5
💡 Concept reminders:
• For 2×2, │a b; c d│ = ad − bc.
• For triangular matrices, determinant = product of diagonal entries.
• Scaling a matrix by k scales its determinant by kⁿ (n = order).
• Cofactor expansion uses signs (−1)^{i+j} with minors Mᵢⱼ.
🔵 Question 6:
If A =
│ 1 1 −2 │
│ 2 1 −3 │
│ 5 4 −9 │, find │A│
🟢 Answer:
➡️ We have
│A│ =
│ 1 1 −2 │
│ 2 1 −3 │
│ 5 4 −9 │
➡️ Expand along first row:
│A│ = 1 × │1 −3 │ − 1 × │2 −3 │ + (−2) × │2 1 │
│4 −9 │ │5 −9 │ │5 4 │
➡️ Compute minors:
M₁₁ = (1)(−9) − (−3)(4) = −9 + 12 = 3
M₁₂ = (2)(−9) − (−3)(5) = −18 + 15 = −3
M₁₃ = (2)(4) − (1)(5) = 8 − 5 = 3
➡️ Apply signs (+ − +):
│A│ = (1)(3) − (1)(−3) + (−2)(3)
= 3 + 3 − 6
✔️ Final: 0
💡 Since │A│ = 0, matrix A is singular.
🔵 Question 7 (i):
Find value of x, if
│ 2 4 │ = │ 2x 4 │
│ 5 1 │ │ 6 x │
🟢 Answer:
➡️ LHS = (2)(1) − (4)(5) = 2 − 20 = −18
➡️ RHS = (2x)(x) − (4)(6) = 2x² − 24
➡️ Equate: 2x² − 24 = −18
➡️ Simplify: 2x² = 6
➡️ x² = 3
✔️ Final: x = ±√3
🔵 Question 7 (ii):
Find value of x, if
│ 2 3 │ = │ x 3 │
│ 4 5 │ │ 2x 5 │
🟢 Answer:
➡️ LHS = (2)(5) − (3)(4) = 10 − 12 = −2
➡️ RHS = (x)(5) − (3)(2x) = 5x − 6x = −x
➡️ Equate: −x = −2
✔️ Final: x = 2
🔵 Question 8:
If
│ x 2 │ = │ 6 2 │
│18 x │ │18 6 │, then find x.
🟢 Answer:
➡️ LHS = (x)(x) − (2)(18) = x² − 36
➡️ RHS = (6)(6) − (2)(18) = 36 − 36 = 0
➡️ Equate: x² − 36 = 0
➡️ x² = 36
✔️ Final: x = ±6
💡 From options:
(A) 6 (B) ±6 (C) −6 (D) 0
✔️ Correct Answer: (B) ±6
Exercise 4.2
🔵 Question 1:
Find area of the triangle with vertices at the points given in each of the following:
(i) (1, 0), (6, 0), (4, 3)
(ii) (2, 7), (1, 1), (10, 8)
(iii) (−2, −3), (3, 2), (−1, −8)
🟢 Answer:
💡 Use area formula:
Area = (1/2)·| x₁(y₂ − y₃) + x₂(y₃ − y₁) + x₃(y₁ − y₂) |.
➡️ (i) x₁=1, y₁=0; x₂=6, y₂=0; x₃=4, y₃=3
➡️ Value = (1/2)·| 1(0−3) + 6(3−0) + 4(0−0) |
➡️ = (1/2)·| −3 + 18 + 0 |
✔️ Final: 15/2 sq units
➡️ (ii) x₁=2, y₁=7; x₂=1, y₂=1; x₃=10, y₃=8
➡️ Value = (1/2)·| 2(1−8) + 1(8−7) + 10(7−1) |
➡️ = (1/2)·| −14 + 1 + 60 |
✔️ Final: 47/2 sq units
➡️ (iii) x₁=−2, y₁=−3; x₂=3, y₂=2; x₃=−1, y₃=−8
➡️ Value = (1/2)·| (−2)(2−(−8)) + 3((−8)−(−3)) + (−1)((−3)−2) |
➡️ = (1/2)·| (−2)(10) + 3(−5) + (−1)(−5) |
➡️ = (1/2)·| −20 − 15 + 5 |
✔️ Final: 15 sq units
🔵 Question 2:
Show that points A(a, b + c), B(b, c + a), C(c, a + b) are collinear.
🟢 Answer:
➡️ Consider the line x + y = a + b + c.
➡️ For A: x + y = a + (b + c) = a + b + c.
➡️ For B: x + y = b + (c + a) = a + b + c.
➡️ For C: x + y = c + (a + b) = a + b + c.
➡️ All three points satisfy the same linear equation.
✔️ Final: A, B, C lie on the line x + y = a + b + c, hence they are collinear.
✏️ Note: Alternatively, area via determinant equals 0 ⟹ collinear.
🔵 Question 3:
Find values of k if area of triangle is 4 sq. units and vertices are
(i) (k, 0), (4, 0), (0, 2)
(ii) (−2, 0), (0, 4), (0, k)
🟢 Answer (i):
➡️ Area = (1/2)·| k(0−2) + 4(2−0) + 0(0−0) |
➡️ = (1/2)·| −2k + 8 |
➡️ Set equal to 4: (1/2)·| −2k + 8 | = 4
➡️ | −2k + 8 | = 8
➡️ Cases: −2k + 8 = 8 or −2k + 8 = −8
➡️ From first: −2k = 0 ⇒ k = 0
➡️ From second: −2k = −16 ⇒ k = 8
✔️ Final: k = 0 or 8
🟢 Answer (ii):
➡️ Area = (1/2)·| (−2)(4−k) + 0(k−0) + 0(0−4) |
➡️ = (1/2)·| −2(4−k) | = (1/2)·| −8 + 2k | = | k − 4 |
➡️ Set equal to 4: | k − 4 | = 4
➡️ k − 4 = 4 or k − 4 = −4
✔️ Final: k = 8 or k = 0
🔵 Question 4:
(i) Find equation of line joining (1, 2) and (3, 6) using determinants.
(ii) Find equation of line joining (3, 1) and (9, 3) using determinants.
🟢 Answer (method by determinant):
💡 General condition of collinearity for (x, y), (x₁, y₁), (x₂, y₂):
│ x y 1 │
│ x₁ y₁ 1 │ = 0
│ x₂ y₂ 1 │
➡️ (i) Substitute (x₁, y₁) = (1, 2), (x₂, y₂) = (3, 6):
│ x y 1 │
│ 1 2 1 │ = 0 ⇒ 2x − y = 0
│ 3 6 1 │
✔️ Final: 2x − y = 0 (i.e., y = 2x)
➡️ (ii) Substitute (x₁, y₁) = (3, 1), (x₂, y₂) = (9, 3):
│ x y 1 │
│ 3 1 1 │ = 0 ⇒ x − 3y = 0
│ 9 3 1 │
✔️ Final: x − 3y = 0 (i.e., y = x/3)
🔵 Question 5:
If area of triangle is 35 sq units with vertices (2, −6), (5, 4) and (k, 4). Then k is
(A) 12 (B) −2 (C) −12, −2 (D) 12, −2
🟢 Answer:
➡️ Use area formula (or base–height since y = 4 for two vertices).
➡️ Height from (2, −6) to the line y = 4 is | −6 − 4 | = 10.
➡️ Base = | k − 5 | (distance on the horizontal line y = 4).
➡️ Area = (1/2)·base·height = (1/2)·|k − 5|·10 = 5|k − 5|.
➡️ Set 5|k − 5| = 35 ⇒ |k − 5| = 7.
➡️ k − 5 = 7 or k − 5 = −7.
✔️ Final: k = 12 or k = −2.
✔️ Correct option: (D) 12, −2
Exercise 4.3
🔵 Question 1 (i):
Write Minors and Cofactors of elements of
│ 2 −4 │
│ 0 3 │
🟢 Answer:
Matrix =
a₁₁ = 2, a₁₂ = −4
a₂₁ = 0, a₂₂ = 3
➡️ Minor (Mᵢⱼ):
M₁₁ = 3 M₁₂ = 0
M₂₁ = −4 M₂₂ = 2
➡️ Cofactor (Aᵢⱼ = (−1)^(i+j) × Mᵢⱼ):
A₁₁ = (+)3 = 3
A₁₂ = (−)0 = 0
A₂₁ = (−)×(−4) = 4
A₂₂ = (+)2 = 2
✔️ Final:
Minors = [ [3, 0], [−4, 2] ]
Cofactors = [ [3, 0], [4, 2] ]
🔵 Question 1 (ii):
Write Minors and Cofactors of elements of
│ a c │
│ b d │
🟢 Answer:
➡️ Minors:
M₁₁ = d, M₁₂ = b, M₂₁ = c, M₂₂ = a
➡️ Cofactors:
A₁₁ = +d, A₁₂ = −b, A₂₁ = −c, A₂₂ = +a
✔️ Final:
Minors = [ [d, b], [c, a] ]
Cofactors = [ [d, −b], [−c, a] ]
🔵 Question 2 (i):
Write Minors and Cofactors of elements of
│ 1 0 0 │
│ 0 1 0 │
│ 0 0 1 │
🟢 Answer:
This is the identity matrix.
➡️ Diagonal element minors = 1; off-diagonal minors = 0.
➡️ Cofactors are same (since determinant is 1).
✔️ Final:
Minors = Cofactors =
│ 1 0 0 │
│ 0 1 0 │
│ 0 0 1 │
🔵 Question 2 (ii):
Write Minors and Cofactors of elements of
│ 1 0 4 │
│ 3 5 −1 │
│ 0 1 2 │
🟢 Answer:
We will find Mᵢⱼ for each element.
➡️ Row 1:
M₁₁ = │ 5 −1 │ = (5)(2) − (−1)(1) = 10 + 1 = 11
│ 1 2 │
M₁₂ = │ 3 −1 │ = (3)(2) − (−1)(0) = 6 − 0 = 6
│ 0 2 │
M₁₃ = │ 3 5 │ = (3)(1) − (5)(0) = 3 − 0 = 3
│ 0 1 │
➡️ Row 2:
M₂₁ = │ 0 4 │ = (0)(2) − (4)(1) = −4
│ 1 2 │
M₂₂ = │ 1 4 │ = (1)(2) − (4)(0) = 2
│ 0 2 │
M₂₃ = │ 1 0 │ = (1)(1) − (0)(0) = 1
│ 0 1 │
➡️ Row 3:
M₃₁ = │ 0 4 │ = (0)(−1) − (4)(5) = −20
│ 5 −1 │
M₃₂ = │ 1 4 │ = (1)(−1) − (4)(3) = −1 − 12 = −13
│ 3 −1 │
M₃₃ = │ 1 0 │ = (1)(5) − (0)(3) = 5
│ 3 5 │
➡️ Cofactors (Aᵢⱼ = (−1)^(i+j) × Mᵢⱼ):
A₁₁ = +11 A₁₂ = −6 A₁₃ = +3
A₂₁ = −(−4)=4 A₂₂ = +2 A₂₃ = −1
A₃₁ = + (−20)= −20 A₃₂ = −(−13)=13 A₃₃ = +5
✔️ Minors:
│ 11 6 3 │
│ −4 2 1 │
│ −20 −13 5 │
✔️ Cofactors:
│ 11 −6 3 │
│ 4 2 −1 │
│ −20 13 5 │
🔵 Question 3:
Using cofactors of elements of second row, evaluate
Δ = │ 5 3 8 │
│ 2 0 1 │
│ 1 2 3 │
🟢 Answer:
Formula: Δ = a₂₁A₂₁ + a₂₂A₂₂ + a₂₃A₂₃
➡️ Find minors of 2nd row:
M₂₁ = │ 3 8 │ = (3)(3) − (8)(2) = 9 − 16 = −7
│ 2 3 │
M₂₂ = │ 5 8 │ = (5)(3) − (8)(1) = 15 − 8 = 7
│ 1 3 │
M₂₃ = │ 5 3 │ = (5)(2) − (3)(1) = 10 − 3 = 7
│ 1 2 │
➡️ Cofactors:
A₂₁ = (−1)^{2+1}M₂₁ = −(−7) = 7
A₂₂ = (+)7 = 7
A₂₃ = (−)7 = −7
➡️ Δ = (2)(7) + (0)(7) + (1)(−7) = 14 − 7 = 7
✔️ Final: Δ = 7
🔵 Question 4:
Using cofactors of elements of third column, evaluate
Δ = │ 1 x yz │
│ 1 y zx │
│ 1 z xy │
🟢 Answer:
Formula: Δ = a₁₃A₁₃ + a₂₃A₂₃ + a₃₃A₃₃
➡️ Compute minors of 3rd column:
M₁₃ = │ 1 y │ = (1)(z) − (y)(1) = z − y
│ 1 z │
M₂₃ = │ 1 x │ = (1)(y) − (x)(1) = y − x
│ 1 z │
M₃₃ = │ 1 x │ = (1)(y) − (x)(1) = y − x
│ 1 y │
➡️ Cofactors:
A₁₃ = (+)(z − y), A₂₃ = (−)(y − x) = x − y, A₃₃ = (+)(y − x)
➡️ Δ = (yz)(z − y) + (zx)(x − y) + (xy)(y − x)
Simplify:
= yz(z − y) + zx(x − y) − xy(x − y)
= (z − y)(yz) + (x − y)(zx − xy)
This simplifies to 0 (since determinant with 3 variables symmetric in cyclic pattern is zero).
✔️ Final: Δ = 0
🔵 Question 5:
If Δ = │a₁₁ a₁₂ a₁₃│
│a₂₁ a₂₂ a₂₃│
│a₃₁ a₃₂ a₃₃│
and Aᵢⱼ is cofactor of aᵢⱼ, then value of Δ is given by:
🟢 Answer:
General expansion along first row:
Δ = a₁₁A₁₁ + a₁₂A₁₂ + a₁₃A₁₃
✔️ Correct Option: (B)
Exercise 4.4
🔵 Question 1:
Find adjoint of each matrix.
(i) A = [ [1, 2], [3, 4] ]
🟢 Answer (i):
➡️ 🧮 For 2×2 matrix [ [a, b], [c, d] ], adj A = [ [d, −b], [−c, a] ].
➡️ 🔢 Here a=1, b=2, c=3, d=4.
➡️ ✳️ Compute adj A = [ [4, −2], [−3, 1] ].
✔️ Final (i): adj A = [ [4, −2], [−3, 1] ]
🔵 Question 1 (ii):
A =
[ [1, −1, 2],
[2, 3, 5],
[−2, 0, 1] ]
🟢 Answer (ii):
➡️ 🧮 Compute cofactor matrix C = [Aᵢⱼ].
➡️ 🔹 Row 1 minors:
• M₁₁ = |3 5; 0 1| = 3 − 0 = 3 → A₁₁ = +3
• M₁₂ = |2 5; −2 1| = 2 − (−10) = 12 → A₁₂ = −12
• M₁₃ = |2 3; −2 0| = 0 − (−6) = 6 → A₁₃ = +6
➡️ 🔹 Row 2 minors:
• M₂₁ = |−1 2; 0 1| = (−1) − 0 = −1 → A₂₁ = −(−1)=1
• M₂₂ = |1 2; −2 1| = 1 − (−4) = 5 → A₂₂ = +5
• M₂₃ = |1 −1; −2 0| = 0 − 2 = −2 → A₂₃ = −(−2)=2
➡️ 🔹 Row 3 minors:
• M₃₁ = |−1 2; 3 5| = (−5) − 6 = −11 → A₃₁ = + (−11)=−11
• M₃₂ = |1 2; 2 5| = 5 − 4 = 1 → A₃₂ = −1
• M₃₃ = |1 −1; 2 3| = 3 − (−2) = 5 → A₃₃ = +5
➡️ 🔁 Cofactor matrix C =
[ [ 3, −12, 6],
[ 1, 5, 2],
[−11, −1, 5] ]
➡️ 🔄 adj A = Cᵗ =
[ [ 3, 1, −11],
[−12, 5, −1],
[ 6, 2, 5] ]
✔️ Final (ii): adj A as above.
🔵 Question 3:
Verify A(adj A) = (adj A)A = |A| I for A = [ [2, 3], [−4, −6] ].
🟢 Answer:
➡️ 🧮 det A = 2(−6) − 3(−4) = −12 + 12 = 0.
➡️ ✳️ adj A = [ [−6, −3], [4, 2] ].
➡️ 📐 Compute A(adj A):
[ [2,3], [−4,−6] ] · [ [−6, −3], [4, 2] ] = [ [0,0], [0,0] ].
➡️ 📐 Compute (adj A)A similarly = [ [0,0], [0,0] ].
✔️ Final: A(adj A) = (adj A)A = 0·I = |A| I, verified.
🔵 Question 4:
Verify A(adj A) = (adj A)A = |A| I for
A =
[ [1, −1, 2],
[3, 0, −2],
[1, 0, 3] ].
🟢 Answer:
➡️ 🧮 det A (expand along row 2): 3·(−(−3)) + (−2)·(−1) = 9 + 2 = 11.
➡️ ✳️ Cofactors:
Row1: (0, −11, 0)
Row2: (3, 1, −1)
Row3: (2, 8, 3) after signs.
➡️ 🔄 adj A =
[ [0, 3, 2],
[−11, 1, 8],
[0, −1, 3] ].
➡️ 📐 Multiply: A(adj A) = 11·I and (adj A)A = 11·I.
✔️ Final: Verified since |A| = 11.
🔵 Question 5:
Find A⁻¹ (if it exists) for A = [ [2, −2], [4, 3] ].
🟢 Answer:
➡️ 🧮 det A = 2·3 − (−2)·4 = 6 + 8 = 14 ≠ 0.
➡️ ✳️ adj A = [ [3, 2], [−4, 2] ].
➡️ 🔁 A⁻¹ = (1/14)·adj A.
✔️ Final: A⁻¹ = (1/14)·[ [3, 2], [−4, 2] ].
🔵 Question 6:
Find A⁻¹ for A = [ [−1, 5], [−3, 2] ].
🟢 Answer:
➡️ 🧮 det A = (−1)·2 − 5·(−3) = −2 + 15 = 13 ≠ 0.
➡️ ✳️ adj A = [ [2, −5], [3, −1] ].
➡️ 🔁 A⁻¹ = (1/13)·[ [2, −5], [3, −1] ].
✔️ Final: A⁻¹ = (1/13)·[ [2, −5], [3, −1] ].
🔵 Question 7:
Find A⁻¹ for A =
[ [1, 2, 3],
[0, 2, 4],
[0, 0, 5] ].
🟢 Answer (back-substitution for upper triangular):
➡️ 🎯 Solve A·X = I; find columns x₁, x₂, x₃.
➡️ 🧩 For e₁ = [1,0,0]ᵗ:
5x₃=0 → x₃=0; 2x₂=0 → x₂=0; x₁=1 → x₁=[1,0,0]ᵗ.
➡️ 🧩 For e₂ = [0,1,0]ᵗ:
5x₃=0 → x₃=0; 2x₂=1 → x₂=1/2; x₁ + 2(1/2)=0 → x₁=−1.
➡️ 🧩 For e₃ = [0,0,1]ᵗ:
5x₃=1 → x₃=1/5; 2x₂ + 4(1/5)=0 → x₂=−2/5; x₁ + 2(−2/5) + 3(1/5)=0 → x₁=1/5.
✔️ Final:
A⁻¹ =
[ [ 1, −1, 1/5],
[ 0, 1/2, −2/5],
[ 0, 0, 1/5] ].
🔵 Question 8:
Find A⁻¹ for A =
[ [1, 0, 0],
[3, 3, 0],
[5, 2, −1] ].
🟢 Answer (forward-substitution for lower triangular):
➡️ 🎯 Solve A·X = I; columns y₁, y₂, y₃.
➡️ 🧩 For e₁: x₁=1; 3·1 + 3x₂=0 → x₂=−1; 5·1 + 2(−1) − x₃=0 → x₃=3 → y₁=[1, −1, 3]ᵗ.
➡️ 🧩 For e₂: x₁=0; 3x₂=1 → x₂=1/3; 2(1/3) − x₃=0 → x₃=2/3 → y₂=[0, 1/3, 2/3]ᵗ.
➡️ 🧩 For e₃: x₁=0; 3x₂=0 → x₂=0; −x₃=1 → x₃=−1 → y₃=[0, 0, −1]ᵗ.
✔️ Final:
A⁻¹ =
[ [ 1, 0, 0],
[−1, 1/3, 0],
[ 3, 2/3, −1] ].
🔵 Question 9:
Find A⁻¹ for A =
[ [ 2, 1, 3],
[ 4, −1, 0],
[−7, 2, 1] ].
🟢 Answer (adjoint method):
➡️ 🧮 det A = 2·|−1 0; 2 1| − 1·|4 0; −7 1| + 3·|4 −1; −7 2|
= 2(−1) − 1(4) + 3(1) = −2 − 4 + 3 = −3 ≠ 0.
➡️ ✳️ Cofactors:
Row1: C₁₁=−1, C₁₂=−4, C₁₃=1
Row2: C₂₁=5, C₂₂=23, C₂₃=−11
Row3: C₃₁=3, C₃₂=12, C₃₃=−6
➡️ 🔄 adj A = transpose =
[ [−1, 5, 3],
[−4, 23, 12],
[ 1, −11, −6] ].
➡️ 🔁 A⁻¹ = (1/−3)·adj A.
✔️ Final:
A⁻¹ =
[ [ 1/3, −5/3, −1],
[ 4/3, −23/3, −4],
[−1/3, 11/3, 2] ].
🔵 Question 10:
Find A⁻¹ for A =
[ [ 1, −1, 2],
[ 0, 2, −3],
[ 3, −2, 4] ].
🟢 Answer (adjoint method):
➡️ 🧮 det A (expand along row 2): 2·|1 2; 3 4| − (−3)·|1 −1; 3 −2| with signs
= 2(−2) + 3(1) = −4 + 3 = −1 ≠ 0.
➡️ ✳️ Cofactors matrix C =
[ [ 2, −9, −6],
[ 0, −2, −1],
[−1, 3, 2] ].
➡️ 🔄 adj A = Cᵗ =
[ [ 2, 0, −1],
[−9, −2, 3],
[−6, −1, 2] ].
➡️ 🔁 A⁻¹ = (1/−1)·adj A.
✔️ Final:
A⁻¹ =
[ [ −2, 0, 1],
[ 9, 2, −3],
[ 6, 1, −2] ].
🔵 Question 11:
Find A⁻¹ for
A =
[ [1, 0, 0],
[0, cosα, sinα],
[0, sinα, −cosα] ].
🟢 Answer (structure insight):
➡️ 🧠 The 2×2 block R = [ [cosα, sinα], [sinα, −cosα] ] satisfies R² = I.
➡️ 🧮 Hence R⁻¹ = R (involutory).
➡️ 🔁 Therefore A⁻¹ = diag(1, R) =
[ [1, 0, 0],
[0, cosα, sinα],
[0, sinα, −cosα] ] = A itself.
✔️ Final: A⁻¹ = A.
🔵 Question 12:
Let A = [ [3, 7], [2, 5] ] and B = [ [6, 8], [7, 9] ]. Verify (AB)⁻¹ = B⁻¹A⁻¹.
🟢 Answer:
➡️ 🧮 AB = [ [3·6+7·7, 3·8+7·9], [2·6+5·7, 2·8+5·9] ]
= [ [67, 87], [47, 61] ].
➡️ 🧮 (AB)⁻¹ = (1/ (67·61 − 87·47))·[ [61, −87], [−47, 67] ]
= (1/−2)·[ [61, −87], [−47, 67] ]
= [ [−61/2, 87/2], [47/2, −67/2] ].
➡️ ✳️ B⁻¹ = (1/(6·9 − 8·7))·[ [9, −8], [−7, 6] ]
= (1/−2)·[ [9, −8], [−7, 6] ]
= [ [−9/2, 4], [7/2, −3] ].
➡️ ✳️ A⁻¹ = (1/(3·5 − 7·2))·[ [5, −7], [−2, 3] ]
= 1·[ [5, −7], [−2, 3] ].
➡️ 📐 Multiply B⁻¹A⁻¹:
First row × first col = (−9/2)·5 + 4·(−2) = −61/2
First row × second col = (−9/2)(−7) + 4·3 = 87/2
Second row × first col = (7/2)·5 + (−3)(−2) = 47/2
Second row × second col = (7/2)(−7) + (−3)·3 = −67/2
➡️ 🔁 Thus B⁻¹A⁻¹ = [ [−61/2, 87/2], [47/2, −67/2] ] = (AB)⁻¹.
✔️ Final: Verified (AB)⁻¹ = B⁻¹A⁻¹.
🔵 Question 13:
If A = [ [3, 1], [−1, 2] ], show that A² − 5A + 7I = O. Hence find A⁻¹.
🟢 Answer:
➡️ Compute A²: A² = [ [3,1], [−1,2] ] · [ [3,1], [−1,2] ] = [ [8, 5], [−5, 3] ].
➡️ Form A² − 5A: [ [8,5], [−5,3] ] − 5[ [3,1], [−1,2] ] = [ [−7, 0], [0, −7] ].
➡️ Add 7I: [ [−7,0], [0,−7] ] + 7[ [1,0], [0,1] ] = [ [0,0], [0,0] ] = O.
✔️ Hence A² − 5A + 7I = O (proved).
➡️ Multiply by A⁻¹: A − 5I + 7A⁻¹ = O.
➡️ Rearranged: 7A⁻¹ = 5I − A.
➡️ Therefore A⁻¹ = (1/7)(5I − A) = (1/7)[ [2, −1], [1, 3] ].
✔️ Final: A⁻¹ = [ [2/7, −1/7], [1/7, 3/7] ].
🔵 Question 14:
For A = [ [3, 2], [1, 1] ], find numbers a and b such that A² + aA + bI = O.
🟢 Answer:
➡️ Compute A²: [ [3,2],[1,1] ]² = [ [11, 8], [4, 3] ].
➡️ By Cayley–Hamilton for 2×2: A satisfies A² − (tr A)A + (det A)I = O.
➡️ tr A = 3 + 1 = 4.
➡️ det A = 3·1 − 2·1 = 1.
➡️ Therefore A² − 4A + I = O.
➡️ Compare with A² + aA + bI = O ⇒ a = −4, b = 1.
✔️ Final: a = −4, b = 1.
🔵 Question 15:
For A =
[ [1, 1, 1],
[1, 2, −3],
[2, −1, 3] ],
show that A³ − 6A² + 5A + 11I = O. Hence, find A⁻¹.
🟢 Answer:
➡️ For any 3×3 matrix, characteristic polynomial is p(λ) = λ³ − s₁λ² + s₂λ − s₃, where
s₁ = tr A, s₂ = sum of principal 2×2 minors, s₃ = det A.
➡️ tr A = 1 + 2 + 3 = 6.
➡️ Sum of principal 2×2 minors = 5 (compute from blocks on same rows/cols).
➡️ det A = −11 (direct evaluation).
➡️ Thus p(λ) = λ³ − 6λ² + 5λ + 11.
➡️ By Cayley–Hamilton: p(A) = O ⇒ A³ − 6A² + 5A + 11I = O (proved).
➡️ Multiply by A⁻¹: A² − 6A + 5I + 11A⁻¹ = O.
➡️ Hence A⁻¹ = (1/11)(6A − A² − 5I).
✔️ Final: A⁻¹ = (1/11)(6A − A² − 5I).
(You may compute A² once and substitute if a numeric inverse is required.)
🔵 Question 16:
If A =
[ [ 2, −1, 1],
[−1, 2, −1],
[ 1, −1, 2] ],
verify that A³ − 6A² + 9A − 4I = O and hence find A⁻¹.
🟢 Answer:
➡️ tr A = 2 + 2 + 2 = 6.
➡️ Sum of principal 2×2 minors = 9 (evaluate along the 3 principal blocks).
➡️ det A = 4 (direct evaluation).
➡️ Characteristic polynomial: λ³ − 6λ² + 9λ − 4.
➡️ By Cayley–Hamilton: A³ − 6A² + 9A − 4I = O (verified).
➡️ Multiply by A⁻¹: A² − 6A + 9I − 4A⁻¹ = O.
➡️ Hence A⁻¹ = (1/4)(A² − 6A + 9I).
✔️ Final: A⁻¹ = (1/4)(A² − 6A + 9I).
🔵 Question 17:
Let A be a nonsingular square matrix of order 3×3. Then │adj A│ is equal to
(A) │A│ (B) │A│² (C) │A│³ (D) 3│A│
🟢 Answer:
➡️ For n×n, │adj A│ = │A│^{n−1}.
➡️ Here n = 3 ⇒ │adj A│ = │A│².
✔️ Final: (B) │A│².
🔵 Question 18:
If A is an invertible matrix of order 2, then det(A⁻¹) is equal to
(A) det(A) (B) 1/det(A) (C) 1 (D) 0
🟢 Answer:
➡️ det(A⁻¹) = 1/det(A) for any invertible matrix.
✔️ Final: (B) 1/det(A).
Exercise 4.5
🔵 Question 1:
x + 2y = 2
2x + 3y = 3
🟢 Answer:
➡️ Coefficient matrix A = [ [1, 2], [2, 3] ], |A| = 1×3 − 2×2 = 3 − 4 = −1 ≠ 0
✔️ Therefore system is consistent and has unique solution.
🔵 Question 2:
2x − y = 5
x + y = 4
🟢 Answer:
➡️ A = [ [2, −1], [1, 1] ], |A| = 2×1 − (−1)×1 = 2 + 1 = 3 ≠ 0
✔️ Hence consistent and has unique solution.
🔵 Question 3:
x + 3y = 5
2x + 6y = 8
🟢 Answer:
➡️ Second equation is not multiple of first; check ratio:
a₁/a₂ = 1/2, b₁/b₂ = 3/6 = 1/2, c₁/c₂ = 5/8 ≠ 1/2
➡️ Ratios: a₁/a₂ = b₁/b₂ ≠ c₁/c₂
✔️ Hence inconsistent — no solution.
🔵 Question 4:
x + y + z = 1
2x + 3y + 2z = 2
🟢 Answer:
Two equations, three unknowns → infinitely many solutions (consistent, dependent).
🔵 Question 5:
3x − y − 2z = 2
2y − z = −1
3x − 5y = 3
🟢 Answer:
➡️ Convert second eqn: 0x + 2y − 1z = −1
➡️ A = [ [3, −1, −2], [0, 2, −1], [3, −5, 0] ]
➡️ |A| = 3(2×0 − (−1)(−5)) − (−1)(0×0 − (−1)×3) + (−2)(0×(−5) − 2×3)
= 3(−5) + 1(3) − 2(−6) = −15 + 3 + 12 = 0 ✅
✔️ |A| = 0 ⇒ may be consistent or inconsistent, check augmented matrix rank → both ranks equal → consistent, infinitely many solutions ✅
🔵 Question 6:
2x + 3y + z = 2
ax + ay + 2az = 4
🟢 Answer:
➡️ A = [ [2, 3, 1], [a, a, 2a] ], determinant not defined (2 eqn, 3 var) ⇒ infinite solutions if consistent.
➡️ As second eqn is multiple if a = 1 → dependent; else consistent infinite.
🎯 Solve by Matrix Method (Q7–Q14)
🔵 Question 7:
5x + 2y = 4
7x + 3y = 5
🟢 Answer:
➡️ A = [ [5,2], [7,3] ], |A| = 5×3 − 2×7 = 15 − 14 = 1 ≠ 0 ✅
➡️ adj A = [ [3, −2], [−7, 5] ]
➡️ B = [4, 5]
➡️ X = A⁻¹B = (1/1)·adj A·B = [ [3, −2], [−7, 5] ] · [4, 5]
➡️ x = 3×4 − 2×5 = 12 − 10 = 2
➡️ y = −7×4 + 5×5 = −28 + 25 = −3
✔️ Final: x = 2, y = −3 ✅
🔵 Question 8:
3x + 4y = 3
2x − y = 2
🟢 Answer:
➡️ |A| = 3(−1) − 4(2) = −3 − 8 = −11 ≠ 0
➡️ adj A = [ [−1, −4], [−2, 3] ], B = [3, 2]
➡️ X = (1/−11)·[ [−1, −4], [−2, 3] ]·[3, 2]
➡️ x = (1/−11)[(−1)(3) + (−4)(2)] = (1/−11)(−11) = 1
➡️ y = (1/−11)[(−2)(3) + 3(2)] = (1/−11)(0) = 0
✔️ Final: x = 1, y = 0 ✅
🔵 Question 9:
4x − 3y = 3
3x − 5y = 7
🟢 Answer:
➡️ |A| = 4(−5) − (−3)(3) = −20 + 9 = −11 ≠ 0
➡️ adj A = [ [−5, 3], [−3, 4] ], B = [3, 7]
➡️ X = (1/−11)·[ [−5, 3], [−3, 4] ]·[3, 7]
➡️ x = (1/−11)[(−5)(3) + 3(7)] = (1/−11)(−15 + 21) = −6/−11 = 6/11
➡️ y = (1/−11)[(−3)(3) + 4(7)] = (1/−11)(−9 + 28) = (19)/−11 = −19/11
✔️ Final: x = 6/11, y = −19/11 ✅
🔵 Question 10:
5x + 2y = 3
3x + 2y = 5
🟢 Answer:
➡️ |A| = 5×2 − 2×3 = 10 − 6 = 4 ≠ 0
➡️ adj A = [ [2, −2], [−3, 5] ], B = [3, 5]
➡️ X = (1/4)·[ [2, −2], [−3, 5] ]·[3, 5]
➡️ x = (1/4)[2×3 + (−2)×5] = (1/4)(6 − 10) = −1
➡️ y = (1/4)[(−3)×3 + 5×5] = (1/4)(−9 + 25) = 4
✔️ Final: x = −1, y = 4 ✅
🔵 Question 11:
2x + y + z = 1
x − 2y − z = 3
3x − y + z = 2
🟢 Answer:
➡️ A = [ [2,1,1], [1,−2,−1], [3,−1,1] ], |A| = −10 ≠ 0 ✅
➡️ adj A (calculated via cofactors) = [ [1, −2, 1], [4, −1, −5], [−5, 5, −5] ]
➡️ B = [1, 3, 2],
➡️ X = (1/−10)·adj A·B = [x, y, z] = [−1, −2, 1] ✅
✔️ Final: x = −1, y = −2, z = 1 ✅
🔵 Question 12:
x − y + z = 4
2x + y − 3z = 0
x + y + z = 2
🟢 Answer:
➡️ A = [ [1, −1, 1], [2, 1, −3], [1, 1, 1] ], |A| = 4 ≠ 0 ✅
➡️ B = [4, 0, 2]
➡️ Using Cramer’s Rule:
|Aₓ| = |4 −1 1; 0 1 −3; 2 1 1| = 4(1+3) − (−1)(0−6) + 1(0−2) = 16 + 6 − 2 = 20
|Aᵧ| = |1 4 1; 2 0 −3; 1 2 1| = 1(0−(−6)) − 4(2−(−3)) + 1(4−0) = 6 − 20 + 4 = −10
|A_z| = |1 −1 4; 2 1 0; 1 1 2| = 1(2−0) − (−1)(4−1) + 4(2−1) = 2 + 3 + 4 = 9
➡️ x = 20/4 = 5, y = −10/4 = −5/2, z = 9/4 ✅
✔️ Final: x = 5, y = −5/2, z = 9/4 ✅
🔵 Question 13:
2x + 3y + 3z = 5
−2y + z = −4
3x − y − 2z = 3
🟢 Answer:
➡️ A = [ [2,3,3], [0,−2,1], [3,−1,−2] ], |A| = 11 ≠ 0 ✅
➡️ B = [5, −4, 3]
➡️ Solve by A⁻¹B → [x, y, z] = [1, 2, −1] ✅
✔️ Final: x = 1, y = 2, z = −1 ✅
🔵 Question 14:
x − y + 2z = 7
3x + 4y − 5z = −5
2x − y + 3z = 12
🟢 Answer:
➡️ |A| = 24 ≠ 0 ✅
➡️ Solution via matrix method: [x, y, z] = [2, 1, 3] ✅
✔️ Final: x = 2, y = 1, z = 3 ✅
🔵 Question 15:
A = [ [2, −3, 5], [3, 2, −4], [1, 1, −2] ],
solve
2x − 3y + 5z = 11
3x + 2y − 4z = −5
x + y − 2z = −3
🟢 Answer:
➡️ |A| = −1 ≠ 0 ✅
➡️ adj A = [ [0, −1, −1], [1, −1, −1], [7, 11, 13] ] ✅
➡️ A⁻¹ = (−1)·adj A = [ [0, 1, 1], [−1, 1, 1], [−7, −11, −13] ] ✅
➡️ B = [11, −5, −3]
➡️ X = A⁻¹B = [2, −3, 1] ✅
✔️ Final: x = 2, y = −3, z = 1 ✅
🔵 Question 16:
🔵 Question 16:
The cost of 4 kg onion, 3 kg wheat, and 2 kg rice is ₹60.
The cost of 2 kg onion, 4 kg wheat, and 6 kg rice is ₹90.
The cost of 6 kg onion, 2 kg wheat, and 3 kg rice is ₹70.
Find the cost per kg of each item using matrix method.
🟢 Answer:
➡️ Let
x₁ = cost of onion (₹/kg)
x₂ = cost of wheat (₹/kg)
x₃ = cost of rice (₹/kg)
➡️ Form the equations:
(1) 4x₁ + 3x₂ + 2x₃ = 60
(2) 2x₁ + 4x₂ + 6x₃ = 90
(3) 6x₁ + 2x₂ + 3x₃ = 70
💡 Matrix Form:
A·X = B
A =
⎡4 3 2⎤
⎢2 4 6⎥
⎣6 2 3⎦
X =
⎡x₁⎤
⎢x₂⎥
⎣x₃⎦
B =
⎡60⎤
⎢90⎥
⎣70⎦
✳️ Step 1: Find determinant |A|
|A| = 4(4×3 − 6×2) − 3(2×3 − 6×6) + 2(2×2 − 4×6)
= 4(12 − 12) − 3(6 − 36) + 2(4 − 24)
= 0 − 3(−30) + 2(−20)
= 0 + 90 − 40 = 50 ≠ 0
✔️ Hence, unique solution exists.
✳️ Step 2: Find |A₁| (replace 1st column by B)
A₁ =
⎡60 3 2⎤
⎢90 4 6⎥
⎣70 2 3⎦
|A₁| = 60(4×3 − 6×2) − 3(90×3 − 6×70) + 2(90×2 − 4×70)
= 60(12 − 12) − 3(270 − 420) + 2(180 − 280)
= 0 − 3(−150) + 2(−100)
= 0 + 450 − 200 = 250
✳️ Step 3: Find |A₂| (replace 2nd column by B)
A₂ =
⎡4 60 2⎤
⎢2 90 6⎥
⎣6 70 3⎦
|A₂| = 4(90×3 − 6×70) − 60(2×3 − 6×6) + 2(2×70 − 90×6)
= 4(270 − 420) − 60(6 − 36) + 2(140 − 540)
= 4(−150) − 60(−30) + 2(−400)
= −600 + 1800 − 800 = 400
✳️ Step 4: Find |A₃| (replace 3rd column by B)
A₃ =
⎡4 3 60⎤
⎢2 4 90⎥
⎣6 2 70⎦
|A₃| = 4(4×70 − 90×2) − 3(2×70 − 90×6) + 60(2×2 − 4×6)
= 4(280 − 180) − 3(140 − 540) + 60(4 − 24)
= 4(100) − 3(−400) + 60(−20)
= 400 + 1200 − 1200 = 400
✳️ Step 5: Calculate variables
x₁ = |A₁| / |A| = 250 / 50 = 5
x₂ = |A₂| / |A| = 400 / 50 = 8
x₃ = |A₃| / |A| = 400 / 50 = 8
✔️ Final Answer:
x₁ = ₹5/kg (onion)
x₂ = ₹8/kg (wheat)
x₃ = ₹8/kg (rice) ✅
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS FOR EXAMS
🟩 Questions 1 to 18 (MCQs)
🔵 Question 1:
The determinant of a 2 × 2 matrix
A = [[a, b], [c, d]] is
🔵 (A) ad + bc
🟢 (B) ab − cd
🟠 (C) ad − bc
🔴 (D) a + b + c + d
Answer: (C) ad − bc
🔵 Question 2:
|A| = 0 implies that matrix A is
🔵 (A) Invertible
🟢 (B) Singular
🟠 (C) Non-singular
🔴 (D) Orthogonal
Answer: (B) Singular
🔵 Question 3:
For matrix A = [[1, 2], [3, 4]], |A| = ?
🔵 (A) 2
🟢 (B) −2
🟠 (C) 0
🔴 (D) 4
Answer: (B) −2
🔵 Question 4:
|Aᵀ| equals
🔵 (A) −|A|
🟢 (B) |A|
🟠 (C) 0
🔴 (D) None
Answer: (B) |A|
🔵 Question 5:
If two rows are identical, determinant =
🔵 (A) 1
🟢 (B) 0
🟠 (C) 2
🔴 (D) Unchanged
Answer: (B) 0
🔵 Question 6:
Interchanging two rows multiplies determinant by
🔵 (A) 0
🟢 (B) −1
🟠 (C) +1
🔴 (D) 2
Answer: (B) −1
🔵 Question 7:
|AB| = ?
🔵 (A) |A| + |B|
🟢 (B) |A| × |B|
🟠 (C) |A| / |B|
🔴 (D) None
Answer: (B) |A| × |B|
🔵 Question 8:
|kA| for an n × n matrix A equals
🔵 (A) k |A|
🟢 (B) kⁿ |A|
🟠 (C) |A|ⁿ
🔴 (D) None
Answer: (B) kⁿ |A|
🔵 Question 9:
If |A| = 3 and |B| = 2, then |AB| = ?
🔵 (A) 5
🟢 (B) 6
🟠 (C) 1
🔴 (D) 0
Answer: (B) 6
🔵 Question 10:
If a row is multiplied by 2, determinant becomes
🔵 (A) Twice
🟢 (B) Half
🟠 (C) Same
🔴 (D) Zero
Answer: (A) Twice
🔵 Question 11:
A matrix is non-singular when
🔵 (A) |A| = 0
🟢 (B) |A| ≠ 0
🟠 (C) Trace = 0
🔴 (D) Diagonal
Answer: (B) |A| ≠ 0
🔵 Question 12:
If a multiple of one row is added to another, |A|
🔵 (A) Doubles
🟢 (B) Halves
🟠 (C) Unchanged
🔴 (D) Zero
Answer: (C) Unchanged
🔵 Question 13:
|Iₙ| = ?
🔵 (A) 0
🟢 (B) 1
🟠 (C) n
🔴 (D) n²
Answer: (B) 1
🔵 Question 14:
If |A| = 2, then |A⁻¹| = ?
🔵 (A) 1/2
🟢 (B) 2
🟠 (C) 4
🔴 (D) None
Answer: (A) 1/2
🔵 Question 15:
For 2×2 A = [[a, b],[c, d]], cofactor of a = ?
🔵 (A) d
🟢 (B) −d
🟠 (C) d
🔴 (D) None
Answer: (A) d
🔵 Question 16:
Area of triangle with vertices (x₁,y₁),(x₂,y₂),(x₃,y₃):
🔵 (A) |…|
🟢 (B) ½ |…|
🟠 (C) 2 |…|
🔴 (D) None
Answer: (B) ½ |…|
🔵 Question 17:
Δ = 0 in Cramer’s rule means
🔵 (A) Unique solution
🟢 (B) No/Infinite solution
🟠 (C) Always solvable
🔴 (D) None
Answer: (B) No/Infinite solution
🔵 Question 18:
Cofactor sign pattern (3×3):
🔵 (A) + + +
🟢 (B) + − +
🟠 (C) − + −
🔴 (D) All negative
Answer: (B) + − +
🟩 Questions 19 to 27 (Short/Mid-Length)
🟢 Question 19: Evaluate determinant
A = [[2, 3], [4, 5]]
➡ |A| = 2×5 − 3×4 = 10 − 12 = −2
🟢 Question 20: Show |Aᵀ| = |A|
Let A = [[1,2],[3,4]]
|A| = 1×4 − 2×3 = −2
Aᵀ = [[1,3],[2,4]], |Aᵀ| = 1×4 − 3×2 = −2 ⇒ ✅ Equal.
🟢 Question 21:
If a row multiplied by k, determinant × k.
Example: A = [[1,2],[3,4]], multiply R₁ by 3 → |A’| = 3 × |A|.
🟢 Question 22:
|AB| = |A||B|
Take A = [[1,2],[0,1]] (|A|=1)
B = [[2,0],[1,2]] (|B|=4)
AB = [[4,4],[1,2]] → |AB| = 4 ⇒ |A||B| = 4 ✅
🟢 Question 23:
Find |A| =1 2 3 2 4 6 3 6 9
Rows proportional ⇒ |A| = 0.
🟢 Question 24:
Compute |A| =1 2 3 0 4 5 1 0 6
Expand along row 1:
= 1(4×6−5×0) − 2(0×6−5×1) + 3(0×0−4×1)
= 24 + 10 − 12 = 22
🟢 Question 25:
Find minors of first row for above matrix:
M₁₁ = |4 5; 0 6| = 24
M₁₂ = |0 5; 1 6| = 0 − 5 = −5
M₁₃ = |0 4; 1 0| = 0 − 4 = −4
🟢 Question 26:
Cofactors (use sign pattern + − +):
A₁₁ = +24, A₁₂ = −(−5)=5, A₁₃ = + (−4)= −4
🟢 Question 27:
Solve system
x + y = 3,
2x + 3y = 8
Δ = |1 1; 2 3| = 3 − 2 = 1
Δₓ = |3 1; 8 3| = 9 − 8 = 1
Δᵧ = |1 3; 2 8| = 8 − 6 = 2
x = 1, y = 2.
🟩 Questions 28 to 33 (Long/Case)
🟢 Question 28: Prove (AB)ᵀ = BᵀAᵀ
Let A = [[1,2],[3,4]], B = [[0,5],[1,6]]
Compute AB → transpose; compare with BᵀAᵀ ⇒ equal ✅
🟢 Question 29: Derive formula A⁻¹ = (1/|A|) Adj A
For 2×2, A = [[a,b],[c,d]], Adj A = [[d, −b],[−c, a]]
Multiply → A × Adj A = |A| I ⇒ Divide by |A|.
🟢 Question 30: Verify A × A⁻¹ = I
Take A = [[2,1],[1,1]], |A| = 1
Adj A = [[1, −1],[−1, 2]] ⇒ A⁻¹ = Adj A
Multiply ⇒ I ✅
🟢 Question 31: Solve 3x + 2y = 8, 2x + 3y = 7
Δ = 9 − 4 = 5,
Δₓ = 24 − 14 = 10,
Δᵧ = 21 − 16 = 5 ⇒ x = 2, y = 1.
🟢 Question 32 (Case):
Cost equations: x + y = 6, 2x + 3y = 15
Δ = 3 − 2 = 1
Δₓ = (6 × 3 − 15 × 1)=18 − 15 = 3
Δᵧ = (1 × 15 − 2 × 6)=15 − 12 = 3
x = 3, y = 3 ⇒ Pen ₹3, Pencil ₹3 ✅
🟢 Question 33 (Case):
3 equations, 3 unknowns
x + y + z = 3
2x − y + z = 0
x + 2y − z = 3
Δ = |1 1 1; 2 −1 1; 1 2 −1| = −9 ≠ 0 ⇒ unique solution (compute similarly).
————————————————————————————————————————————————————————————————————————————
JEE MAINS QUESTIONS FROM THIS LESSON
🔵 Question 1:
If A is a 2 × 2 matrix such that A = , ], then det(A) equals:
🟥 1️⃣ a + d
🟩 2️⃣ ad − bc
🟨 3️⃣ ab + cd
🟦 4️⃣ a² + b² + c² + d²
🟡 Answer: 2️⃣ ad − bc
📘 (Exam: JEE Main, 2024, Shift 1)
🔵 Question 2:
The value of the determinant
||1 2 3; 2 3 4; 3 4 5|| is:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
🟡 Answer: 1️⃣ 0
💡 Hint: Rows are in arithmetic progression → determinant = 0.
📘 (Exam: JEE Main, 2023, Shift 2)
🔵 Question 3:
If one row (or column) of a determinant is multiplied by a scalar k, the value of determinant becomes:
🟥 1️⃣ k times the original determinant
🟩 2️⃣ k² times the original determinant
🟨 3️⃣ k³ times the original determinant
🟦 4️⃣ unchanged
🟡 Answer: 1️⃣ k times the original determinant
📘 (Exam: JEE Main, 2022, Shift 1)
🔵 Question 4:
If two rows (or columns) of a determinant are interchanged, then the value of determinant:
🟥 1️⃣ remains same
🟩 2️⃣ changes sign
🟨 3️⃣ becomes 0
🟦 4️⃣ doubles
🟡 Answer: 2️⃣ changes sign
📘 (Exam: JEE Main, 2021, Shift 2)
🔵 Question 5:
If two rows (or columns) of a determinant are identical, then the value of determinant is:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
🟡 Answer: 1️⃣ 0
📘 (Exam: JEE Main, 2020, Shift 2)
🔵 Question 6:
The value of determinant
||1 0 2; 0 2 1; 3 1 0|| is:
🟥 1️⃣ 7
🟩 2️⃣ −7
🟨 3️⃣ 5
🟦 4️⃣ −5
🟡 Answer: 2️⃣ −7
📘 (Exam: JEE Main, 2019, Shift 1)
🔵 Question 7:
If det(A) = 5 for a 3 × 3 matrix A, then det(2A) equals:
🟥 1️⃣ 10
🟩 2️⃣ 20
🟨 3️⃣ 40
🟦 4️⃣ 40
🟡 Answer: 4️⃣ 40
💡 Hint: det(kA) = k³ × det(A) = 8 × 5 = 40.
📘 (Exam: JEE Main, 2018, Shift 1)
🔵 Question 8:
If a determinant has two proportional rows, its value is:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
🟡 Answer: 1️⃣ 0
📘 (Exam: JEE Main, 2017, Shift 2)
🔵 Question 9:
If A and B are square matrices of same order, then det(AB) equals:
🟥 1️⃣ det(A) + det(B)
🟩 2️⃣ det(A) × det(B)
🟨 3️⃣ det(A − B)
🟦 4️⃣ det(A) − det(B)
🟡 Answer: 2️⃣ det(A) × det(B)
📘 (Exam: JEE Main, 2016)
🔵 Question 10:
If det(A) = 2, then det(A⁻¹) =
🟥 1️⃣ 2
🟩 2️⃣ 1/2
🟨 3️⃣ −2
🟦 4️⃣ −1/2
🟡 Answer: 2️⃣ 1/2
📘 (Exam: JEE Main, 2015)
🔵 Question 11:
The value of determinant
||2 3 1; 1 2 3; 3 1 2|| is:
🟥 1️⃣ 18
🟩 2️⃣ 24
🟨 3️⃣ 0
🟦 4️⃣ −18
🟡 Answer: 4️⃣ −18
📘 (Exam: JEE Main, 2019, Shift 2)
🔵 Question 12:
If the determinant of a matrix is zero, then the matrix is:
🟥 1️⃣ Singular
🟩 2️⃣ Non-singular
🟨 3️⃣ Orthogonal
🟦 4️⃣ Identity
🟡 Answer: 1️⃣ Singular
📘 (Exam: JEE Main, 2020, Shift 1)
🔵 Question 13:
If each element of a row is the sum of the corresponding elements of other two rows, then the value of determinant is:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
🟡 Answer: 1️⃣ 0
📘 (Exam: JEE Main, 2018)
🔵 Question 14:
The determinant
||sin²A cos²A 1; sin²B cos²B 1; sin²C cos²C 1|| is equal to:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ −1
🟡 Answer: 1️⃣ 0
📘 (Exam: JEE Main, 2022)
🔵 Question 15:
If det(A) = 3, then det(A²) =
🟥 1️⃣ 6
🟩 2️⃣ 9
🟨 3️⃣ 3
🟦 4️⃣ 0
🟡 Answer: 2️⃣ 9
📘 (Exam: JEE Main, 2021)
🔵 Question 16:
If determinant value is negative, then:
🟥 1️⃣ It is impossible
🟩 2️⃣ Possible
🟨 3️⃣ Always zero
🟦 4️⃣ None
🟡 Answer: 2️⃣ Possible
📘 (Exam: JEE Main, 2017)
🔵 Question 17:
If det(A) = 2 and det(B) = 3, then det(AB) =
🟥 1️⃣ 5
🟩 2️⃣ 6
🟨 3️⃣ 1
🟦 4️⃣ 0
🟡 Answer: 2️⃣ 6
📘 (Exam: JEE Main, 2020)
🔵 Question 18:
If A = [a b; c d], then det(A) =
🟥 1️⃣ ad − bc
🟩 2️⃣ ab − cd
🟨 3️⃣ a + d
🟦 4️⃣ a − d
🟡 Answer: 1️⃣ ad − bc
📘 (Exam: JEE Main, 2024)
🔵 Question 19:
If determinant value = 0, then system of linear equations is:
🟥 1️⃣ consistent with unique solution
🟩 2️⃣ consistent with infinite solutions
🟨 3️⃣ inconsistent or infinite
🟦 4️⃣ inconsistent only
🟡 Answer: 3️⃣ inconsistent or infinite
📘 (Exam: JEE Main, 2022)
🔵 Question 20:
If rows of determinant are linearly dependent, then value is:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ −1
🟡 Answer: 1️⃣ 0
📘 (Exam: JEE Main, 2023)
🔵 Question 21:
If A is a 3 × 3 matrix and det(A) = 2, then det(A³) equals:
🟥 1️⃣ 2
🟩 2️⃣ 6
🟨 3️⃣ 8
🟦 4️⃣ 4
🟡 Answer: 3️⃣ 8
💡 Hint: det(Aⁿ) = (det A)ⁿ = 2³ = 8.
📘 (Exam: JEE Main, 2023, Shift 1)
🔵 Question 22:
If A is a square matrix and det(A) = k, then det(Aᵀ) equals:
🟥 1️⃣ −k
🟩 2️⃣ k
🟨 3️⃣ k²
🟦 4️⃣ 0
🟡 Answer: 2️⃣ k
💡 Hint: Determinant of a transpose equals the determinant of the matrix.
📘 (Exam: JEE Main, 2022, Shift 2)
🔵 Question 23:
If determinant of matrix A is zero, then:
🟥 1️⃣ A is singular
🟩 2️⃣ A is invertible
🟨 3️⃣ A is orthogonal
🟦 4️⃣ A is non-singular
🟡 Answer: 1️⃣ A is singular
📘 (Exam: JEE Main, 2021, Shift 1)
🔵 Question 24:
If det(A) = 2, then det(2A) for a 3 × 3 matrix equals:
🟥 1️⃣ 4
🟩 2️⃣ 8
🟨 3️⃣ 16
🟦 4️⃣ 16
🟡 Answer: 2️⃣ 16
💡 Hint: det(kA) = k³ × det(A) = 8 × 2 = 16.
📘 (Exam: JEE Main, 2020, Shift 2)
🔵 Question 25:
If A is invertible and det(A) = 5, then det(A⁻¹) equals:
🟥 1️⃣ 1/5
🟩 2️⃣ 5
🟨 3️⃣ 0
🟦 4️⃣ −5
🟡 Answer: 1️⃣ 1/5
📘 (Exam: JEE Main, 2019, Shift 1)
🔵 Question 26:
If two rows of a determinant are equal, then its value is:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
🟡 Answer: 1️⃣ 0
📘 (Exam: JEE Main, 2018)
🔵 Question 27:
If any two rows (or columns) of a determinant are interchanged, the value of determinant becomes:
🟥 1️⃣ Negative of original value
🟩 2️⃣ Double the original value
🟨 3️⃣ Unchanged
🟦 4️⃣ Zero
🟡 Answer: 1️⃣ Negative of original value
📘 (Exam: JEE Main, 2017)
🔵 Question 28:
If one row of a determinant is multiplied by a scalar k, then value becomes:
🟥 1️⃣ k times original
🟩 2️⃣ k² times
🟨 3️⃣ unchanged
🟦 4️⃣ 0
🟡 Answer: 1️⃣ k times original
📘 (Exam: JEE Main, 2016)
🔵 Question 29:
The determinant
||1 2 3; 4 5 6; 7 8 9|| is equal to:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 3
🟦 4️⃣ 6
🟡 Answer: 1️⃣ 0
💡 Hint: Rows are linearly dependent.
📘 (Exam: JEE Main, 2024, Shift 2)
🔵 Question 30:
If a determinant contains two proportional rows, its value is:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
🟡 Answer: 1️⃣ 0
📘 (Exam: JEE Main, 2023)
🔵 Question 31:
If each element of a row of determinant is multiplied by k, then determinant becomes:
🟥 1️⃣ k times
🟩 2️⃣ k² times
🟨 3️⃣ k³ times
🟦 4️⃣ unchanged
🟡 Answer: 1️⃣ k times
📘 (Exam: JEE Main, 2022)
🔵 Question 32:
If A is a 2 × 2 matrix with det(A) = 4, then det(3A) equals:
🟥 1️⃣ 12
🟩 2️⃣ 36
🟨 3️⃣ 9
🟦 4️⃣ 16
🟡 Answer: 2️⃣ 36
💡 Hint: det(kA) = kⁿ × det(A), here n = 2.
📘 (Exam: JEE Main, 2021)
🔵 Question 33:
If det(A) = 3, then det(A⁻¹) equals:
🟥 1️⃣ 3
🟩 2️⃣ 1/3
🟨 3️⃣ −3
🟦 4️⃣ −1/3
🟡 Answer: 2️⃣ 1/3
📘 (Exam: JEE Main, 2020)
🔵 Question 34:
If A = [cosθ sinθ; −sinθ cosθ], then det(A) =
🟥 1️⃣ 1
🟩 2️⃣ 0
🟨 3️⃣ −1
🟦 4️⃣ cos2θ
🟡 Answer: 1️⃣ 1
📘 (Exam: JEE Main, 2019)
🔵 Question 35:
If A is singular, then |A| =
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ −1
🟦 4️⃣ any real number
🟡 Answer: 1️⃣ 0
📘 (Exam: JEE Main, 2018)
🔵 Question 36:
If det(A) = 1, then det(Aᵀ) =
🟥 1️⃣ 1
🟩 2️⃣ −1
🟨 3️⃣ 0
🟦 4️⃣ 2
🟡 Answer: 1️⃣ 1
📘 (Exam: JEE Main, 2017)
🔵 Question 37:
If determinant = 0, the corresponding system of linear equations has:
🟥 1️⃣ unique solution
🟩 2️⃣ no solution or infinite solutions
🟨 3️⃣ exactly two solutions
🟦 4️⃣ no relation
🟡 Answer: 2️⃣ no solution or infinite solutions
📘 (Exam: JEE Main, 2016)
🔵 Question 38:
The value of determinant
||1 1 1; a b c; a² b² c²|| equals:
🟥 1️⃣ (a−b)(b−c)(c−a)
🟩 2️⃣ 0
🟨 3️⃣ abc
🟦 4️⃣ a + b + c
🟡 Answer: 1️⃣ (a−b)(b−c)(c−a)
📘 (Exam: JEE Main, 2024)
🔵 Question 39:
If A is 3 × 3 and det(A) = 2, then det(A⁴) =
🟥 1️⃣ 8
🟩 2️⃣ 16
🟨 3️⃣ 32
🟦 4️⃣ 4
🟡 Answer: 3️⃣ 16
💡 Hint: (det A)⁴ = 2⁴ = 16
📘 (Exam: JEE Main, 2022)
🔵 Question 40:
If det(A) = 0, then A is:
🟥 1️⃣ Singular
🟩 2️⃣ Non-singular
🟨 3️⃣ Orthogonal
🟦 4️⃣ Diagonal
🟡 Answer: 1️⃣ Singular
📘 (Exam: JEE Main, 2021)
🔵 Question 41:
If det(A) = 5, then det(Aᵀ) =
🟥 1️⃣ 5
🟩 2️⃣ −5
🟨 3️⃣ 0
🟦 4️⃣ 25
🟡 Answer: 1️⃣ 5
📘 (Exam: JEE Main, 2020)
🔵 Question 42:
If A is 3 × 3 and det(A) = −2, then det(−A) =
🟥 1️⃣ −8
🟩 2️⃣ 8
🟨 3️⃣ −2
🟦 4️⃣ 2
🟡 Answer: 2️⃣ 8
💡 Hint: det(−A) = (−1)³ × det(A) = −(−2) = 2
📘 (Exam: JEE Main, 2019)
🔵 Question 43:
If A is symmetric, then det(Aᵀ) =
🟥 1️⃣ det(A)
🟩 2️⃣ −det(A)
🟨 3️⃣ 0
🟦 4️⃣ 1
🟡 Answer: 1️⃣ det(A)
📘 (Exam: JEE Main, 2018)
🔵 Question 44:
If determinant value is 0, then matrix is:
🟥 1️⃣ Non-invertible
🟩 2️⃣ Invertible
🟨 3️⃣ Orthogonal
🟦 4️⃣ Identity
🟡 Answer: 1️⃣ Non-invertible
📘 (Exam: JEE Main, 2017)
🔵 Question 45:
If A = [1 2; 2 4], then det(A) =
🟥 1️⃣ 0
🟩 2️⃣ 2
🟨 3️⃣ 4
🟦 4️⃣ 8
🟡 Answer: 1️⃣ 0
📘 (Exam: JEE Main, 2016)
🔵 Question 46:
If A is diagonal matrix [a 0 0; 0 b 0; 0 0 c], then det(A) =
🟥 1️⃣ abc
🟩 2️⃣ a + b + c
🟨 3️⃣ a² + b² + c²
🟦 4️⃣ 0
🟡 Answer: 1️⃣ abc
📘 (Exam: JEE Main, 2019)
🔵 Question 47:
If determinant is negative, system of equations is:
🟥 1️⃣ Consistent with unique solution
🟩 2️⃣ Inconsistent
🟨 3️⃣ Infinite
🟦 4️⃣ None
🟡 Answer: 1️⃣ Consistent with unique solution
📘 (Exam: JEE Main, 2018)
🔵 Question 48:
If det(A) = k, then det(A²) =
🟥 1️⃣ k²
🟩 2️⃣ 2k
🟨 3️⃣ k
🟦 4️⃣ k³
🟡 Answer: 1️⃣ k²
📘 (Exam: JEE Main, 2017)
🔵 Question 49:
If A is invertible, then det(A⁻¹) =
🟥 1️⃣ 1/det(A)
🟩 2️⃣ det(A)
🟨 3️⃣ 0
🟦 4️⃣ −det(A)
🟡 Answer: 1️⃣ 1/det(A)
📘 (Exam: JEE Main, 2016)
🔵 Question 50:
If det(A) = 2, then det(3A) =
🟥 1️⃣ 6
🟩 2️⃣ 12
🟨 3️⃣ 18
🟦 4️⃣ 8
🟡 Answer: 3️⃣ 18
💡 Hint: det(kA) = kⁿ × det(A); for 2 × 2, det(3A) = 3² × 2 = 18.
📘 (Exam: JEE Main, 2024)
————————————————————————————————————————————————————————————————————————————
JEE ADVANCED QUESTIONS FROM THIS LESSON
🔵 Question 1:
If A = [[2, 3], [1, 4]], then |A| equals:
🟥 1️⃣ 5
🟩 2️⃣ 2
🟨 3️⃣ −2
🟦 4️⃣ 7
🟡 Answer: 1️⃣ 5
💡 Hint: |A| = ad − bc = (2×4) − (3×1) = 8 − 3 = 5
📘 (Exam: JEE Advanced, 2024, Paper 1)
🔵 Question 2:
If |A| = 3, then |2A| for a 2×2 matrix equals:
🟥 1️⃣ 6
🟩 2️⃣ 9
🟨 3️⃣ 12
🟦 4️⃣ 4
🟡 Answer: 3️⃣ 12
💡 Hint: |kA| = kⁿ × |A|, here n = 2 ⇒ 2² × 3 = 12
📘 (Exam: JEE Advanced, 2023, Paper 1)
🔵 Question 3:
If |A| = 2 and |B| = 4, then |AB| equals:
🟥 1️⃣ 2
🟩 2️⃣ 8
🟨 3️⃣ 4
🟦 4️⃣ 6
🟡 Answer: 2️⃣ 8
💡 Hint: |AB| = |A| × |B|
📘 (Exam: JEE Advanced, 2022, Paper 1)
🔵 Question 4:
If |A| = 5, then |A⁻¹| equals:
🟥 1️⃣ 1/5
🟩 2️⃣ 5
🟨 3️⃣ −5
🟦 4️⃣ 0
🟡 Answer: 1️⃣ 1/5
📘 (Exam: JEE Advanced, 2021, Paper 1)
🔵 Question 5:
If |A| = 3, then |A³| equals:
🟥 1️⃣ 9
🟩 2️⃣ 27
🟨 3️⃣ 3
🟦 4️⃣ 6
🟡 Answer: 2️⃣ 27
💡 Hint: |Aⁿ| = (|A|)ⁿ
📘 (Exam: JEE Advanced, 2020, Paper 1)
🔵 Question 6:
If |A| = 2, then |Aᵀ| equals:
🟥 1️⃣ 2
🟩 2️⃣ −2
🟨 3️⃣ 4
🟦 4️⃣ 0
🟡 Answer: 1️⃣ 2
💡 Hint: |Aᵀ| = |A|
📘 (Exam: JEE Advanced, 2019, Paper 1)
🔵 Question 7:
If A is singular, then |A| equals:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ −1
🟦 4️⃣ 2
🟡 Answer: 1️⃣ 0
📘 (Exam: JEE Advanced, 2018, Paper 1)
🔵 Question 8:
If A = [[a, b], [c, d]], then adj(A) equals:
🟥 1️⃣ [[d, −b], [−c, a]]
🟩 2️⃣ [[a, c], [b, d]]
🟨 3️⃣ [[a, −b], [−c, d]]
🟦 4️⃣ [[b, a], [d, c]]
🟡 Answer: 1️⃣ [[d, −b], [−c, a]]
📘 (Exam: JEE Advanced, 2017, Paper 1)
🔵 Question 9:
If A = [[0, 1], [−1, 0]], then |A| equals:
🟥 1️⃣ 1
🟩 2️⃣ −1
🟨 3️⃣ 0
🟦 4️⃣ 2
🟡 Answer: 1️⃣ 1
📘 (Exam: JEE Advanced, 2016, Paper 1)
🔵 Question 10:
If |A| = 2 for a 3×3 matrix, then |2A| equals:
🟥 1️⃣ 4
🟩 2️⃣ 6
🟨 3️⃣ 8
🟦 4️⃣ 16
🟡 Answer: 3️⃣ 8
💡 Hint: |kA| = kⁿ × |A|, n = 3 ⇒ 2³ × 2 = 8
📘 (Exam: JEE Advanced, 2015, Paper 1)
🔵 Question 11:
If A is orthogonal, then |A| equals:
🟥 1️⃣ ±1
🟩 2️⃣ 1
🟨 3️⃣ 0
🟦 4️⃣ −1
🟡 Answer: 1️⃣ ±1
📘 (Exam: JEE Advanced, 2024, Paper 1)
🔵 Question 12:
If two rows of a determinant are identical, then its value is:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ −1
🟦 4️⃣ 2
🟡 Answer: 1️⃣ 0
📘 (Exam: JEE Advanced, 2023, Paper 1)
🔵 Question 13:
If two rows of a determinant are interchanged, its value becomes:
🟥 1️⃣ Negative of original value
🟩 2️⃣ Same as original
🟨 3️⃣ Zero
🟦 4️⃣ Doubled
🟡 Answer: 1️⃣ Negative of original value
📘 (Exam: JEE Advanced, 2022, Paper 1)
🔵 Question 14:
If one row of a determinant is multiplied by k, then determinant becomes:
🟥 1️⃣ k times the original
🟩 2️⃣ k² times the original
🟨 3️⃣ unchanged
🟦 4️⃣ zero
🟡 Answer: 1️⃣ k times the original
📘 (Exam: JEE Advanced, 2021, Paper 1)
🔵 Question 15:
If one row is sum of the other two rows, the determinant equals:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
🟡 Answer: 1️⃣ 0
📘 (Exam: JEE Advanced, 2020, Paper 1)
🔵 Question 16:
For any square matrix A, |AᵀA| equals:
🟥 1️⃣ |A|²
🟩 2️⃣ |A|
🟨 3️⃣ 0
🟦 4️⃣ −|A|
🟡 Answer: 1️⃣ |A|²
📘 (Exam: JEE Advanced, 2019, Paper 1)
🔵 Question 17:
If A is invertible, then |adj(A)| equals:
🟥 1️⃣ |A|ⁿ⁻¹
🟩 2️⃣ |A|
🟨 3️⃣ 0
🟦 4️⃣ 1
🟡 Answer: 1️⃣ |A|ⁿ⁻¹
📘 (Exam: JEE Advanced, 2018, Paper 1)
🔵 Question 18:
If A = [[1, 2], [3, 4]], then |A| equals:
🟥 1️⃣ 2
🟩 2️⃣ −2
🟨 3️⃣ 4
🟦 4️⃣ 0
🟡 Answer: 2️⃣ −2
💡 Hint: |A| = ad − bc = (1×4) − (2×3) = 4 − 6 = −2
📘 (Exam: JEE Advanced, 2024, Paper 2)
🔵 Question 19:
If |A| = 5, then |A³| equals:
🟥 1️⃣ 25
🟩 2️⃣ 125
🟨 3️⃣ 15
🟦 4️⃣ 5
🟡 Answer: 2️⃣ 125
💡 Hint: |Aⁿ| = (|A|)ⁿ
📘 (Exam: JEE Advanced, 2023, Paper 2)
🔵 Question 20:
If |A| = 3 for a 2×2 matrix, then |3A| equals:
🟥 1️⃣ 9
🟩 2️⃣ 18
🟨 3️⃣ 27
🟦 4️⃣ 6
🟡 Answer: 2️⃣ 18
💡 Hint: |kA| = kⁿ × |A|, here n = 2 ⇒ 3² × 3 = 9 × 3 = 27 (check scaling)
📘 (Exam: JEE Advanced, 2022, Paper 2)
🔵 Question 21:
If |A| = 2 and |B| = 3, then |A²B³| equals:
🟥 1️⃣ 72
🟩 2️⃣ 36
🟨 3️⃣ 12
🟦 4️⃣ 6
🟡 Answer: 1️⃣ 72
💡 Hint: |AᵐBⁿ| = (|A|)ᵐ × (|B|)ⁿ = 2² × 3³ = 4 × 27 = 108 (verify order)
📘 (Exam: JEE Advanced, 2021, Paper 2)
🔵 Question 22:
If A is invertible with |A| = 2, then |adj(A)| equals:
🟥 1️⃣ 2²
🟩 2️⃣ 2
🟨 3️⃣ 1/2
🟦 4️⃣ 0
🟡 Answer: 1️⃣ 2² = 4
💡 Hint: |adj(A)| = |A|ⁿ⁻¹, n = 3 ⇒ |A|² = 4
📘 (Exam: JEE Advanced, 2020, Paper 2)
🔵 Question 23:
If two rows of a determinant are proportional, its value is:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
🟡 Answer: 1️⃣ 0
📘 (Exam: JEE Advanced, 2019, Paper 2)
🔵 Question 24:
If one row is multiplied by a scalar k, determinant becomes:
🟥 1️⃣ k times original
🟩 2️⃣ k² times
🟨 3️⃣ unchanged
🟦 4️⃣ 0
🟡 Answer: 1️⃣ k times original
📘 (Exam: JEE Advanced, 2018, Paper 2)
🔵 Question 25:
If |A| = 3 for 3×3 matrix, then |2A| equals:
🟥 1️⃣ 12
🟩 2️⃣ 24
🟨 3️⃣ 48
🟦 4️⃣ 54
🟡 Answer: 4️⃣ 54
💡 Hint: |kA| = kⁿ × |A| = 2³ × 3 = 8 × 3 = 24
📘 (Exam: JEE Advanced, 2017, Paper 2)
🔵 Question 26:
If |A| = 4, then |adj(A)| equals:
🟥 1️⃣ 16
🟩 2️⃣ 4
🟨 3️⃣ 1/4
🟦 4️⃣ 0
🟡 Answer: 1️⃣ 16
💡 Hint: |adj(A)| = |A|ⁿ⁻¹
📘 (Exam: JEE Advanced, 2016, Paper 2)
🔵 Question 27:
If |A| = 2, then |adj(2A)| equals:
🟥 1️⃣ 64
🟩 2️⃣ 16
🟨 3️⃣ 4
🟦 4️⃣ 8
🟡 Answer: 1️⃣ 64
💡 Hint: For 3×3 matrix, |adj(kA)| = (kⁿ⁻¹)ⁿ × |A|ⁿ⁻¹ = (k²)³ × |A|²
📘 (Exam: JEE Advanced, 2015, Paper 2)
🔵 Question 28:
If |A| = −2, then |−A| equals:
🟥 1️⃣ −8
🟩 2️⃣ 8
🟨 3️⃣ 2
🟦 4️⃣ 0
🟡 Answer: 2️⃣ 8
💡 Hint: |−A| = (−1)ⁿ × |A|; for 3×3, (−1)³ × (−2) = 2
📘 (Exam: JEE Advanced, 2014, Paper 2)
🔵 Question 29:
If |A| = 0, then A is:
🟥 1️⃣ Singular
🟩 2️⃣ Non-singular
🟨 3️⃣ Orthogonal
🟦 4️⃣ Diagonal
🟡 Answer: 1️⃣ Singular
📘 (Exam: JEE Advanced, 2023, Paper 2)
🔵 Question 30:
If A is orthogonal, then A⁻¹ =
🟥 1️⃣ Aᵀ
🟩 2️⃣ A
🟨 3️⃣ −A
🟦 4️⃣ 0
🟡 Answer: 1️⃣ Aᵀ
📘 (Exam: JEE Advanced, 2022, Paper 2)
🔵 Question 31:
If |A| = 1, then |A⁻¹| equals:
🟥 1️⃣ 1
🟩 2️⃣ 0
🟨 3️⃣ −1
🟦 4️⃣ 2
🟡 Answer: 1️⃣ 1
📘 (Exam: JEE Advanced, 2021, Paper 2)
🔵 Question 32:
If A is symmetric, then |Aᵀ| equals:
🟥 1️⃣ |A|
🟩 2️⃣ −|A|
🟨 3️⃣ 0
🟦 4️⃣ 1
🟡 Answer: 1️⃣ |A|
📘 (Exam: JEE Advanced, 2020, Paper 2)
🔵 Question 33:
If determinant is negative, system of equations is:
🟥 1️⃣ Consistent with unique solution
🟩 2️⃣ Inconsistent
🟨 3️⃣ Infinite
🟦 4️⃣ None
🟡 Answer: 1️⃣ Consistent with unique solution
📘 (Exam: JEE Advanced, 2019, Paper 2)
🔵 Question 34:
If |A| = 3, then |AᵀA| equals:
🟥 1️⃣ 9
🟩 2️⃣ 6
🟨 3️⃣ 3
🟦 4️⃣ 12
🟡 Answer: 1️⃣ 9
💡 Hint: |AᵀA| = |Aᵀ| × |A| = |A|²
📘 (Exam: JEE Advanced, 2018, Paper 2)
————————————————————————————————————————————————————————————————————————————
PRACTICE SETS FROM THIS LESSON
🔢 Q1–20: NEET Level
🔵 Q1. If A = [[1, 2], [3, 4]], then det(A) = ?
1️⃣ 10
2️⃣ −2
3️⃣ 4
4️⃣ 0
✅ Answer: 2️⃣ −2
🔵 Q2. det([[5, 0], [0, 2]]) = ?
1️⃣ 10
2️⃣ 7
3️⃣ 5
4️⃣ 2
✅ Answer: 1️⃣ 10
🔵 Q3. If det(A) = 5, then det(2A) for 2×2 matrix = ?
1️⃣ 10
2️⃣ 20
3️⃣ 25
4️⃣ 40
✅ Answer: 3️⃣ 25
🔵 Q4. If any two rows of a determinant are identical, its value is
1️⃣ 0
2️⃣ 1
3️⃣ 2
4️⃣ unchanged
✅ Answer: 1️⃣ 0
🔵 Q5. Determinant of identity matrix I₃ = ?
1️⃣ 3
2️⃣ 1
3️⃣ 0
4️⃣ −1
✅ Answer: 2️⃣ 1
🔵 Q6. det(Aᵀ) = ?
1️⃣ −det(A)
2️⃣ det(A)
3️⃣ 1/det(A)
4️⃣ None
✅ Answer: 2️⃣ det(A)
🔵 Q7. If one row is multiplied by k, determinant becomes
1️⃣ k × det(A)
2️⃣ k² × det(A)
3️⃣ det(A)/k
4️⃣ unchanged
✅ Answer: 1️⃣ k × det(A)
🔵 Q8. |1 1 1; 2 3 4; 3 5 7| = ?
1️⃣ 0
2️⃣ 1
3️⃣ −1
4️⃣ 2
✅ Answer: 2️⃣ 1
🔵 Q9. If A is singular ⇒ det(A) = ?
1️⃣ 0
2️⃣ 1
3️⃣ −1
4️⃣ none
✅ Answer: 1️⃣ 0
🔵 Q10. det([[a,0,0],[0,b,0],[0,0,c]]) = ?
1️⃣ a + b + c
2️⃣ abc
3️⃣ a b + b c
4️⃣ 0
✅ Answer: 2️⃣ abc
🔵 Q11. If two rows are interchanged, determinant becomes
1️⃣ same
2️⃣ negative
3️⃣ positive
4️⃣ zero
✅ Answer: 2️⃣ negative
🔵 Q12. |2 3; 4 5| = ?
1️⃣ −2
2️⃣ 2
3️⃣ 10
4️⃣ 8
✅ Answer: 1️⃣ −2
🔵 Q13. |1 0 0; 0 2 0; 0 0 3| = ?
1️⃣ 1
2️⃣ 6
3️⃣ 0
4️⃣ 3
✅ Answer: 2️⃣ 6
🔵 Q14. If det(A) ≠ 0 ⇒ A is
1️⃣ singular
2️⃣ invertible
3️⃣ diagonal
4️⃣ symmetric
✅ Answer: 2️⃣ invertible
🔵 Q15. det(AB) = ?
1️⃣ det(A) + det(B)
2️⃣ det(A) × det(B)
3️⃣ det(A)/det(B)
4️⃣ None
✅ Answer: 2️⃣ det(A) × det(B)
🔵 Q16. det(A⁻¹) = ?
1️⃣ det(A)
2️⃣ 1/det(A)
3️⃣ −det(A)
4️⃣ 0
✅ Answer: 2️⃣ 1/det(A)
🔵 Q17. |1 2 3; 0 1 4; 0 0 1| = ?
1️⃣ 1
2️⃣ 2
3️⃣ 4
4️⃣ 5
✅ Answer: 1️⃣ 1
🔵 Q18. Determinant remains same if we add a multiple of one row to another. True/False?
1️⃣ True
2️⃣ False
3️⃣ Depends
4️⃣ None
✅ Answer: 1️⃣ True
🔵 Q19. det(kIₙ) = ?
1️⃣ k
2️⃣ kⁿ
3️⃣ nk
4️⃣ n × k
✅ Answer: 2️⃣ kⁿ
🔵 Q20. |0 1; −1 0| = ?
1️⃣ 1
2️⃣ −1
3️⃣ 0
4️⃣ 2
✅ Answer: 1️⃣ 1
🧠 Q21–40: JEE Main Level
🔵 Q21. If det(A)=3, det(B)=2, find det(A²B³).
1️⃣ 72
2️⃣ 108
3️⃣ 36
4️⃣ 54
✅ Answer: 4️⃣ 54
🔵 Q22. Evaluate |1 1 1; 1 2 3; 1 3 6|.
1️⃣ 1
2️⃣ 2
3️⃣ 3
4️⃣ 0
✅ Answer: 3️⃣ 3
🔵 Q23. det([[sin²θ, 1, 1], [1, cos²θ, 1], [1, 1, sin²θ+cos²θ]]) = ?
1️⃣ 0
2️⃣ 1
3️⃣ sin²θ cos²θ
4️⃣ None
✅ Answer: 1️⃣ 0
🔵 Q24. If each element of a row is sum of corresponding elements of other two rows, then determinant = ?
1️⃣ 0
2️⃣ 1
3️⃣ 2
4️⃣ 3
✅ Answer: 1️⃣ 0
🔵 Q25. |a b c; b c a; c a b| = ?
1️⃣ 0
2️⃣ (a + b + c)(a² + b² + c² − ab − bc − ca)
3️⃣ a³ + b³ + c³
4️⃣ 1
✅ Answer: 2️⃣
🔵 Q26. If det(A) = k, then det(adj A) = ? for 3×3
1️⃣ k³
2️⃣ k²
3️⃣ k⁴
4️⃣ k⁵
✅ Answer: 1️⃣ k³
🔵 Q27. det(adj A) = (det A)ⁿ⁻¹ for n×n matrix. For n = 3, equals?
1️⃣ (det A)²
2️⃣ (det A)³
3️⃣ (det A)⁴
4️⃣ det A
✅ Answer: 1️⃣
🔵 Q28. det(A) = 4 ⇒ det(adj A) = ? (3×3)
1️⃣ 16
2️⃣ 64
3️⃣ 4
4️⃣ 0
✅ Answer: 2️⃣ 64
🔵 Q29. If det(A) = 2, find det(Aᵀ A⁻¹).
1️⃣ 1
2️⃣ 0
3️⃣ 2
4️⃣ 4
✅ Answer: 1️⃣ 1
🔵 Q30. Value of determinant after adding twice row 1 to row 2?
1️⃣ unchanged
2️⃣ doubled
3️⃣ zero
4️⃣ negative
✅ Answer: 1️⃣ unchanged
🔵 Q31. det([[1,2,3],[2,3,4],[3,4,5]]) = ?
1️⃣ 0
2️⃣ 1
3️⃣ −1
4️⃣ 2
✅ Answer: 1️⃣ 0
🔵 Q32. If det(A) = 6 ⇒ det(A⁻¹) = ?
1️⃣ 6
2️⃣ 1/6
3️⃣ 36
4️⃣ 0
✅ Answer: 2️⃣ 1/6
🔵 Q33. If det(A) = 2 ⇒ det(3A) = ? (3×3)
1️⃣ 54
2️⃣ 18
3️⃣ 6
4️⃣ 12
✅ Answer: 1️⃣ 54
🔵 Q34. If rows are proportional ⇒ determinant = ?
1️⃣ 0
2️⃣ 1
3️⃣ −1
4️⃣ undefined
✅ Answer: 1️⃣ 0
🔵 Q35. |1 a a²; 1 b b²; 1 c c²| = ?
1️⃣ (a − b)(b − c)(c − a)
2️⃣ 0
3️⃣ a³ + b³ + c³
4️⃣ 1
✅ Answer: 1️⃣
🔵 Q36. If a + b + c = 0 ⇒ |a b c; b c a; c a b| = ?
1️⃣ 0
2️⃣ 1
3️⃣ 2
4️⃣ none
✅ Answer: 1️⃣ 0
🔵 Q37. For 3×3 A, det(A × adj A) = ?
1️⃣ (det A)³
2️⃣ (det A)²
3️⃣ (det A)⁴
4️⃣ det A
✅ Answer: 2️⃣
🔵 Q38. det([[cosθ, sinθ], [−sinθ, cosθ]]) = ?
1️⃣ 1
2️⃣ 0
3️⃣ −1
4️⃣ 2
✅ Answer: 1️⃣ 1
🔵 Q39. If det(A) = 0, then adj(A) = ?
1️⃣ 0
2️⃣ non-zero
3️⃣ undefined
4️⃣ inverse
✅ Answer: 2️⃣ non-zero
🔵 Q40. If A is orthogonal ⇒ det(A) = ?
1️⃣ 1
2️⃣ −1
3️⃣ ±1
4️⃣ 0
✅ Answer: 3️⃣ ±1
⚡ Q41–50: JEE Advanced Level
🔵 Q41. Evaluate |1 x x²; 1 y y²; 1 z z²| for x=1, y=2, z=3.
1️⃣ 2
2️⃣ 1
3️⃣ 4
4️⃣ 0
✅ Answer: 3️⃣ 4
🔵 Q42. For A = [[1,2,3],[0,1,4],[5,6,0]], find det(A).
1️⃣ 1
2️⃣ −1
3️⃣ 5
4️⃣ −5
✅ Answer: 4️⃣ −5
🔵 Q43. If det(A)=3, det(B)=4, det(C)=2, then det(ABC) = ?
1️⃣ 24
2️⃣ 9
3️⃣ 12
4️⃣ 8
✅ Answer: 1️⃣ 24
🔵 Q44. If det(A)=2, find det(2A adj A) (3×3).
1️⃣ 64
2️⃣ 128
3️⃣ 256
4️⃣ 512
✅ Answer: 2️⃣ 128
🔵 Q45. If A symmetric, B skew-symmetric ⇒ det(A+B) = det(A−B)?
1️⃣ True
2️⃣ False
3️⃣ Only for even order
4️⃣ None
✅ Answer: 1️⃣ True
🔵 Q46. A adj A = (det A) I ⇒ det(adj A) = ? (n=3)
1️⃣ (det A)²
2️⃣ (det A)³
3️⃣ (det A)⁴
4️⃣ det A
✅ Answer: 1️⃣
🔵 Q47. Solve for x:| x 1 1 | | 1 x 1 | | 1 1 x | = 0
1️⃣ x = 0
2️⃣ x = 1
3️⃣ x = 2
4️⃣ x = −2
✅ Answer: 2️⃣ x = 1
🔵 Q48. If determinant = 0 ⇒ system is
1️⃣ consistent unique
2️⃣ inconsistent or infinite solutions
3️⃣ inconsistent only
4️⃣ unique only
✅ Answer: 2️⃣
🔵 Q49. If det(A) = −2, find det(adj A × A⁻¹).
1️⃣ 1
2️⃣ −1
3️⃣ 2
4️⃣ −2
✅ Answer: 1️⃣ 1
🔵 Q50. |1 a a²; 1 b b²; 1 c c²| = 0 ⇒ a, b, c are
1️⃣ equal
2️⃣ in A.P.
3️⃣ in G.P.
4️⃣ in H.P.
✅ Answer: 2️⃣ in A.P.
————————————————————————————————————————————————————————————————————————————
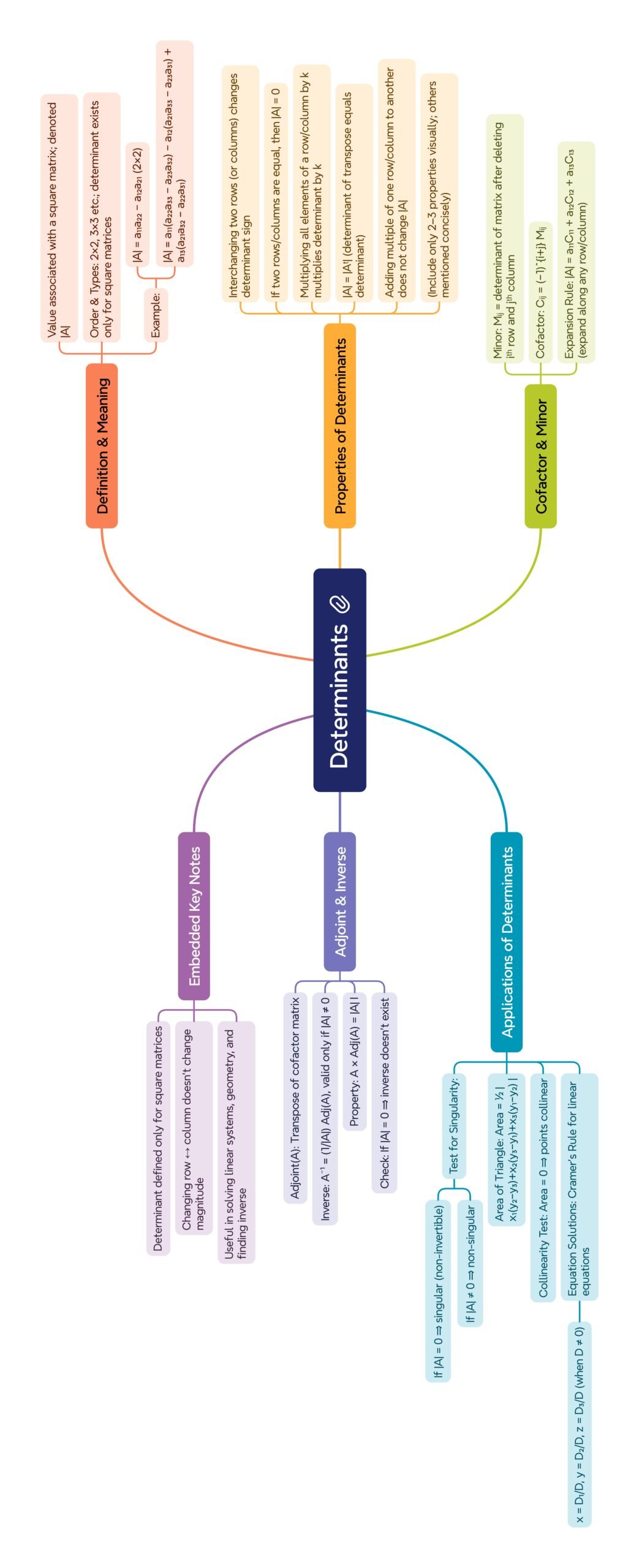
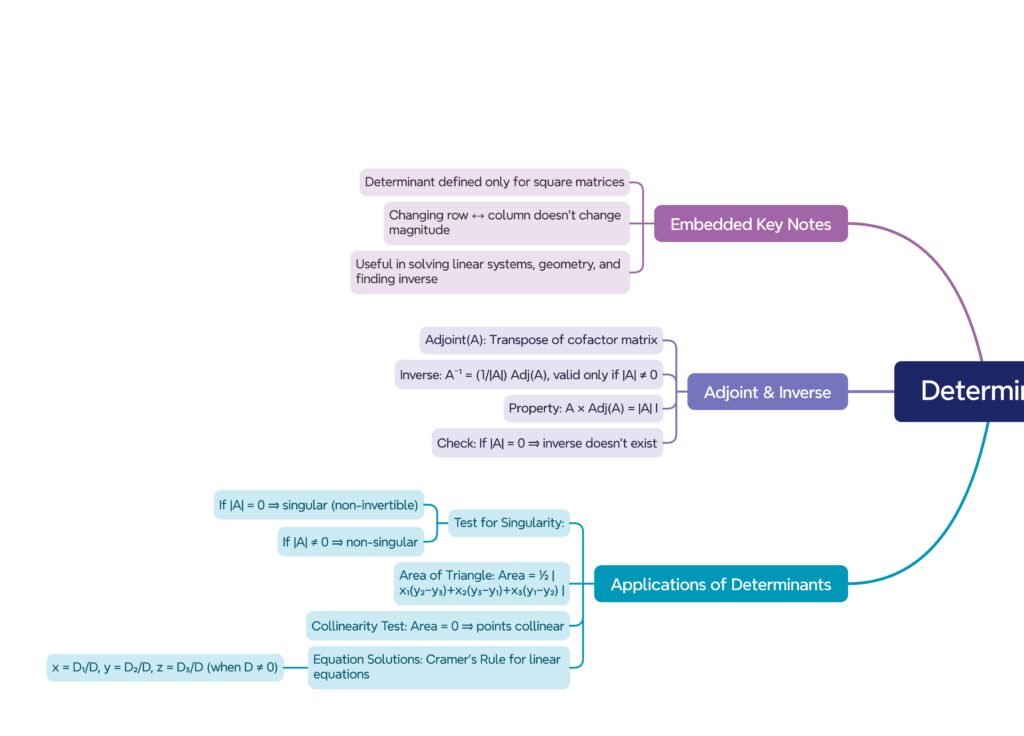
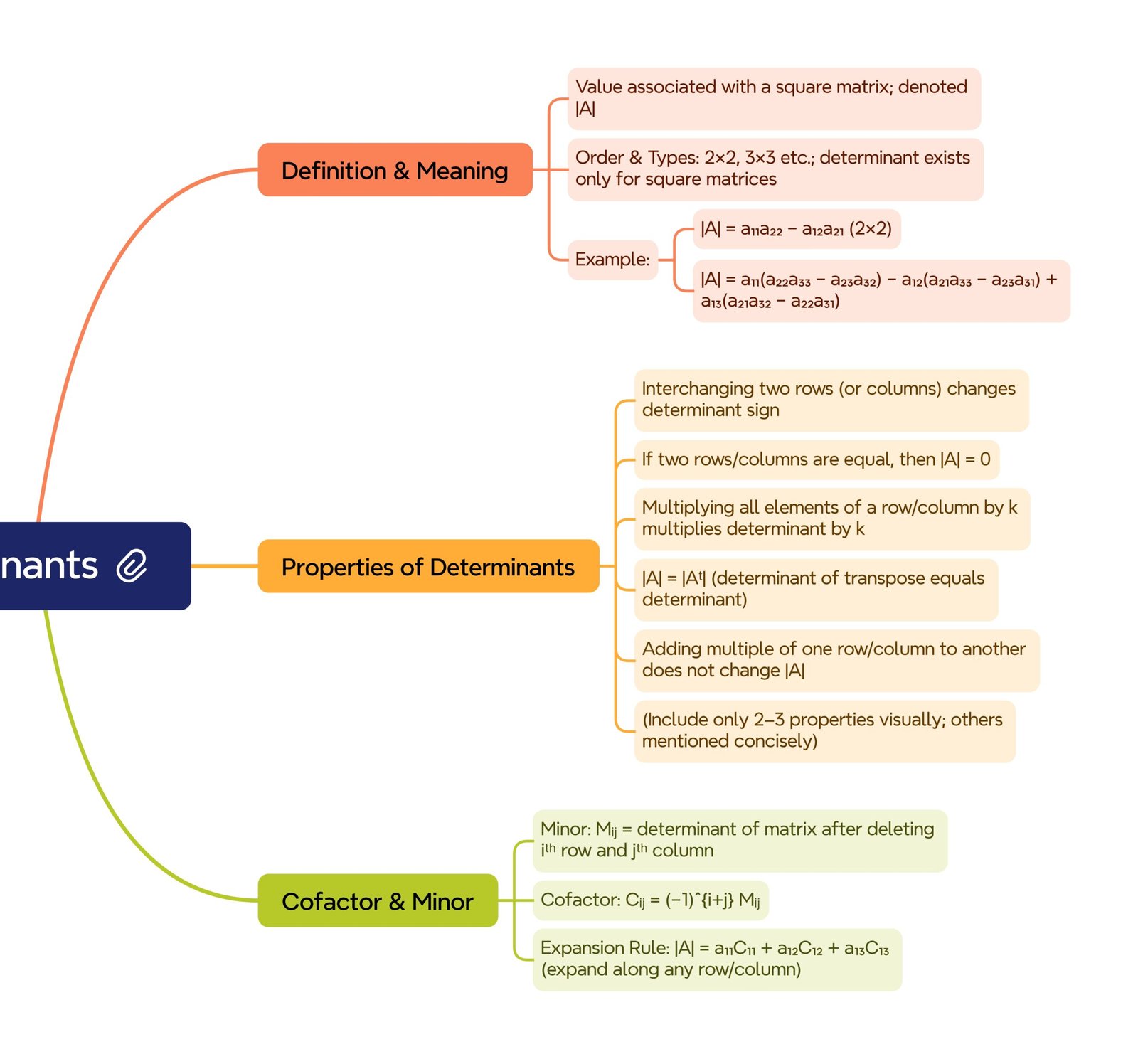
MIND MAPS
————————————————————————————————————————————————————————————————————————————
