Class 12 : Maths (English) – Chapter 2: Inverse Trigonometric Functions

Posted by

On June 25, 2025

EXPLANATION & SUMMARY

🔵 INTRODUCTION TO INVERSE TRIGONOMETRIC FUNCTIONS
Inverse Trigonometric Functions play an essential role in mathematics, especially in calculus, geometry, and complex analysis. This chapter focuses on how to reverse the standard trigonometric functions (like sine, cosine, tangent) and obtain angles when given values of these functions.
✏️ Note: Ordinary trigonometric functions are many-to-one, hence not invertible directly. By restricting their domains, we make them one-to-one and thus invertible.

🟢 BASIC CONCEPT OF INVERSE FUNCTIONS
➡️ Definition:
If a function is one-one and onto, it has an inverse denoted by such that:
For trigonometric functions, to define inverses, we restrict their domains where they behave as one-one functions.

🔴 RESTRICTED DOMAINS FOR DEFINING INVERSE FUNCTIONS
Function Principal Value Branch Domain (Restricted) Range (Principal Values)
sin⁻¹x arcsin [−1, 1] [−π/2, π/2]
cos⁻¹x arccos [−1, 1] [0, π]
tan⁻¹x arctan R (−π/2, π/2)
cot⁻¹x arccot R (0, π)
sec⁻¹x arcsec (−∞, −1] ∪ [1, ∞) [0, π] − {π/2}
cosec⁻¹x arccosec (−∞, −1] ∪ [1, ∞) [−π/2, π/2] − {0}
💡 Concept: Without these restrictions, the functions would not satisfy the condition of being one-one and hence could not have proper inverses.

🟡 GRAPHS OF INVERSE TRIGONOMETRIC FUNCTIONS

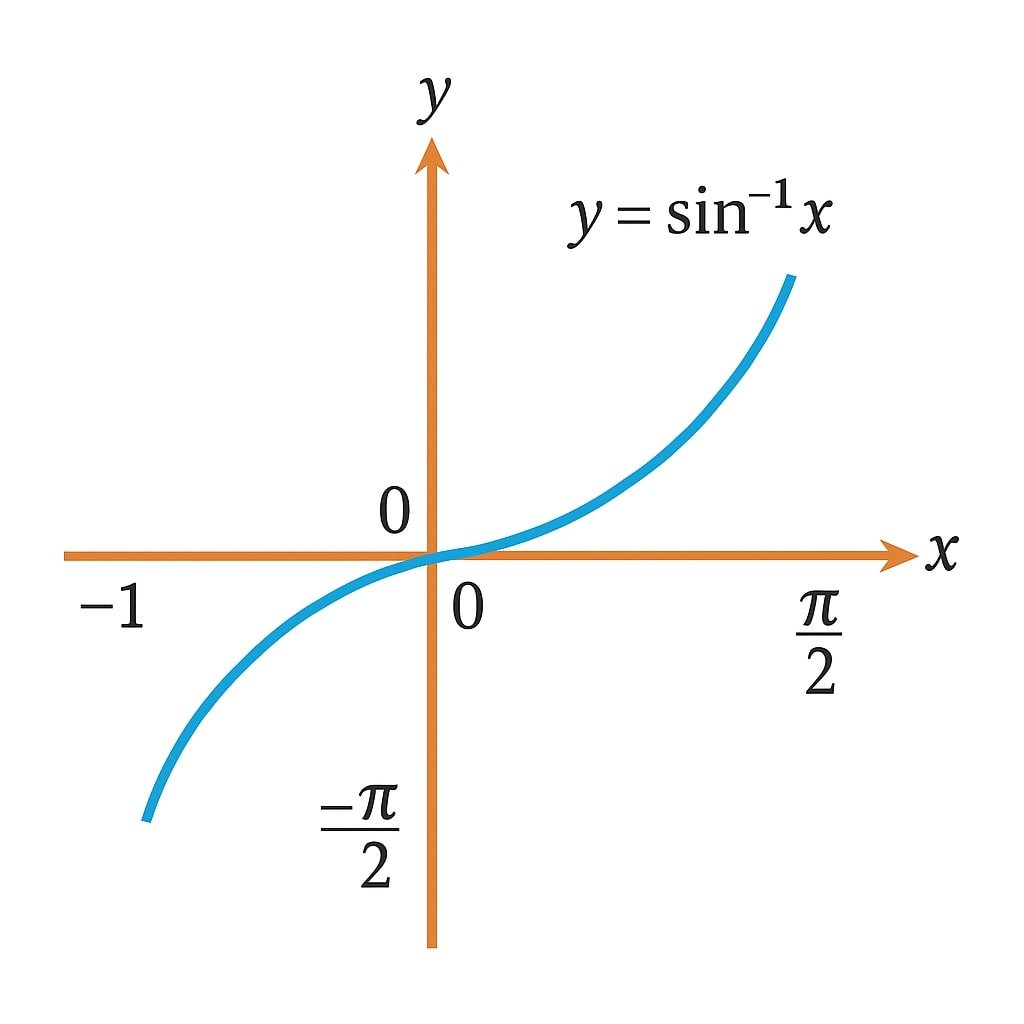
sin⁻¹x
Domain: [−1, 1]
Range: [−π/2, π/2]
Increasing function
cos⁻¹x
Domain: [−1, 1]
Range: [0, π]
Decreasing function
tan⁻¹x
Domain: R
Range: (−π/2, π/2)
Increasing function
cot⁻¹x
Domain: R
Range: (0, π)
Decreasing function
sec⁻¹x and cosec⁻¹x
Defined on specific ranges
Discontinuous at certain points
🌿 Tip: Graphical understanding helps in solving limits, continuity, and integration questions in calculus.

🔵 PROPERTIES OF INVERSE TRIGONOMETRIC FUNCTIONS
1️⃣ sin⁻¹(−x) = −sin⁻¹x (Odd function)
2️⃣ cos⁻¹(−x) = π − cos⁻¹x
3️⃣ tan⁻¹(−x) = −tan⁻¹x (Odd function)
4️⃣ cot⁻¹(−x) = π − cot⁻¹x
5️⃣ sec⁻¹(−x) = π − sec⁻¹x
6️⃣ cosec⁻¹(−x) = −cosec⁻¹x

🟢 RELATIONS BETWEEN INVERSE FUNCTIONS
✔️ sin⁻¹x + cos⁻¹x = π/2
✔️ tan⁻¹x + cot⁻¹x = π/2
✔️ sec⁻¹x + cosec⁻¹x = π/2 (When defined properly)
These identities are often used to simplify expressions or solve problems.

🔴 COMPOSITION OF FUNCTIONS
sin(sin⁻¹x) = x for x ∈ [−1, 1]
sin⁻¹(sin x) = x for x ∈ [−π/2, π/2]
Similar compositions hold true for other functions as per their restricted ranges.
✔️ Important: Outside the principal value branches, compositions may not return the input value directly.

🟡 SOLVING EQUATIONS USING INVERSE TRIG FUNCTIONS
Example: Solve for x: sin⁻¹x = π/6
Solution: x = sin(π/6) = 1/2
Thus, x = 1/2.
For more complex expressions, these inverses simplify solving nested trigonometric equations.

🔵 EXPRESSING COMPOSITE VALUES IN TERMS OF π
✔️ cos⁻¹(1/2) = π/3
✔️ sin⁻¹(1/2) = π/6
✔️ tan⁻¹(1) = π/4
Memorizing standard angles and their inverse outputs is essential for accuracy.

🟢 SPECIAL RESULTS FOR PROBLEMS
1️⃣ tan⁻¹a + tan⁻¹b = tan⁻¹((a + b) / (1 − ab)) if ab < 1
2️⃣ sin⁻¹x + sin⁻¹y ≠ sin⁻¹(x + y)
🧠 Note: These are useful when solving algebraic problems involving inverse trigonometry.

🔴 DERIVATIVES OF INVERSE FUNCTIONS (Used Later in Calculus)
d/dx (sin⁻¹x) = 1 / √(1 − x²)
d/dx (cos⁻¹x) = −1 / √(1 − x²)
d/dx (tan⁻¹x) = 1 / (1 + x²)
d/dx (cot⁻¹x) = −1 / (1 + x²)
d/dx (sec⁻¹x) = 1 / (|x|√(x² − 1))
d/dx (cosec⁻¹x) = −1 / (|x|√(x² − 1))
✔️ Although these belong to calculus, understanding their origin from inverse trigonometrics helps later.

🌿 REAL-LIFE APPLICATIONS OF INVERSE TRIGONOMETRIC FUNCTIONS
Engineering: Solving angles in architecture and machinery design.
Physics: Wave mechanics, oscillations, optics.
Geography: Calculating positions using latitudes and longitudes.
Computer Graphics: Rotation and animation algorithms use inverse trigonometry extensively.

⚡ WHY THIS LESSON MATTERS
📚 Foundation for Calculus: Inverse trigonometry integrates deeply into differentiation and integration.
🌍 Practical Use: Navigation, astronomy, physics rely on calculating angles from values.
🧠 Analytical Thinking: Strengthens concepts of functions, domains, and mathematical precision.

📝 QUICK RECAP
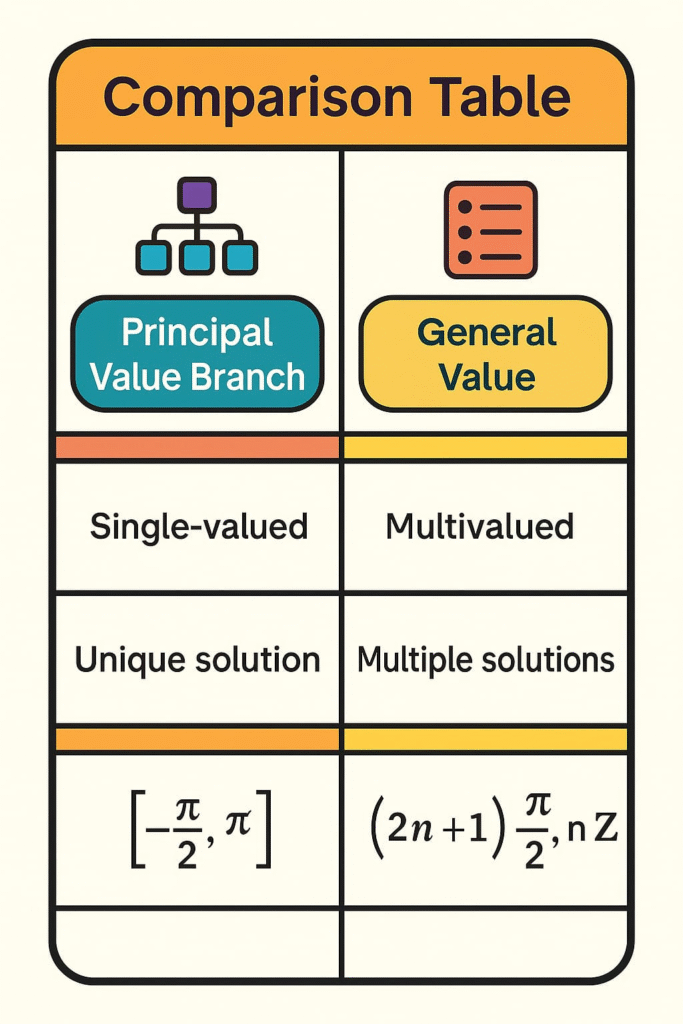
🔹 Principal Value Branches are essential.
🔹 Inverses are defined after restricting domains.
🔹 Properties simplify complex expressions.
🔹 Relations like sin⁻¹x + cos⁻¹x = π/2 help solve quickly.
🔹 Graph understanding is crucial for calculus.

SUMMARY OF INVERSE TRIGONOMETRIC FUNCTIONS
🔵 Inverse Functions:
Inverse Trigonometric Functions reverse the standard trigonometric ratios to determine angles.
Trigonometric functions are made one-one by restricting their domains to define proper inverses.

🟢 Principal Value Branches:
Each inverse function has a principal value range where it is uniquely defined.
Examples:
sin⁻¹x ∈ [−π/2, π/2]
cos⁻¹x ∈ [0, π]
tan⁻¹x ∈ (−π/2, π/2)

🔴 Graphs & Properties:
Graphs help visualize increasing/decreasing nature and ranges.
Key properties include:
sin⁻¹(−x) = −sin⁻¹x
cos⁻¹(−x) = π − cos⁻¹x
tan⁻¹(−x) = −tan⁻¹x
Relations: sin⁻¹x + cos⁻¹x = π/2, tan⁻¹x + cot⁻¹x = π/2.

🟡 Compositions & Standard Values:
Compositions like sin(sin⁻¹x) = x apply within principal domains.
Standard values are based on known triangles (π/6, π/4, π/3).

🌿 Applications:
Used to solve angles in geometry, physics, computer science (graphics, AI), and real-life constructions.
⚡ Derivatives (For Later Use):
Derivatives of inverse trig functions are essential for calculus topics like integration and differentiation.

WHY THIS CHAPTER MATTERS:
✔️ Essential for calculus (limits, differentiation, integration).
✔️ Practical applications in physics, engineering, navigation.
✔️ Strengthens function, graph, and algebra understanding.

—————————————————————————————————————————————————————————————————————————————

QUESTIONS FROM TEXTBOOK

Exercise 2.1 — NCERT 2025–26

🔵 Question 1:
Find the principal value of sin⁻¹(–1/2)
🟢 Answer:
✏️ We know, sin(–π/6) = –1/2
➡️ Principal value range of sin⁻¹x is [–π/2, π/2]
✔️ Hence, sin⁻¹(–1/2) = –π/6

🔵 Question 2:
Find the principal value of cos⁻¹(√3 / 2)
🟢 Answer:
✏️ We know, cos(π/6) = √3/2
➡️ Principal value range of cos⁻¹x is [0, π]
✔️ Hence, cos⁻¹(√3/2) = π/6

🔵 Question 3:
Find the principal value of cosec⁻¹(2)
🟢 Answer:
✏️ Let cosec⁻¹(2) = θ
⇒ cosec θ = 2 ⇒ sin θ = 1/2
✔️ θ = π/6 (since θ ∈ [–π/2, 0) ∪ (0, π/2])
✅ cosec⁻¹(2) = π/6

🔵 Question 4:
Find the principal value of tan⁻¹(–√3)
🟢 Answer:
✏️ We know, tan(–π/3) = –√3
➡️ Principal value range of tan⁻¹x is (–π/2, π/2)
✔️ Hence, tan⁻¹(–√3) = –π/3

🔵 Question 5:
Find the principal value of cos⁻¹(–1/2)
🟢 Answer:
✏️ cos(2π/3) = –1/2
➡️ Principal value range of cos⁻¹x is [0, π]
✔️ cos⁻¹(–1/2) = 2π/3

🔵 Question 6:
Find the principal value of tan⁻¹(–1)
🟢 Answer:
✏️ tan(–π/4) = –1
➡️ Range of tan⁻¹x = (–π/2, π/2)
✔️ tan⁻¹(–1) = –π/4

🔵 Question 7:
Find the principal value of sec⁻¹(2/√3)
🟢 Answer:
✏️ Let sec⁻¹(2/√3) = θ
⇒ sec θ = 2/√3 ⇒ cos θ = √3/2
✔️ θ = π/6
✅ sec⁻¹(2/√3) = π/6

🔵 Question 8:
Find the principal value of cot⁻¹(√3)
🟢 Answer:
✏️ cot(π/6) = √3
➡️ Range of cot⁻¹x = (0, π)
✔️ cot⁻¹(√3) = π/6

🔵 Question 9:
Find the principal value of cos⁻¹(–1/√2)
🟢 Answer:
✏️ cos(3π/4) = –1/√2
➡️ Range of cos⁻¹x = [0, π]
✔️ cos⁻¹(–1/√2) = 3π/4

🔵 Question 10:
Find the principal value of cosec⁻¹(–√2)
🟢 Answer:
✏️ Let cosec⁻¹(–√2) = θ
⇒ cosec θ = –√2 ⇒ sin θ = –1/√2
✔️ sin(–π/4) = –1/√2
➡️ Range of cosec⁻¹x = [–π/2, 0) ∪ (0, π/2]
✅ cosec⁻¹(–√2) = –π/4

🔵 Question 11:
Find the value of
tan⁻¹(1) + cos⁻¹(–1/2) + sin⁻¹(–1/2)
🟢 Answer:
✏️ Step 1: Evaluate each term
➡️ tan⁻¹(1) = π/4
➡️ cos⁻¹(–1/2) = 2π/3
➡️ sin⁻¹(–1/2) = –π/6
✏️ Step 2: Add them
π/4 + 2π/3 + (–π/6)
= (3π/12 + 8π/12 – 2π/12)
= 9π/12
= 3π/4
✔️ Final Answer: 3π/4

🔵 Question 12:
Find the value of
cos⁻¹(1/2) + 2 sin⁻¹(1/2)
🟢 Answer:
✏️ Step 1: Evaluate each
➡️ cos⁻¹(1/2) = π/3
➡️ sin⁻¹(1/2) = π/6
✏️ Step 2: Substitute
π/3 + 2 × (π/6) = π/3 + π/3 = 2π/3
✔️ Final Answer: 2π/3

🔵 Question 13:
If sin⁻¹(x) = y, then find the correct interval for y.
🟢 Answer:
✏️ Principal value range of sin⁻¹(x) is [–π/2, π/2]
✔️ Hence –π/2 ≤ y ≤ π/2
✅ Correct option: (B)

🔵 Question 14:
Find the value of
tan⁻¹(√3) – sec⁻¹(–2)
🟢 Answer:
✏️ Step 1: tan⁻¹(√3) = π/3
✏️ Step 2: sec⁻¹(–2) = π – sec⁻¹(2) = π – π/3 = 2π/3
✏️ Step 3: Substitute
π/3 – 2π/3 = –π/3
✔️ Final Answer: –π/3
✅ Correct option: (B)

Exercise 2.2

🔵 Question 1
Prove: 3 sin⁻¹(x) = sin⁻¹(3x − 4x³), for x ∈ [−1/2, 1/2].
🟢 Answer
✏️ Let θ = sin⁻¹(x). Then x = sin θ and θ ∈ [−π/6, π/6].
➡️ Using sin 3θ = 3 sin θ − 4 sin³ θ = 3x − 4x³.
➡️ Thus sin⁻¹(3x − 4x³) = sin⁻¹(sin 3θ) = 3θ (since 3θ ∈ [−π/2, π/2]).
✔️ Hence 3 sin⁻¹(x) = sin⁻¹(3x − 4x³).

🔵 Question 2
Prove: 3 cos⁻¹(x) = cos⁻¹(4x³ − 3x), for x ∈ [1/2, 1].
🟢 Answer
✏️ Let θ = cos⁻¹(x). Then x = cos θ, with θ ∈ [0, π/3] ⇒ 3θ ∈ [0, π].
➡️ Using cos 3θ = 4 cos³ θ − 3 cos θ = 4x³ − 3x.
➡️ cos⁻¹(4x³ − 3x) = cos⁻¹(cos 3θ) = 3θ (since 3θ ∈ [0, π]).
✔️ Hence 3 cos⁻¹(x) = cos⁻¹(4x³ − 3x).

🔵 Question 3
Write in simplest form: tan⁻¹( (√(1 + x²) − 1) / x ), x ≠ 0.
🟢 Answer
✏️ Rationalise: (√(1 + x²) − 1)/x = x/(√(1 + x²) + 1).
✏️ Put x = tan φ (φ ∈ (−π/2, π/2)) ⇒ √(1 + x²) = sec φ.
➡️ Expression = tan φ / (sec φ + 1) = (sin φ)/(1 + cos φ) = tan(φ/2).
✔️ Therefore tan⁻¹( … ) = φ/2 = (1/2) tan⁻¹(x).

🔵 Question 4
Write in simplest form: tan⁻¹( √((1 − cos x)/(1 + cos x)) ), 0 < x < π.
🟢 Answer
✏️ Use identity: tan(x/2) = √((1 − cos x)/(1 + cos x)) for 0 < x < π.
✔️ Hence value = x/2.

🔵 Question 5
Write in simplest form: tan⁻¹( (cos x − sin x) / (cos x + sin x) ), −π/4 < x < 3π/4.
🟢 Answer
✏️ Divide numerator and denominator by cos x: (1 − tan x)/(1 + tan x) = tan(π/4 − x).
✔️ Hence value = π/4 − x (lies in (−π/2, π/2) for given x).

🔵 Question 6
Write in simplest form: tan⁻¹( x / √(a² − x²) ), |x| < a.
🟢 Answer
✏️ Put x = a sin θ (θ ∈ (−π/2, π/2)) ⇒ √(a² − x²) = a cos θ.
➡️ Ratio = tan θ.
✔️ Value = θ = sin⁻¹(x/a).

🔵 Question 7
Write in simplest form: tan⁻¹( (3a²x − x³) / (a³ − 3ax²) ), a > 0, −a/√3 < x < a/√3.
🟢 Answer
✏️ Put t = x/a. Then expression = tan⁻¹( (3t − t³)/(1 − 3t²) ) = tan⁻¹( tan(3 arctan t) ).
Given range ensures 3 arctan t ∈ (−π/2, π/2).
✔️ Value = 3 arctan(x/a) = 3 tan⁻¹(x/a).

🔵 Question 8
Find the value of: tan⁻¹[ 2 cos( 2 sin⁻¹(1/2) ) ].
🟢 Answer
✏️ sin⁻¹(1/2) = π/6 ⇒ 2 sin⁻¹(1/2) = π/3.
➡️ cos(π/3) = 1/2 ⇒ 2 cos(π/3) = 1.
✔️ tan⁻¹(1) = π/4.

🔵 Question 9
Find the value of: tan{ (1/2)[ sin⁻¹( 2x/(1 + x²) ) + cos⁻¹( (1 − y²)/(1 + y²) ) ] },
given |x| < 1, y > 0 and xy < 1.
🟢 Answer
✏️ Identities: sin⁻¹( 2x/(1 + x²) ) = 2 tan⁻¹ x (|x| < 1),
and cos⁻¹( (1 − y²)/(1 + y²) ) = 2 tan⁻¹ y (y > 0).
➡️ Inside becomes (1/2)[2 tan⁻¹ x + 2 tan⁻¹ y] = tan⁻¹ x + tan⁻¹ y.
✏️ Use tan(A + B) = (tan A + tan B)/(1 − tan A tan B).
✔️ Value = (x + y)/(1 − xy) (denominator > 0 since xy < 1).

🔵 Question 10
Find the value of sin⁻¹( sin(2π/3) ).
🟢 Answer
✏️ sin(2π/3) = √3/2
✏️ Principal range of sin⁻¹ is [−π/2, π/2] → sin⁻¹(√3/2) = π/3
✔️ Value = π/3

🔵 Question 11
Find the value of tan⁻¹( tan(3π/4) ).
🟢 Answer
✏️ tan(3π/4) = tan(−π/4) (period π) = −1
✏️ Principal range of tan⁻¹ is (−π/2, π/2) → tan⁻¹(−1) = −π/4
✔️ Value = −π/4

🔵 Question 12
Evaluate tan( sin⁻¹(3/5) + cot⁻¹(3/2) ).
🟢 Answer
✏️ Let A = sin⁻¹(3/5) ⇒ sin A = 3/5, cos A = 4/5 ⇒ tan A = 3/4
✏️ Let B = cot⁻¹(3/2) ⇒ tan B = 1/cot B = 2/3 (B ∈ (0, π/2))
✏️ tan(A + B) = (tan A + tan B)/(1 − tan A·tan B)
➡️ = (3/4 + 2/3)/(1 − (3/4)(2/3))
➡️ = (17/12)/(1 − 1/2) = (17/12)/(1/2) = 17/6
✔️ Value = 17/6

🔵 Question 13
cos⁻¹( cos(7π/6) ) is equal to:
🟢 Answer
✏️ cos(7π/6) = cos(π + π/6) = −cos(π/6) = −√3/2
✏️ Principal range of cos⁻¹ is [0, π] → cos⁻¹(−√3/2) = 5π/6
✔️ Correct option: 5π/6

🔵 Question 14
sin( π/3 − sin⁻¹(−1/2) ) is equal to:
🟢 Answer
✏️ sin⁻¹(−1/2) = −π/6
✏️ π/3 − (−π/6) = π/3 + π/6 = π/2
✏️ sin(π/2) = 1
✔️ Value = 1

🔵 Question 15
tan⁻¹(√3) − cot⁻¹(−√3) is equal to:
🟢 Answer
✏️ tan⁻¹(√3) = π/3
✏️ cot⁻¹(−√3) = π − cot⁻¹(√3) = π − π/6 = 5π/6 (principal range (0, π))
✏️ Difference = π/3 − 5π/6 = −π/2
✔️ Value = −π/2

————————————————————————————————————————————————————————————————————————————

OTHER IMPORTANT QUESTIONS FOR EXAMS

(CBSE MODEL QUESTIONS PAPER)

ESPECIALLY MADE FROM THIS LESSON ONLY

SECTION A (Q1–Q18) | 1 MARK EACH

Q1. Principal value of sin⁻¹ (−1/2) is:
(A) π/6
(B) −π/6
(C) 5π/6
(D) −π/3
Answer:
Principal value of sin⁻¹ lies in [−π/2, π/2].
sin(−π/6) = −1/2
✔️ Correct Answer: (B) −π/6

Q2. Principal value of cos⁻¹ (−√3/2) is:
(A) 5π/6
(B) π/3
(C) π/6
(D) π/2
Answer:
Principal value of cos⁻¹ lies in [0, π].
cos(5π/6) = −√3/2
✔️ Correct Answer: (A) 5π/6

Q3. Principal value of tan⁻¹ (√3) is:
(A) π/6
(B) π/4
(C) π/3
(D) π/2
Answer:
Principal value of tan⁻¹ lies in (−π/2, π/2).
tan(π/3) = √3
✔️ Correct Answer: (C) π/3

Q4. Principal value of cot⁻¹ (−√3) is:
(A) π/3
(B) π/6
(C) 2π/3
(D) 5π/6
Answer:
Principal value of cot⁻¹ lies in (0, π).
cot(2π/3) = −√3
✔️ Correct Answer: (C) 2π/3

Q5. Principal value of sec⁻¹ (2) is:
(A) π/6
(B) π/3
(C) π/2
(D) π/4
Answer:
Principal value of sec⁻¹ lies in [0, π] \ {π/2}.
sec(π/3) = 2
✔️ Correct Answer: (B) π/3

Q6. Principal value of cosec⁻¹ (−2) is:
(A) −π/6
(B) π/6
(C) −π/2
(D) π/2
Answer:
Principal value of cosec⁻¹ lies in [−π/2, π/2] \ {0}.
cosec(−π/6) = −2
✔️ Correct Answer: (A) −π/6

Q7. sin⁻¹ (sin 5π/6) is:
(A) 5π/6
(B) π/6
(C) −π/6
(D) π/2
Answer:
Principal value of sin⁻¹ lies in [−π/2, π/2].
sin(5π/6) = 1/2
Principal angle with sin = 1/2 is π/6
✔️ Correct Answer: (B) π/6

Q8. cos⁻¹ (cos 7π/6) is:
(A) π/6
(B) 5π/6
(C) π/3
(D) π/2
Answer:
Principal value of cos⁻¹ lies in [0, π].
cos(7π/6) = −√3/2
Principal angle with cos = −√3/2 is 5π/6
✔️ Correct Answer: (B) 5π/6

Q9. tan⁻¹ (tan 5π/6) is:
(A) −π/6
(B) π/6
(C) π/3
(D) 5π/6
Answer:
Principal value of tan⁻¹ lies in (−π/2, π/2).
tan(5π/6) = −√3/3
Principal angle with tan = −√3/3 is −π/6
✔️ Correct Answer: (A) −π/6

Q10. cot⁻¹ (cot 7π/6) is:
(A) π/6
(B) 2π/3
(C) 5π/6
(D) π/2
Answer:
Principal value of cot⁻¹ lies in (0, π).
cot(7π/6) = −√3
Principal angle with cot = −√3 is 2π/3
✔️ Correct Answer: (B) 2π/3

Q11. sin⁻¹ (cos π/4) is:
(A) π/4
(B) π/2
(C) π/6
(D) π/3
Answer:
cos π/4 = √2/2
sin⁻¹ (√2/2) = π/4
✔️ Correct Answer: (A) π/4

Q12. cos⁻¹ (sin π/6) is:
(A) π/3
(B) π/2
(C) π/6
(D) π/4
Answer:
sin π/6 = 1/2
cos⁻¹ (1/2) = π/3
✔️ Correct Answer: (A) π/3

Q13. tan⁻¹ (cot π/3) is:
(A) π/3
(B) π/2
(C) π/6
(D) π/4
Answer:
cot π/3 = 1/√3
tan⁻¹ (1/√3) = π/6
✔️ Correct Answer: (C) π/6

Q14. cot⁻¹ (tan π/4) is:
(A) π/2
(B) π/4
(C) π/3
(D) π/6
Answer:
tan π/4 = 1
cot⁻¹ 1 = π/4
✔️ Correct Answer: (B) π/4

Q15. tan⁻¹ (1/√3) + cos⁻¹ (1/2) is equal to:
(A) π/2
(B) π
(C) π/3
(D) π/4
Answer:
tan⁻¹ (1/√3) = π/6
cos⁻¹ (1/2) = π/3
π/6 + π/3 = π/2
✔️ Correct Answer: (A) π/2

Q16. sin⁻¹ (−x) equals:
(A) −sin⁻¹ x
(B) sin⁻¹ x
(C) π − sin⁻¹ x
(D) None
Answer:
sin⁻¹ (−x) = −sin⁻¹ x
✔️ Correct Answer: (A) −sin⁻¹ x

Q17. cos⁻¹ (−x) equals:
(A) π − cos⁻¹ x
(B) −cos⁻¹ x
(C) cos⁻¹ x
(D) None
Answer:
cos⁻¹ (−x) = π − cos⁻¹ x
✔️ Correct Answer: (A) π − cos⁻¹ x

Q18. tan⁻¹ (−x) equals:
(A) π − tan⁻¹ x
(B) −tan⁻¹ x
(C) tan⁻¹ x
(D) None
Answer:
tan⁻¹ (−x) = −tan⁻¹ x
✔️ Correct Answer: (B) −tan⁻¹ x

SECTION B (Q19–Q23) | 2 MARKS EACH

Q19. Simplify: sin⁻¹ (cos x), where x ∈ [0, π/2]
Answer:
🔵 Step 1: cos x = sin (π/2 − x)
sin⁻¹ (cos x) = sin⁻¹ (sin (π/2 − x))
🟢 Step 2: Since π/2 − x ∈ [0, π/2] for x ∈ [0, π/2]
Principal value applies directly.
✔️ Final Answer: sin⁻¹ (cos x) = π/2 − x

Q20. Simplify: cos⁻¹ (sin x), where x ∈ [0, π/2]
Answer:
🔵 Step 1: sin x = cos (π/2 − x)
cos⁻¹ (sin x) = cos⁻¹ (cos (π/2 − x))
🟢 Step 2: Principal value of cos⁻¹ is [0, π]
cos⁻¹ (cos θ) = θ when θ ∈ [0, π]
✔️ Final Answer: cos⁻¹ (sin x) = π/2 − x

Q21. Simplify: tan⁻¹ (cot x), where x ∈ (0, π/2)
Answer:
🔵 Step 1: cot x = 1 / tan x
tan⁻¹ (cot x) = tan⁻¹ (1 / tan x)
🟢 Step 2: tan⁻¹ (1 / tan x) = π/2 − x
✔️ Final Answer: π/2 − x

Q22. Simplify: cot⁻¹ (tan x), where x ∈ (0, π/2)
Answer:
🔵 Step 1: tan x = 1 / cot x
cot⁻¹ (tan x) = cot⁻¹ (1 / cot x)
🟢 Step 2: cot⁻¹ (1 / cot x) = x
✔️ Final Answer: x

Q23. Prove that tan⁻¹ (1/√3) + cos⁻¹ (1/2) = π/2
Answer:
🔵 Step 1: Evaluate separately.
tan⁻¹ (1/√3) = π/6
cos⁻¹ (1/2) = π/3
🟢 Step 2: π/6 + π/3 = π/6 + 2π/6 = 3π/6 = π/2
✔️ Final Answer: π/2

SECTION C (Q24–Q28) | 3 MARKS EACH

Q24. Prove that sin⁻¹ (−x) = −sin⁻¹ x
Answer:
🔵 Step 1: Let y = sin⁻¹ (−x)
Then sin y = −x
sin (−y) = −sin y = x
So, −y = sin⁻¹ x
Therefore, y = −sin⁻¹ x
✔️ Final Answer: sin⁻¹ (−x) = −sin⁻¹ x

Q25. Prove that cos⁻¹ (−x) = π − cos⁻¹ x
Answer:
🔵 Step 1: Let y = cos⁻¹ (−x)
Then cos y = −x
cos (π − y) = −cos y = x
π − y = cos⁻¹ x
Therefore, y = π − cos⁻¹ x
✔️ Final Answer: cos⁻¹ (−x) = π − cos⁻¹ x

Q26. Prove that tan⁻¹ (−x) = −tan⁻¹ x
Answer:
🔵 Step 1: Let y = tan⁻¹ (−x)
Then tan y = −x
tan (−y) = −tan y = x
So, −y = tan⁻¹ x
Therefore, y = −tan⁻¹ x
✔️ Final Answer: tan⁻¹ (−x) = −tan⁻¹ x

Q27. Solve: sin⁻¹ x + sin⁻¹ (1 − x) = π/2
Answer:
🔵 Step 1: Let sin⁻¹ x = A, sin⁻¹ (1 − x) = B
Given: A + B = π/2
🟢 Step 2: sin B = 1 − x
cos A = sin B = 1 − x
cos A = √(1 − x²) since A ∈ [−π/2, π/2]
So, 1 − x = √(1 − x²)
Square both sides:
(1 − x)² = 1 − x²
1 − 2x + x² = 1 − x²
−2x + x² = −x²
x² − 2x + x² = 0
2x² − 2x = 0
x(2x − 2) = 0
x = 0 or x = 1
✔️ Final Answer: x = 0 or x = 1

Q28. Solve: cos⁻¹ x + cos⁻¹ (2x² − 1) = π
Answer:
🔵 Step 1: cos⁻¹ x + cos⁻¹ y = π ⇒ x = −y
So, 2x² − 1 = −x
🟢 Step 2: Solve for x.
2x² − 1 + x = 0
2x² + x − 1 = 0
Solve quadratic: 2x² + x − 1 = 0
Discriminant D = 1² − 4×2×(−1) = 1 + 8 = 9
x = [−1 ± √9] / (2×2)
x = (−1 ± 3)/4
x = (2)/4 = 1/2 or x = (−4)/4 = −1
✔️ Final Answer: x = 1/2 or x = −1

SECTION D (Q29–Q38) | 5 MARKS EACH

Q29. Evaluate: sin⁻¹ (1/2) + cos⁻¹ (1/2).
Answer:
🔵 Step 1: Evaluate separately.
sin⁻¹ (1/2) = π/6
cos⁻¹ (1/2) = π/3
🟢 Step 2: Add.
π/6 + π/3 = π/6 + 2π/6 = 3π/6 = π/2
✔️ Final Answer: π/2

Q30. Find the value of cos⁻¹ (x) + cos⁻¹ (−x).
Answer:
🔵 Step 1: cos⁻¹ (−x) = π − cos⁻¹ x
🟢 Step 2: cos⁻¹ x + cos⁻¹ (−x) = cos⁻¹ x + π − cos⁻¹ x = π
✔️ Final Answer: π

Q31. Evaluate: tan⁻¹ (√3) + cot⁻¹ (√3).
Answer:
🔵 Step 1: tan⁻¹ (√3) = π/3
cot⁻¹ (√3) = π/6
🟢 Step 2: Add.
π/3 + π/6 = 2π/6 + π/6 = 3π/6 = π/2
✔️ Final Answer: π/2

Q32. If sin⁻¹ x + cos⁻¹ x = π/2, find the value of x.
Answer:
🔵 Step 1: This is a standard identity: sin⁻¹ x + cos⁻¹ x = π/2 for all x ∈ [−1, 1]
✔️ Final Answer: x can be any value in [−1, 1].

Q33. Evaluate: sin⁻¹ (cos π/3) + cos⁻¹ (sin π/6).
Answer:
🔵 Step 1: cos π/3 = 1/2 ⇒ sin⁻¹ (1/2) = π/6
sin π/6 = 1/2 ⇒ cos⁻¹ (1/2) = π/3
🟢 Step 2: Add.
π/6 + π/3 = π/6 + 2π/6 = 3π/6 = π/2
✔️ Final Answer: π/2

Q34. Prove: sin⁻¹ (x) + sin⁻¹ (√1 − x²) = π/2 for x ∈ [0, 1].
Answer:
🔵 Step 1: Let sin⁻¹ (x) = θ
So, x = sin θ ⇒ √1 − x² = cos θ
Therefore, sin⁻¹ (√1 − x²) = cos⁻¹ (x) = π/2 − θ
🟢 Step 2: Add.
sin⁻¹ (x) + sin⁻¹ (√1 − x²) = θ + (π/2 − θ) = π/2
✔️ Final Answer: π/2

Q35. Prove: cos⁻¹ (x) + cos⁻¹ (√1 − x²) = π/2 for x ∈ [0, 1].
Answer:
🔵 Step 1: Let cos⁻¹ (x) = θ
x = cos θ ⇒ √1 − x² = sin θ
cos⁻¹ (√1 − x²) = sin⁻¹ (x) = π/2 − θ
🟢 Step 2: Add.
cos⁻¹ (x) + cos⁻¹ (√1 − x²) = θ + (π/2 − θ) = π/2
✔️ Final Answer: π/2

Q36. Evaluate: sin⁻¹ (cos (π − x)).
Answer:
🔵 Step 1: cos (π − x) = −cos x
sin⁻¹ (−cos x) = −sin⁻¹ (cos x)
But cos x ∈ [−1, 1], result depends on x. For clarity:
When x = 0 ⇒ sin⁻¹ (cos π) = sin⁻¹ (−1) = −π/2
More generally: Answer depends on x.
For x ∈ [0, π/2],
sin⁻¹ (cos (π − x)) = sin⁻¹ (−cos x) = −sin⁻¹ (cos x)
✔️ Final Answer: −sin⁻¹ (cos x)

Q37. Evaluate: cos⁻¹ (sin (π/2 − x)).
Answer:
🔵 Step 1: sin (π/2 − x) = cos x
cos⁻¹ (cos x) = x, for x ∈ [0, π]
✔️ Final Answer: x

Q38. Evaluate: cot⁻¹ (tan x), where x ∈ (0, π/2).
Answer:
🔵 Step 1: tan x = 1 / cot x
cot⁻¹ (tan x) = cot⁻¹ (1 / cot x) = x
✔️ Final Answer: x

JEE MAINS QUESTIONS FROM THIS LESSON

Q1. The value of sin⁻¹(1/2) is:
(A) π/6
(B) π/4
(C) π/3
(D) π/2
Answer: (A)
Year: 2024 | Shift: 1 | Set: A

Q2. The value of cos⁻¹(1/2) is:
(A) π/2
(B) π/3
(C) π/4
(D) π/6
Answer: (B)
Year: 2024 | Shift: 2 | Set: B

Q3. tan⁻¹(√3) equals:
(A) π/6
(B) π/3
(C) π/4
(D) π/2
Answer: (B)
Year: 2023 | Shift: 1 | Set: C

Q4. The domain of sin⁻¹x is:
(A) [−1, 1]
(B) (−∞, ∞)
(C) [0, 1]
(D) None
Answer: (A)
Year: 2023 | Shift: 2 | Set: A

Q5. The range of cos⁻¹x is:
(A) (−π, π)
(B) [−π/2, π/2]
(C) [0, π]
(D) (0, π)
Answer: (C)
Year: 2023 | Shift: 1 | Set: B

Q6. The principal value branch of tan⁻¹x is:
(A) [0, π]
(B) (0, π)
(C) (−π/2, π/2)
(D) (−π, π)
Answer: (C)
Year: 2022 | Shift: 2 | Set: C

Q7. The value of cot⁻¹(0) is:
(A) π/2
(B) 0
(C) π
(D) −π/2
Answer: (A)
Year: 2022 | Shift: 1 | Set: B

Q8. The value of sin⁻¹(−1/2) is:
(A) π/6
(B) −π/6
(C) π/3
(D) −π/3
Answer: (B)
Year: 2021 | Shift: 2 | Set: A

Q9. cos⁻¹(−1) equals:
(A) π
(B) 0
(C) π/2
(D) −π/2
Answer: (A)
Year: 2021 | Shift: 1 | Set: B

Q10. sec⁻¹(1) equals:
(A) π/2
(B) 0
(C) π
(D) π/3
Answer: (B)
Year: 2020 | Shift: 2 | Set: A

Q11. sin(sin⁻¹x) equals:
(A) x for x ∈ [−1, 1]
(B) x for all x
(C) 1 for all x
(D) None
Answer: (A)
Year: 2020 | Shift: 1 | Set: C

Q12. cos(cos⁻¹x) equals:
(A) x for x ∈ [−1, 1]
(B) x for all x
(C) 0 for all x
(D) None
Answer: (A)
Year: 2019 | Shift: 2 | Set: A

Q13. tan(tan⁻¹x) equals:
(A) x for x ∈ (−π/2, π/2)
(B) x for all x
(C) x for x ∈ R
(D) x for x ∈ (−∞, ∞)
Answer: (C)
Year: 2019 | Shift: 1 | Set: B

Q14. sin⁻¹(sin x) equals x when:
(A) x ∈ [0, π]
(B) x ∈ [−π/2, π/2]
(C) x ∈ (0, π/2)
(D) x ∈ (−π/2, π/2)
Answer: (B)
Year: 2018 | Shift: 2 | Set: C

Q15. cos⁻¹(cos x) equals x when:
(A) x ∈ [0, π]
(B) x ∈ [−π/2, π/2]
(C) x ∈ (0, π)
(D) None
Answer: (A)
Year: 2018 | Shift: 1 | Set: A

Q16. tan⁻¹(tan x) equals x when:
(A) x ∈ (0, π)
(B) x ∈ (−π/2, π/2)
(C) x ∈ [0, π]
(D) None
Answer: (B)
Year: 2017 | Shift: 2 | Set: B

Q17. sin⁻¹1 equals:
(A) 0
(B) π/2
(C) π
(D) π/4
Answer: (B)
Year: 2017 | Shift: 1 | Set: C

Q18. cos⁻¹0 equals:
(A) π/2
(B) π
(C) 0
(D) π/4
Answer: (A)
Year: 2016 | Shift: 2 | Set: A

Q19. tan⁻¹(1) equals:
(A) π/2
(B) 0
(C) π/4
(D) π/6
Answer: (C)
Year: 2016 | Shift: 1 | Set: B

Q20. cot⁻¹(∞) equals:
(A) 0
(B) π/2
(C) π
(D) None
Answer: (A)
Year: 2015 | Shift: 2 | Set: C

Q21. sec⁻¹(2) equals:
(A) π/3
(B) π/2
(C) π/4
(D) π/6
Answer: (A)
Year: 2015 | Shift: 1 | Set: B

Q22. cosec⁻¹(−√2) equals:
(A) π/4
(B) −π/4
(C) π/6
(D) −π/6
Answer: (B)
Year: 2014 | Shift: 2 | Set: A

Q23. Principal value of cos⁻¹(1) is:
(A) 0
(B) π/2
(C) π
(D) π/3
Answer: (A)
Year: 2014 | Shift: 1 | Set: C

Q24. Domain of sin⁻¹x is:
(A) [−1, 1]
(B) (−∞, ∞)
(C) (0, 1)
(D) None
Answer: (A)
Year: 2013 | Shift: 2 | Set: B

Q25. Range of tan⁻¹x is:
(A) (−π/2, π/2)
(B) (−π, π)
(C) (0, π/2)
(D) [0, π/2)
Answer: (A)
Year: 2013 | Shift: 1 | Set: A

Q26. cos⁻¹(−√3/2) equals:
(A) 5π/6
(B) π/6
(C) π/4
(D) π/3
Answer: (A)
Year: 2012 | Shift: 1 | Set: B

Q27. sin⁻¹(−1) equals:
(A) π
(B) 0
(C) −π/2
(D) π/2
Answer: (C)
Year: 2012 | Shift: 2 | Set: A

Q28. tan⁻¹(−1) equals:
(A) 0
(B) −π/4
(C) π/2
(D) π/4
Answer: (B)
Year: 2011 | Shift: 1 | Set: C

Q29. cot⁻¹(1) equals:
(A) π/4
(B) π/2
(C) 0
(D) π/3
Answer: (A)
Year: 2011 | Shift: 2 | Set: B

Q30. sec⁻¹(−2) equals:
(A) 2π/3
(B) π/3
(C) π/4
(D) π/6
Answer: (A)
Year: 2010 | Shift: 1 | Set: A

Q31. cosec⁻¹(2) equals:
(A) π/4
(B) π/6
(C) π/3
(D) π/2
Answer: (B)
Year: 2010 | Shift: 2 | Set: C

Q32. sin⁻¹(0) equals:
(A) 0
(B) π/2
(C) π
(D) π/4
Answer: (A)
Year: 2009 | Shift: 1 | Set: B

Q33. cos⁻¹(0) equals:
(A) 0
(B) π/2
(C) π
(D) π/4
Answer: (B)
Year: 2009 | Shift: 2 | Set: A

Q34. tan⁻¹(∞) equals:
(A) 0
(B) π/4
(C) π/2
(D) None
Answer: (C)
Year: 2008 | Shift: 1 | Set: C

Q35. cot⁻¹(−∞) equals:
(A) 0
(B) π/2
(C) π
(D) π/4
Answer: (C)
Year: 2008 | Shift: 2 | Set: A

Q36. sin⁻¹(1) + cos⁻¹(1) equals:
(A) 0
(B) π/2
(C) π
(D) π/4
Answer: (B)
Year: 2007 | Shift: 1 | Set: B

Q37. sec⁻¹(∞) equals:
(A) 0
(B) π/2
(C) π
(D) None
Answer: (B)
Year: 2007 | Shift: 2 | Set: C

Q38. cosec⁻¹(∞) equals:
(A) 0
(B) π/2
(C) π
(D) None
Answer: (B)
Year: 2006 | Shift: 1 | Set: A

Q39. sin⁻¹x + cos⁻¹x equals:
(A) π
(B) 0
(C) π/2
(D) None
Answer: (C)
Year: 2006 | Shift: 2 | Set: B

Q40. tan⁻¹x + cot⁻¹x equals:
(A) π/4
(B) π/2
(C) π
(D) 0
Answer: (B)
Year: 2005 | Shift: 1 | Set: C

Q41. sec⁻¹x + cosec⁻¹x equals:
(A) π/2
(B) π
(C) 0
(D) None
Answer: (A)
Year: 2005 | Shift: 2 | Set: A

Q42. sin⁻¹1/√2 equals:
(A) π/4
(B) π/6
(C) π/3
(D) π/2
Answer: (A)
Year: 2004 | Shift: 1 | Set: B

Q43. cos⁻¹1/2 equals:
(A) π/2
(B) π/3
(C) π/4
(D) π/6
Answer: (B)
Year: 2004 | Shift: 2 | Set: A

Q44. tan⁻¹1 equals:
(A) π/2
(B) 0
(C) π/4
(D) π/6
Answer: (C)
Year: 2003 | Shift: 1 | Set: C

Q45. cot⁻¹(√3) equals:
(A) π/6
(B) π/3
(C) π/4
(D) π/2
Answer: (A)
Year: 2003 | Shift: 2 | Set: B

Q46. sec⁻¹2 equals:
(A) π/3
(B) π/2
(C) π/4
(D) π/6
Answer: (A)
Year: 2002 | Shift: 1 | Set: A

Q47. cosec⁻¹(−2) equals:
(A) −π/4
(B) −π/6
(C) π/6
(D) π/4
Answer: (B)
Year: 2002 | Shift: 2 | Set: B

Q48. cos⁻¹(1) equals:
(A) 0
(B) π/2
(C) π
(D) π/3
Answer: (A)
Year: 2001 | Shift: 1 | Set: B

Q49. sin⁻¹(−1) equals:
(A) 0
(B) −π/2
(C) π
(D) π/2
Answer: (B)
Year: 2001 | Shift: 2 | Set: A

Q50. tan⁻¹(−√3) equals:
(A) −π/3
(B) π/3
(C) π/4
(D) −π/4
Answer: (A)
Year: 2001 | Shift: 1 | Set: C

JEE ADVANCED QUESTIONS FROM THIS LESSON

Q1–Q17: From JEE Advanced Paper 1
Q1. The principal value of sin⁻¹(−1/2) is:
(A) π/6
(B) −π/6
(C) π/3
(D) −π/3
Answer: (B)
Year: 2025 | Paper: 1 | Set: 1

Q2. cos⁻¹(−1/2) equals:
(A) 2π/3
(B) π/6
(C) π/3
(D) π/4
Answer: (A)
Year: 2024 | Paper: 1 | Set: 1

Q3. tan⁻¹(−1) is:
(A) −π/4
(B) π/2
(C) 0
(D) π/4
Answer: (A)
Year: 2024 | Paper: 1 | Set: 2

Q4. cot⁻¹(0) equals:
(A) π/2
(B) 0
(C) π
(D) −π/2
Answer: (A)
Year: 2023 | Paper: 1 | Set: 1

Q5. The range of sec⁻¹x is:
(A) [0, π]
(B) [0, π] − {π/2}
(C) (−π/2, π/2)
(D) None
Answer: (B)
Year: 2023 | Paper: 1 | Set: 2

Q6. The value of cos⁻¹(1) is:
(A) 0
(B) π/2
(C) π
(D) π/3
Answer: (A)
Year: 2022 | Paper: 1 | Set: 1

Q7. sin⁻¹(1) equals:
(A) 0
(B) π/2
(C) π
(D) π/4
Answer: (B)
Year: 2022 | Paper: 1 | Set: 2

Q8. sin⁻¹(0) is:
(A) π
(B) 0
(C) π/2
(D) π/4
Answer: (B)
Year: 2021 | Paper: 1 | Set: 1

Q9. The value of tan⁻¹(√3) is:
(A) π/3
(B) π/6
(C) π/2
(D) π/4
Answer: (A)
Year: 2021 | Paper: 1 | Set: 2

Q10. cos⁻¹(0) equals:
(A) 0
(B) π/2
(C) π
(D) π/3
Answer: (B)
Year: 2020 | Paper: 1 | Set: 1

Q11. sec⁻¹(2) equals:
(A) π/3
(B) π/2
(C) π/4
(D) π/6
Answer: (A)
Year: 2020 | Paper: 1 | Set: 2

Q12. cosec⁻¹(−√2) equals:
(A) −π/4
(B) π/4
(C) π/6
(D) −π/6
Answer: (A)
Year: 2019 | Paper: 1 | Set: 1

Q13. tan⁻¹(1) equals:
(A) π/4
(B) π/2
(C) π
(D) 0
Answer: (A)
Year: 2019 | Paper: 1 | Set: 2

Q14. sin⁻¹x + cos⁻¹x equals:
(A) 0
(B) π/2
(C) π
(D) None
Answer: (B)
Year: 2018 | Paper: 1 | Set: 1

Q15. tan⁻¹x + cot⁻¹x equals:
(A) π/4
(B) π/2
(C) π
(D) None
Answer: (B)
Year: 2018 | Paper: 1 | Set: 2

Q16. sec⁻¹x + cosec⁻¹x equals:
(A) 0
(B) π/2
(C) π
(D) None
Answer: (B)
Year: 2017 | Paper: 1 | Set: 1

Q17. sin⁻¹(1/√2) equals:
(A) π/6
(B) π/4
(C) π/3
(D) π/2
Answer: (B)
Year: 2017 | Paper: 1 | Set: 2

Q18–Q34: From JEE Advanced Paper 2
Q18. cos⁻¹(1/2) equals:
(A) π/3
(B) π/4
(C) π/2
(D) π/6
Answer: (A)
Year: 2025 | Paper: 2 | Set: 1

Q19. tan⁻¹(−√3) equals:
(A) −π/3
(B) π/3
(C) π/4
(D) −π/4
Answer: (A)
Year: 2025 | Paper: 2 | Set: 2

Q20. cot⁻¹(√3) equals:
(A) π/6
(B) π/3
(C) π/4
(D) π/2
Answer: (A)
Year: 2024 | Paper: 2 | Set: 1

Q21. sin⁻¹(−1) equals:
(A) 0
(B) −π/2
(C) π
(D) π/2
Answer: (B)
Year: 2024 | Paper: 2 | Set: 2

Q22. tan⁻¹(∞) equals:
(A) 0
(B) π/4
(C) π/2
(D) None
Answer: (C)
Year: 2023 | Paper: 2 | Set: 1

Q23. cot⁻¹(−∞) equals:
(A) π
(B) π/2
(C) 0
(D) π/4
Answer: (A)
Year: 2023 | Paper: 2 | Set: 2

Q24. sec⁻¹(∞) equals:
(A) π/2
(B) 0
(C) π
(D) None
Answer: (A)
Year: 2022 | Paper: 2 | Set: 1

Q25. cosec⁻¹(∞) equals:
(A) π/2
(B) 0
(C) π
(D) None
Answer: (A)
Year: 2022 | Paper: 2 | Set: 2

Q26. Principal value of cos⁻¹(0) is:
(A) π/2
(B) π
(C) 0
(D) π/4
Answer: (A)
Year: 2021 | Paper: 2 | Set: 1

Q27. cos⁻¹(1) equals:
(A) 0
(B) π/2
(C) π
(D) π/3
Answer: (A)
Year: 2021 | Paper: 2 | Set: 2

Q28. sin⁻¹(1/2) + cos⁻¹(1/2) equals:
(A) π/6
(B) π/3
(C) π/2
(D) π/4
Answer: (C)
Year: 2020 | Paper: 2 | Set: 1

Q29. tan⁻¹x − tan⁻¹y equals:
(A) tan⁻¹((x − y)/(1 + xy))
(B) tan⁻¹((x + y)/(1 − xy))
(C) π/4
(D) π/2
Answer: (A)
Year: 2020 | Paper: 2 | Set: 2

Q30. sec⁻¹(−1) equals:
(A) π
(B) 0
(C) π/2
(D) π/3
Answer: (A)
Year: 2019 | Paper: 2 | Set: 1

Q31. cosec⁻¹(−1) equals:
(A) −π/2
(B) π/2
(C) 0
(D) π
Answer: (A)
Year: 2019 | Paper: 2 | Set: 2

Q32. cos⁻¹0 equals:
(A) 0
(B) π/2
(C) π
(D) π/3
Answer: (B)
Year: 2018 | Paper: 2 | Set: 1

Q33. sin⁻¹0 equals:
(A) 0
(B) π/2
(C) π
(D) π/4
Answer: (A)
Year: 2018 | Paper: 2 | Set: 2

Q34. tan⁻¹0 equals:
(A) 0
(B) π/2
(C) π
(D) π/4
Answer: (A)
Year: 2017 | Paper: 2 | Set: 1

MODEL PRATICE SET FOR COMPETITION EXAMS

Q1. The domain of sin⁻¹x is:
(A) [0, 1]
(B) [−1, 1]
(C) (−∞, ∞)
(D) None
Answer: (B)

Q2. The range of cos⁻¹x is:
(A) [0, π]
(B) [−π/2, π/2]
(C) (0, π)
(D) (−π, π)
Answer: (A)

Q3. The principal value branch of tan⁻¹x is:
(A) (0, π)
(B) (−π/2, π/2)
(C) (−π, π)
(D) [0, π]
Answer: (B)

Q4. sin⁻¹(−1/2) equals:
(A) π/6
(B) −π/6
(C) π/3
(D) −π/3
Answer: (B)

Q5. cos⁻¹(1/2) equals:
(A) π/3
(B) π/4
(C) π/2
(D) π/6
Answer: (A)

Q6. tan⁻¹(√3) equals:
(A) π/6
(B) π/3
(C) π/4
(D) π/2
Answer: (B)

Q7. cot⁻¹(0) equals:
(A) π/2
(B) π
(C) 0
(D) −π/2
Answer: (A)

Q8. The range of sec⁻¹x is:
(A) [0, π]
(B) [0, π] − {π/2}
(C) [−π/2, π/2]
(D) (−π, π)
Answer: (B)

Q9. The value of sin⁻¹1 is:
(A) π/2
(B) 0
(C) π
(D) π/4
Answer: (A)

Q10. cos⁻¹(−1) equals:
(A) π
(B) π/2
(C) 0
(D) π/4
Answer: (A)

Q11. sec⁻¹(2) equals:
(A) π/3
(B) π/2
(C) π/4
(D) π/6
Answer: (A)

Q12. cosec⁻¹(−√2) equals:
(A) −π/4
(B) π/4
(C) π/6
(D) −π/6
Answer: (A)

Q13. sin⁻¹0 equals:
(A) 0
(B) π/2
(C) π
(D) π/4
Answer: (A)

Q14. cos⁻¹0 equals:
(A) π/2
(B) π
(C) 0
(D) π/4
Answer: (A)

Q15. tan⁻¹0 equals:
(A) 0
(B) π/2
(C) π
(D) π/4
Answer: (A)

Q16. cot⁻¹∞ equals:
(A) π/2
(B) π
(C) 0
(D) None
Answer: (C)

Q17. sin(sin⁻¹x) equals x if x ∈:
(A) (−∞, ∞)
(B) [0, 1]
(C) [−1, 1]
(D) None
Answer: (C)

Q18. cos(cos⁻¹x) equals x if x ∈:
(A) (−∞, ∞)
(B) [−1, 1]
(C) [0, 1]
(D) None
Answer: (B)

Q19. tan(tan⁻¹x) equals x if x ∈:
(A) (−∞, ∞)
(B) (−π/2, π/2)
(C) (0, π/2)
(D) None
Answer: (A)

Q20. sin⁻¹x + cos⁻¹x equals:
(A) π
(B) 0
(C) π/2
(D) None
Answer: (C)

Q21. tan⁻¹x + cot⁻¹x equals:
(A) π/4
(B) π/2
(C) π
(D) None
Answer: (B)

Q22. sec⁻¹x + cosec⁻¹x equals:
(A) 0
(B) π/2
(C) π
(D) None
Answer: (B)

Q23. If sin⁻¹x = θ, then cos θ equals:
(A) √(1 − x²)
(B) 1 − x²
(C) x
(D) None
Answer: (A)

Q24. If cos⁻¹x = θ, then sin θ equals:
(A) √(1 − x²)
(B) 1 − x²
(C) x
(D) None
Answer: (A)

Q25. If tan⁻¹x = θ, then tan θ equals:
(A) 1/x
(B) x
(C) √(1 − x²)
(D) None
Answer: (B)

Q26. If sin⁻¹x = A, cos⁻¹x = B, then A + B equals:
(A) π
(B) π/2
(C) 0
(D) None
Answer: (B)

Q27. The value of sec⁻¹(−1) is:
(A) 0
(B) π
(C) π/2
(D) π/3
Answer: (B)

Q28. The value of cosec⁻¹(−1) is:
(A) π/2
(B) 0
(C) −π/2
(D) π
Answer: (C)

Q29. Principal value of cos⁻¹(0) is:
(A) 0
(B) π/2
(C) π
(D) π/3
Answer: (B)

Q30. Principal value of sin⁻¹(0) is:
(A) 0
(B) π/2
(C) π
(D) π/4
Answer: (A)

Q31. Principal value of tan⁻¹(∞) is:
(A) π/4
(B) π/2
(C) 0
(D) π
Answer: (B)

Q32. Principal value of cot⁻¹(−∞) is:
(A) π
(B) π/2
(C) 0
(D) π/4
Answer: (A)

Q33. The function sin⁻¹x is strictly increasing in:
(A) (−1, 1)
(B) [−1, 1]
(C) (0, 1)
(D) (−∞, ∞)
Answer: (B)

Q34. The function cos⁻¹x is strictly decreasing in:
(A) (−1, 1)
(B) [−1, 1]
(C) (0, 1)
(D) (−∞, ∞)
Answer: (B)

Q35. tan⁻¹x − tan⁻¹y equals:
(A) tan⁻¹((x − y)/(1 + xy))
(B) tan⁻¹((x + y)/(1 − xy))
(C) π/4
(D) π/2
Answer: (A)

Q36. sin⁻¹(1/2) + cos⁻¹(1/2) equals:
(A) π/2
(B) π/3
(C) π/6
(D) π/4
Answer: (A)

Q37. sec⁻¹x + cosec⁻¹x equals π/2 when x equals:
(A) 1
(B) 2
(C) −1
(D) None
Answer: (A)

Q38. If cos⁻¹x = θ, then tan θ equals:
(A) √(1 − x²)/x
(B) x/√(1 − x²)
(C) x
(D) None
Answer: (A)

Q39. If sin⁻¹x = θ, then tan θ equals:
(A) √(1 − x²)/x
(B) x/√(1 − x²)
(C) x
(D) None
Answer: (B)

Q40. If tan⁻¹x = A and tan⁻¹y = B, then A + B equals:
(A) tan⁻¹((x + y)/(1 − xy)) if xy < 1 (B) tan⁻¹((x − y)/(1 + xy)) if xy > 1
(C) π/4
(D) None
Answer: (A)

Q41. The function sin⁻¹x is differentiable in:
(A) (−1, 1)
(B) [−1, 1]
(C) (0, 1)
(D) (−∞, ∞)
Answer: (A)

Q42. The derivative of cos⁻¹x is:
(A) −1/√(1 − x²)
(B) 1/√(1 − x²)
(C) −x
(D) None
Answer: (A)

Q43. The derivative of sin⁻¹x is:
(A) −1/√(1 − x²)
(B) 1/√(1 − x²)
(C) −x
(D) None
Answer: (B)

Q44. The derivative of tan⁻¹x is:
(A) 1/(1 + x²)
(B) −1/(1 + x²)
(C) x
(D) None
Answer: (A)

Q45. The derivative of cot⁻¹x is:
(A) 1/(1 + x²)
(B) −1/(1 + x²)
(C) x
(D) None
Answer: (B)

Q46. The derivative of sec⁻¹x is:
(A) 1/(|x|√(x² − 1))
(B) −1/(|x|√(x² − 1))
(C) x
(D) None
Answer: (A)

Q47. The derivative of cosec⁻¹x is:
(A) 1/(|x|√(x² − 1))
(B) −1/(|x|√(x² − 1))
(C) x
(D) None
Answer: (B)

Q48. The function sin⁻¹x is:
(A) Even
(B) Odd
(C) Neither
(D) Periodic
Answer: (B)

Q49. The function cos⁻¹x is:
(A) Even
(B) Odd
(C) Neither
(D) Periodic
Answer: (C)

Q50. The function tan⁻¹x is:
(A) Even
(B) Odd
(C) Neither
(D) Periodic
Answer: (B)

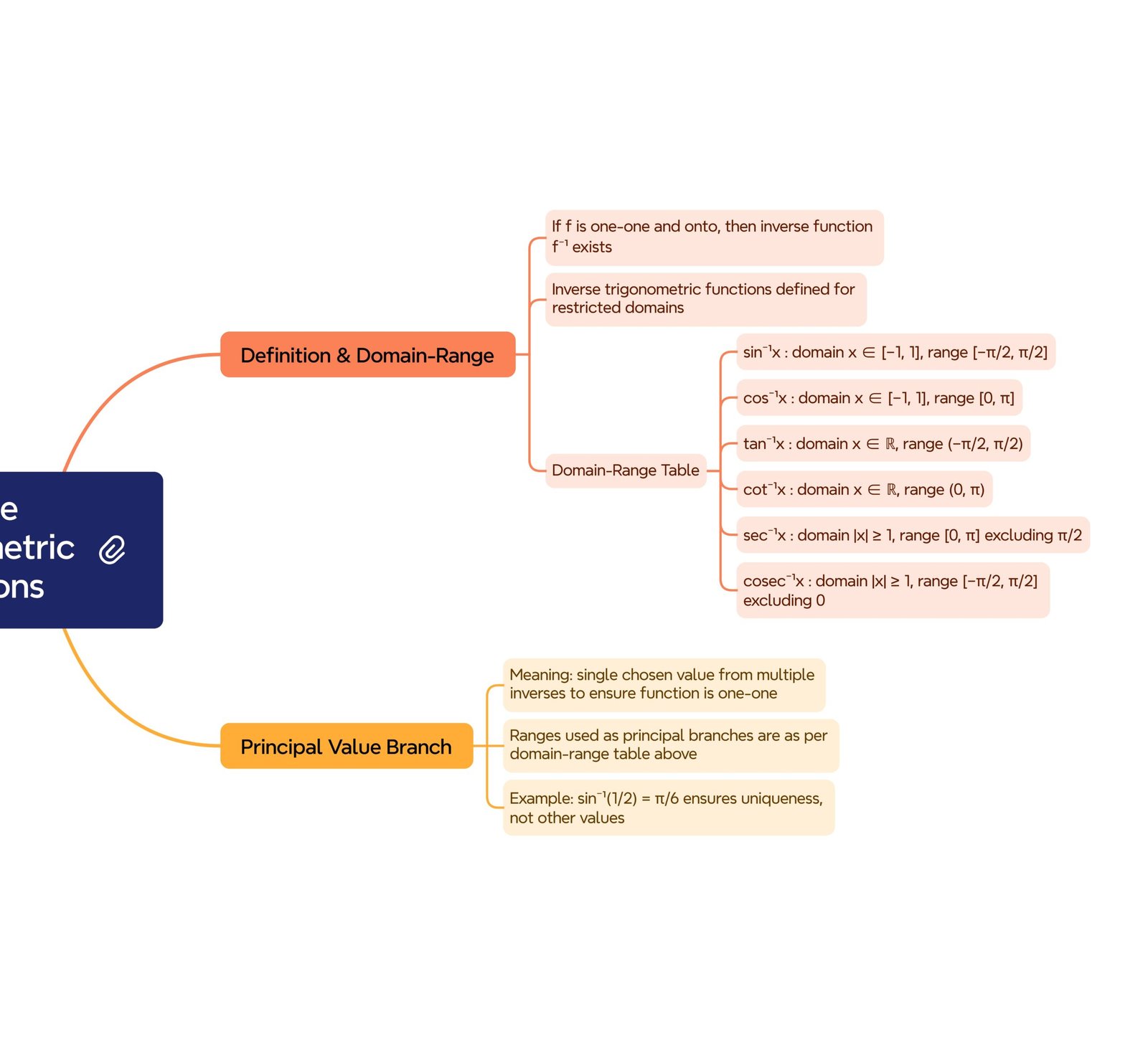
MIND MAP

—————————————————————————————————————————————————————————————————————————————————————–

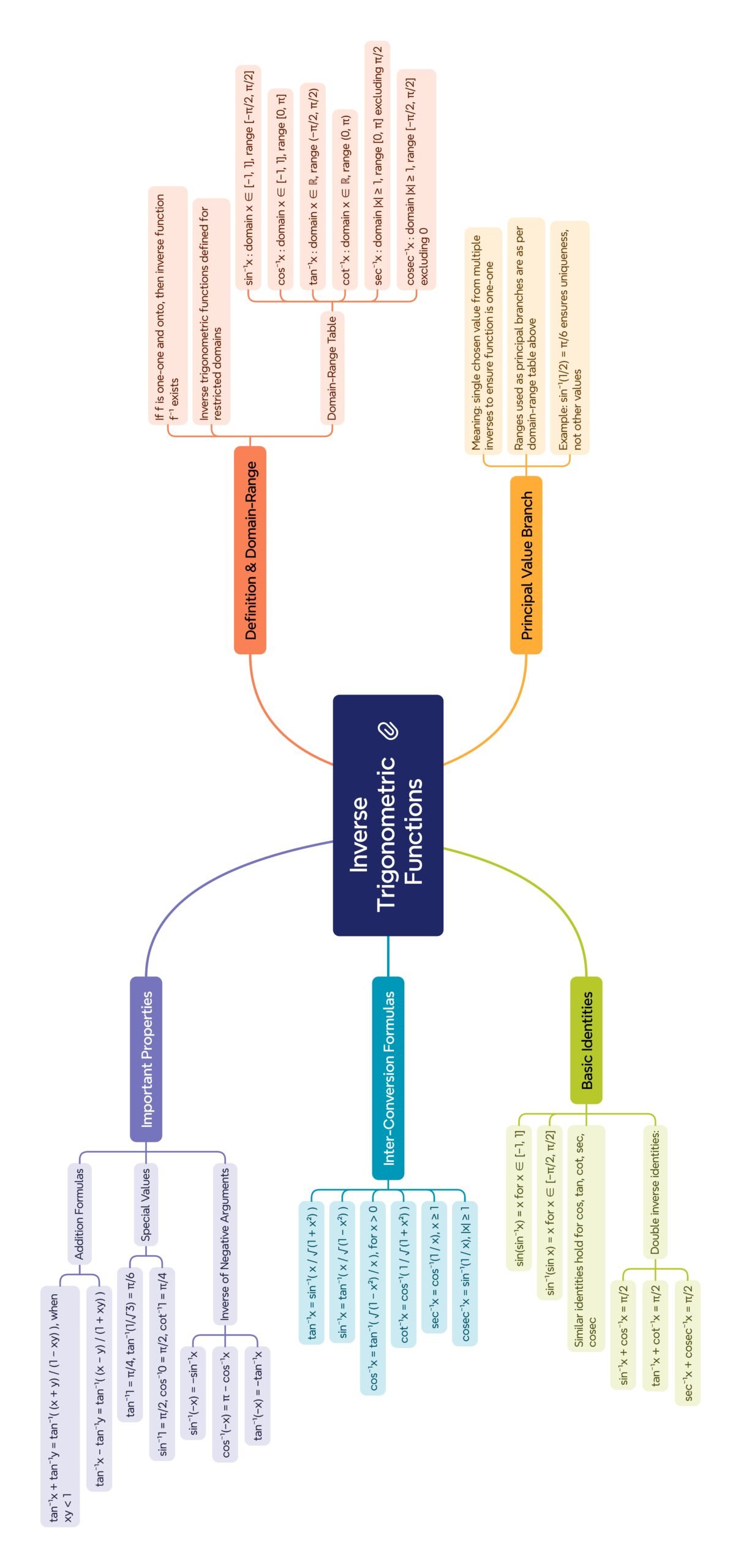
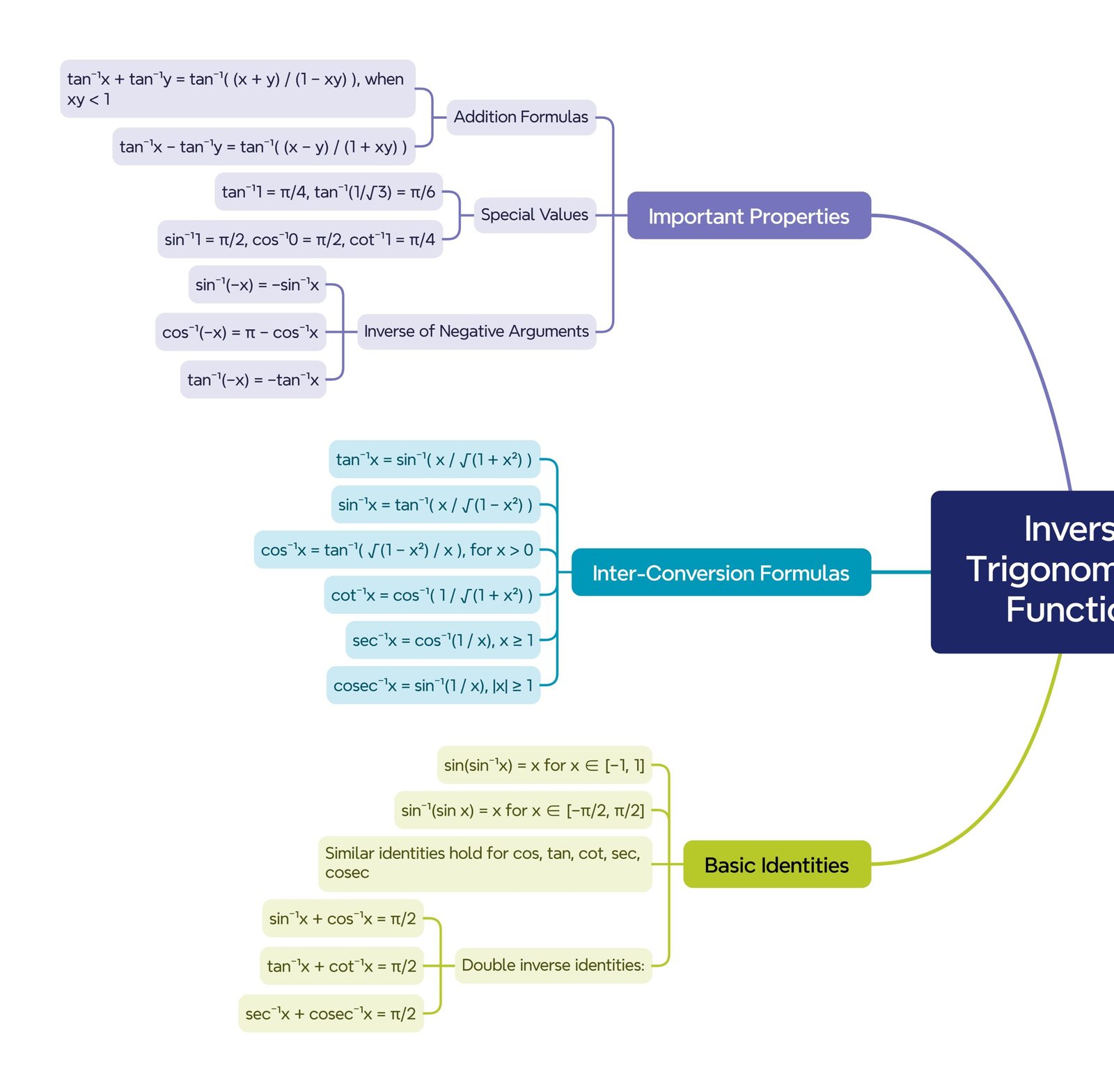
Important Notice : The lessons and study materials up to July–August 2025 have been sent. Soon, after receiving feedback from teachers and students, we will deliver the latest and more innovative study materials for the upcoming months.