Class 11 : Physics (In English) – Chapter 12: Kinetic Theory

Posted by

On June 21, 2025

EXPLANATION & SUMMARY

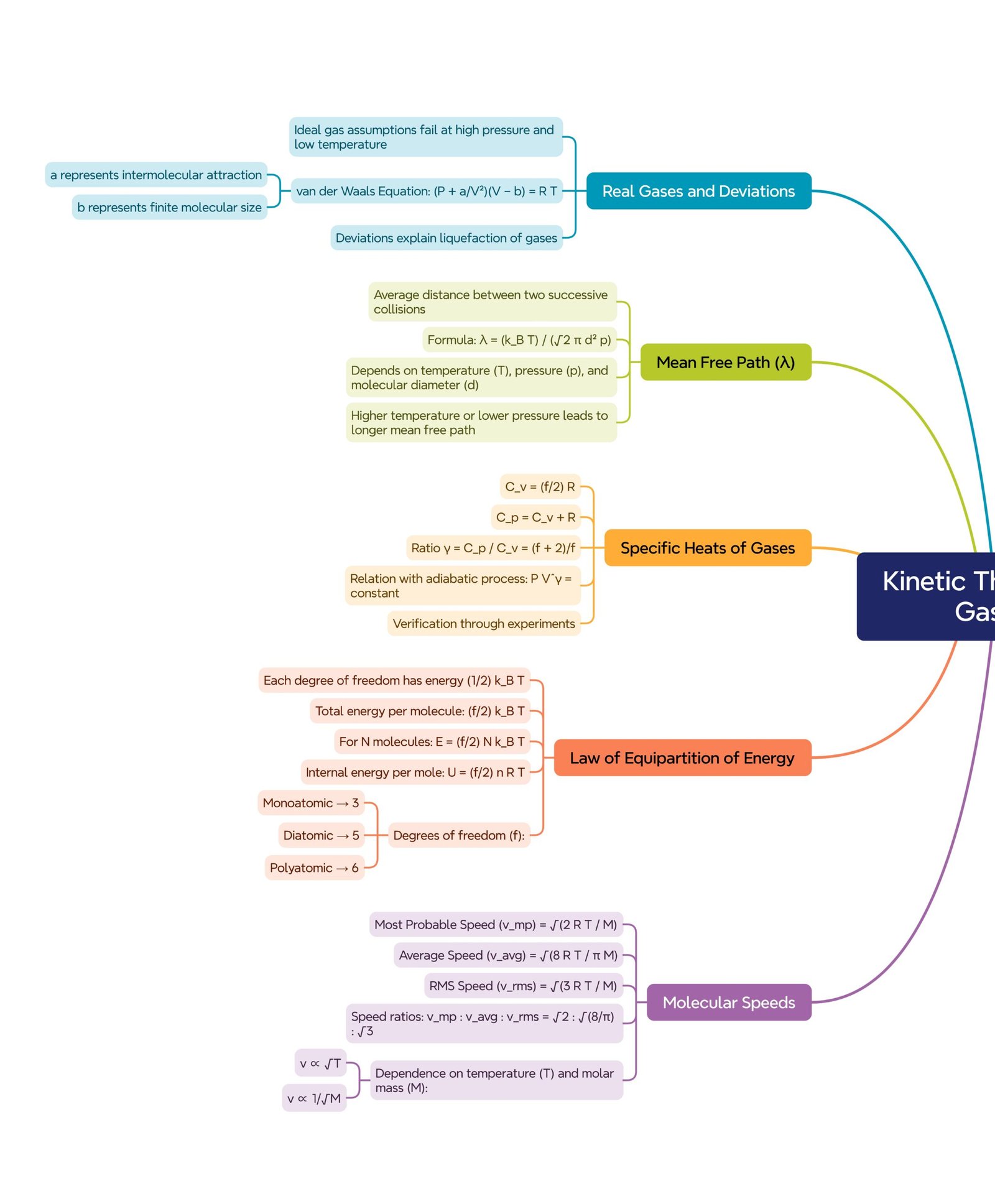
🔵 Introduction to Kinetic Theory
💡 The Kinetic Theory of Gases explains the macroscopic behavior of gases on the basis of molecular motion. It relates the temperature, pressure, and energy of a gas to the motion of its individual molecules.
➡️ It provides a molecular understanding of gas laws like Boyle’s law, Charles’ law, and Avogadro’s law.

🟢 Assumptions of the Kinetic Theory
🔸 A gas consists of a large number of identical molecules in random motion.
🔸 The volume of molecules is negligible compared to the total volume of the gas.
🔸 There are no forces of attraction or repulsion between molecules except during collisions.
🔸 Collisions between molecules and with the container walls are perfectly elastic.
🔸 The time of collision is negligible compared to the time between successive collisions.
🔸 The pressure of a gas arises due to elastic collisions of molecules with the walls.
✏️ Note: These postulates apply to ideal gases only.

🔴 Pressure Due to Molecular Motion
Consider a cubic container of side l having N molecules, each of mass m.
For a single molecule moving with velocity component vₓ, the momentum change on striking a wall and rebounding is:
➡️ Δp = 2m vₓ
Time between successive collisions with the same wall = 2l / vₓ
So, rate of change of momentum = (2m vₓ) / (2l / vₓ) = m vₓ² / l
Hence, pressure due to one molecule:
p₁ = (m vₓ²) / V, where V = l³
For N molecules:
➡️ p = (1/3) n m ⟨v²⟩
where
n = number of molecules per unit volume,
⟨v²⟩ = mean of squared velocities.
Therefore,
➡️ p = (1/3) ρ ⟨v²⟩, where ρ = n·m (density of gas).

🟡 Root Mean Square (RMS) Speed
💡 The RMS speed (vᵣₘₛ) is defined as the square root of the mean of squares of molecular speeds.
➡️ vᵣₘₛ = √(3p / ρ) = √(3RT / M)
where
R = universal gas constant = 8.314 J mol⁻¹ K⁻¹,
M = molar mass of the gas (in kg mol⁻¹),
T = absolute temperature (in K).
✔️ vᵣₘₛ ∝ √T and vᵣₘₛ ∝ 1/√M

🧠 Relation Between Pressure and Kinetic Energy
From the kinetic theory:
p = (1/3) n m ⟨v²⟩
Average kinetic energy per molecule = (1/2) m ⟨v²⟩
Hence,
➡️ p = (2/3) n × (average kinetic energy)
For one mole, total energy:
➡️ E = (3/2) RT
Therefore, for one molecule:
➡️ ε = (3/2) k T, where k = R / N_A (Boltzmann constant).

🔵 Boltzmann Constant
Boltzmann constant links molecular energy to temperature:
➡️ k = R / N_A = 1.38 × 10⁻²³ J·K⁻¹
It provides a bridge between the macroscopic and microscopic descriptions of matter.

🟢 Law of Equipartition of Energy
💡 The law of equipartition of energy states that:
Energy is equally distributed among all degrees of freedom.
If a molecule has f degrees of freedom,
➡️ E_per molecule = (f/2) k T
➡️ E_per mole = (f/2) R T

Examples:
🔹 Monoatomic gas (He, Ne): f = 3 → E = (3/2) k T
🔹 Diatomic gas (O₂, N₂): f = 5 → E = (5/2) k T
🔹 Triatomic gas (CO₂, H₂O): f = 6 → E = (6/2) k T

🔴 Specific Heat Capacities of Gases
At constant volume:
➡️ C_v = (f/2) R
At constant pressure:
➡️ C_p = C_v + R
Ratio of specific heats:
➡️ γ = C_p / C_v = (f + 2)/f
✔️ For monoatomic gas: γ = 5/3
✔️ For diatomic gas: γ = 7/5

🟡 Mean Free Path (λ)
💡 The mean free path is the average distance a molecule travels between two successive collisions.
➡️ λ = k T / (√2 π d² p)
where
d = molecular diameter, p = pressure of gas.
✔️ λ increases with T and decreases with p.

🔵 Real and Ideal Gases
Real gases deviate from ideal behavior because of molecular forces and finite size.
van der Waals’ equation explains this deviation:
➡️ (p + a/V²)(V − b) = R T
where ‘a’ accounts for molecular attraction, and ‘b’ for finite volume.

🟢 Distribution of Molecular Speeds
Not all gas molecules move with the same speed — they follow the Maxwell–Boltzmann distribution.
Three characteristic speeds are defined:
Most probable speed: vₚ = √(2 R T / M)
Average speed: v_avg = √(8 R T / π M)
Root mean square speed: v_rms = √(3 R T / M)
✔️ Their ratio is:
➡️ vₚ : v_avg : v_rms = 1 : 1.13 : 1.22

🔴 Pressure–Temperature Relationship
From p = (1/3) ρ ⟨v²⟩ and ⟨v²⟩ ∝ T,
➡️ p ∝ ρ T
which gives the ideal gas law: p V = n R T

🟡 Brownian Motion
💡 Small particles suspended in a fluid (e.g., pollen grains in water) perform continuous random motion — called Brownian motion.
✔️ It provides direct evidence of molecular motion.

🧠 Avogadro’s Law
Equal volumes of gases under identical conditions of temperature and pressure contain equal numbers of molecules.
➡️ N_A = 6.022 × 10²³ mol⁻¹

🟢 Applications of Kinetic Theory
✔️ Explains pressure, viscosity, and diffusion in gases.
✔️ Provides the basis for temperature, heat, and energy in thermodynamics.
✔️ Supports the concept of molecular nature of matter.

🌟 Summary (≈300 words)
Kinetic theory explains gases as large collections of moving particles whose collisions produce pressure.
Gas pressure: p = (1/3) ρ ⟨v²⟩.
Average kinetic energy of one molecule: (3/2) k T.
Equipartition law: E = (f/2) k T → equal energy per degree of freedom.
Specific heats: C_v = (f/2) R, C_p − C_v = R, γ = (f + 2)/f.
Speeds: vₚ = √(2RT/M), v_avg = √(8RT/πM), v_rms = √(3RT/M); vₚ : v_avg : v_rms = 1 : 1.13 : 1.22.
Mean free path: λ = k T / (√2 π d² p).
Ideal gas law: p V = n R T.
Real gases: (p + a/V²)(V − b) = R T.
Brownian motion supports atomic theory.

📝 Quick Recap
🔹 p = (1/3) ρ ⟨v²⟩
🔹 ε = (3/2) k T
🔹 λ = k T / (√2 π d² p)
🔹 C_p − C_v = R, γ = (f + 2)/f
🔹 vₚ : v_avg : v_rms = 1 : 1.13 : 1.22

————————————————————————————————————————————————————————————————————————————

QUESTIONS FROM TEXTBOOK

🔵 Question 12.1
Estimate the fraction of molecular volume to the actual volume occupied by oxygen gas at STP. Take the diameter of an oxygen molecule to be 3 Å.
Answer
🟢 Step 1: Given data
Diameter = 3 Å = 3×10⁻¹⁰ m ⇒ radius r = 1.5×10⁻¹⁰ m
🟡 Step 2: Volume of one molecule
Vₘₒₗₑcᵤₗₑ = (4/3)πr³ = (4/3)π(1.5×10⁻¹⁰)³ = 1.41×10⁻²⁹ m³
🟠 Step 3: Volume occupied by 1 mol of gas at STP = 22.4 L = 22.4×10⁻³ m³
Number of molecules = 6.02×10²³
Total molecular volume = 6.02×10²³ × 1.41×10⁻²⁹ = 8.49×10⁻⁶ m³
🔴 Step 4: Fraction = 8.49×10⁻⁶ / 22.4×10⁻³ = 3.8×10⁻⁴
✔️ Final Answer: Fraction ≈ 3.8×10⁻⁴ (≈ 0.038 %).

🔵 Question 12.2
Molar volume is the volume occupied by 1 mol of any (ideal) gas at STP (1 atm, 0 °C). Show that it is 22.4 L.
Answer
🟢 Step 1: PV = nRT ⇒ V = RT/P (for n = 1)
🟡 Step 2: R = 8.31 J mol⁻¹ K⁻¹, T = 273 K, P = 1.013×10⁵ Pa
🟠 Step 3: V = (8.31×273)/(1.013×10⁵) = 2.24×10⁻² m³ = 22.4 L
✔️ Final Answer: Molar volume of ideal gas at STP = 22.4 L.

🔵 Question 12.3
Figure 12.8 shows plot of PV/T versus P for 1.00×10⁻³ kg of oxygen gas at two different temperatures.
(a) What does the dotted plot signify?
(b) Which is true: T₁ > T₂ or T₁ < T₂?
(c) What is the value of PV/T where the curves meet on the y-axis?
(d) If similar plots are obtained for 1.00×10⁻⁴ kg of hydrogen, would we get the same PV/T at the intersection? If not, what mass of H₂ yields the same value? (Molecular mass H₂ = 2.02 u, O₂ = 32.0 u, R = 8.31 J mol⁻¹ K⁻¹.)
Answer
(a) The dotted line represents ideal-gas behaviour where PV/T is constant.
(b) At higher T a real gas behaves more ideally (curve closer to dotted line). Hence T₁ < T₂.
(c) At zero pressure, gas is ideal: PV/T = nR.
For 1.00×10⁻³ kg O₂ with M = 32×10⁻³ kg mol⁻¹:
n = m/M = 1.00×10⁻³ / 32×10⁻³ = 0.03125 mol
PV/T = nR = 0.03125×8.31 = 0.2597 J K⁻¹ ≈ 0.26 J K⁻¹.
(d) For hydrogen, PV/T = (m/M)R.
Set equal to 0.2597: 0.2597 = (m / 2.02×10⁻³)×8.31 ⇒ m = 6.32×10⁻⁵ kg.
✔️ Final Answer: Mass of H₂ required = 6.3×10⁻⁵ kg.

🔵 Question 12.4
An oxygen cylinder of volume 30 L has initial pressure 15 atm at 27 °C. After oxygen is withdrawn, pressure drops to 11 atm and temperature to 17 °C. Estimate mass of oxygen taken out. (R = 8.31 J mol⁻¹ K⁻¹; M(O₂) = 32 u.)
Answer
🟢 Step 1: Convert units
V = 30 L = 0.03 m³
P₁ = 15×1.013×10⁵ = 1.52×10⁶ Pa
P₂ = 11×1.013×10⁵ = 1.11×10⁶ Pa
T₁ = 27 + 273 = 300 K; T₂ = 17 + 273 = 290 K
🟡 Step 2: PV/T ∝ n ⇒ Δn = (V/R)[(P₁/T₁) − (P₂/T₂)]
🟠 Step 3: Δn = (0.03/8.31)[(1.52×10⁶/300) − (1.11×10⁶/290)]
= (0.03/8.31)(5067 − 3827) = (0.03×1240)/8.31 = 4.47 mol
🔴 Step 4: Mass = Δn × M = 4.47×32×10⁻³ = 0.143 kg.
✔️ Final Answer: Mass of O₂ taken out = 0.143 kg (≈ 143 g).

🔵 Question 12.5
An air bubble of volume 1.0 cm³ rises from the bottom of a lake 40 m deep at a temperature of 12 °C. To what volume does it grow when it reaches the surface, which is at a temperature of 35 °C?
Answer
🟢 Step 1: Given data
➡️ Depth = 40 m
➡️ V₁ = 1.0 cm³
➡️ T₁ = 12 °C = 285 K
➡️ T₂ = 35 °C = 308 K
Pressure at bottom:
➡️ P₁ = P₀ + hρg = (1.013×10⁵) + (40×1000×9.8) = 4.93×10⁵ Pa
Pressure at surface:
➡️ P₂ = P₀ = 1.013×10⁵ Pa
🟡 Step 2: Using gas law (P₁V₁/T₁ = P₂V₂/T₂)
➡️ V₂ = V₁ × (P₁/P₂) × (T₂/T₁)
➡️ V₂ = 1.0 × (4.93×10⁵ / 1.013×10⁵) × (308 / 285)
➡️ V₂ = 1.0 × 4.87 × 1.08 = 5.26 cm³
✔️ Final Answer: Volume at surface ≈ 5.3 cm³

🔵 Question 12.6
Estimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapour and other constituents) in a room of capacity 25.0 m³ at a temperature of 27 °C and 1 atm pressure.
Answer
🟢 Step 1: Given data
➡️ V = 25.0 m³
➡️ T = 27 + 273 = 300 K
➡️ P = 1.013×10⁵ Pa
➡️ R = 8.31 J mol⁻¹ K⁻¹
🟡 Step 2: Ideal gas law PV = nRT ⇒ n = PV / RT
➡️ n = (1.013×10⁵ × 25.0) / (8.31 × 300)
➡️ n = 3.04×10³ mol
🟠 Step 3: Number of molecules = n × N_A
➡️ N = 3.04×10³ × 6.02×10²³ = 1.83×10²⁷ molecules
✔️ Final Answer: Total air molecules ≈ 1.8×10²⁷

🔵 Question 12.7
Estimate the average thermal energy of a helium atom at
(i) room temperature (27 °C),
(ii) temperature on the surface of the Sun (6000 K),
(iii) temperature of 10 million K.
Answer
🟢 Formula: E = (3/2)kT , where k = 1.38×10⁻²³ J K⁻¹
(i) For T = 300 K
➡️ E₁ = (3/2)(1.38×10⁻²³)(300) = 6.21×10⁻²¹ J
(ii) For T = 6000 K
➡️ E₂ = (3/2)(1.38×10⁻²³)(6000) = 1.24×10⁻¹⁹ J
(iii) For T = 1×10⁷ K
➡️ E₃ = (3/2)(1.38×10⁻²³)(1×10⁷) = 2.07×10⁻¹⁶ J
✔️ Final Answers:
(i) 6.2×10⁻²¹ J
(ii) 1.2×10⁻¹⁹ J
(iii) 2.1×10⁻¹⁶ J

🔵 Question 12.8
Three vessels of equal capacity have gases at the same temperature and pressure. The first vessel contains neon (monatomic), the second chlorine (diatomic), and the third uranium hexafluoride (polyatomic).
Do they contain equal numbers of molecules? Is the rms speed of the molecules the same in all?
Answer
🟢 Step 1: From PV = N k T
➡️ For equal P, V, T ⇒ N (number of molecules) is same.
✔️ So, all three have equal number of molecules.
🟡 Step 2: RMS speed formula
➡️ vᵣₘₛ = √(3kT / m)
Since molecular mass differs (Ne < Cl₂ < UF₆),
➡️ vᵣₘₛ ∝ 1/√m
✔️ Final Answer:
Equal number of molecules, but vᵣₘₛ(Ne) > vᵣₘₛ(Cl₂) > vᵣₘₛ(UF₆)

🔵 Question 12.9
At what temperature is the rms speed of an atom in argon gas equal to that of helium gas at −20 °C?
(Atomic mass: Ar = 39.9 u, He = 4.0 u)
Answer
🟢 Formula: vᵣₘₛ = √(3RT / M)
➡️ For equal speeds: T₁/M₁ = T₂/M₂
➡️ T₁ = T₂ × (M₁ / M₂)
🟡 Given: T(He) = −20 °C = 253 K
➡️ T(Ar) = 253 × (39.9 / 4.0) = 2525 K
✔️ Final Answer: Temperature of Ar = 2525 K (≈ 2250 °C)

🔵 Question 12.10
Estimate the mean free path and collision frequency of a nitrogen molecule in a cylinder containing nitrogen at 2.0 atm and temperature 17 °C.
Take the radius of N₂ molecule ≈ 1.0 Å. Compare the collision time with time between two successive collisions.
(Molecular mass of N₂ = 28 u)
Answer
🟢 Step 1: Given
➡️ P = 2.0 atm = 2.026×10⁵ Pa
➡️ T = 17 + 273 = 290 K
➡️ r = 1.0×10⁻¹⁰ m
➡️ R = 8.31 J mol⁻¹ K⁻¹
🟡 Step 2: Number density n = P / (kT)
➡️ n = (2.026×10⁵) / (1.38×10⁻²³ × 290) = 5.06×10²⁵ m⁻³
🟠 Step 3: Mean free path λ = 1 / (√2 π d² n) , d = 2r = 2×10⁻¹⁰ m
➡️ λ = 1 / (1.414 × 3.14 × (4×10⁻²⁰) × 5.06×10²⁵)
➡️ λ = 1 / (8.99×10⁶) = 1.1×10⁻⁷ m
🔴 Step 4: RMS speed
➡️ vᵣₘₛ = √(3kT/m) = √[(3×1.38×10⁻²³×290)/(4.65×10⁻²⁶)] = 517 m/s
🟣 Step 5: Collision frequency
➡️ Z = vᵣₘₛ / λ = 517 / (1.1×10⁻⁷) = 4.7×10⁹ s⁻¹
✔️ Final Results:
Mean free path = 1.1×10⁻⁷ m
Collision frequency = 4.7×10⁹ s⁻¹
Time between collisions = 1/Z = 2.1×10⁻¹⁰ s

NEET QUESTIONS FROM THIS LESSON

🔴 Question 1 (NEET 2024):
For an ideal gas, average kinetic energy of molecules is proportional to
🟢 1️⃣ Temperature (T)
🟡 2️⃣ Pressure (P)
🔵 3️⃣ Volume (V)
🟣 4️⃣ PV
✅ Answer: 1️⃣ Temperature (T)

🔴 Question 2 (NEET 2023):
The root mean square speed of gas molecules is given by
🟢 1️⃣ √(3kT/m)
🟡 2️⃣ √(3RT/M)
🔵 3️⃣ Both (1) and (2)
🟣 4️⃣ √(2RT/M)
✅ Answer: 3️⃣ Both (1) and (2)

🔴 Question 3 (NEET 2022):
Kinetic energy per molecule of a gas is
🟢 1️⃣ (3/2) kT
🟡 2️⃣ (1/2) kT
🔵 3️⃣ 3kT
🟣 4️⃣ (1/3) kT
✅ Answer: 1️⃣ (3/2) kT

🔴 Question 4 (NEET 2021):
For an ideal gas, internal energy depends on
🟢 1️⃣ Temperature only
🟡 2️⃣ Pressure only
🔵 3️⃣ Volume only
🟣 4️⃣ Both pressure and volume
✅ Answer: 1️⃣ Temperature only

🔴 Question 5 (NEET 2020):
Mean free path of a gas molecule is inversely proportional to
🟢 1️⃣ Number density
🟡 2️⃣ Temperature
🔵 3️⃣ Velocity
🟣 4️⃣ Radius
✅ Answer: 1️⃣ Number density

🔴 Question 6 (NEET 2019):
Which of the following quantities does not depend on temperature for an ideal gas?
🟢 1️⃣ RMS speed
🟡 2️⃣ Pressure
🔵 3️⃣ Average K.E.
🟣 4️⃣ Potential energy
✅ Answer: 4️⃣ Potential energy

🔴 Question 7 (NEET 2018):
If temperature of an ideal gas is doubled, average kinetic energy of molecules
🟢 1️⃣ Doubles
🟡 2️⃣ Halves
🔵 3️⃣ Becomes four times
🟣 4️⃣ Remains same
✅ Answer: 1️⃣ Doubles

🔴 Question 8 (NEET 2017):
The ratio of average speed to RMS speed for a gas is
🟢 1️⃣ √(8/9π)
🟡 2️⃣ √(8/3π)
🔵 3️⃣ √(8/π)
🟣 4️⃣ √(3/8π)
✅ Answer: 2️⃣ √(8/3π)

🔴 Question 9 (NEET 2016):
If pressure of gas is doubled and temperature is constant, mean free path
🟢 1️⃣ Halves
🟡 2️⃣ Doubles
🔵 3️⃣ Same
🟣 4️⃣ Becomes zero
✅ Answer: 1️⃣ Halves

🔴 Question 10 (AIPMT 2015):
Degrees of freedom for a diatomic gas are
🟢 1️⃣ 5
🟡 2️⃣ 3
🔵 3️⃣ 2
🟣 4️⃣ 6
✅ Answer: 1️⃣ 5

🔴 Question 11 (AIPMT 2014):
Pressure exerted by gas molecules is due to
🟢 1️⃣ Elastic collisions
🟡 2️⃣ Inelastic collisions
🔵 3️⃣ Random motion
🟣 4️⃣ Attractive forces
✅ Answer: 1️⃣ Elastic collisions

🔴 Question 12 (AIPMT 2013):
For a gas, average velocity is
🟢 1️⃣ √(8RT/πM)
🟡 2️⃣ √(3RT/M)
🔵 3️⃣ √(2RT/M)
🟣 4️⃣ √(RT/M)
✅ Answer: 1️⃣ √(8RT/πM)

🔴 Question 13 (AIPMT 2012):
If rms velocity is v, average velocity is
🟢 1️⃣ 0.921v
🟡 2️⃣ 0.707v
🔵 3️⃣ 1.225v
🟣 4️⃣ v
✅ Answer: 1️⃣ 0.921v

🔴 Question 14 (AIPMT 2011):
Root mean square speed of gas molecules at temperature T is proportional to
🟢 1️⃣ √T
🟡 2️⃣ T
🔵 3️⃣ 1/T
🟣 4️⃣ 1/√T
✅ Answer: 1️⃣ √T

🔴 Question 15 (AIPMT 2010):
Energy of 1 mole of ideal gas at temperature T is
🟢 1️⃣ (3/2)RT
🟡 2️⃣ (1/2)RT
🔵 3️⃣ (5/2)RT
🟣 4️⃣ RT
✅ Answer: 1️⃣ (3/2)RT

🔴 Question 16 (AIPMT 2009):
For a monoatomic ideal gas, molar specific heat at constant volume is
🟢 1️⃣ (3/2)R
🟡 2️⃣ (5/2)R
🔵 3️⃣ (7/2)R
🟣 4️⃣ (1/2)R
✅ Answer: 1️⃣ (3/2)R

🔴 Question 17 (AIPMT 2008):
Equipartition theorem is applicable to
🟢 1️⃣ Only gases
🟡 2️⃣ All forms of matter
🔵 3️⃣ Only solids
🟣 4️⃣ Only liquids
✅ Answer: 2️⃣ All forms of matter

🔴 Question 18 (AIPMT 2007):
The kinetic theory explains
🟢 1️⃣ Pressure
🟡 2️⃣ Temperature
🔵 3️⃣ Both (1) and (2)
🟣 4️⃣ None
✅ Answer: 3️⃣ Both (1) and (2)

🔴 Question 19 (AIPMT 2006):
The ratio of Cₚ/Cᵥ for monoatomic gas is
🟢 1️⃣ 5/3
🟡 2️⃣ 7/5
🔵 3️⃣ 3/2
🟣 4️⃣ 4/3
✅ Answer: 1️⃣ 5/3

🔴 Question 20 (AIPMT 2005):
Pressure of ideal gas is given by
🟢 1️⃣ (1/3) ρc²
🟡 2️⃣ (2/3) ρc²
🔵 3️⃣ ρc²
🟣 4️⃣ (1/2) ρc²
✅ Answer: 1️⃣ (1/3) ρc²

🔴 Question 21 (AIPMT 2004):
Boltzmann constant k =
🟢 1️⃣ R/Nₐ
🟡 2️⃣ Nₐ/R
🔵 3️⃣ R × Nₐ
🟣 4️⃣ 1/(R × Nₐ)
✅ Answer: 1️⃣ R/Nₐ

🔴 Question 22 (AIPMT 2003):
Mean kinetic energy of gas molecule depends on
🟢 1️⃣ Temperature only
🟡 2️⃣ Pressure only
🔵 3️⃣ Both
🟣 4️⃣ None
✅ Answer: 1️⃣ Temperature only

🔴 Question 23 (AIPMT 2002):
Specific heat of monoatomic gas at constant pressure is
🟢 1️⃣ (5/2)R
🟡 2️⃣ (3/2)R
🔵 3️⃣ R
🟣 4️⃣ 2R
✅ Answer: 1️⃣ (5/2)R

🔴 Question 24 (AIPMT 2001):
The value of γ = Cₚ/Cᵥ for diatomic gas is
🟢 1️⃣ 7/5
🟡 2️⃣ 5/3
🔵 3️⃣ 3/2
🟣 4️⃣ 1
✅ Answer: 1️⃣ 7/5

🔴 Question 25 (NEET 2025):
The average kinetic energy per mole of an ideal gas is
🟢 1️⃣ (3/2)RT
🟡 2️⃣ (1/2)RT
🔵 3️⃣ RT
🟣 4️⃣ 2RT
✅ Answer: 1️⃣ (3/2)RT

🔴 Question 26 (NEET 2024):
If the temperature of a gas is increased from 27°C to 927°C, the RMS speed of the gas molecules becomes
🟢 1️⃣ Twice
🟡 2️⃣ Thrice
🔵 3️⃣ Four times
🟣 4️⃣ Half
✅ Answer: 1️⃣ Twice

🔴 Question 27 (NEET 2023):
The pressure exerted by a gas is due to
🟢 1️⃣ Continuous elastic collisions of molecules with the walls
🟡 2️⃣ Inelastic collisions
🔵 3️⃣ Gravitational pull
🟣 4️⃣ Random motion
✅ Answer: 1️⃣ Continuous elastic collisions of molecules with the walls

🔴 Question 28 (NEET 2022):
The RMS speed of oxygen molecules at 300 K is approximately
🟢 1️⃣ 484 m/s
🟡 2️⃣ 600 m/s
🔵 3️⃣ 300 m/s
🟣 4️⃣ 700 m/s
✅ Answer: 1️⃣ 484 m/s

🔴 Question 29 (NEET 2021):
For an ideal gas, the relation between average, RMS and most probable speeds is
🟢 1️⃣ vₘₚ : v_avg : v_rms = √2 : √3 : 2
🟡 2️⃣ vₘₚ : v_avg : v_rms = 1 : 1.128 : 1.225
🔵 3️⃣ vₘₚ = v_avg = v_rms
🟣 4️⃣ vₘₚ > v_avg > v_rms
✅ Answer: 2️⃣ vₘₚ : v_avg : v_rms = 1 : 1.128 : 1.225

🔴 Question 30 (NEET 2020):
If temperature is increased, mean free path
🟢 1️⃣ Increases
🟡 2️⃣ Decreases
🔵 3️⃣ Remains constant
🟣 4️⃣ Becomes zero
✅ Answer: 1️⃣ Increases

🔴 Question 31 (NEET 2019):
For a monoatomic gas, the ratio Cₚ : Cᵥ is
🟢 1️⃣ 5 : 3
🟡 2️⃣ 3 : 2
🔵 3️⃣ 7 : 5
🟣 4️⃣ 2 : 1
✅ Answer: 1️⃣ 5 : 3

🔴 Question 32 (NEET 2018):
Total energy of one mole of ideal gas at temperature T is
🟢 1️⃣ (3/2)RT
🟡 2️⃣ RT
🔵 3️⃣ (5/2)RT
🟣 4️⃣ (7/2)RT
✅ Answer: 1️⃣ (3/2)RT

🔴 Question 33 (NEET 2017):
According to kinetic theory, pressure P is related to RMS speed c by
🟢 1️⃣ P = (1/3) ρc²
🟡 2️⃣ P = ρc²
🔵 3️⃣ P = (1/2) ρc²
🟣 4️⃣ P = (2/3) ρc²
✅ Answer: 1️⃣ P = (1/3) ρc²

🔴 Question 34 (NEET 2016):
Boltzmann constant is
🟢 1️⃣ 1.38 × 10⁻²³ J/K
🟡 2️⃣ 8.31 J/mol K
🔵 3️⃣ 6.023 × 10²³ J
🟣 4️⃣ 9.8 m/s²
✅ Answer: 1️⃣ 1.38 × 10⁻²³ J/K

🔴 Question 35 (AIPMT 2015):
Average K.E. of a molecule is
🟢 1️⃣ (3/2)kT
🟡 2️⃣ (1/2)kT
🔵 3️⃣ 3kT
🟣 4️⃣ (1/3)kT
✅ Answer: 1️⃣ (3/2)kT

🔴 Question 36 (AIPMT 2014):
If average kinetic energy is doubled, temperature becomes
🟢 1️⃣ Double
🟡 2️⃣ Half
🔵 3️⃣ Same
🟣 4️⃣ Four times
✅ Answer: 1️⃣ Double

🔴 Question 37 (AIPMT 2013):
Equipartition law holds good for
🟢 1️⃣ All gases
🟡 2️⃣ Only ideal gases
🔵 3️⃣ Solids
🟣 4️⃣ Liquids
✅ Answer: 1️⃣ All gases

🔴 Question 38 (AIPMT 2012):
If temperature increases four times, RMS speed becomes
🟢 1️⃣ Twice
🟡 2️⃣ Four times
🔵 3️⃣ Half
🟣 4️⃣ One-fourth
✅ Answer: 1️⃣ Twice

🔴 Question 39 (AIPMT 2011):
For diatomic gas, total energy is
🟢 1️⃣ (5/2)RT
🟡 2️⃣ (3/2)RT
🔵 3️⃣ RT
🟣 4️⃣ 2RT
✅ Answer: 1️⃣ (5/2)RT

🔴 Question 40 (AIPMT 2010):
The kinetic theory explains
🟢 1️⃣ Boyle’s law
🟡 2️⃣ Charles’s law
🔵 3️⃣ Both (1) and (2)
🟣 4️⃣ None
✅ Answer: 3️⃣ Both (1) and (2)

🔴 Question 41 (AIPMT 2009):
According to kinetic theory, gas molecules exert pressure due to
🟢 1️⃣ Elastic collisions
🟡 2️⃣ Gravity
🔵 3️⃣ Attraction
🟣 4️⃣ Repulsion
✅ Answer: 1️⃣ Elastic collisions

🔴 Question 42 (AIPMT 2008):
The number of degrees of freedom for monoatomic gas is
🟢 1️⃣ 3
🟡 2️⃣ 5
🔵 3️⃣ 2
🟣 4️⃣ 6
✅ Answer: 1️⃣ 3

🔴 Question 43 (AIPMT 2007):
Ratio of RMS speed at 127°C and 27°C is
🟢 1️⃣ √(400/300) = √(4/3)
🟡 2️⃣ √(3/4)
🔵 3️⃣ 2
🟣 4️⃣ 1
✅ Answer: 1️⃣ √(4/3)

🔴 Question 44 (AIPMT 2006):
If gas pressure increases and temperature constant, mean free path
🟢 1️⃣ Decreases
🟡 2️⃣ Increases
🔵 3️⃣ Constant
🟣 4️⃣ Zero
✅ Answer: 1️⃣ Decreases

🔴 Question 45 (AIPMT 2005):
For monoatomic gas, internal energy per mole is
🟢 1️⃣ (3/2)RT
🟡 2️⃣ (5/2)RT
🔵 3️⃣ (1/2)RT
🟣 4️⃣ RT
✅ Answer: 1️⃣ (3/2)RT

🔴 Question 46 (AIPMT 2004):
If temperature doubles, RMS speed increases by
🟢 1️⃣ √2 times
🟡 2️⃣ 2 times
🔵 3️⃣ 4 times
🟣 4️⃣ Remains same
✅ Answer: 1️⃣ √2 times

🔴 Question 47 (AIPMT 2003):
Pressure of gas proportional to
🟢 1️⃣ Mean square speed
🟡 2️⃣ Mean speed
🔵 3️⃣ Average speed
🟣 4️⃣ Square root of speed
✅ Answer: 1️⃣ Mean square speed

🔴 Question 48 (AIPMT 2002):
RMS velocity of hydrogen at 27°C is
🟢 1️⃣ 1930 m/s
🟡 2️⃣ 1000 m/s
🔵 3️⃣ 484 m/s
🟣 4️⃣ 273 m/s
✅ Answer: 1️⃣ 1930 m/s

🔴 Question 49 (AIPMT 2001):
Gas equation derived from kinetic theory is
🟢 1️⃣ PV = (1/3)Nm⟨c²⟩
🟡 2️⃣ PV = nRT
🔵 3️⃣ PV = NkT
🟣 4️⃣ All of these
✅ Answer: 1️⃣ PV = (1/3)Nm⟨c²⟩

🔴 Question 50 (NEET 2025):
Average kinetic energy of gas molecule is
🟢 1️⃣ (3/2)kT
🟡 2️⃣ (1/2)kT
🔵 3️⃣ 3kT
🟣 4️⃣ kT
✅ Answer: 1️⃣ (3/2)kT

JEE MAINS QUESTIONS FROM THIS LESSON

🔴 Q1. According to kinetic theory, pressure of a gas is due to
🟢 1️⃣ Elastic collisions of molecules with walls
🔵 2️⃣ Gravitational pull
🟡 3️⃣ Viscosity
🟣 4️⃣ Volume of molecules
✔️ Answer: 1
📘 Exam: JEE Main 2024

🔴 Q2. Root mean square speed of gas molecules is proportional to
🟢 1️⃣ √T
🔵 2️⃣ T
🟡 3️⃣ 1/T
🟣 4️⃣ 1/√T
✔️ Answer: 1
📘 Exam: JEE Main 2024

🔴 Q3. The average kinetic energy of gas molecules depends on
🟢 1️⃣ Temperature
🔵 2️⃣ Pressure
🟡 3️⃣ Volume
🟣 4️⃣ Density
✔️ Answer: 1
📘 Exam: JEE Main 2023

🔴 Q4. RMS speed of gas molecules is given by
🟢 1️⃣ √(3RT/M)
🔵 2️⃣ √(RT/3M)
🟡 3️⃣ 3RT/M
🟣 4️⃣ RT/M
✔️ Answer: 1
📘 Exam: JEE Main 2023

🔴 Q5. At constant temperature, if pressure increases, mean free path
🟢 1️⃣ Decreases
🔵 2️⃣ Increases
🟡 3️⃣ Constant
🟣 4️⃣ Infinite
✔️ Answer: 1
📘 Exam: JEE Main 2022

🔴 Q6. The ratio of root mean square velocity to average velocity is
🟢 1️⃣ √(3π/8)
🔵 2️⃣ √(8/3π)
🟡 3️⃣ √(π/2)
🟣 4️⃣ √(2/π)
✔️ Answer: 1
📘 Exam: JEE Main 2022

🔴 Q7. For an ideal gas, internal energy U =
🟢 1️⃣ (3/2) nRT
🔵 2️⃣ nRT
🟡 3️⃣ PV
🟣 4️⃣ Constant
✔️ Answer: 1
📘 Exam: JEE Main 2021

🔴 Q8. The kinetic energy of 1 mole of an ideal gas at temperature T is
🟢 1️⃣ (3/2)RT
🔵 2️⃣ RT
🟡 3️⃣ (1/2)RT
🟣 4️⃣ 2RT
✔️ Answer: 1
📘 Exam: JEE Main 2021

🔴 Q9. Mean free path is inversely proportional to
🟢 1️⃣ Number density
🔵 2️⃣ Temperature
🟡 3️⃣ Volume
🟣 4️⃣ RMS speed
✔️ Answer: 1
📘 Exam: JEE Main 2020

🔴 Q10. If temperature of gas is doubled, RMS speed increases by
🟢 1️⃣ √2 times
🔵 2 times
🟡 4 times
🟣 1/2 times
✔️ Answer: 1
📘 Exam: JEE Main 2020

🔴 Q11. Pressure exerted by gas on walls is due to
🟢 1️⃣ Collisions of molecules
🔵 2️⃣ Weight of gas
🟡 3️⃣ Intermolecular attraction
🟣 4️⃣ Volume of gas
✔️ Answer: 1
📘 Exam: JEE Main 2019

🔴 Q12. The relation between RMS, average, and most probable speeds is
🟢 1️⃣ vrms : vavg : vmp = √3 : √(8/π) : √2
🔵 2️⃣ vrms > vavg > vmp
🟡 3️⃣ vrms < vavg < vmp
🟣 4️⃣ vrms = vavg = vmp
✔️ Answer: 2
📘 Exam: JEE Main 2019

🔴 Q13. The equation for pressure from kinetic theory is
🟢 1️⃣ P = (1/3)ρc²
🔵 2️⃣ P = ρc²
🟡 3️⃣ P = (2/3)ρc²
🟣 4️⃣ P = (1/2)ρc²
✔️ Answer: 1
📘 Exam: JEE Main 2018

🔴 Q14. The value of Boltzmann constant is
🟢 1️⃣ 1.38 × 10⁻²³ J/K
🔵 2️⃣ 8.31 J/mol·K
🟡 3️⃣ 6.62 × 10⁻³⁴ J·s
🟣 4️⃣ 9.1 × 10⁻³¹ kg
✔️ Answer: 1
📘 Exam: JEE Main 2018

🔴 Q15. For a gas, pressure is related to RMS speed as
🟢 1️⃣ P ∝ vrms²
🔵 2️⃣ P ∝ vrms
🟡 3️⃣ P ∝ 1/vrms
🟣 4️⃣ P ∝ 1/vrms²
✔️ Answer: 1
📘 Exam: JEE Main 2017

🔴 Q16. The temperature at which RMS speed of O₂ equals that of H₂ at 50 K is
🟢 1️⃣ 800 K
🔵 2️⃣ 400 K
🟡 3️⃣ 100 K
🟣 4️⃣ 50 K
✔️ Answer: 1
📘 Exam: JEE Main 2017

🔴 Q17. The RMS speed of oxygen at 300 K is about
🟢 1️⃣ 484 m/s
🔵 2️⃣ 242 m/s
🟡 3️⃣ 968 m/s
🟣 4️⃣ 100 m/s
✔️ Answer: 1
📘 Exam: JEE Main 2016

🔴 Q18. If gas pressure is doubled at constant temperature, RMS speed
🟢 1️⃣ Remains same
🔵 2️⃣ Doubles
🟡 3️⃣ Halves
🟣 4️⃣ Becomes zero
✔️ Answer: 1
📘 Exam: JEE Main 2016

🔴 Q19. Energy of each degree of freedom is
🟢 1️⃣ (1/2)kT
🔵 2️⃣ kT
🟡 3️⃣ (3/2)kT
🟣 4️⃣ Zero
✔️ Answer: 1
📘 Exam: JEE Main 2015

🔴 Q20. The total energy of a monoatomic gas with n moles at temperature T is
🟢 1️⃣ (3/2)nRT
🔵 2️⃣ nRT
🟡 3️⃣ (1/2)nRT
🟣 4️⃣ 3nRT
✔️ Answer: 1
📘 Exam: JEE Main 2015

🔴 Q21. The RMS velocity of hydrogen molecule at 300 K is approximately
🟢 1️⃣ 1930 m/s
🔵 2️⃣ 1370 m/s
🟡 3️⃣ 700 m/s
🟣 4️⃣ 484 m/s
✔️ Answer: 1
📘 Exam: JEE Main 2014

🔴 Q22. At what temperature will the RMS speed of oxygen be twice its value at 300 K?
🟢 1️⃣ 1200 K
🔵 2️⃣ 600 K
🟡 3️⃣ 900 K
🟣 4️⃣ 150 K
✔️ Answer: 1
📘 Exam: JEE Main 2014

🔴 Q23. Pressure exerted by 1 mole of gas is proportional to
🟢 1️⃣ T/V
🔵 2️⃣ V/T
🟡 3️⃣ 1/V²
🟣 4️⃣ T²/V
✔️ Answer: 1
📘 Exam: JEE Main 2013

🔴 Q24. The RMS speed of a gas molecule is equal to average speed when
🟢 1️⃣ All molecules move at same speed
🔵 2️⃣ T = 0
🟡 3️⃣ P = 0
🟣 4️⃣ V = 0
✔️ Answer: 1
📘 Exam: JEE Main 2013

🔴 Q25. The average translational kinetic energy per molecule is
🟢 1️⃣ (3/2)kT
🔵 2️⃣ (1/2)kT
🟡 3️⃣ (1/3)kT
🟣 4️⃣ kT
✔️ Answer: 1
📘 Exam: JEE Main 2012

🔴 Q26. For a gas at constant temperature, the product of pressure and volume is
🟢 1️⃣ Constant
🔵 2️⃣ Inversely proportional to temperature
🟡 3️⃣ Directly proportional to density
🟣 4️⃣ Zero
✔️ Answer: 1
📘 Exam: JEE Main 2011

🔴 Q27. The ratio of RMS speeds of hydrogen and oxygen at the same temperature is
🟢 1️⃣ 4 : 1
🔵 2️⃣ 1 : 4
🟡 3️⃣ 2 : 1
🟣 4️⃣ 1 : 2
✔️ Answer: 1
📘 Exam: JEE Main 2011

🔴 Q28. Mean kinetic energy of one mole of ideal gas at temperature T is
🟢 1️⃣ (3/2)RT
🔵 2️⃣ RT
🟡 3️⃣ (1/2)RT
🟣 4️⃣ 2RT
✔️ Answer: 1
📘 Exam: JEE Main 2010

🔴 Q29. At a given temperature, the average kinetic energy of helium and oxygen molecules is
🟢 1️⃣ Same
🔵 2️⃣ Double for helium
🟡 3️⃣ Double for oxygen
🟣 4️⃣ None of these
✔️ Answer: 1
📘 Exam: JEE Main 2010

🔴 Q30. The RMS speed of gas molecules is proportional to
🟢 1️⃣ √(Temperature / Molar mass)
🔵 2️⃣ Temperature × Molar mass
🟡 3️⃣ Temperature / Molar mass²
🟣 4️⃣ √(Molar mass / Temperature)
✔️ Answer: 1
📘 Exam: JEE Main 2009

🔴 Q31. For an ideal gas, the average kinetic energy per molecule is
🟢 1️⃣ (3/2)kT
🔵 2️⃣ (1/2)kT
🟡 3️⃣ 3kT
🟣 4️⃣ kT
✔️ Answer: 1
📘 Exam: JEE Main 2009

🔴 Q32. Kinetic energy of gas molecules depends only on
🟢 1️⃣ Temperature
🔵 2️⃣ Volume
🟡 3️⃣ Pressure
🟣 4️⃣ Density
✔️ Answer: 1
📘 Exam: JEE Main 2008

🔴 Q33. The ratio of speeds for gases A and B at same temperature is √(M_B / M_A). This is
🟢 1️⃣ Graham’s law
🔵 2️⃣ Boyle’s law
🟡 3️⃣ Dalton’s law
🟣 4️⃣ Charles’ law
✔️ Answer: 1
📘 Exam: JEE Main 2008

🔴 Q34. RMS speed of nitrogen at 27°C is v. Its RMS speed at 927°C will be
🟢 1️⃣ √2 v
🔵 2️⃣ 2v
🟡 3️⃣ v/2
🟣 4️⃣ v/√2
✔️ Answer: 1
📘 Exam: JEE Main 2007

🔴 Q35. The mean kinetic energy of 1 mole of gas at 300 K is
🟢 1️⃣ (3/2) × 8.31 × 300 J
🔵 2️⃣ (1/2) × 8.31 × 300 J
🟡 3️⃣ 8.31 × 300 J
🟣 4️⃣ 3 × 8.31 × 300 J
✔️ Answer: 1
📘 Exam: JEE Main 2007

🔴 Q36. RMS velocity of gas molecules at 0°C and 1 atm is v. At 0°C and 4 atm, it will be
🟢 1️⃣ v
🔵 2️⃣ 2v
🟡 3️⃣ v/2
🟣 4️⃣ 4v
✔️ Answer: 1
📘 Exam: JEE Main 2006

🔴 Q37. At 27°C, RMS velocity of oxygen molecules is v. The temperature at which it becomes 2v is
🟢 1️⃣ 927°C
🔵 2️⃣ 1227°C
🟡 3️⃣ 327°C
🟣 4️⃣ 127°C
✔️ Answer: 2
📘 Exam: JEE Main 2006

🔴 Q38. Pressure of gas is due to
🟢 1️⃣ Momentum transfer of molecules
🔵 2️⃣ Weight of gas
🟡 3️⃣ Random motion
🟣 4️⃣ Intermolecular attraction
✔️ Answer: 1
📘 Exam: JEE Main 2005

🔴 Q39. RMS velocity of hydrogen at 300 K is about
🟢 1️⃣ 1930 m/s
🔵 2️⃣ 1370 m/s
🟡 3️⃣ 700 m/s
🟣 4️⃣ 484 m/s
✔️ Answer: 1
📘 Exam: JEE Main 2005

🔴 Q40. For a diatomic gas, degrees of freedom =
🟢 1️⃣ 5
🔵 2️⃣ 3
🟡 3️⃣ 6
🟣 4️⃣ 2
✔️ Answer: 1
📘 Exam: JEE Main 2004

🔴 Q41. The ratio of energies of diatomic to monoatomic gas at same T is
🟢 1️⃣ 5 : 3
🔵 2️⃣ 3 : 5
🟡 3️⃣ 1 : 1
🟣 4️⃣ 2 : 1
✔️ Answer: 1
📘 Exam: JEE Main 2004

🔴 Q42. In kinetic theory, gas pressure is due to
🟢 1️⃣ Elastic collision
🔵 2️⃣ Inelastic collision
🟡 3️⃣ Both
🟣 4️⃣ None
✔️ Answer: 1
📘 Exam: JEE Main 2003

🔴 Q43. The equation PV = (1/3)Nm c² shows that
🟢 1️⃣ P ∝ c²
🔵 2️⃣ P ∝ c
🟡 3️⃣ P ∝ 1/c²
🟣 4️⃣ P ∝ 1/c
✔️ Answer: 1
📘 Exam: JEE Main 2003

🔴 Q44. The RMS speed of molecules depends on
🟢 1️⃣ Temperature
🔵 2️⃣ Pressure
🟡 3️⃣ Volume
🟣 4️⃣ Density
✔️ Answer: 1
📘 Exam: JEE Main 2002

🔴 Q45. The ratio of RMS velocities of two gases is √(T₁M₂ / T₂M₁). It is
🟢 1️⃣ Graham’s law
🔵 2️⃣ Boyle’s law
🟡 3️⃣ Dalton’s law
🟣 4️⃣ Avogadro’s law
✔️ Answer: 1
📘 Exam: JEE Main 2002

🔴 Q46. For monoatomic gas, Cp/Cv =
🟢 1️⃣ 5/3
🔵 2️⃣ 7/5
🟡 3️⃣ 3/2
🟣 4️⃣ 2
✔️ Answer: 1
📘 Exam: JEE Main 2001

🔴 Q47. At 0°C, RMS velocity of nitrogen molecule is
🟢 1️⃣ 493 m/s
🔵 2️⃣ 300 m/s
🟡 3️⃣ 600 m/s
🟣 4️⃣ 200 m/s
✔️ Answer: 1
📘 Exam: JEE Main 2001

🔴 Q48. The RMS velocity of oxygen at 300 K is about
🟢 1️⃣ 484 m/s
🔵 2️⃣ 242 m/s
🟡 3️⃣ 968 m/s
🟣 4️⃣ 100 m/s
✔️ Answer: 1
📘 Exam: JEE Main 2001

🔴 Q49. According to equipartition theorem, energy per molecule =
🟢 1️⃣ (f/2)kT
🔵 2️⃣ fkT
🟡 3️⃣ (1/f)kT
🟣 4️⃣ 0
✔️ Answer: 1
📘 Exam: JEE Main 2001

🔴 Q50. The mean translational kinetic energy of gas molecule is
🟢 1️⃣ (3/2)kT
🔵 2️⃣ (1/2)kT
🟡 3️⃣ kT
🟣 4️⃣ (2/3)kT
✔️ Answer: 1
📘 Exam: JEE Main 2001

JEE ADVANCED QUESTIONS FROM THIS LESSON

🔴 Question 1:
According to kinetic theory, the pressure of an ideal gas is due to
🟢 1️⃣ Elastic collisions of molecules with container walls
🔵 2️⃣ Inelastic collisions of molecules
🟡 3️⃣ Intermolecular forces
🟣 4️⃣ Gravity
✔️ Answer: Elastic collisions of molecules with container walls
📘 Exam: JEE Advanced 2024 (Paper 1)

🔴 Question 2:
For an ideal gas, the average kinetic energy per molecule is
🟢 1️⃣ (3/2) kT
🔵 2️⃣ (1/2) kT
🟡 3️⃣ kT
🟣 4️⃣ (5/2) kT
✔️ Answer: (3/2) kT
📘 Exam: JEE Advanced 2023 (Paper 1)

🔴 Question 3:
The root mean square speed of gas molecules is proportional to
🟢 1️⃣ √T
🔵 2️⃣ T
🟡 3️⃣ 1/T
🟣 4️⃣ 1/√T
✔️ Answer: √T
📘 Exam: JEE Advanced 2022 (Paper 1)

🔴 Question 4:
For two gases at the same temperature, ratio of their rms speeds is proportional to
🟢 1️⃣ √(M₂/M₁)
🔵 2️⃣ √(M₁/M₂)
🟡 3️⃣ M₁/M₂
🟣 4️⃣ M₂/M₁
✔️ Answer: √(M₂/M₁)
📘 Exam: JEE Advanced 2021 (Paper 1)

🔴 Question 5:
Mean free path is
🟢 1️⃣ Inversely proportional to number density
🔵 2️⃣ Directly proportional to number density
🟡 3️⃣ Inversely proportional to temperature
🟣 4️⃣ Constant
✔️ Answer: Inversely proportional to number density
📘 Exam: JEE Advanced 2020 (Paper 1)

🔴 Question 6:
For an ideal gas, internal energy depends on
🟢 1️⃣ Temperature
🔵 2️⃣ Pressure
🟡 3️⃣ Volume
🟣 4️⃣ Number of molecules
✔️ Answer: Temperature
📘 Exam: JEE Advanced 2019 (Paper 1)

🔴 Question 7:
The ratio of rms velocity to average velocity for a gas is
🟢 1️⃣ √(3π/8)
🔵 2️⃣ √(8/3π)
🟡 3️⃣ √(3/2)
🟣 4️⃣ 1
✔️ Answer: √(3π/8)
📘 Exam: JEE Advanced 2018 (Paper 1)

🔴 Question 8:
The average kinetic energy of one mole of gas molecules is
🟢 1️⃣ (3/2) RT
🔵 2️⃣ (1/2) RT
🟡 3️⃣ RT
🟣 4️⃣ (5/2) RT
✔️ Answer: (3/2) RT
📘 Exam: JEE Advanced 2017 (Paper 1)

🔴 Question 9:
For two gases A and B, if rms speed of A is twice that of B, then ratio of their molecular masses M_A : M_B is
🟢 1️⃣ 1 : 4
🔵 2️⃣ 4 : 1
🟡 3️⃣ 2 : 1
🟣 4️⃣ 1 : 2
✔️ Answer: 1 : 4
📘 Exam: JEE Advanced 2016 (Paper 1)

🔴 Question 10:
The rms speed of O₂ molecules at 300 K is approximately
🟢 1️⃣ 484 m/s
🔵 2️⃣ 400 m/s
🟡 3️⃣ 600 m/s
🟣 4️⃣ 200 m/s
✔️ Answer: 484 m/s
📘 Exam: JEE Advanced 2015 (Paper 1)

🔴 Question 11:
If pressure and temperature of gas are doubled, rms speed becomes
🟢 1️⃣ √2 times
🔵 2️⃣ 2 times
🟡 3️⃣ 4 times
🟣 4️⃣ Same
✔️ Answer: √2 times
📘 Exam: JEE Advanced 2014 (Paper 1)

🔴 Question 12:
The kinetic theory of gases assumes that
🟢 1️⃣ Intermolecular forces are negligible
🔵 2️⃣ Molecules attract each other
🟡 3️⃣ Molecules repel each other
🟣 4️⃣ Collisions are inelastic
✔️ Answer: Intermolecular forces are negligible
📘 Exam: JEE Advanced 2013 (Paper 1)

🔴 Question 13:
For a gas, average speed is
🟢 1️⃣ √(8RT/πM)
🔵 2️⃣ √(3RT/M)
🟡 3️⃣ √(2RT/M)
🟣 4️⃣ RT/M
✔️ Answer: √(8RT/πM)
📘 Exam: JEE Advanced 2012 (Paper 1)

🔴 Question 14:
The pressure of gas is doubled, temperature constant, mean free path becomes
🟢 1️⃣ Halved
🔵 2️⃣ Doubled
🟡 3️⃣ Same
🟣 4️⃣ Zero
✔️ Answer: Halved
📘 Exam: JEE Advanced 2011 (Paper 1)

🔴 Question 15:
If the temperature of gas increases, mean free path
🟢 1️⃣ Increases
🔵 2️⃣ Decreases
🟡 3️⃣ Remains same
🟣 4️⃣ Becomes zero
✔️ Answer: Increases
📘 Exam: JEE Advanced 2010 (Paper 1)

🔴 Question 16:
The ratio of most probable speed to rms speed is
🟢 1️⃣ √(2/3)
🔵 2️⃣ √(3/2)
🟡 3️⃣ 1
🟣 4️⃣ √(π/2)
✔️ Answer: √(2/3)
📘 Exam: JEE Advanced 2009 (Paper 1)

🔴 Question 17:
For an ideal gas, which of the following is constant in all processes?
🟢 1️⃣ Ratio U/T
🔵 2️⃣ U/P
🟡 3️⃣ U/V
🟣 4️⃣ P/T
✔️ Answer: Ratio U/T
📘 Exam: JEE Advanced 2008 (Paper 1)

🔴 Question 18:
If the rms speed of gas molecules is doubled, the temperature becomes
🟢 1️⃣ 2T
🔵 2️⃣ 4T
🟡 3️⃣ T/2
🟣 4️⃣ T/4
✔️ Answer: 4T
📘 Exam: JEE Advanced 2024 (Paper 2)

🔴 Question 19:
At constant temperature, if pressure of a gas is doubled, the rms speed
🟢 1️⃣ Doubles
🔵 2️⃣ Halves
🟡 3️⃣ Remains same
🟣 4️⃣ Becomes zero
✔️ Answer: Remains same
📘 Exam: JEE Advanced 2023 (Paper 2)

🔴 Question 20:
For one mole of gas, the average kinetic energy is
🟢 1️⃣ (3/2)RT
🔵 2️⃣ (1/2)RT
🟡 3️⃣ RT
🟣 4️⃣ (5/2)RT
✔️ Answer: (3/2)RT
📘 Exam: JEE Advanced 2022 (Paper 2)

🔴 Question 21:
Ratio of rms speeds of H₂ and O₂ at same temperature is
🟢 1️⃣ 1 : 4
🔵 2️⃣ 4 : 1
🟡 3️⃣ 1 : 2
🟣 4️⃣ 2 : 1
✔️ Answer: 4 : 1
📘 Exam: JEE Advanced 2021 (Paper 2)

🔴 Question 22:
The mean free path λ is inversely proportional to
🟢 1️⃣ Pressure
🔵 2️⃣ Temperature
🟡 3️⃣ Radius of molecule
🟣 4️⃣ Square of radius
✔️ Answer: Pressure
📘 Exam: JEE Advanced 2020 (Paper 2)

🔴 Question 23:
In kinetic theory, pressure P is given by
🟢 1️⃣ P = (1/3) nmv²
🔵 2️⃣ P = nmv²
🟡 3️⃣ P = (2/3) nmv²
🟣 4️⃣ P = (1/2) nmv²
✔️ Answer: P = (1/3) nmv²
📘 Exam: JEE Advanced 2019 (Paper 2)

🔴 Question 24:
In an ideal gas, if temperature increases by 100%, rms speed
🟢 1️⃣ Increases by 100%
🔵 2️⃣ Increases by 41%
🟡 3️⃣ Increases by 50%
🟣 4️⃣ Doubles
✔️ Answer: Increases by 41%
📘 Exam: JEE Advanced 2018 (Paper 2)

🔴 Question 25:
Which of the following is true for ideal gas?
🟢 1️⃣ U ∝ T
🔵 2️⃣ U ∝ P
🟡 3️⃣ U ∝ V
🟣 4️⃣ U ∝ n²
✔️ Answer: U ∝ T
📘 Exam: JEE Advanced 2017 (Paper 2)

🔴 Question 26:
If rms velocity of O₂ molecules is 480 m/s at T = 300 K, the rms velocity at 1200 K is
🟢 1️⃣ 960 m/s
🔵 2️⃣ 240 m/s
🟡 3️⃣ 600 m/s
🟣 4️⃣ 1920 m/s
✔️ Answer: 960 m/s
📘 Exam: JEE Advanced 2016 (Paper 2)

🔴 Question 27:
The ratio of most probable speed to average speed is
🟢 1️⃣ √(π/4)
🔵 2️⃣ √(4/π)
🟡 3️⃣ √(2/3)
🟣 4️⃣ √(3/2)
✔️ Answer: √(π/4)
📘 Exam: JEE Advanced 2015 (Paper 2)

🔴 Question 28:
If number density is doubled and temperature remains constant, mean free path
🟢 1️⃣ Doubles
🔵 2️⃣ Halves
🟡 3️⃣ Same
🟣 4️⃣ Zero
✔️ Answer: Halves
📘 Exam: JEE Advanced 2014 (Paper 2)

🔴 Question 29:
If pressure of gas increases four times, mean free path becomes
🟢 1️⃣ 1/4
🔵 2️⃣ 4
🟡 3️⃣ 2
🟣 4️⃣ 1/2
✔️ Answer: 1/4
📘 Exam: JEE Advanced 2013 (Paper 2)

🔴 Question 30:
The kinetic energy of 1 mole of gas at 27°C is
🟢 1️⃣ 3RT/2
🔵 2️⃣ RT/2
🟡 3️⃣ RT
🟣 4️⃣ 5RT/2
✔️ Answer: 3RT/2
📘 Exam: JEE Advanced 2012 (Paper 2)

🔴 Question 31:
If gas temperature is doubled, most probable speed changes by
🟢 1️⃣ √2 times
🔵 2️⃣ 2 times
🟡 3️⃣ 1/√2 times
🟣 4️⃣ Remains same
✔️ Answer: √2 times
📘 Exam: JEE Advanced 2011 (Paper 2)

🔴 Question 32:
The rms velocity of gas molecules at 0°C is 500 m/s. At 100°C it will be approximately
🟢 1️⃣ 540 m/s
🔵 2️⃣ 1000 m/s
🟡 3️⃣ 250 m/s
🟣 4️⃣ 400 m/s
✔️ Answer: 540 m/s
📘 Exam: JEE Advanced 2010 (Paper 2)

🔴 Question 33:
In kinetic theory, gas molecules are considered
🟢 1️⃣ Point masses with elastic collisions
🔵 2️⃣ Extended masses with friction
🟡 3️⃣ Charged particles
🟣 4️⃣ With intermolecular forces
✔️ Answer: Point masses with elastic collisions
📘 Exam: JEE Advanced 2009 (Paper 2)

🔴 Question 34:
The ratio of rms velocity to most probable velocity is
🟢 1️⃣ √(3/2)
🔵 2️⃣ √(2/3)
🟡 3️⃣ 1
🟣 4️⃣ √(π/2)
✔️ Answer: √(3/2)
📘 Exam: JEE Advanced 2008 (Paper 2)

PRACTICE SETS FROM THIS LESSON

🔹 NEET Level (Q1–Q20)
Q1. The pressure exerted by a gas is due to
🔵(A) random motion of molecules
🟢(B) attraction between molecules
🟠(C) collisions of molecules with container walls
🔴(D) gravity of molecules
Answer: (C) collisions of molecules with container walls

Q2. The mean kinetic energy of a molecule of an ideal gas is
🔵(A) proportional to pressure
🟢(B) proportional to temperature
🟠(C) proportional to volume
🔴(D) independent of temperature
Answer: (B) proportional to temperature

Q3. The root mean square speed of molecules is given by
🔵(A) √(3RT/M)
🟢(B) √(2RT/M)
🟠(C) √(RT/M)
🔴(D) √(8RT/πM)
Answer: (A) √(3RT/M)

Q4. The average speed of oxygen molecules at 300 K is approximately
🔵(A) 350 m/s
🟢(B) 420 m/s
🟠(C) 450 m/s
🔴(D) 480 m/s
Answer: (D) 480 m/s

Q5. Which quantity is same for all gases at the same temperature?
🔵(A) rms speed
🟢(B) kinetic energy
🟠(C) pressure
🔴(D) density
Answer: (B) kinetic energy

Q6. For an ideal gas, if the temperature is doubled at constant pressure, then average speed of molecules becomes
🔵(A) double
🟢(B) half
🟠(C) √2 times
🔴(D) 4 times
Answer: (C) √2 times

Q7. The ratio of most probable speed to rms speed is
🔵(A) 1.00
🟢(B) 1.08
🟠(C) 1.22
🔴(D) 0.816
Answer: (D) 0.816

Q8. The Boltzmann constant (k) is defined as
🔵(A) k = R × N_A
🟢(B) k = R / N_A
🟠(C) k = N_A / R
🔴(D) k = 1 / R
Answer: (B) k = R / N_A

Q9. The pressure exerted by 1 mol of gas at 27°C in 22.4 L volume is
🔵(A) 1 atm
🟢(B) 0.5 atm
🟠(C) 2 atm
🔴(D) 4 atm
Answer: (A) 1 atm

Q10. The rms speed of gas molecules depends on
🔵(A) temperature only
🟢(B) molecular mass only
🟠(C) both temperature and molecular mass
🔴(D) pressure
Answer: (C) both temperature and molecular mass

Q11. At 0°C, the ratio of rms speeds of H₂ and O₂ is
🔵(A) 1
🟢(B) 4
🟠(C) 1/4
🔴(D) 8
Answer: (B) 4

Q12. The mean free path of a gas molecule is inversely proportional to
🔵(A) pressure
🟢(B) temperature
🟠(C) volume
🔴(D) molecular velocity
Answer: (A) pressure

Q13. The gas constant R has units
🔵(A) J mol⁻¹ K⁻¹
🟢(B) J K mol⁻¹
🟠(C) N m mol⁻¹
🔴(D) kg m² s⁻²
Answer: (A) J mol⁻¹ K⁻¹

Q14. Which of the following assumptions is not made in kinetic theory?
🔵(A) Molecules are in random motion
🟢(B) Collisions are elastic
🟠(C) Molecular volume is negligible
🔴(D) Molecules exert strong forces on each other
Answer: (D) Molecules exert strong forces on each other

Q15. The average translational kinetic energy of one mole of gas molecules is
🔵(A) RT
🟢(B) (3/2)RT
🟠(C) (1/2)RT
🔴(D) 2RT
Answer: (B) (3/2)RT

Q16. The speed of sound in a gas is related to its
🔵(A) C_p
🟢(B) C_v
🟠(C) γ
🔴(D) temperature
Answer: (C) γ

Q17. The ratio of degrees of freedom for diatomic and monoatomic gases is
🔵(A) 3/5
🟢(B) 5/3
🟠(C) 2
🔴(D) 1
Answer: (B) 5/3

Q18. The molecular velocity distribution curve shifts right when
🔵(A) temperature increases
🟢(B) pressure increases
🟠(C) gas cools
🔴(D) molecular mass increases
Answer: (A) temperature increases

Q19. At constant pressure, if temperature is doubled, rms speed changes by
🔵(A) √2
🟢(B) 2
🟠(C) 1/2
🔴(D) 4
Answer: (A) √2

Q20. The number of degrees of freedom of an argon atom is
🔵(A) 2
🟢(B) 3
🟠(C) 5
🔴(D) 6
Answer: (B) 3

🔹 JEE Main Level (Q21–Q40)
Q21. The energy of 1 mole of an ideal monoatomic gas at 27°C is
🔵(A) (3/2)RT
🟢(B) (5/2)RT
🟠(C) (7/2)RT
🔴(D) 3RT
Answer: (A) (3/2)RT

Q22. For a diatomic gas, ratio C_p:C_v is
🔵(A) 7:5
🟢(B) 5:3
🟠(C) 3:2
🔴(D) 4:3
Answer: (A) 7:5

Q23. The root mean square speed of a gas molecule at temperature T is proportional to
🔵(A) T
🟢(B) √T
🟠(C) 1/T
🔴(D) 1/√T
Answer: (B) √T

Q24. If the temperature of a gas becomes 9 times its initial value, the rms speed becomes
🔵(A) 3 times
🟢(B) 9 times
🟠(C) 81 times
🔴(D) unchanged
Answer: (A) 3 times

Q25. In kinetic theory, the expression for pressure can be written as
🔵(A) P = (1/3)ρv²
🟢(B) P = (1/2)ρv²
🟠(C) P = (1/4)ρv²
🔴(D) P = ρv²
Answer: (A) P = (1/3)ρv²

Q26. The number of molecules in 1 mole of a gas is
🔵(A) 6.023 × 10²³
🟢(B) 3 × 10⁸
🟠(C) 10²⁴
🔴(D) 1 × 10⁶
Answer: (A) 6.023 × 10²³

Q27. The translational kinetic energy per unit volume of an ideal gas is
🔵(A) (3/2)P
🟢(B) (1/2)P
🟠(C) (2/3)P
🔴(D) (P/3)
Answer: (A) (3/2)P

Q28. The relation between average speed vₐᵥg and rms speed vᵣₘₛ is
🔵(A) vᵣₘₛ = 1.08 vₐᵥg
🟢(B) vₐᵥg = 1.08 vᵣₘₛ
🟠(C) vₐᵥg = 0.707 vᵣₘₛ
🔴(D) vₐᵥg = 1.22 vᵣₘₛ
Answer: (A) vᵣₘₛ = 1.08 vₐᵥg

Q29. A gas molecule moving with speed v strikes the wall. The pressure is proportional to
🔵(A) v
🟢(B) v²
🟠(C) 1/v
🔴(D) √v
Answer: (B) v²

Q30. The temperature at which the rms speed of O₂ molecules is double that at 300 K is
🔵(A) 600 K
🟢(B) 900 K
🟠(C) 1200 K
🔴(D) 1500 K
Answer: (B) 1200 K

Q31. The equation connecting P, V, and T for an ideal gas is derived from
🔵(A) Boyle’s law
🟢(B) Charles’ law
🟠(C) Avogadro’s law
🔴(D) kinetic theory
Answer: (D) kinetic theory

Q32. For a monoatomic gas, C_p =
🔵(A) (3/2)R
🟢(B) (5/2)R
🟠(C) (7/2)R
🔴(D) R
Answer: (B) (5/2)R

Q33. The mean free path of a gas molecule is inversely proportional to
🔵(A) T
🟢(B) √T
🟠(C) n
🔴(D) 1/n
Answer: (C) n

Q34. The kinetic energy of 1 mol of an ideal gas at 27°C is approximately
🔵(A) 3.74 kJ
🟢(B) 4.16 kJ
🟠(C) 2.50 kJ
🔴(D) 1.50 kJ
Answer: (B) 4.16 kJ

Q35. If two gases have same temperature, then their molecules have
🔵(A) same rms speed
🟢(B) same average kinetic energy
🟠(C) same momentum
🔴(D) same density
Answer: (B) same average kinetic energy

Q36. The total translational energy of 3 moles of gas at 300 K is
🔵(A) 3 × (3/2)RT
🟢(B) (3/2)RT
🟠(C) 9RT
🔴(D) 4.5RT
Answer: (A) 3 × (3/2)RT

Q37. The value of γ for triatomic gas is
🔵(A) 1.67
🟢(B) 1.4
🟠(C) 1.33
🔴(D) 1.2
Answer: (C) 1.33

Q38. The most probable speed corresponds to
🔵(A) maximum fraction of molecules
🟢(B) average speed
🟠(C) maximum kinetic energy
🔴(D) all molecules
Answer: (A) maximum fraction of molecules

Q39. The root mean square velocity of nitrogen molecules at 0°C is about
🔵(A) 200 m/s
🟢(B) 400 m/s
🟠(C) 500 m/s
🔴(D) 517 m/s
Answer: (D) 517 m/s

Q40. The pressure due to gas molecules striking per unit area is proportional to
🔵(A) average velocity
🟢(B) square of rms speed
🟠(C) temperature
🔴(D) volume
Answer: (B) square of rms speed

🔹 JEE Advanced Level (Q41–Q50)
Q41. The kinetic interpretation of temperature fails at
🔵(A) low temperatures
🟢(B) high pressures
🟠(C) near absolute zero
🔴(D) ideal conditions
Answer: (C) near absolute zero

Q42. If two gases at same temperature have molecular masses M₁ and M₂, the ratio of their rms speeds is
🔵(A) √(M₂/M₁)
🟢(B) √(M₁/M₂)
🟠(C) (M₁/M₂)
🔴(D) (M₂/M₁)
Answer: (A) √(M₂/M₁)

Q43. The internal energy of 2 moles of a monoatomic gas at 27°C is
🔵(A) 3RT
🟢(B) (3/2) × 2RT
🟠(C) (5/2) × 2RT
🔴(D) 4RT
Answer: (B) (3/2) × 2RT

Q44. The rms speed of CO₂ at 0°C is approximately
🔵(A) 300 m/s
🟢(B) 400 m/s
🟠(C) 500 m/s
🔴(D) 600 m/s
Answer: (A) 300 m/s

Q45. At what temperature will the rms speed of N₂ be 600 m/s? (M = 28×10⁻³ kg mol⁻¹)
🔵(A) 300 K
🟢(B) 400 K
🟠(C) 480 K
🔴(D) 500 K
Answer: (C) 480 K

Q46. A gas has γ = 1.67. It must be
🔵(A) monoatomic
🟢(B) diatomic
🟠(C) polyatomic
🔴(D) vapour
Answer: (A) monoatomic

Q47. When temperature increases, mean free path increases because
🔵(A) molecular size increases
🟢(B) density decreases
🟠(C) collision frequency decreases
🔴(D) molecular mass increases
Answer: (B) density decreases

Q48. If the temperature of 1 mol of gas increases by 10 K, then change in kinetic energy is
🔵(A) 3R × 10
🟢(B) (3/2)R × 10
🟠(C) 5R × 10
🔴(D) R × 10
Answer: (B) (3/2)R × 10

Q49. The pressure exerted by a gas kept in a vessel is due to
🔵(A) gravitational force
🟢(B) electrostatic attraction
🟠(C) molecular collisions with walls
🔴(D) cohesive forces
Answer: (C) molecular collisions with walls

Q50. Which of the following statements is correct for kinetic theory?
🔵(A) It neglects molecular motion
🟢(B) It assumes elastic collisions
🟠(C) It considers potential energy of interaction
🔴(D) It ignores translational motion
Answer: (B) It assumes elastic collisions

Important Notice : The lessons and study materials up to July–August 2025 have been sent. Soon, after receiving feedback from teachers and students, we will deliver the latest and more innovative study materials for the upcoming months.