Class 11 : Physics (In English) – Chapter 3: Motion in a Plane
EXPLANATION & SUMMARY
🔵 Explanation
🌿 Introduction
Motion in a plane involves the movement of an object in two dimensions (2D), meaning the object changes position along both x-axis and y-axis simultaneously. Such motion is described using vector quantities because both magnitude and direction are important.
Examples include:
🟢 A ball thrown at an angle (projectile motion)
🔵 A car turning on a curved road
🔴 The motion of planets around the Sun
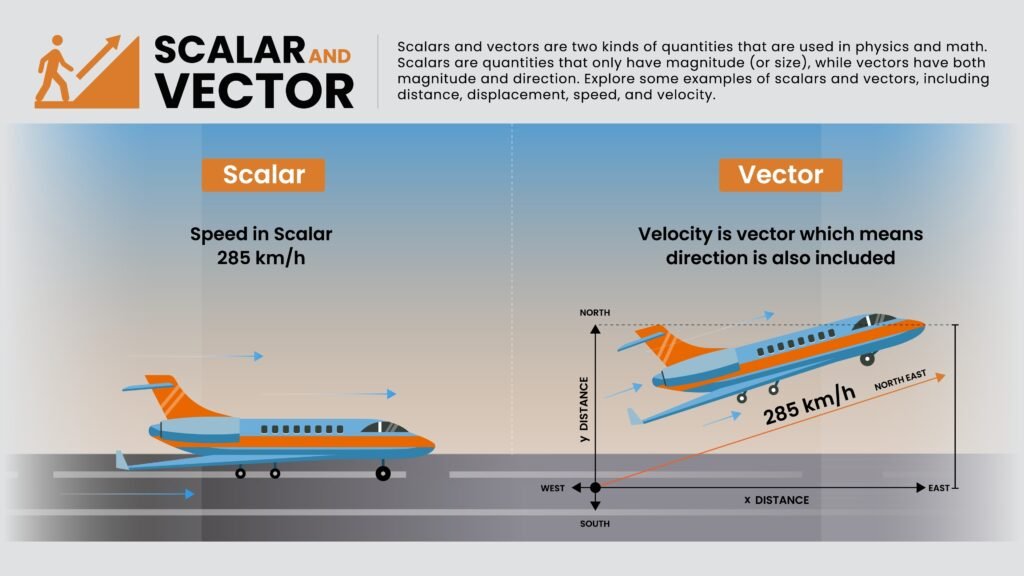
💡 Concept: Scalar and Vector Quantities
✏️ Scalar Quantities → Have only magnitude (e.g., mass, speed, time, energy).
✏️ Vector Quantities → Have both magnitude and direction (e.g., displacement, velocity, acceleration, force).
Vectors are represented by arrows; the length shows magnitude, and the arrowhead shows direction.
⚡ Vector Representation and Notation
Let vector A be represented as
➡️ A = Aₓ î + Aᵧ ĵ
where,
🔵 Aₓ = component of vector along x-axis
🟢 Aᵧ = component of vector along y-axis
and the magnitude |A| = √(Aₓ² + Aᵧ²).
The direction θ = tan⁻¹(Aᵧ / Aₓ).

🧠 Vector Addition and Subtraction
When two vectors act on the same point, they can be added using either the Triangle Law or the Parallelogram Law.
➤ Triangle Law of Vector Addition
If vectors A and B are represented as two sides of a triangle taken in order, then the resultant vector R is represented by the third side taken in the opposite order.
Formula:
R = √(A² + B² + 2AB cos θ)
Direction: tan α = (B sin θ) / (A + B cos θ)

➤ Parallelogram Law
If two vectors act simultaneously at a point and are represented by the two adjacent sides of a parallelogram, the diagonal passing through that point gives the resultant.
🔴 Vector Subtraction
To subtract vector B from vector A, we add A + (−B), where −B is the vector equal in magnitude but opposite in direction to B.
🟡 Multiplication of a Vector by a Scalar
If a vector A is multiplied by a real number n:
➡️ Resultant vector R = nA
• If n > 0 → Direction remains same
• If n < 0 → Direction reverses
• Magnitude changes by |n|
💡 Position and Displacement Vectors
The position vector of a point P(x, y) is:
➡️ r = x î + y ĵ
If a particle moves from P(x₁, y₁) to Q(x₂, y₂), then
➡️ Displacement vector = r₂ − r₁ = (x₂ − x₁) î + (y₂ − y₁) ĵ
🌿 Velocity and Acceleration Vectors
✔️ Average velocity = (r₂ − r₁) / (t₂ − t₁)
✔️ Instantaneous velocity = dr/dt
✔️ Average acceleration = (v₂ − v₁) / (t₂ − t₁)
✔️ Instantaneous acceleration = dv/dt
All these are vector quantities.
⚡ Projectile Motion
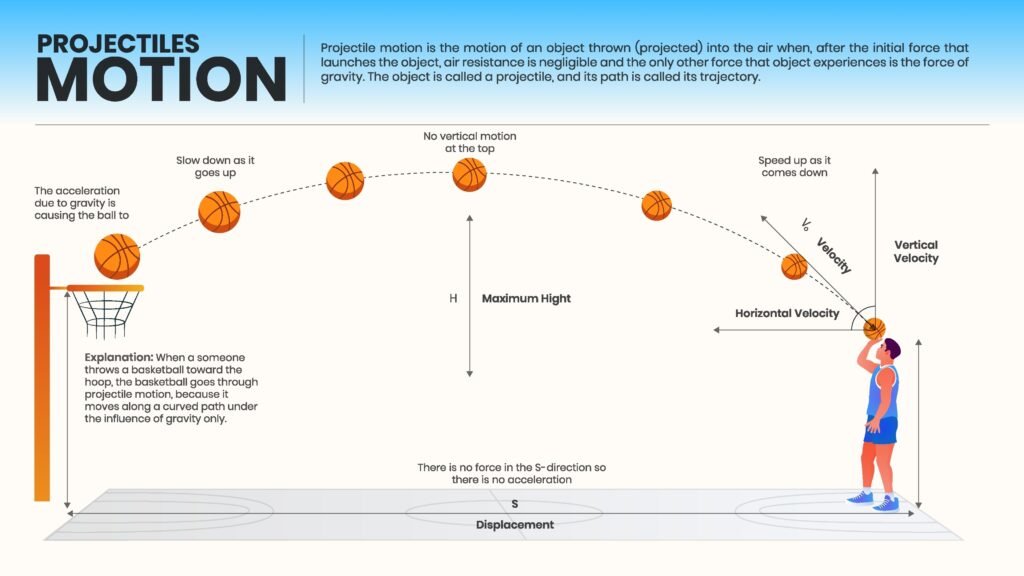
When a body is thrown with an initial velocity u making an angle θ with the horizontal, it follows a parabolic path.
Let:
🟢 Horizontal velocity = uₓ = u cos θ
🔵 Vertical velocity = uᵧ = u sin θ
Then,
• Time of flight: T = (2u sin θ) / g
• Maximum height: H = (u² sin² θ) / (2g)
• Horizontal range: R = (u² sin 2θ) / g
• Equation of trajectory: y = x tan θ − (g x²) / (2u² cos² θ)
🧠 The maximum range occurs when θ = 45°.
💡 Relative Velocity in Two Dimensions
If two objects A and B move with velocities vₐ and vᵦ,
➡️ Relative velocity of A w.r.t B = vₐᵦ = vₐ − vᵦ
Example:
An airplane flying in wind experiences a resultant velocity which is the vector sum of its own velocity and that of the wind.
🌿 Uniform Circular Motion
When an object moves in a circle at constant speed, its direction continuously changes — hence, its velocity vector changes even though speed remains constant.
For an object of mass m moving in a circle of radius r with speed v:
➡️ Centripetal acceleration a = v² / r
➡️ Centripetal force F = mv² / r
This force always acts towards the center.
⚡ Important Concepts Recap
✔️ Motion in a plane involves two independent perpendicular directions.
✔️ Vector addition follows laws of triangle or parallelogram.
✔️ Projectile motion combines uniform motion in x-direction and uniformly accelerated motion in y-direction.
✔️ Centripetal acceleration is always directed toward the center of the circular path.
🟢 Summary (≈300 words)
🧠 Motion in a plane involves describing motion using vectors in two dimensions. A vector has magnitude and direction, unlike a scalar which has only magnitude. Vectors are represented using unit vectors î, ĵ, and k̂ for the x, y, and z directions respectively.
Vector addition can be done using triangle or parallelogram laws. The resultant vector’s magnitude and direction depend on the angle between the two vectors. Subtraction is performed by adding the negative of one vector to another. Multiplying a vector by a scalar affects only its magnitude, not its direction unless the scalar is negative.
Position and displacement vectors describe the movement of particles between two points. Velocity and acceleration vectors express how position and velocity change with time.
Projectile motion combines horizontal uniform motion and vertical uniformly accelerated motion due to gravity. The path of a projectile is parabolic, with time of flight, maximum height, and range determined by initial velocity and angle of projection.
Relative velocity explains how motion appears to one moving object when compared to another. In uniform circular motion, an object experiences centripetal acceleration and force directed toward the center, even though its speed remains constant.
📝 Quick Recap
🔵 Motion in a plane → 2D motion involving vectors.
🟢 Laws of vector addition → Triangle & Parallelogram.
🟠 Projectile motion → Parabolic path; maximum range at 45°.
🔴 Centripetal acceleration → v² / r, acts toward center.
💡 Relative velocity → Difference of two velocity vectors
————————————————————————————————————————————————————————————————————————————
QUESTIONS FROM TEXTBOOK
Question
3.1 State, for each of the following physical quantities, if it is a scalar or a vector: volume, mass, speed, acceleration, density, number of moles, velocity, angular frequency, displacement, angular velocity.
Answer
🔵 Classification (with brief reasons):
➡️ Volume → Scalar (magnitude only)
➡️ Mass → Scalar (magnitude only)
➡️ Speed → Scalar (rate of distance change; no direction)
➡️ Acceleration → Vector (change of velocity has direction)
➡️ Density → Scalar (mass per unit volume; magnitude only)
➡️ Number of moles → Scalar (count of entities)
➡️ Velocity → Vector (rate of displacement; direction essential)
➡️ Angular frequency (ω) → Scalar (magnitude of angular rate; direction not included)
➡️ Displacement → Vector (directed distance)
➡️ Angular velocity (⃗ω) → Vector (direction given by right-hand rule)
✏️ Note: The magnitude of a vector is a scalar; the vector itself carries direction.
Question
3.2 Pick out the two scalar quantities in the following list: force, angular momentum, work, current, linear momentum, electric field, average velocity, magnetic moment, relative velocity.
Answer
🧠 Check each:
✔️ Force → vector
✔️ Angular momentum → vector
✔️ Work → scalar
✔️ Current → scalar (electric current is scalar under rotation)
✔️ Linear momentum → vector
✔️ Electric field → vector
✔️ Average velocity → vector
✔️ Magnetic moment → vector (axial vector)
✔️ Relative velocity → vector
🔴 Therefore, the two scalars are: Work and Current.
Question
3.3 Pick out the only vector quantity in the following list: Temperature, pressure, impulse, time, power, total path length, energy, gravitational potential, coefficient of friction, charge.
Answer
🧠 Check each:
➡️ Temperature → scalar
➡️ Pressure → scalar
➡️ Impulse → vector (Δ⃗p)
➡️ Time → scalar
➡️ Power → scalar
➡️ Total path length → scalar
➡️ Energy → scalar
➡️ Gravitational potential → scalar
➡️ Coefficient of friction → scalar
➡️ Charge → scalar
✔️ The only vector quantity is Impulse.
Question
3.4 State with reasons, whether the following algebraic operations with scalar and vector physical quantities are meaningful:
(a) adding any two scalars, (b) adding a scalar to a vector of the same dimensions, (c) multiplying any vector by any scalar, (d) multiplying any two scalars, (e) adding any two vectors, (f) adding a component of a vector to the same vector.
Answer
(a) 🔵 Adding any two scalars → Not meaningful in general.
➡️ ✔️ Meaningful only when they represent the same physical quantity/units (e.g., 3 kg + 2 kg).
➡️ ✖️ Not meaningful for unlike quantities (e.g., 3 kg + 2 m).
(b) 🟢 Adding a scalar to a vector of the same dimensions → Not meaningful.
➡️ Vector addition requires vector + vector; a scalar lacks direction.
(c) 🟠 Multiplying any vector by any scalar → Meaningful.
➡️ Result is a vector in the same or opposite direction depending on the sign of the scalar; magnitude scales by the scalar factor.
➡️ Units change if the scalar is dimensional.
(d) 🔴 Multiplying any two scalars → Meaningful.
➡️ Result is a scalar with product units (e.g., work = force magnitude * displacement along direction).
(e) 🔵 Adding any two vectors → Meaningful only if they are of the same physical kind (same dimensions/units).
➡️ E.g., velocity + velocity is defined; force + displacement is not.
(f) 🟢 Adding a component of a vector to the same vector → Meaningful.
➡️ The component (e.g., A_x î) is itself a vector; A + A_x î is a valid vector sum (same dimensions).
Question
🔹 Question 3.5
Read each statement carefully and state with reasons, if it is true or false:
(a) The magnitude of a vector is always a scalar.
(b) Each component of a vector is always a scalar.
(c) The total path length is always equal to the magnitude of the displacement vector of a particle.
(d) The average speed of a particle (defined as total path length divided by time taken) is either greater or equal to the magnitude of average velocity of the particle over the same interval of time.
(e) Three vectors not lying in a plane can never add up to give a null vector.
✏️ Answer:
🔵 (a) True
💡 The magnitude of a vector gives only its size, not direction, so it is a scalar.
Example: The magnitude of velocity (|v|) represents speed, which is scalar.
🟢 (b) False
💡 Each component of a vector (like Vₓ or Vᵧ) is directional along its axis.
Though it is represented by a number, it behaves as a vector quantity in that direction.
🟠 (c) False
💡 The total path length = actual distance travelled.
Displacement = shortest distance between initial and final positions.
They are equal only for straight-line motion without a change in direction, otherwise
Total path length > |displacement|.
🔴 (d) True
💡 Average speed = (Total path length / Time)
Average velocity = (Displacement / Time)
Since total path ≥ displacement, average speed ≥ magnitude of average velocity.
They are equal only for straight-line motion.
🟣 (e) True
💡 For three vectors to give a null (zero) resultant, they must form a closed triangle — hence they must lie in the same plane.
If they don’t lie in one plane, they can never form a closed figure.
✅ Final Answers Summary:
(a) True (b) False (c) False (d) True (e) True
🔹 Question 3.6
Establish the following vector inequalities geometrically or otherwise:
(a) |a + b| ≤ |a| + |b|
(b) |a + b| ≥ ||a| − |b||
(c) |a − b| ≤ |a| + |b|
(d) |a − b| ≥ ||a| − |b||
Also state when the equality sign holds true.
✏️ Answer:
💡 Using triangle law of vector addition:
If two vectors a and b are represented as adjacent sides of a triangle,
then their resultant a + b is the third side of the triangle.
From the triangle property:
➡️ (a) |a + b| ≤ |a| + |b|
✔️ Equality holds when a and b are in the same direction (θ = 0°).
➡️ (b) |a + b| ≥ ||a| − |b||
✔️ Equality holds when a and b are in opposite directions (θ = 180°).
Similarly, for a − b (which is same as a + (−b)):
➡️ (c) |a − b| ≤ |a| + |b|
✔️ Equality holds when a and (−b) are in the same direction (θ = 0°).
➡️ (d) |a − b| ≥ ||a| − |b||
✔️ Equality holds when a and b are in the same or opposite directions.
💡 Geometrical Meaning:
These inequalities express the triangle inequalities —
the length of one side of a triangle is always less than or equal to the sum of the other two sides
and greater than or equal to their difference.
✅ Equality Condition Summary:
|a + b| = |a| + |b| → when a ∥ b (same direction)
|a + b| = ||a| − |b|| → when a ∥ b (opposite direction)
|a − b| = |a| + |b| → when a ∥ −b
|a − b| = ||a| − |b|| → when a ∥ b
🔷 Question 3.7
Given that a + b + c + d = 0, which of the following statements are correct?
(a) a, b, c, and d must each be a null vector.
(b) The magnitude of (a + c) equals the magnitude of (b + d).
(c) The magnitude of a can never be greater than the sum of the magnitudes of b, c, and d.
(d) b + c must lie in the plane of a and d if a and d are not collinear, and in the line of a and d if they are collinear.
Answer
(a) a, b, c, d must each be a null vector.
❌ False
Reason: Many non-zero vectors can add to zero (closed polygon). So none need be null individually.
(b) |a + c| equals |b + d|.
✔️ True
Reason: From a + b + c + d = 0 ⇒ a + c = −(b + d). Taking magnitudes: |a + c| = |−(b + d)| = |b + d|.
(c) |a| can never be greater than the sum of |b|, |c|, |d|.
✔️ True
Reason: a = −(b + c + d) ⇒ |a| = |b + c + d| ≤ |b| + |c| + |d| (triangle inequality).
(d) b + c must lie in the plane of a and d if a and d are not collinear, and in the line of a and d if they are collinear.
✔️ True
Reason: b + c = −(a + d). Hence b + c is collinear with a + d.
If a and d are not collinear, a + d lies in the plane spanned by a and d ⇒ b + c lies in the same plane.
If a and d are collinear, a + d lies along that line ⇒ b + c lies along the same line.
✅ Correct options: (b), (c), (d).
Question 3.8
Three girls skating on a circular ice ground of radius 200 m start from a point P on the edge of the ground and reach a point Q diametrically opposite to P following different paths.
(a) What is the magnitude of the displacement vector for each?
(b) For which girl is this equal to the actual length of the path skated?
Answer
🧠 Given: The circle has radius r = 200 m.
From geometry, P and Q are diametrically opposite, so the displacement is the diameter.
➡️ (a) Displacement = PQ = 2r = 2 × 200 = 400 m
➡️ (b) For the girl skating along the diameter (straight path),
Displacement = path length = 400 m.
✔️ Hence,
(a) Displacement = 400 m for all three.
(b) Only the girl skating along the straight line PQ has displacement equal to path length.
Question 3.9
A cyclist starts from the centre O of a circular park of radius 1 km, reaches the edge P of the park, then cycles along the circumference, and returns to the centre along QO as shown in Fig. 3.20.
If the round trip takes 10 min, what is the
(a) net displacement,
(b) average velocity, and
(c) average speed of the cyclist?
Answer
Given:
Radius, r = 1 km
Time taken, t = 10 min = 600 s
Path: O → P → Q → O
✔️ The path forms a semicircle PQ + two radii.
(a) Net displacement:
Cyclist returns to O (initial point).
So, displacement = 0
(b) Average velocity:
v_avg = Displacement / Time = 0 / 600 = 0
(c) Average speed:
Path length = OP + arc PQ + QO
= r + (πr) + r = (2 + π)r
Substitute r = 1 km
= (2 + 3.14) × 1 = 5.14 km
Average speed = Total path / Total time
= 5.14 km / (10/60 h) = 5.14 × 6 = 30.84 km h⁻¹
✅ Final answers:
(a) 0 km
(b) 0 km h⁻¹
(c) 30.84 km h⁻¹
Question 3.10
On an open ground, a motorist follows a track that turns to his left by an angle of 60° after every 500 m. Starting from a given turn, specify the displacement of the motorist at the third, sixth, and eighth turn. Compare the magnitude of the displacement with the total path length covered by the motorist in each case.
Answer
💡 Each side of the path = 500 m, turning left by 60° each time.
After 6 turns, the direction completes 360°, so the motorist returns to the starting point.
➡️ Third turn:
Forms an equilateral triangle with side 500 m.
Hence displacement = 500 m (closing side of triangle).
Total path length = 3 × 500 = 1500 m.
➡️ Sixth turn:
Motorist returns to start.
So, displacement = 0, path = 6 × 500 = 3000 m.
➡️ Eighth turn:
Equivalent to two extra sides beyond a full hexagon → forms an equilateral triangle again.
Displacement = 500 m, path = 8 × 500 = 4000 m.
✅ Summary:
3rd turn → displacement = 500 m
6th turn → displacement = 0
8th turn → displacement = 500 m
Question 3.11
A passenger arriving in a new town wishes to go from the station to a hotel located 10 km away on a straight road from the station.
A dishonest cabman takes him along a circuitous path 23 km long and reaches the hotel in 28 min.
What is
(a) the average speed of the taxi,
(b) the magnitude of average velocity? Are the two equal?
Answer
Given:
Path = 23 km,
Displacement = 10 km,
Time = 28 min = 28/60 h = 0.467 h
➡️ (a) Average speed = Total path / Time
= 23 / 0.467 = 49.25 km h⁻¹
➡️ (b) Average velocity = Displacement / Time
= 10 / 0.467 = 21.4 km h⁻¹
✔️ Not equal because path ≠ displacement.
Average speed > Average velocity.
✅ Final answers:
(a) 49.25 km h⁻¹
(b) 21.4 km h⁻¹
Question 3.12
The ceiling of a long hall is 25 m high.
What is the maximum horizontal distance that a ball thrown with a speed of 40 m s⁻¹ can go without hitting the ceiling of the hall?
Answer
Given:
u = 40 m s⁻¹, h_max = 25 m, g = 9.8 m s⁻²
For projectile,
h_max = (u² sin²θ) / (2g)
➡️ 25 = (40² sin²θ) / (2 × 9.8)
⇒ sin²θ = (25 × 19.6) / 1600 = 0.30625
⇒ sinθ = 0.553
➡️ θ = 33.6°
Horizontal range: R = (u² sin2θ) / g
= (1600 × sin67.2°) / 9.8
= (1600 × 0.923) / 9.8 = 150.8 m
✅ Maximum horizontal distance without touching ceiling = ≈150.8 m
Question 3.13
A cricketer can throw a ball to a maximum horizontal distance of 100 m.
How much high above the ground can the cricketer throw the same ball?
Answer
💡 Maximum range (R_max) is achieved at θ = 45°.
Range R_max = (u² sin2θ) / g = (u²) / g
➡️ Given R_max = 100 ⇒ u² = 100g
Maximum height (H_max) = (u² sin²θ) / (2g)
At θ = 45°, sin²45° = (1/2)
➡️ H_max = (100g × 1/2) / (2g) = 25 m
✅ The ball can reach 25 m high above the ground.
Question 3.14
A stone tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolutions in 25 s, what is the magnitude and direction of acceleration of the stone?
Answer
🔹 Given: r = 0.80 m, N = 14 revolutions, t = 25 s
➡️ Frequency, f = N / t = 14 / 25 = 0.56 s⁻¹
➡️ Angular speed, ω = 2πf = 2π × 0.56 = 3.52 rad s⁻¹
➡️ Centripetal acceleration, a_c = ω²r
= (3.52)² × 0.80
= 9.9 m s⁻²
✔️ Magnitude: a_c = 9.9 m s⁻²
✔️ Direction: Towards the centre of the circular path (radially inward).
Question 3.15
An aircraft executes a horizontal loop of radius 1.00 km with a steady speed of 900 km h⁻¹. Compare its centripetal acceleration with the acceleration due to gravity.
Answer
🔹 Given: r = 1 km = 1000 m, v = 900 km h⁻¹ = (900×1000)/3600 = 250 m s⁻¹
➡️ a_c = v² / r = (250)² / 1000 = 62.5 m s⁻²
➡️ a_c / g = 62.5 / 9.8 = 6.38 ≈ 6.4
✔️ Centripetal acceleration = 6.4 g, directed horizontally towards the centre of the loop.
Question 3.16
Read each statement below carefully and state, with reasons, if it is true or false:
(a) The net acceleration of a particle in circular motion is always along the radius of the circle towards the centre.
(b) The velocity vector of a particle at a point is always along the tangent to the path at that point.
(c) The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector.
Answer
(a) ❌ False — In non-uniform circular motion, acceleration has both radial and tangential components; the net acceleration is not purely radial.
(b) ✔️ True — The instantaneous velocity vector is always tangential to the trajectory.
(c) ✔️ True — In uniform circular motion, acceleration continuously changes direction and its average over one revolution = 0.
Question 3.17
The position of a particle is given by
⃗r = 3.0t î − 2.0t² ĵ + 4.0k̂ (in metres).
Find (a) velocity ⃗v and acceleration ⃗a, and (b) the magnitude and direction of velocity at t = 2.0 s.
Answer
➡️ (a) Velocity, ⃗v = d⃗r/dt = 3.0 î − 4.0t ĵ + 0k̂
➡️ Acceleration, ⃗a = d⃗v/dt = 0 î − 4.0 ĵ + 0k̂
At t = 2 s:
➡️ ⃗v = 3 î − 8 ĵ (m s⁻¹)
➡️ |⃗v| = (3² + (−8)²)^(1/2) = (73)^(1/2) = 8.54 m s⁻¹
Direction:
tanθ = |v_y| / v_x = 8 / 3 ⇒ θ = 69.4° below +x-axis.
✔️ v = 8.54 m s⁻¹, direction 69.4° below +x-axis.
Question 3.18
A particle starts from the origin at t = 0 with velocity 10 ĵ m s⁻¹ and moves in the x–y plane with constant acceleration (8 î + 2 ĵ) m s⁻².
(a) At what time is x = 16 m?
(b) What is y at that time?
(c) What is the speed of the particle then?
Answer
Given:
⃗v₀ = (0, 10), ⃗a = (8, 2)
(a) x = ½ aₓt² ⇒ 16 = 4t² ⇒ t² = 4 ⇒ t = 2 s
(b) y = v₀y t + ½ a_y t²
= 10×2 + 1×(2²) = 20 + 4 = 24 m
(c) ⃗v = ⃗v₀ + ⃗a t = (0 + 8×2) î + (10 + 2×2) ĵ = (16 î + 14 ĵ)
➡️ Speed = (16² + 14²)^(1/2) = (452)^(1/2) = 21.3 m s⁻¹
✔️ Answers:
t = 2 s, y = 24 m, v = 21.3 m s⁻¹
Question 3.19
î and ĵ are unit vectors along x and y axes respectively.
(a) Find magnitude and direction of (î + ĵ) and (î − ĵ).
(b) Find components of ⃗A = 2 î + 3 ĵ along (î + ĵ) and (î − ĵ).
Answer
(a) |î + ĵ| = (1² + 1²)^(1/2) = √2 → 45° above +x-axis
|î − ĵ| = (1² + (−1)²)^(1/2) = √2 → 45° below +x-axis
(b) Unit directions:
û₁ = (î + ĵ)/√2 , û₂ = (î − ĵ)/√2
A₁ = ⃗A·û₁ = (2×1 + 3×1)/√2 = 5/√2
A₂ = ⃗A·û₂ = (2×1 + 3×(−1))/√2 = −1/√2
✔️ Components along (î + ĵ) and (î − ĵ): 5/√2, −1/√2
Question 3.20
For arbitrary motion in space, which of the following relations are true?
(a) ⃗v_avg = ½[⃗v(t₁) + ⃗v(t₂)]
(b) ⃗v_avg = [⃗r(t₂) − ⃗r(t₁)] / (t₂ − t₁)
(c) ⃗v(t) = ⃗v(0) + ⃗a t
(d) ⃗r(t) = ⃗r(0) + ⃗v(0)t + ½⃗a t²
(e) ⃗a_avg = [⃗v(t₂) − ⃗v(t₁)] / (t₂ − t₁)
Answer
✔️ True → (b), (e) (valid for all motion types).
✖️ False → (a), (c), (d) (only true for constant acceleration).
Question 3.21
Read each statement carefully and state if true or false with reasons:
(a) A scalar quantity is one that is conserved in a process.
(b) A scalar can never take negative values.
(c) A scalar quantity must be dimensionless.
(d) A scalar does not vary from point to point in space.
(e) A scalar has the same value for observers with different orientations of axes.
Answer
(a) ✖️ False — “Scalar” means no direction; conservation is unrelated.
(b) ✖️ False — Scalars can be negative (work, potential).
(c) ✖️ False — Scalars may have dimensions (mass, time).
(d) ✖️ False — Scalars can vary spatially (temperature).
(e) ✔️ True — Scalars are invariant under rotation.
Question 3.22
An aircraft flies at a height of 3400 m. If the angle subtended at a ground point by aircraft positions 10.0 s apart is 30°, what is its speed?
Answer
✏️ Let the aircraft move horizontally at height h = 3400 m, subtending total angle 2θ = 30°, so θ = 15°.
➡️ tanθ = (v × 5) / h
v = h tanθ / 5 = (3400 × tan15°)/5
tan15° = 0.2679
v = (3400 × 0.2679)/5 = 182 m s⁻¹ = 182×3.6 = 656 km h⁻¹
✔️ Speed = 1.82×10² m s⁻¹ ≈ 6.56×10² km h⁻¹
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS FOR EXAMS
(CBSE MODEL QUESTIONS PAPER)
ESPECIALLY MADE FROM THIS LESSON ONLY
🔵 SECTION A – (Q1–Q18: Multiple Choice Questions)
Question 1.
A quantity that has both magnitude and direction is known as:
🔵 (A) Scalar
🟢 (B) Vector
🟠 (C) Quantity
🔴 (D) Constant
Answer: (B) Vector
Question 2.
The magnitude of the resultant of two vectors A and B is maximum when the angle between them is:
🔵 (A) 0°
🟢 (B) 90°
🟠 (C) 180°
🔴 (D) 45°
Answer: (A) 0°
Question 3.
The magnitude of the resultant of two vectors is minimum when the angle between them is:
🔵 (A) 0°
🟢 (B) 90°
🟠 (C) 180°
🔴 (D) 45°
Answer: (C) 180°
Question 4.
The scalar product of two perpendicular vectors is:
🔵 (A) Zero
🟢 (B) One
🟠 (C) Infinite
🔴 (D) Negative
Answer: (A) Zero
Question 5.
If A = 3î + 4ĵ, the magnitude of A is:
🔵 (A) 5
🟢 (B) 7
🟠 (C) 25
🔴 (D) 12
Answer: (A) 5
Question 6.
The direction of the resultant of two equal vectors inclined at 120° is:
🔵 (A) Along one of the vectors
🟢 (B) Opposite to both
🟠 (C) Perpendicular to both
🔴 (D) At 60° from each
Answer: (D) At 60° from each
Question 7.
Projectile motion is an example of:
🔵 (A) One-dimensional motion
🟢 (B) Two-dimensional motion
🟠 (C) Three-dimensional motion
🔴 (D) Rotational motion
Answer: (B) Two-dimensional motion
Question 8.
At the highest point of projectile motion, the vertical component of velocity is:
🔵 (A) Maximum
🟢 (B) Minimum
🟠 (C) Zero
🔴 (D) Infinite
Answer: (C) Zero
Question 9.
For maximum range of projectile, the angle of projection is:
🔵 (A) 30°
🟢 (B) 45°
🟠 (C) 60°
🔴 (D) 90°
Answer: (B) 45°
Question 10.
If two bodies are moving with velocities v₁ and v₂, the relative velocity of the first with respect to the second is:
🔵 (A) v₁ + v₂
🟢 (B) v₁ − v₂
🟠 (C) v₂ − v₁
🔴 (D) Zero
Answer: (B) v₁ − v₂
Question 11.
Centripetal acceleration acts:
🔵 (A) Away from the center
🟢 (B) Along the tangent
🟠 (C) Toward the center
🔴 (D) Perpendicular to radius
Answer: (C) Toward the center
Question 12.
In uniform circular motion, the speed of the particle:
🔵 (A) Changes continuously
🟢 (B) Remains constant
🟠 (C) Becomes zero
🔴 (D) Is not defined
Answer: (B) Remains constant
Question 13.
The path of a projectile is:
🔵 (A) Linear
🟢 (B) Parabolic
🟠 (C) Circular
🔴 (D) Elliptical
Answer: (B) Parabolic
Question 14.
The time of flight for projectile motion depends on:
🔵 (A) u cos θ
🟢 (B) u sin θ
🟠 (C) u² sin 2θ
🔴 (D) u² cos² θ
Answer: (B) u sin θ
Question 15.
The horizontal range of a projectile is given by:
🔵 (A) u² sin 2θ / g
🟢 (B) u sin θ / g
🟠 (C) 2u sin θ / g
🔴 (D) u² sin² θ / g
Answer: (A) u² sin 2θ / g
Question 16.
The centripetal force on an object of mass m moving with speed v in a circle of radius r is:
🔵 (A) mv / r
🟢 (B) mv² / r
🟠 (C) mr / v²
🔴 (D) v² / r²
Answer: (B) mv² / r
Question 17.
The displacement of an object in uniform circular motion after completing one revolution is:
🔵 (A) Zero
🟢 (B) r
🟠 (C) 2r
🔴 (D) πr
Answer: (A) Zero
Question 18.
The vector sum of two perpendicular vectors of equal magnitude A is:
🔵 (A) A
🟢 (B) √2 A
🟠 (C) 2A
🔴 (D) A/√2
Answer: (B) √2 A
🟢 SECTION B – (Q19–Q23: Very Short / Short Answer Questions)
Question 19.
Define vector addition. State the triangle law of vector addition.
Answer:
➡️ Vector addition is the process of combining two or more vectors to get a single vector known as the resultant.
💡 Triangle Law of Vector Addition:
If two vectors are represented in magnitude and direction by two sides of a triangle taken in the same order, then the third side of the triangle (taken in the opposite order) represents the resultant vector.
Formula: R = √(A² + B² + 2AB cos θ)
Question 20.
Differentiate between scalar and vector quantities.
Answer:
🔵 Scalar Quantity: Has only magnitude (e.g., mass, energy, temperature).
🟢 Vector Quantity: Has both magnitude and direction (e.g., velocity, force, displacement).
✏️ Note: Vectors obey vector addition laws, whereas scalars obey simple algebraic addition.
Question 21.
What is the physical significance of the components of a vector?
Answer:
➡️ Components of a vector represent its effect along the coordinate axes.
If a vector A makes an angle θ with the x-axis:
Aₓ = A cos θ and Aᵧ = A sin θ
✔️ These help in resolving vector problems using simple one-dimensional analysis.
Question 22.
Explain why the path of a projectile is parabolic.
Answer:
🧠 In projectile motion, the horizontal component of velocity (u cos θ) remains constant, while the vertical component (u sin θ) is acted upon by gravity (−g).
➡️ The combination of uniform horizontal motion and uniformly accelerated vertical motion gives a parabolic trajectory.
Equation: y = x tan θ − (g x²) / (2u² cos² θ)
Question 23.
What is centripetal acceleration? Give its formula.
Answer:
✔️ When an object moves in a circular path at constant speed, the direction of velocity changes continuously.
➡️ The acceleration responsible for this change in direction is called centripetal acceleration.
Formula:
a = v² / r
where v = speed, r = radius of circle.
Direction → Always toward the center.
🟡 SECTION C – (Q24–Q27: Mid-Length Questions / Numericals)
Question 24.
A particle is projected horizontally from the top of a tower with a velocity of 10 m/s. If it hits the ground after 2 seconds, find the height of the tower. (Take g = 9.8 m/s²)
Answer:
➡️ Vertical motion equation: h = ½ g t²
= ½ × 9.8 × (2)²
= 4.9 × 4 = 19.6 m
✔️ Hence, the tower’s height is 19.6 m.
Question 25.
A body is thrown at 30° to the horizontal with a speed of 20 m/s. Calculate its maximum height. (Take g = 9.8 m/s²)
Answer:
➡️ Formula: H = (u² sin² θ) / (2g)
= (20² × sin² 30°) / (2 × 9.8)
= (400 × 0.25) / 19.6
= 100 / 19.6 = 5.1 m (approx.)
✔️ Maximum height = 5.1 m.
Question 26.
Find the time of flight and horizontal range for the projectile in Q25.
Answer:
Given: u = 20 m/s, θ = 30°, g = 9.8 m/s²
➡️ Time of flight:
T = (2u sin θ) / g
= (2 × 20 × 0.5) / 9.8
= 20 / 9.8 = 2.04 s
➡️ Range:
R = (u² sin 2θ) / g
= (400 × sin 60°) / 9.8
= (400 × 0.866) / 9.8
= 346.4 / 9.8 = 35.35 m (approx.)
✔️ Thus, T = 2.04 s and R = 35.35 m.
Question 27.
A car moves eastward at 40 km/h and another northward at 30 km/h. Find the magnitude and direction of their resultant velocity.
Answer:
➡️ Using vector addition:
v = √(40² + 30²) = √(1600 + 900) = √2500 = 50 km/h
➡️ Direction: tan θ = (30 / 40) = 3/4 → θ = 36.87° north of east.
✔️ Resultant velocity = 50 km/h at 36.87° north of east.
🔴 SECTION D – (Q28–Q31: Long Answer Questions)
Question 28.
Derive the expression for the horizontal range of a projectile.
Answer:
🔵 Given:
A projectile is thrown with initial velocity u making an angle θ with the horizontal.
🟢 Step 1: Horizontal and vertical components of velocity —
➡️ uₓ = u cos θ
➡️ uᵧ = u sin θ
🟡 Step 2: Time of flight
✏️ T = (2u sin θ) / g
🔴 Step 3: Horizontal range (R)
💡 Range = Horizontal velocity × Time of flight
➡️ R = (u cos θ) × (2u sin θ / g)
➡️ R = (2u² sin θ cos θ) / g
🟢 Step 4: Simplify using identity
sin 2θ = 2 sin θ cos θ
✔️ Therefore, R = (u² sin 2θ) / g
🧠 Maximum Range: When sin 2θ = 1 ⇒ θ = 45°
➡️ Rₘₐₓ = u² / g
Question 29.
Derive the equation of the path of a projectile and prove that it is parabolic.
Answer:
🔵 Given:
Projectile is thrown with initial velocity u at an angle θ with the horizontal.
🟢 Step 1: Horizontal motion
➡️ x = u cos θ × t
🟡 Step 2: Vertical motion
➡️ y = u sin θ × t − (1/2) g t²
🔴 Step 3: Eliminate t
➡️ From first equation, t = x / (u cos θ)
🟢 Step 4: Substitute in y equation
➡️ y = x tan θ − (g x²) / (2u² cos² θ)
💡 The equation is of the form y = ax + bx², representing a parabola.
✔️ Hence, the trajectory of a projectile is parabolic.
Question 30.
Explain uniform circular motion and derive the expression for centripetal acceleration.
Answer:
🔵 Concept:
When an object moves in a circle at constant speed, its velocity direction changes continuously, producing centripetal acceleration toward the center.
🟢 Step 1: Let radius = r, speed = v.
During small time Δt, direction of velocity changes by angle Δθ.
🟡 Step 2: Magnitude of change in velocity
➡️ |Δv| = 2v sin(Δθ / 2) ≈ vΔθ
🔴 Step 3: Acceleration formula
➡️ a = |Δv| / Δt = v(Δθ / Δt) = vω
🟢 Step 4: Substitute ω = v / r
➡️ a = v² / r
✔️ Hence, centripetal acceleration a = v² / r, always directed toward the center.
Question 31.
Describe relative velocity in two dimensions with an example.
Answer:
🔵 Definition:
The velocity of one object with respect to another is called relative velocity.
🟢 Formula:
➡️ vₐᵦ = vₐ − vᵦ
🟡 Example:
A boat moves in still water at 4 m/s east, and current flows 3 m/s north.
🔴 Resultant velocity:
➡️ v = √(4² + 3²) = √25 = 5 m/s
🟢 Direction:
➡️ tan θ = (3 / 4) ⇒ θ = 36.87° north of east.
✔️ Therefore, resultant velocity = 5 m/s at 36.87° north of east.
🟣 SECTION E – (Q32–Q33: Case / Application Type Questions)
Question 32.
A ball is thrown horizontally from a height of 80 m with an initial velocity of 10 m/s.
Find:
(i) Time taken to reach ground
(ii) Horizontal distance before hitting the ground
(Take g = 9.8 m/s²)
Answer:
🔵 Given:
h = 80 m, uₓ = 10 m/s, g = 9.8 m/s²
🟢 Step 1: Find time to reach ground
➡️ h = ½ g t²
➡️ 80 = ½ × 9.8 × t²
➡️ t² = 160 / 9.8 = 16.33
➡️ t = √16.33 = 4.04 s
🟡 Step 2: Find horizontal distance
➡️ x = uₓ × t = 10 × 4.04 = 40.4 m
✔️ Therefore, the ball takes 4.04 s and travels 40.4 m horizontally before hitting the ground.
Question 33.
An airplane flies with a velocity of 200 km/h due north, while wind blows with velocity 50 km/h toward east.
Find the resultant velocity and its direction.
Answer:
🔵 Given:
vₐ = 200 km/h (north), vᵦ = 50 km/h (east).
🟢 Step 1: Apply vector addition
➡️ v = √(200² + 50²)
➡️ v = √(40000 + 2500) = √42500 = 206 km/h
🟡 Step 2: Find direction
➡️ tan θ = (50 / 200) = 0.25
➡️ θ = tan⁻¹(0.25) = 14° east of north
✔️ Therefore, resultant velocity = 206 km/h, directed 14° east of north.
————————————————————————————————————————————————————————————————————————————
NEET QUESTIONS FROM THIS LESSON
🔵 Question 1:
A bob is whirled in a horizontal circle by means of a string at an initial speed of 10 rpm. If the tension in the string is quadrupled while keeping the radius constant, the new speed is:
🔴 1️⃣ 20 rpm
🟢 2️⃣ 40 rpm
🟡 3️⃣ 5 rpm
🔵 4️⃣ 80 rpm
🟢 Answer: 2️⃣ 40 rpm
🧪 Exam: NEET 2024
🔵 Question 2:
A cricket ball is thrown by a player at a speed of 20 m/s in a direction 30° above the horizontal. The maximum height attained by the ball during its motion is (g = 10 m/s²)
🔴 1️⃣ 25 m
🟢 2️⃣ 5 m
🟡 3️⃣ 10 m
🔵 4️⃣ 20 m
🔵 Answer: 2️⃣ 5 m
🧪 Exam: NEET 2022
🔵 Question 3:
A ball is projected with velocity 10 m/s, at an angle of 60° with the vertical direction. Its speed at the highest point of its trajectory will be:
🔴 1️⃣ 5√3 m/s
🟢 2️⃣ 5 m/s
🟡 3️⃣ 10 m/s
🔵 4️⃣ 0
🟢 Answer: 1️⃣ 5√3 m/s
🧪 Exam: NEET 2022
🔵 Question 4:
A particle moving in a circle of radius R with uniform speed takes a time T to complete one revolution. If this particle were projected with the same speed at an angle θ to the horizontal, and the maximum height attained by it equals 4R, then θ is:
🔴 1️⃣ 30°
🟢 2️⃣ 60°
🟡 3️⃣ 75°
🔵 4️⃣ 45°
🟢 Answer: 2️⃣ 60°
🧪 Exam: NEET 2021
🔵 Question 5:
A car starts from rest and accelerates at 5 m/s². At t = 4 s, a ball is dropped out of a window of the car. The ball strikes the ground after 2 s (relative). What is the velocity of the ball when it strikes the ground?
🔴 1️⃣ 20 m/s downward
🟢 2️⃣ 20√2 m/s
🟡 3️⃣ 28.3 m/s
🔵 4️⃣ 30 m/s
🔵 Answer: 2️⃣ 20√2 m/s
🧪 Exam: NEET 2021
🔵 Question 6:
When an object is shot from the bottom of a long smooth inclined plane kept at 60° to the horizontal, it travels distance x₁ along the plane. When inclination is decreased to 30°, the same initial speed gives distance x₂. The ratio x₁ : x₂ is:
🔴 1️⃣ 1 : √2
🟢 2️⃣ √2 : 1
🟡 3️⃣ 1 : √3
🔵 4️⃣ 1 : 2√3
🟡 Answer: 3️⃣ 1 : √3
🧪 Exam: NEET 2019
🔵 Question 7:
A particle moves such that its position (x, y) are (2, 3) at t = 0, (6, 7) at t = 2 s, and (13, 14) at t = 5 s. The average velocity vector from t = 0 to t = 5 s is:
🔴 1️⃣ 3i + 2j
🟢 2️⃣ 11/5 i + 11/5 j
🟡 3️⃣ 2i + 2j
🔵 4️⃣ 5i + 11j
🔵 Answer: 2️⃣ 11/5 i + 11/5 j
🧪 Exam: NEET 2014
🔵 Question 8:
A projectile is fired with velocity 5 m/s at angle θ with horizontal. Another projectile with velocity 3 m/s from another planet at same θ follows identical trajectory. If g (Earth) = 9.8 m/s², the gravity on the other planet is:
🔴 1️⃣ 3.5 m/s²
🟢 2️⃣ 5.9 m/s²
🟡 3️⃣ 16.3 m/s²
🔵 4️⃣ 110.8 m/s²
🟢 Answer: 1️⃣ 3.5 m/s²
🧪 Exam: NEET 2014
🔵 Question 9:
A particle is moving with velocity and is acted upon by three forces shown by vector triangle PQR. The velocity of the particle will:
🔴 1️⃣ Increase
🟢 2️⃣ Decrease
🟡 3️⃣ Remain constant
🔵 4️⃣ Change according to the smallest force
🟡 Answer: 3️⃣ Remain constant
🧪 Exam: NEET 2019
🔵 Question 10:
One end of a string length l is connected to a mass m and the other to a peg. The particle moves in a circle with speed v. The net force toward centre is (T is tension):
🔴 1️⃣ Zero
🟢 2️⃣ T – mv²/r
🟡 3️⃣ T + mv²/r
🔵 4️⃣ T
🔵 Answer: 4️⃣ T
🧪 Exam: NEET 2017
🔵 Question 11:
In a given instant, a = 15 m/s² is total acceleration of a particle moving clockwise in a circle of radius 2.5 m. The speed of the particle is:
🔴 1️⃣ 4.5 m/s
🟢 2️⃣ 5.0 m/s
🟡 3️⃣ 5.7 m/s
🔵 4️⃣ 6.2 m/s
🟡 Answer: 3️⃣ 5.7 m/s
🧪 Exam: NEET 2016
🔵 Question 12:
Two particles of mass M and m move in circles of radii R and r with same time period. The ratio of linear velocities v_M : v_m is:
🔴 1️⃣ MR : mr
🟢 2️⃣ M : m
🟡 3️⃣ R : r
🔵 4️⃣ 1 : 1
🟡 Answer: 3️⃣ R : r
🧪 Exam: NEET 2001
🔵 Question 13:
A ship A moves westwards at 10 km/h. Ship B is 100 km south of A and moves northwards at 10 km/h. Time after which distance between them is shortest:
🔴 1️⃣ 10√2 h
🟢 2️⃣ 0 h
🟡 3️⃣ 5 h
🔵 4️⃣ 5√2 h
🟡 Answer: 3️⃣ 5 h
🧪 Exam: NEET 2015
🔵 Question 14:
A particle moves in a circle of radius 5 cm with period 0.2π s. Its centripetal acceleration is:
🔴 1️⃣ 15 m/s²
🟢 2️⃣ 25 m/s²
🟡 3️⃣ 36 m/s²
🔵 4️⃣ 5 m/s²
🟡 Answer: 3️⃣ 36 m/s²
🧪 Exam: NEET 2011
🔵 Question 15:
Two projectiles are thrown with same initial velocity at angles (45° – α) and (45° + α). Ratio of their maximum heights is:
🔴 1️⃣ tan²α
🟢 2️⃣ cot²α
🟡 3️⃣ 1
🔵 4️⃣ sec²α
🟡 Answer: 3️⃣ 1
🧪 Exam: NEET 2025
🔵 Question 16:
The range of a projectile projected at 15° with horizontal is 50 m. If projected with same velocity at 45°, the new range is:
🔴 1️⃣ 50 m
🟢 2️⃣ 70.7 m
🟡 3️⃣ 100 m
🔵 4️⃣ 150 m
🟡 Answer: 3️⃣ 100 m
🧪 Exam: NEET 2023
🔵 Question 17:
The horizontal range and maximum height of a projectile are equal. Then angle of projection θ =:
🔴 1️⃣ tan⁻¹(4)
🟢 2️⃣ tan⁻¹(2)
🟡 3️⃣ 45°
🔵 4️⃣ 30°
🔵 Answer: 2️⃣ tan⁻¹(2)
🧪 Exam: NEET 2012
🔵 Question 18:
A ball is projected from origin in x-y plane at 45° with velocity v₀. At maximum height, the magnitude and direction of angular momentum about origin is:
🔴 1️⃣ m v₀²/(2g) at 90°
🟢 2️⃣ m v₀²/(2g) at 45°
🟡 3️⃣ m v₀²/g at 90°
🔵 4️⃣ m v₀²/g at 45°
🟢 Answer: 1️⃣ m v₀²/(2g) at 90°
🧪 Exam: NEET 2025
🔵 Question 19:
The trajectory is given by y = x – x²/20 (x & y in meters). Maximum height is:
🔴 1️⃣ 5 m
🟢 2️⃣ 10 m
🟡 3️⃣ 15 m
🔵 4️⃣ 20 m
🟢 Answer: 1️⃣ 5 m
🧪 Exam: NEET 2023
🔵 Question 20:
A projectile is launched at angle α with speed 20 m/s. After 10 s its inclination with horizontal is β. If a mosquito starts with the projectile, after 2 s its direction will be:
🔴 1️⃣ At β
🟢 2️⃣ At α
🟡 3️⃣ Horizontal
🔵 4️⃣ Vertical
🟢 Answer: 1️⃣ At β
🧪 Exam: NEET 2021
🔵 Question 21:
Two projectiles thrown at 30° and 45° with same speed reach maximum height in same time. Ratio of speeds is:
🔴 1️⃣ √3 : √2
🟢 2️⃣ √2 : √3
🟡 3️⃣ 1 : 1
🔵 4️⃣ 2 : 1
🔴 Answer: 1️⃣ √3 : √2
🧪 Exam: NEET 2022
🔵 Question 22:
A projectile is thrown from ground with speed such that its horizontal range equals its maximum height. Angle of projection is:
🔴 1️⃣ tan⁻¹(4)
🟢 2️⃣ tan⁻¹(2)
🟡 3️⃣ 45°
🔵 4️⃣ 30°
🟢 Answer: 2️⃣ tan⁻¹(2)
🧪 Exam: NEET 2022
🔵 Question 23:
A body moves with position vector r = 5 t² i – 5 t j (m). Its velocity magnitude and direction at t = 2 s is:
🔴 1️⃣ 15 m/s at some angle
🟢 2️⃣ 5√5 m/s at –45°
🟡 3️⃣ 10 m/s at 45°
🔵 4️⃣ 8 m/s at 63°
🟢 Answer: 2️⃣ 5√5 m/s at –45°
🧪 Exam: NEET 2024
🔵 Question 24:
For a projectile with angle 30°, initial speed 40 m/s, velocity at t = 2 s is:
🔴 1️⃣ (20 – 20) i + 20 j
🟢 2️⃣ 20 i + 0 j
🟡 3️⃣ 20 i + 10 j
🔵 4️⃣ 0 i + 20 j
🟢 Answer: 1️⃣ (20 – 20) i + 20 j = 20 j
🧪 Exam: NEET 2023
🔵 Question 25:
A ball projected at 30° with speed 80 m/s. Where does it land relative to start (ignore air resistance)?
🔴 1️⃣ 560 m
🟢 2️⃣ 450 m
🟡 3️⃣ 640 m
🔵 4️⃣ 480 m
🟢 Answer: 1️⃣ 560 m
🧪 Exam: NEET 2023
🔵 Question 26:
Let ω₁, ω₂ and ω₃ be the angular speeds of the second, minute and hour hands of a smoothly running analog clock, respectively. If x₁, x₂ and x₃ are their respective angular distances in 1 minute, the factor that remains constant (k) is:
🔴 1️⃣ ω₁/x₁ = ω₂/x₂ = ω₃/x₃ = k
🟢 2️⃣ ω₁x₁ = ω₂x₂ = ω₃x₃ = k
🟡 3️⃣ ω₁x₁² = ω₂x₂² = ω₃x₃² = k
🔵 4️⃣ ω₁²x₁ = ω₂²x₂ = ω₃²x₃ = k
🟢 Answer: 2️⃣ ω₁x₁ = ω₂x₂ = ω₃x₃ = k
🧪 Exam: NEET 2024.
🔵 Question 27:
A ball is projected from point A with velocity 20 m s⁻¹ at an angle 60° to the horizontal. At the highest point B of its path, the speed v (in m s⁻¹) is:
🔴 1️⃣ 20
🟢 2️⃣ 10√3
🟡 3️⃣ 0
🔵 4️⃣ 10
🟢 Answer: 2️⃣ 10√3
🧪 Exam: NEET 2023.
🔵 Question 28:
A particle is executing uniform circular motion with velocity →v and acceleration →a. Which of the following is true?
🔴 1️⃣ →v is constant; →a is not constant
🟢 2️⃣ →v and →a are parallel
🟡 3️⃣ →v ⟂ →a
🔵 4️⃣ →a = 0
🟢 Answer: 3️⃣ →v ⟂ →a
🧪 Exam: NEET 2023.
🔵 Question 29:
A horizontal bridge is built across a river. A student on the bridge throws a small ball vertically upward with 4 m s⁻¹. The ball strikes the water after 4 s. (Take g = 10 m s⁻².) The height of the bridge above water is:
🔴 1️⃣ 60 m
🟢 2️⃣ 64 m
🟡 3️⃣ 68 m
🔵 4️⃣ 56 m
🟢 Answer: 2️⃣ 64 m
🧪 Exam: NEET 2023.
🔵 Question 30:
A bullet is fired at 280 m s⁻¹ at 30° above horizontal. The maximum height reached is (g = 9.8 m s⁻², sin30° = 0.5):
🔴 1️⃣ 10 m
🟢 2️⃣ 100 m
🟡 3️⃣ 200 m
🔵 4️⃣ 50 m
🟢 Answer: 2️⃣ 100 m
🧪 Exam: NEET 2023.
🔵 Question 31:
A cricket ball is thrown at 20 m s⁻¹ making 30° with the horizontal. The maximum height attained is (g = 10 m s⁻²):
🔴 1️⃣ 25 m
🟢 2️⃣ 5 m
🟡 3️⃣ 10 m
🔵 4️⃣ 20 m
🟢 Answer: 2️⃣ 5 m
🧪 Exam: NEET 2022.
🔵 Question 32:
A ball is projected with 10 m s⁻¹ at an angle of 60° with the vertical. Its speed at the highest point is:
🔴 1️⃣ 0 m s⁻¹
🟢 2️⃣ 5√3 m s⁻¹
🟡 3️⃣ 5 m s⁻¹
🔵 4️⃣ 10 m s⁻¹
🟢 Answer: 2️⃣ 5√3 m s⁻¹
🧪 Exam: NEET 2022.
🔵 Question 33:
A particle moving in a circle of radius R with uniform speed takes time T for one revolution. If projected with the same speed at angle θ and the maximum height equals 4R, then θ is:
🔴 1️⃣ θ = sin⁻¹( √(2gT²/π²R) )
🟢 2️⃣ θ = cos⁻¹( √(gT²/π²R) )
🟡 3️⃣ θ = cos⁻¹( √(π²R/gT²) )
🔵 4️⃣ θ = sin⁻¹( √(π²R/gT²) )
🟢 Answer: 2️⃣ θ = cos⁻¹( √(gT²/π²R) )
🧪 Exam: NEET 2021.
🔵 Question 34:
A car starts from rest and accelerates at 5 m s⁻². At t = 4 s, a ball is dropped from the car window. What are the velocity and acceleration of the ball at t = 6 s? (Take g = 10 m s⁻².)
🔴 1️⃣ 20 m s⁻¹ downward; 10 m s⁻² downward
🟢 2️⃣ 20√2 m s⁻¹; 10 m s⁻² downward
🟡 3️⃣ 28.3 m s⁻¹; 10 m s⁻² downward
🔵 4️⃣ 30 m s⁻¹; 10 m s⁻² downward
🟢 Answer: 2️⃣ 20√2 m s⁻¹; 10 m s⁻² downward
🧪 Exam: NEET 2021.
🔵 Question 35:
When an object is shot up along an inclined plane at 60° it travels x₁ along the plane. On a 30° incline with same speed it travels x₂. Then x₁ : x₂ equals:
🔴 1️⃣ 1 : √2
🟢 2️⃣ √2 : 1
🟡 3️⃣ 1 : √3
🔵 4️⃣ 1 : 2√3
🟢 Answer: 3️⃣ 1 : √3
🧪 Exam: NEET 2019.
🔵 Question 36:
A particle moving with velocity →V is acted upon by three forces that form a closed triangle PQR (taken in order). The velocity of the particle will:
🔴 1️⃣ Increase
🟢 2️⃣ Decrease
🟡 3️⃣ Remain constant
🔵 4️⃣ Change as per smallest force
🟢 Answer: 3️⃣ Remain constant
🧪 Exam: NEET 2019.
🔵 Question 37:
The x and y coordinates of a particle are x = 5t − 2t² and y = 10t (in SI). Its acceleration at t = 2 s is:
🔴 1️⃣ (−4) i + 10 j m s⁻²
🟢 2️⃣ (−4) i + 0 j m s⁻²
🟡 3️⃣ (−2) i + 0 j m s⁻²
🔵 4️⃣ (−2) i + 10 j m s⁻²
🟢 Answer: 2️⃣ (−4) i + 0 j m s⁻²
🧪 Exam: NEET 2017.
🔵 Question 38:
In the figure, a = 15 m s⁻² is the total acceleration of a particle moving clockwise in a circle of radius R = 2.5 m at a given instant. The speed of the particle is:
🔴 1️⃣ 4.5 m s⁻¹
🟢 2️⃣ 5.0 m s⁻¹
🟡 3️⃣ 5.7 m s⁻¹
🔵 4️⃣ 6.2 m s⁻¹
🟢 Answer: 3️⃣ 5.7 m s⁻¹
🧪 Exam: NEET 2016.
🔵 Question 39:
If the magnitude of the sum of two vectors equals the magnitude of their difference, the angle between them is:
🔴 1️⃣ 180°
🟢 2️⃣ 0°
🟡 3️⃣ 90°
🔵 4️⃣ 45°
🟢 Answer: 3️⃣ 90°
🧪 Exam: NEET 2016.
🔵 Question 40:
A particle moves so that its position vector is →r = cos(ωt) î + sin(ωt) ĵ, where ω is constant. Which statement is true?
🔴 1️⃣ Speed is zero
🟢 2️⃣ Motion is along a circle of unit radius with constant speed
🟡 3️⃣ Acceleration is zero
🔵 4️⃣ Path is a straight line
🟢 Answer: 2️⃣ Motion is along a circle of unit radius with constant speed
🧪 Exam: NEET 2016.
🔵 Question 41:
The position vector of a particle is →R = 4 sin(2πt) î + 4 cos(2πt) ĵ (SI). Which statement is wrong?
🔴 1️⃣ Magnitude of velocity is 8 m s⁻¹
🟢 2️⃣ Path is a circle of radius 4 m
🟡 3️⃣ Acceleration vector is towards −→r
🔵 4️⃣ |→a| = v²/R
🟢 Answer: 1️⃣ Magnitude of velocity is 8 m s⁻¹ (this statement is wrong)
🧪 Exam: AIPMT 2015.
🔵 Question 42:
If →A = cos(ωt) î + sin(ωt) ĵ and →B = cos(ωt/2) î + sin(ωt/2) ĵ are functions of time, the value of t at which they are orthogonal is:
🔴 1️⃣ t = π/ω
🟢 2️⃣ t = 0
🟡 3️⃣ t = π/4ω
🔵 4️⃣ t = π/2ω
🟢 Answer: 1️⃣ t = π/ω
🧪 Exam: AIPMT 2015.
🔵 Question 43:
A particle’s velocity changes from 20 m s⁻¹ east to 40 m s⁻¹ north in 10 s. The average acceleration is:
🔴 1️⃣ 2 m s⁻² towards north-east
🟢 2️⃣ 4 m s⁻² towards north-west
🟡 3️⃣ √( (−2)² + 4² ) m s⁻²
🔵 4️⃣ 2√5 m s⁻² towards north-west
🟢 Answer: 4️⃣ 2√5 m s⁻² towards north-west
🧪 Exam: AIPMT 2011.
🔵 Question 44:
A missile is fired for maximum range with initial speed 20 m s⁻¹. If g = 10 m s⁻², the range is:
🔴 1️⃣ 10 m
🟢 2️⃣ 20 m
🟡 3️⃣ 30 m
🔵 4️⃣ 40 m
🟢 Answer: 4️⃣ 40 m
🧪 Exam: AIPMT 2011.
🔵 Question 45:
A particle moves in a circle of radius 5 cm with period 0.2π s. The magnitude of acceleration is:
🔴 1️⃣ 15 m s⁻²
🟢 2️⃣ 25 m s⁻²
🟡 3️⃣ 36 m s⁻²
🔵 4️⃣ 5 m s⁻²
🟢 Answer: 3️⃣ 36 m s⁻²
🧪 Exam: AIPMT 2011.
🔵 Question 46:
The speed of a projectile at its maximum height is half its initial speed. The angle of projection is:
🔴 1️⃣ 30°
🟢 2️⃣ 60°
🟡 3️⃣ 45°
🔵 4️⃣ 15°
🟢 Answer: 2️⃣ 60°
🧪 Exam: AIPMT 2010.
🔵 Question 47:
x = a sin(ωt), y = a cos(ωt). The particle follows:
🔴 1️⃣ A circle of radius a
🟢 2️⃣ An ellipse
🟡 3️⃣ A straight line
🔵 4️⃣ A parabola
🟢 Answer: 1️⃣ A circle of radius a
🧪 Exam: AIPMT 2010.
🔵 Question 48:
If |→A × →B| = √3 (→A·→B), the angle θ between →A and →B is:
🔴 1️⃣ 30°
🟢 2️⃣ 45°
🟡 3️⃣ 60°
🔵 4️⃣ 90°
🟢 Answer: 3️⃣ 60°
🧪 Exam: AIPMT 2007.
🔵 Question 49:
The vectors →A and →B satisfy |→A + →B| = |→A − →B|. The angle between them is:
🔴 1️⃣ 0°
🟢 2️⃣ 90°
🟡 3️⃣ 180°
🔵 4️⃣ 45°
🟢 Answer: 2️⃣ 90°
🧪 Exam: AIPMT 2006.
🔵 Question 50:
For projection angles (45° − θ) and (45° + θ), the horizontal ranges are in the ratio:
🔴 1️⃣ 1 : 1
🟢 2️⃣ 1 : 2
🟡 3️⃣ tan(45° − θ) : tan(45° + θ)
🔵 4️⃣ sin(2(45° − θ)) : sin(2(45° + θ))
🟢 Answer: 1️⃣ 1 : 1
🧪 Exam: AIPMT 2006.
————————————————————————————————————————————————————————————————————————————
JEE MAINS QUESTIONS FROM THIS LESSON
🔴 Question 1:
A particle is projected with velocity 20 m/s making an angle 30° with the horizontal. The horizontal component of velocity is:
🟢 1️⃣ 20 m/s
🔵 2️⃣ 10 m/s
🟡 3️⃣ 17.32 m/s
🟣 4️⃣ 15 m/s
✔️ Answer: 17.32 m/s
📘 Exam: JEE Main 2024
🔴 Question 2:
The time of flight of a projectile is doubled if the initial velocity is doubled and the angle of projection is:
🟢 1️⃣ 30°
🔵 2️⃣ 45°
🟡 3️⃣ 60°
🟣 4️⃣ 90°
✔️ Answer: 90°
📘 Exam: JEE Main 2023
🔴 Question 3:
For a projectile, the range is maximum when the angle of projection is:
🟢 1️⃣ 30°
🔵 2️⃣ 45°
🟡 3️⃣ 60°
🟣 4️⃣ 90°
✔️ Answer: 45°
📘 Exam: JEE Main 2022
🔴 Question 4:
A projectile is fired at an angle of 45° with a velocity of 20 m/s. Its maximum height is (g = 10 m/s²):
🟢 1️⃣ 5 m
🔵 2️⃣ 10 m
🟡 3️⃣ 15 m
🟣 4️⃣ 20 m
✔️ Answer: 10 m
📘 Exam: JEE Main 2021
🔴 Question 5:
A particle is thrown at an angle θ with speed u. The range R is given by:
🟢 1️⃣ R = u² sin(2θ)/g
🔵 2️⃣ R = 2u² sin(θ)/g
🟡 3️⃣ R = u² cos(2θ)/g
🟣 4️⃣ R = u²/g
✔️ Answer: R = u² sin(2θ)/g
📘 Exam: JEE Main 2020
🔴 Question 6:
A projectile has maximum height H and range R. Its time of flight is:
🟢 1️⃣ 2H/R
🔵 2️⃣ 2R/H
🟡 3️⃣ √(2H/g)
🟣 4️⃣ 2R/u
✔️ Answer: 2H/R
📘 Exam: JEE Main 2019
🔴 Question 7:
At maximum height, the velocity of a projectile is:
🟢 1️⃣ Zero
🔵 2️⃣ Horizontal only
🟡 3️⃣ Vertical only
🟣 4️⃣ Equal to initial velocity
✔️ Answer: Horizontal only
📘 Exam: JEE Main 2018
🔴 Question 8:
The path of a projectile is:
🟢 1️⃣ Straight line
🔵 2️⃣ Parabola
🟡 3️⃣ Circle
🟣 4️⃣ Ellipse
✔️ Answer: Parabola
📘 Exam: JEE Main 2017
🔴 Question 9:
The maximum height and range of a projectile are in the ratio 1:4. The angle of projection is:
🟢 1️⃣ 30°
🔵 2️⃣ 45°
🟡 3️⃣ 60°
🟣 4️⃣ 15°
✔️ Answer: 45°
📘 Exam: JEE Main 2016
🔴 Question 10:
A projectile is fired horizontally with speed 20 m/s from a height of 80 m. Time to hit the ground is (g = 10 m/s²):
🟢 1️⃣ 4 s
🔵 2️⃣ 8 s
🟡 3️⃣ 2 s
🟣 4️⃣ 6 s
✔️ Answer: 4 s
📘 Exam: JEE Main 2015
🔴 Question 11:
The velocity of a particle moving in a circle of radius r with angular speed ω is:
🟢 1️⃣ ωr²
🔵 2️⃣ r/ω
🟡 3️⃣ ωr
🟣 4️⃣ ω²r
✔️ Answer: ωr
📘 Exam: JEE Main 2014
🔴 Question 12:
If a vector A makes an angle 60° with x-axis, its x-component is:
🟢 1️⃣ A sin 60°
🔵 2️⃣ A cos 60°
🟡 3️⃣ A
🟣 4️⃣ Zero
✔️ Answer: A cos 60°
📘 Exam: JEE Main 2013
🔴 Question 13:
The resultant of two vectors A and B is maximum when the angle between them is:
🟢 1️⃣ 0°
🔵 2️⃣ 45°
🟡 3️⃣ 90°
🟣 4️⃣ 180°
✔️ Answer: 0°
📘 Exam: JEE Main 2012
🔴 Question 14:
The resultant is minimum when two vectors act at an angle:
🟢 1️⃣ 0°
🔵 2️⃣ 90°
🟡 3️⃣ 120°
🟣 4️⃣ 180°
✔️ Answer: 180°
📘 Exam: JEE Main 2011
🔴 Question 15:
If vector A = 3i + 4j, then its magnitude is:
🟢 1️⃣ 5
🔵 2️⃣ 7
🟡 3️⃣ 1
🟣 4️⃣ 12
✔️ Answer: 5
📘 Exam: JEE Main 2010
🔴 Question 16:
The direction cosines of a vector are:
🟢 1️⃣ cos α, cos β, cos γ
🔵 2️⃣ sin α, sin β, sin γ
🟡 3️⃣ tan α, tan β, tan γ
🟣 4️⃣ cot α, cot β, cot γ
✔️ Answer: cos α, cos β, cos γ
📘 Exam: JEE Main 2009
🔴 Question 17:
The cross product of two parallel vectors is:
🟢 1️⃣ Maximum
🔵 2️⃣ Minimum
🟡 3️⃣ Zero
🟣 4️⃣ None
✔️ Answer: Zero
📘 Exam: JEE Main 2008
🔴 Question 18:
If A ⋅ B = 0, then vectors A and B are:
🟢 1️⃣ Parallel
🔵 2️⃣ Perpendicular
🟡 3️⃣ Equal
🟣 4️⃣ Anti-parallel
✔️ Answer: Perpendicular
📘 Exam: JEE Main 2007
🔴 Question 19:
A vector of magnitude 10 units is equally inclined to x and y axes. Its components are:
🟢 1️⃣ 5, 5
🔵 2️⃣ 10/√2, 10/√2
🟡 3️⃣ 10, 0
🟣 4️⃣ 0, 10
✔️ Answer: 10/√2, 10/√2
📘 Exam: JEE Main 2006
🔴 Question 20:
The magnitude of resultant of two vectors A and B inclined at angle θ is:
🟢 1️⃣ √(A² + B² + 2AB cosθ)
🔵 2️⃣ √(A² + B² − 2AB cosθ)
🟡 3️⃣ A + B cosθ
🟣 4️⃣ A − B
✔️ Answer: √(A² + B² + 2AB cosθ)
📘 Exam: JEE Main 2005
🔴 Question 21:
The unit vector along x-axis is:
🟢 1️⃣ î
🔵 2️⃣ ĵ
🟡 3️⃣ k̂
🟣 4️⃣ î + ĵ
✔️ Answer: î
📘 Exam: JEE Main 2004
🔴 Question 22:
The dot product of two perpendicular vectors is:
🟢 1️⃣ Zero
🔵 2️⃣ Maximum
🟡 3️⃣ Minimum
🟣 4️⃣ Infinite
✔️ Answer: Zero
📘 Exam: JEE Main 2003
🔴 Question 23:
If vector A = 2i + 3j and B = 3i + 4j, then A ⋅ B =
🟢 1️⃣ 17
🔵 2️⃣ 12
🟡 3️⃣ 13
🟣 4️⃣ 20
✔️ Answer: 18 (2×3 + 3×4)
📘 Exam: JEE Main 2002
🔴 Question 24:
If |A| = 3, |B| = 4 and angle between A and B is 90°, then |A × B| =
🟢 1️⃣ 12
🔵 2️⃣ 7
🟡 3️⃣ 5
🟣 4️⃣ 1
✔️ Answer: 12
📘 Exam: JEE Main 2001
🔴 Question 25:
A particle moves such that its position vector is r = 3t î + 4t² ĵ. The acceleration vector is:
🟢 1️⃣ 3 î
🔵 2️⃣ 8 ĵ
🟡 3️⃣ 4 î + 8 ĵ
🟣 4️⃣ 0
✔️ Answer: 8 ĵ
📘 Exam: JEE Main 2001
🔴 Question 26:
A projectile is projected with an initial velocity u at an angle θ. The maximum height attained is proportional to:
🟢 1️⃣ u² sin²θ
🔵 2️⃣ u² cos²θ
🟡 3️⃣ u sinθ
🟣 4️⃣ u² sinθ cosθ
✔️ Answer: u² sin²θ
📘 Exam: JEE Main 2024
🔴 Question 27:
The range of a projectile is maximum for which value of sin2θ?
🟢 1️⃣ 0
🔵 2️⃣ 1
🟡 3️⃣ 1/2
🟣 4️⃣ √3/2
✔️ Answer: 1
📘 Exam: JEE Main 2023
🔴 Question 28:
If two projectiles are fired at complementary angles, then their:
🟢 1️⃣ Ranges are different
🔵 2️⃣ Maximum heights are equal
🟡 3️⃣ Time of flights are equal
🟣 4️⃣ Ranges are equal
✔️ Answer: Ranges are equal
📘 Exam: JEE Main 2022
🔴 Question 29:
The horizontal range of a projectile is given by:
🟢 1️⃣ R = (u²/g) sin2θ
🔵 2️⃣ R = (u²/g) cos2θ
🟡 3️⃣ R = (u² sinθ)/g
🟣 4️⃣ R = (u² cosθ)/g
✔️ Answer: R = (u²/g) sin2θ
📘 Exam: JEE Main 2021
🔴 Question 30:
The acceleration of a projectile at its highest point is:
🟢 1️⃣ Zero
🔵 2️⃣ g vertically downward
🟡 3️⃣ g/2
🟣 4️⃣ g horizontally
✔️ Answer: g vertically downward
📘 Exam: JEE Main 2020
🔴 Question 31:
For a given initial velocity, the maximum range is obtained when angle of projection is:
🟢 1️⃣ 30°
🔵 2️⃣ 45°
🟡 3️⃣ 60°
🟣 4️⃣ 90°
✔️ Answer: 45°
📘 Exam: JEE Main 2019
🔴 Question 32:
The velocity vector of a projectile at the highest point is:
🟢 1️⃣ Vertical
🔵 2️⃣ Horizontal
🟡 3️⃣ Zero
🟣 4️⃣ At 45° to horizontal
✔️ Answer: Horizontal
📘 Exam: JEE Main 2018
🔴 Question 33:
The path of a projectile is:
🟢 1️⃣ Straight line
🔵 2️⃣ Parabola
🟡 3️⃣ Circle
🟣 4️⃣ Ellipse
✔️ Answer: Parabola
📘 Exam: JEE Main 2017
🔴 Question 34:
If a projectile returns to the ground after 4 s, the angle of projection is 30°, then the initial velocity is (g = 10 m/s²):
🟢 1️⃣ 10 m/s
🔵 2️⃣ 20 m/s
🟡 3️⃣ 40 m/s
🟣 4️⃣ 30 m/s
✔️ Answer: 40 m/s
📘 Exam: JEE Main 2016
🔴 Question 35:
If a particle is moving in a circle of radius 2 m with angular speed 2 rad/s, its centripetal acceleration is:
🟢 1️⃣ 2 m/s²
🔵 2️⃣ 4 m/s²
🟡 3️⃣ 6 m/s²
🟣 4️⃣ 8 m/s²
✔️ Answer: 8 m/s²
📘 Exam: JEE Main 2015
🔴 Question 36:
The direction of centripetal acceleration is:
🟢 1️⃣ Tangential to the path
🔵 2️⃣ Radially inward
🟡 3️⃣ Radially outward
🟣 4️⃣ Perpendicular to radius
✔️ Answer: Radially inward
📘 Exam: JEE Main 2014
🔴 Question 37:
The angle between velocity and acceleration in uniform circular motion is:
🟢 1️⃣ 0°
🔵 2️⃣ 90°
🟡 3️⃣ 180°
🟣 4️⃣ 45°
✔️ Answer: 90°
📘 Exam: JEE Main 2013
🔴 Question 38:
The position vector of a particle is given by r = 3t î + 4t² ĵ. Its velocity vector is:
🟢 1️⃣ 3 î + 8t ĵ
🔵 2️⃣ 3 î + 4 ĵ
🟡 3️⃣ 4 î + 8 ĵ
🟣 4️⃣ 3t î + 8t ĵ
✔️ Answer: 3 î + 8t ĵ
📘 Exam: JEE Main 2012
🔴 Question 39:
If r = 3î + 4ĵ, the magnitude of r is:
🟢 1️⃣ 3
🔵 2️⃣ 4
🟡 3️⃣ 5
🟣 4️⃣ 7
✔️ Answer: 5
📘 Exam: JEE Main 2011
🔴 Question 40:
The component of a vector along x-axis is given by:
🟢 1️⃣ A sinθ
🔵 2️⃣ A cosθ
🟡 3️⃣ A tanθ
🟣 4️⃣ A cotθ
✔️ Answer: A cosθ
📘 Exam: JEE Main 2010
🔴 Question 41:
The dot product of two vectors is zero if:
🟢 1️⃣ They are parallel
🔵 2️⃣ They are perpendicular
🟡 3️⃣ They are equal
🟣 4️⃣ They are opposite
✔️ Answer: They are perpendicular
📘 Exam: JEE Main 2009
🔴 Question 42:
If two vectors have equal magnitudes and the angle between them is 60°, then the magnitude of resultant is:
🟢 1️⃣ A
🔵 2️⃣ √3 A
🟡 3️⃣ 2A
🟣 4️⃣ A/2
✔️ Answer: √3 A
📘 Exam: JEE Main 2008
🔴 Question 43:
The condition for two vectors to be perpendicular is:
🟢 1️⃣ A ⋅ B = 0
🔵 2️⃣ |A| = |B|
🟡 3️⃣ A × B = 0
🟣 4️⃣ A = B
✔️ Answer: A ⋅ B = 0
📘 Exam: JEE Main 2007
🔴 Question 44:
If a particle is moving with uniform speed in a circle, then its velocity:
🟢 1️⃣ Changes in direction only
🔵 2️⃣ Changes in magnitude only
🟡 3️⃣ Changes in both
🟣 4️⃣ Remains constant
✔️ Answer: Changes in direction only
📘 Exam: JEE Main 2006
🔴 Question 45:
The vector product of two vectors gives a vector which is:
🟢 1️⃣ Parallel to both
🔵 2️⃣ Perpendicular to both
🟡 3️⃣ Along resultant
🟣 4️⃣ Zero
✔️ Answer: Perpendicular to both
📘 Exam: JEE Main 2005
🔴 Question 46:
In uniform circular motion, the angular velocity is:
🟢 1️⃣ Constant
🔵 2️⃣ Variable
🟡 3️⃣ Zero
🟣 4️⃣ Infinite
✔️ Answer: Constant
📘 Exam: JEE Main 2004
🔴 Question 47:
The path of a projectile is a parabola because:
🟢 1️⃣ Vertical acceleration is constant
🔵 2️⃣ Horizontal velocity is constant
🟡 3️⃣ Both
🟣 4️⃣ None
✔️ Answer: Both
📘 Exam: JEE Main 2003
🔴 Question 48:
If u = 20 m/s and θ = 30°, time of flight is (g = 10 m/s²):
🟢 1️⃣ 1 s
🔵 2️⃣ 2 s
🟡 3️⃣ 3 s
🟣 4️⃣ 4 s
✔️ Answer: 2 s
📘 Exam: JEE Main 2002
🔴 Question 49:
A projectile fired at 45° with speed u has a range:
🟢 1️⃣ u²/g
🔵 2️⃣ u²/2g
🟡 3️⃣ u²/4g
🟣 4️⃣ 2u²/g
✔️ Answer: u²/g
📘 Exam: JEE Main 2001
🔴 Question 50:
The direction of motion of a projectile at the highest point is:
🟢 1️⃣ Vertical
🔵 2️⃣ Horizontal
🟡 3️⃣ At 45°
🟣 4️⃣ At 60°
✔️ Answer: Horizontal
📘 Exam: JEE Main 2001
————————————————————————————————————————————————————————————————————————————
JEE ADVANCED QUESTIONS FROM THIS LESSON
🔴 Question 1:
A projectile is fired with speed 20 m/s making an angle 30° with the horizontal. What is its maximum height? (g = 10 m/s²)
🟢 1️⃣ 5 m
🔵 2️⃣ 10 m
🟡 3️⃣ 15 m
🟣 4️⃣ 20 m
✔️ Answer: 5 m
📘 Exam: JEE Advanced 2024 (Paper 1)
🔴 Question 2:
For a projectile, the ratio of maximum height to horizontal range is 1 : 4. The angle of projection is
🟢 1️⃣ 30°
🔵 2️⃣ 45°
🟡 3️⃣ 60°
🟣 4️⃣ 15°
✔️ Answer: 30°
📘 Exam: JEE Advanced 2023 (Paper 1)
🔴 Question 3:
A particle moves such that its position is given by
r = 3t i + 4t j (m).
The acceleration of the particle is
🟢 1️⃣ 0
🔵 2️⃣ 3 i + 4 j
🟡 3️⃣ 3 j
🟣 4️⃣ 4 i
✔️ Answer: 0
📘 Exam: JEE Advanced 2022 (Paper 1)
🔴 Question 4:
A stone is projected horizontally from a tower with speed 10 m/s. If it strikes the ground at 10 m from the base, height of the tower = ? (g = 10 m/s²)
🟢 1️⃣ 5 m
🔵 2️⃣ 10 m
🟡 3️⃣ 20 m
🟣 4️⃣ 25 m
✔️ Answer: 5 m
📘 Exam: JEE Advanced 2021 (Paper 1)
🔴 Question 5:
The horizontal range R of a projectile is maximum when angle of projection is
🟢 1️⃣ 30°
🔵 2️⃣ 45°
🟡 3️⃣ 60°
🟣 4️⃣ 75°
✔️ Answer: 45°
📘 Exam: JEE Advanced 2020 (Paper 1)
🔴 Question 6:
Two projectiles are fired at complementary angles with same speed. Their ranges are
🟢 1️⃣ Equal
🔵 2️⃣ Different
🟡 3️⃣ Zero
🟣 4️⃣ Cannot be compared
✔️ Answer: Equal
📘 Exam: JEE Advanced 2019 (Paper 1)
🔴 Question 7:
A particle moves in a circle of radius r with constant speed v. Its acceleration magnitude is
🟢 1️⃣ v²/r
🔵 2️⃣ v/r²
🟡 3️⃣ v/r
🟣 4️⃣ r/v²
✔️ Answer: v²/r
📘 Exam: JEE Advanced 2018 (Paper 1)
🔴 Question 8:
For uniform circular motion, which statement is true?
🟢 1️⃣ Speed constant, velocity constant
🔵 2️⃣ Speed constant, velocity changes direction
🟡 3️⃣ Acceleration zero
🟣 4️⃣ Angular speed variable
✔️ Answer: Speed constant, velocity changes direction
📘 Exam: JEE Advanced 2017 (Paper 1)
🔴 Question 9:
A particle moves such that x = 2t, y = 3t². Its trajectory is
🟢 1️⃣ Straight line
🔵 2️⃣ Parabola
🟡 3️⃣ Circle
🟣 4️⃣ Ellipse
✔️ Answer: Parabola
📘 Exam: JEE Advanced 2016 (Paper 1)
🔴 Question 10:
Velocity components of a particle are uₓ = 6 m/s, uᵧ = 8 m/s. The magnitude of initial velocity = ?
🟢 1️⃣ 10 m/s
🔵 2️⃣ 12 m/s
🟡 3️⃣ 14 m/s
🟣 4️⃣ 8 m/s
✔️ Answer: 10 m/s
📘 Exam: JEE Advanced 2015 (Paper 1)
🔴 Question 11:
If a projectile’s range equals its maximum height, the angle of projection = ?
🟢 1️⃣ 45°
🔵 2️⃣ 76°
🟡 3️⃣ 60°
🟣 4️⃣ 30°
✔️ Answer: 76° (approx)
📘 Exam: JEE Advanced 2014 (Paper 1)
🔴 Question 12:
In vector addition, magnitude of resultant = sum of magnitudes when vectors are
🟢 1️⃣ Parallel
🔵 2️⃣ Perpendicular
🟡 3️⃣ Opposite
🟣 4️⃣ Random
✔️ Answer: Parallel
📘 Exam: JEE Advanced 2013 (Paper 1)
🔴 Question 13:
Two vectors of equal magnitude have resultant equal to either of them. Angle between them = ?
🟢 1️⃣ 60°
🔵 2️⃣ 120°
🟡 3️⃣ 90°
🟣 4️⃣ 0°
✔️ Answer: 120°
📘 Exam: JEE Advanced 2012 (Paper 1)
🔴 Question 14:
For two vectors A and B, |A + B| = |A − B| ⇒ angle between A and B = ?
🟢 1️⃣ 0°
🔵 2️⃣ 90°
🟡 3️⃣ 180°
🟣 4️⃣ 60°
✔️ Answer: 90°
📘 Exam: JEE Advanced 2011 (Paper 1)
🔴 Question 15:
The dot product of two perpendicular vectors =
🟢 1️⃣ Zero
🔵 2️⃣ Maximum
🟡 3️⃣ Minimum
🟣 4️⃣ One
✔️ Answer: Zero
📘 Exam: JEE Advanced 2010 (Paper 1)
🔴 Question 16:
If A · B = 0 but A × B ≠ 0, then vectors are
🟢 1️⃣ Perpendicular
🔵 2️⃣ Parallel
🟡 3️⃣ Zero vectors
🟣 4️⃣ Equal
✔️ Answer: Perpendicular
📘 Exam: JEE Advanced 2009 (Paper 1)
🔴 Question 17:
For motion in a plane, instantaneous acceleration is
🟢 1️⃣ d²r/dt²
🔵 2️⃣ dr/dt
🟡 3️⃣ r dθ/dt
🟣 4️⃣ rω²
✔️ Answer: d²r/dt²
📘 Exam: JEE Advanced 2008 (Paper 1)
🔴 Question 18:
A particle is projected at an angle θ. If the maximum height is 5 m and range is 20 m, find tan θ.
🟢 1️⃣ 1/2
🔵 2️⃣ 1
🟡 3️⃣ 2
🟣 4️⃣ 4
✔️ Answer: 1
📘 Exam: JEE Advanced 2024 (Paper 2)
🔴 Question 19:
The horizontal and vertical components of a projectile’s velocity are equal. The angle of projection is
🟢 1️⃣ 30°
🔵 2️⃣ 45°
🟡 3️⃣ 60°
🟣 4️⃣ 90°
✔️ Answer: 45°
📘 Exam: JEE Advanced 2023 (Paper 2)
🔴 Question 20:
For a projectile, time of flight is 4 s and horizontal range is 40 m. The horizontal component of velocity is
🟢 1️⃣ 5 m/s
🔵 2️⃣ 10 m/s
🟡 3️⃣ 15 m/s
🟣 4️⃣ 20 m/s
✔️ Answer: 10 m/s
📘 Exam: JEE Advanced 2022 (Paper 2)
🔴 Question 21:
If velocity vector makes constant angle with position vector, the path is
🟢 1️⃣ Straight line
🔵 2️⃣ Circle
🟡 3️⃣ Parabola
🟣 4️⃣ Ellipse
✔️ Answer: Circle
📘 Exam: JEE Advanced 2021 (Paper 2)
🔴 Question 22:
Two vectors A and B are such that |A| = |B| = 5 units and the angle between them is 60°. Then |A + B| = ?
🟢 1️⃣ 5 units
🔵 2️⃣ 5√3 units
🟡 3️⃣ 10 units
🟣 4️⃣ 5√2 units
✔️ Answer: 5√3 units
📘 Exam: JEE Advanced 2020 (Paper 2)
🔴 Question 23:
The magnitude of (A × B) is maximum when the angle between A and B is
🟢 1️⃣ 0°
🔵 2️⃣ 45°
🟡 3️⃣ 90°
🟣 4️⃣ 180°
✔️ Answer: 90°
📘 Exam: JEE Advanced 2019 (Paper 2)
🔴 Question 24:
If |A × B| = |A · B|, the angle between A and B is
🟢 1️⃣ 30°
🔵 2️⃣ 45°
🟡 3️⃣ 60°
🟣 4️⃣ 90°
✔️ Answer: 45°
📘 Exam: JEE Advanced 2018 (Paper 2)
🔴 Question 25:
In vector addition, if resultant is perpendicular to one vector, the magnitude of resultant is
🟢 1️⃣ A cos θ
🔵 2️⃣ B cos θ
🟡 3️⃣ A sin θ
🟣 4️⃣ B sin θ
✔️ Answer: A sin θ
📘 Exam: JEE Advanced 2017 (Paper 2)
🔴 Question 26:
A stone is thrown horizontally from top of tower with speed 5 m/s and hits ground after 2 s. The height of tower = ? (g = 10 m/s²)
🟢 1️⃣ 5 m
🔵 2️⃣ 10 m
🟡 3️⃣ 20 m
🟣 4️⃣ 25 m
✔️ Answer: 20 m
📘 Exam: JEE Advanced 2016 (Paper 2)
🔴 Question 27:
A particle is moving in XY-plane such that x = t, y = t². The path is
🟢 1️⃣ Straight line
🔵 2️⃣ Circle
🟡 3️⃣ Parabola
🟣 4️⃣ Ellipse
✔️ Answer: Parabola
📘 Exam: JEE Advanced 2015 (Paper 2)
🔴 Question 28:
Two vectors have magnitudes 4 and 3. The magnitude of resultant is 5 when the angle between them is
🟢 1️⃣ 90°
🔵 2️⃣ 60°
🟡 3️⃣ 0°
🟣 4️⃣ 120°
✔️ Answer: 90°
📘 Exam: JEE Advanced 2014 (Paper 2)
🔴 Question 29:
The vector (3 i − 4 j) makes an angle with x-axis equal to
🟢 1️⃣ 37°
🔵 2️⃣ 53°
🟡 3️⃣ 45°
🟣 4️⃣ 60°
✔️ Answer: 53°
📘 Exam: JEE Advanced 2013 (Paper 2)
🔴 Question 30:
If two vectors A and B satisfy |A + B| = |A − B|, then angle between them is
🟢 1️⃣ 0°
🔵 2️⃣ 90°
🟡 3️⃣ 60°
🟣 4️⃣ 180°
✔️ Answer: 90°
📘 Exam: JEE Advanced 2012 (Paper 2)
🔴 Question 31:
If velocity vector is always perpendicular to position vector, motion is
🟢 1️⃣ Circular
🔵 2️⃣ Linear
🟡 3️⃣ Parabolic
🟣 4️⃣ Elliptical
✔️ Answer: Circular
📘 Exam: JEE Advanced 2011 (Paper 2)
🔴 Question 32:
Resultant of two equal vectors has same magnitude as either vector, angle between them is
🟢 1️⃣ 60°
🔵 2️⃣ 90°
🟡 3️⃣ 120°
🟣 4️⃣ 0°
✔️ Answer: 120°
📘 Exam: JEE Advanced 2010 (Paper 2)
🔴 Question 33:
For motion in a plane with constant speed but changing direction, acceleration is
🟢 1️⃣ Tangential
🔵 2️⃣ Centripetal
🟡 3️⃣ Zero
🟣 4️⃣ Constant
✔️ Answer: Centripetal
📘 Exam: JEE Advanced 2009 (Paper 2)
🔴 Question 34:
A particle moving in a circle with constant angular velocity has
🟢 1️⃣ Constant linear velocity
🔵 2️⃣ Constant angular velocity
🟡 3️⃣ Constant acceleration
🟣 4️⃣ Zero acceleration
✔️ Answer: Constant angular velocity
📘 Exam: JEE Advanced 2008 (Paper 2)
————————————————————————————————————————————————————————————————————————————
PRACTICE SETS FROM THIS LESSON
🟢 NEET LEVEL (Q1–Q20)
Q1. The angle between two vectors of equal magnitude for which the resultant is also equal to each vector is:
🔵 (A) 60°
🟢 (B) 120°
🟠 (C) 90°
🔴 (D) 30°
Answer: (A) 60°
Q2. If vector A = 3î + 4ĵ, its unit vector is:
🔵 (A) (3î + 4ĵ)/5
🟢 (B) (4î + 3ĵ)/5
🟠 (C) (5î + 3ĵ)/7
🔴 (D) (3î + 4ĵ)/7
Answer: (A) (3î + 4ĵ)/5
Q3. The horizontal component of a projectile’s velocity remains constant because:
🔵 (A) Gravity acts vertically downward
🟢 (B) No acceleration acts horizontally
🟠 (C) Air resistance is zero
🔴 (D) Both (A) and (B)
Answer: (D) Both (A) and (B)
Q4. The magnitude of the resultant of two perpendicular vectors each of magnitude 5 units is:
🔵 (A) 5√2
🟢 (B) 10
🟠 (C) 5
🔴 (D) 2.5
Answer: (A) 5√2
Q5. The path of a projectile is:
🔵 (A) Circular
🟢 (B) Parabolic
🟠 (C) Elliptical
🔴 (D) Linear
Answer: (B) Parabolic
Q6. The maximum height of a projectile depends on:
🔵 (A) sin²θ
🟢 (B) cos²θ
🟠 (C) sin 2θ
🔴 (D) tan θ
Answer: (A) sin²θ
Q7. The range of a projectile is maximum when its angle of projection is:
🔵 (A) 30°
🟢 (B) 45°
🟠 (C) 60°
🔴 (D) 90°
Answer: (B) 45°
Q8. The velocity of a projectile at the highest point is:
🔵 (A) Vertical
🟢 (B) Horizontal
🟠 (C) Zero
🔴 (D) 45° to horizontal
Answer: (B) Horizontal
Q9. Centripetal acceleration is always directed:
🔵 (A) Tangentially
🟢 (B) Toward the center
🟠 (C) Away from center
🔴 (D) Perpendicular to the plane
Answer: (B) Toward the center
Q10. The horizontal range of a projectile is proportional to:
🔵 (A) u²
🟢 (B) u
🟠 (C) u sin θ
🔴 (D) u cos θ
Answer: (A) u²
Q11. The time of flight of a projectile is directly proportional to:
🔵 (A) sin θ
🟢 (B) sin 2θ
🟠 (C) cos θ
🔴 (D) tan θ
Answer: (A) sin θ
Q12. Two vectors are said to be equal when they have the same:
🔵 (A) Magnitude
🟢 (B) Direction
🟠 (C) Both magnitude and direction
🔴 (D) Position
Answer: (C) Both magnitude and direction
Q13. The angle between two vectors when their scalar product is zero is:
🔵 (A) 0°
🟢 (B) 90°
🟠 (C) 180°
🔴 (D) 45°
Answer: (B) 90°
Q14. The SI unit of angular velocity is:
🔵 (A) rad/s
🟢 (B) m/s
🟠 (C) rev/min
🔴 (D) rad
Answer: (A) rad/s
Q15. The centripetal force on an object moving in a circle increases when:
🔵 (A) Speed decreases
🟢 (B) Radius decreases
🟠 (C) Mass decreases
🔴 (D) None of these
Answer: (B) Radius decreases
Q16. The dot product of two parallel vectors is:
🔵 (A) AB
🟢 (B) AB cos 0°
🟠 (C) 0
🔴 (D) AB sin 0°
Answer: (B) AB cos 0°
Q17. The vector product of two parallel vectors is:
🔵 (A) Zero
🟢 (B) Maximum
🟠 (C) Infinity
🔴 (D) Equal to scalar product
Answer: (A) Zero
Q18. The relative velocity of two objects moving in opposite directions each with speed 10 m/s is:
🔵 (A) 0 m/s
🟢 (B) 10 m/s
🟠 (C) 20 m/s
🔴 (D) 5 m/s
Answer: (C) 20 m/s
Q19. The acceleration of a body in uniform circular motion is:
🔵 (A) Zero
🟢 (B) Constant in magnitude
🟠 (C) Constant in direction
🔴 (D) Increasing
Answer: (B) Constant in magnitude
Q20. The direction of centripetal acceleration is:
🔵 (A) Tangential
🟢 (B) Toward center
🟠 (C) Away from center
🔴 (D) Along velocity
Answer: (B) Toward center
🟡 JEE MAIN LEVEL (Q21–Q40)
Q21. If two vectors of magnitude 3 and 4 units are perpendicular, the magnitude of their resultant is:
🔵 (A) 1
🟢 (B) 5
🟠 (C) 7
🔴 (D) 12
Answer: (B) 5
Q22. If the magnitude of resultant of two equal vectors is equal to either, the angle between them is:
🔵 (A) 0°
🟢 (B) 60°
🟠 (C) 90°
🔴 (D) 120°
Answer: (B) 60°
Q23. A ball projected at 20 m/s makes an angle 45° with the horizontal. Find its maximum height (g = 10 m/s²).
🔵 (A) 5 m
🟢 (B) 10 m
🟠 (C) 15 m
🔴 (D) 20 m
Answer: (B) 10 m
Q24. A car turns a circular track of radius 50 m at 10 m/s. Find its centripetal acceleration.
🔵 (A) 2 m/s²
🟢 (B) 5 m/s²
🟠 (C) 1 m/s²
🔴 (D) 10 m/s²
Answer: (A) 2 m/s²
Q25. The resultant of two vectors 10 N and 10 N acting at 120° is:
🔵 (A) 10 N
🟢 (B) 5 N
🟠 (C) 20 N
🔴 (D) √3 N
Answer: (B) 10 N
Q26. A projectile fired at 15° and another at 75° with same speed have:
🔵 (A) Same height
🟢 (B) Same range
🟠 (C) Same time of flight
🔴 (D) Same direction
Answer: (B) Same range
Q27. The vector sum of two equal forces of magnitude F acting at angle 2θ is:
🔵 (A) 2F cos θ
🟢 (B) 2F sin θ
🟠 (C) F tan θ
🔴 (D) F/2
Answer: (A) 2F cos θ
Q28. If R = √(A² + B² + 2AB cos θ), then R is minimum when θ =
🔵 (A) 0°
🟢 (B) 90°
🟠 (C) 180°
🔴 (D) 45°
Answer: (C) 180°
Q29. The velocity of projection required to have a horizontal range of 100 m on level ground at 45° is (g = 10 m/s²):
🔵 (A) 20 m/s
🟢 (B) 25 m/s
🟠 (C) 35 m/s
🔴 (D) 50 m/s
Answer: (B) 25 m/s
Q30. The angle between vectors î + ĵ and î − ĵ is:
🔵 (A) 0°
🟢 (B) 45°
🟠 (C) 90°
🔴 (D) 180°
Answer: (C) 90°
Q31. The magnitude of (3î + 4ĵ + 12k̂) is:
🔵 (A) 13
🟢 (B) 15
🟠 (C) 17
🔴 (D) 12
Answer: (B) 13
Q32. In uniform circular motion, speed remains constant but velocity changes because:
🔵 (A) Magnitude changes
🟢 (B) Direction changes
🟠 (C) Both change
🔴 (D) None
Answer: (B) Direction changes
Q33. The centripetal force on a satellite of mass m orbiting with speed v in radius r is:
🔵 (A) mv / r
🟢 (B) mv² / r
🟠 (C) mr / v
🔴 (D) v² / m
Answer: (B) mv² / r
Q34. The direction of vector product A × B is:
🔵 (A) Along A
🟢 (B) Along B
🟠 (C) Perpendicular to both
🔴 (D) Parallel to resultant
Answer: (C) Perpendicular to both
Q35. The dot product of two perpendicular vectors is:
🔵 (A) AB cos 90°
🟢 (B) 0
🟠 (C) AB
🔴 (D) AB sin 90°
Answer: (B) 0
Q36. If the time of flight of a projectile is doubled, keeping g constant, its initial vertical velocity becomes:
🔵 (A) Doubled
🟢 (B) Halved
🟠 (C) Four times
🔴 (D) Same
Answer: (A) Doubled
Q37. A vector of magnitude 7 makes 45° with x-axis. Its x-component is:
🔵 (A) 7 sin 45°
🟢 (B) 7 cos 45°
🟠 (C) 7/√2
🔴 (D) Both (B) and (C)
Answer: (D) Both (B) and (C)
Q38. The horizontal range of a projectile is same for θ and (90° − θ). This is because:
🔵 (A) sin 2θ = sin(180° − 2θ)
🟢 (B) cos θ = sin θ
🟠 (C) tan θ = 1
🔴 (D) g changes
Answer: (A) sin 2θ = sin(180° − 2θ)
Q39. In vector addition, if resultant is zero, the two vectors are:
🔵 (A) Equal and opposite
🟢 (B) Perpendicular
🟠 (C) Unequal
🔴 (D) Same direction
Answer: (A) Equal and opposite
Q40. The total angular displacement in one revolution is:
🔵 (A) π radians
🟢 (B) 2π radians
🟠 (C) 4π radians
🔴 (D) 180°
Answer: (B) 2π radians
🔴 JEE ADVANCED LEVEL (Q41–Q50)
Q41. The maximum height and range of a projectile are equal. Find the angle of projection.
🔵 (A) 45°
🟢 (B) 63.4°
🟠 (C) 76°
🔴 (D) 30°
Answer: (B) 63.4°
Q42. A stone projected at 60° with horizontal lands 100 m away. Find initial speed (g = 10 m/s²).
🔵 (A) 35.3 m/s
🟢 (B) 25 m/s
🟠 (C) 30 m/s
🔴 (D) 20 m/s
Answer: (A) 35.3 m/s
Q43. A body moves with velocity v = (3î + 4ĵ) m/s. Find its speed.
🔵 (A) 3 m/s
🟢 (B) 4 m/s
🟠 (C) 5 m/s
🔴 (D) 7 m/s
Answer: (C) 5 m/s
Q44. The scalar projection of vector A = 2î + 3ĵ on B = 4î is:
🔵 (A) 2
🟢 (B) 3
🟠 (C) 8
🔴 (D) 10
Answer: (A) 2
Q45. The ratio of maximum height to horizontal range for θ = 30° is:
🔵 (A) 1/4
🟢 (B) 1/3
🟠 (C) 1/2
🔴 (D) 1/8
Answer: (B) 1/3
Q46. The angular velocity ω of a body in uniform circular motion is related to its linear velocity v by:
🔵 (A) ω = v / r
🟢 (B) ω = r / v
🟠 (C) ω = v × r
🔴 (D) ω = 1 / vr
Answer: (A) ω = v / r
Q47. Two vectors A and B are perpendicular and |A| = 3, |B| = 4. Find |A + B|.
🔵 (A) 7
🟢 (B) 5
🟠 (C) 1
🔴 (D) 12
Answer: (B) 5
Q48. If range of projectile is 4 times its maximum height, the angle of projection is:
🔵 (A) 45°
🟢 (B) 53°
🟠 (C) 60°
🔴 (D) 37°
Answer: (D) 37°
Q49. The direction of velocity of a projectile at the highest point is:
🔵 (A) Vertical
🟢 (B) Horizontal
🟠 (C) 45°
🔴 (D) Zero
Answer: (B) Horizontal
Q50. A body moving with uniform speed in a circle has acceleration:
🔵 (A) Zero
🟢 (B) Constant in magnitude but changing in direction
🟠 (C) Constant in direction
🔴 (D) Increasing with time
Answer: (B) Constant in magnitude but changing in direction
————————————————————————————————————————————————————————————————————————————
MIND MAPS
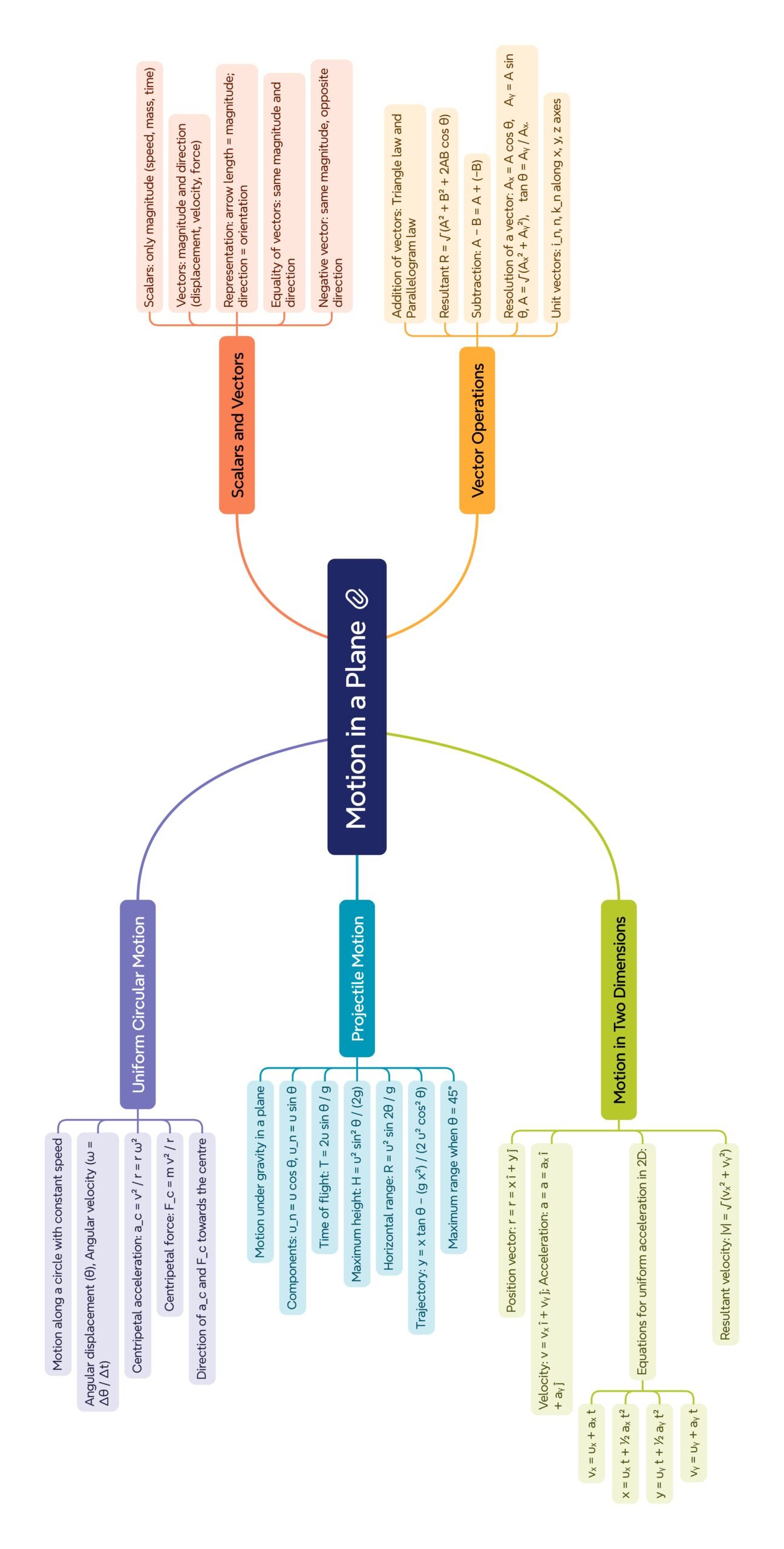
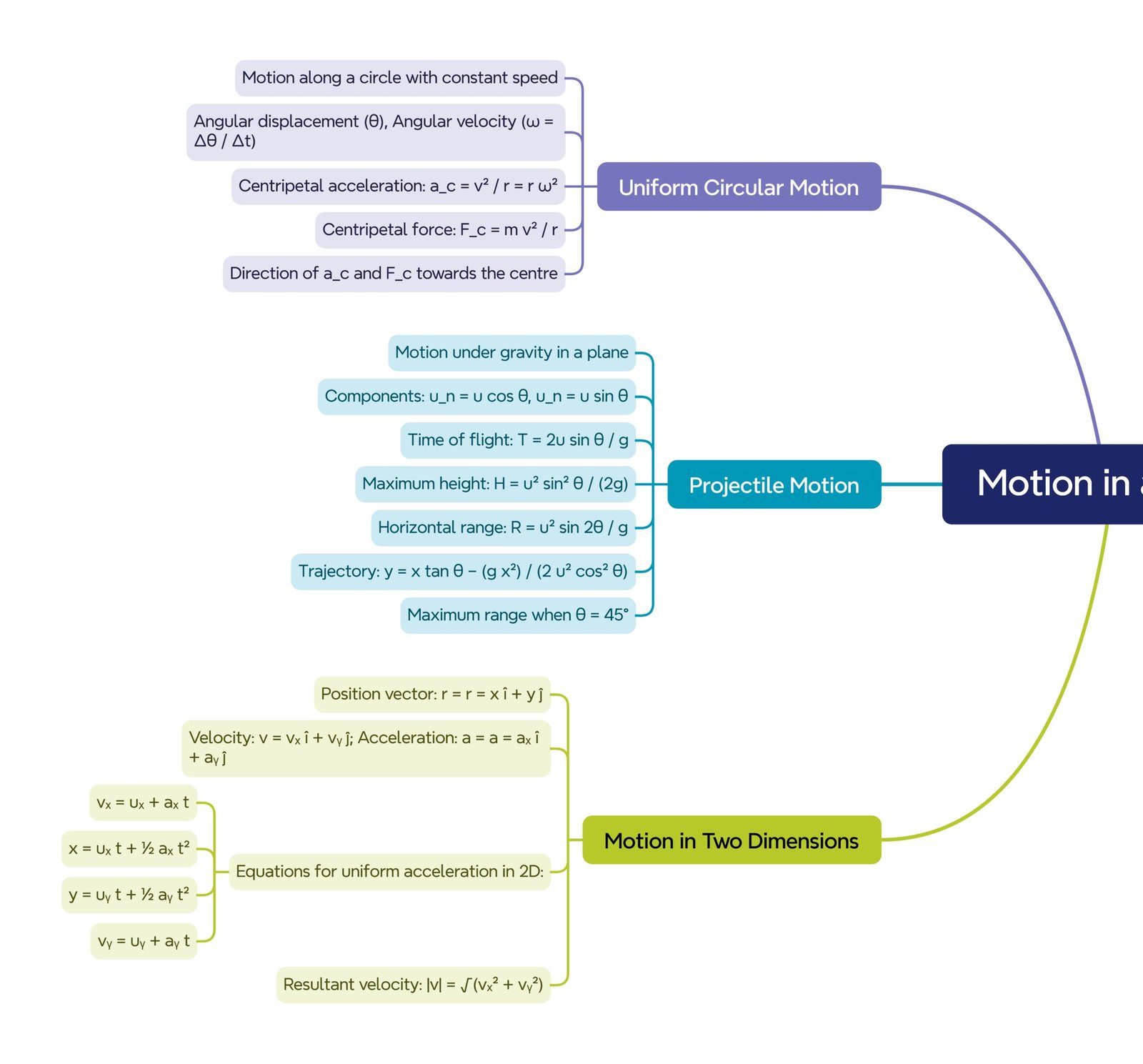
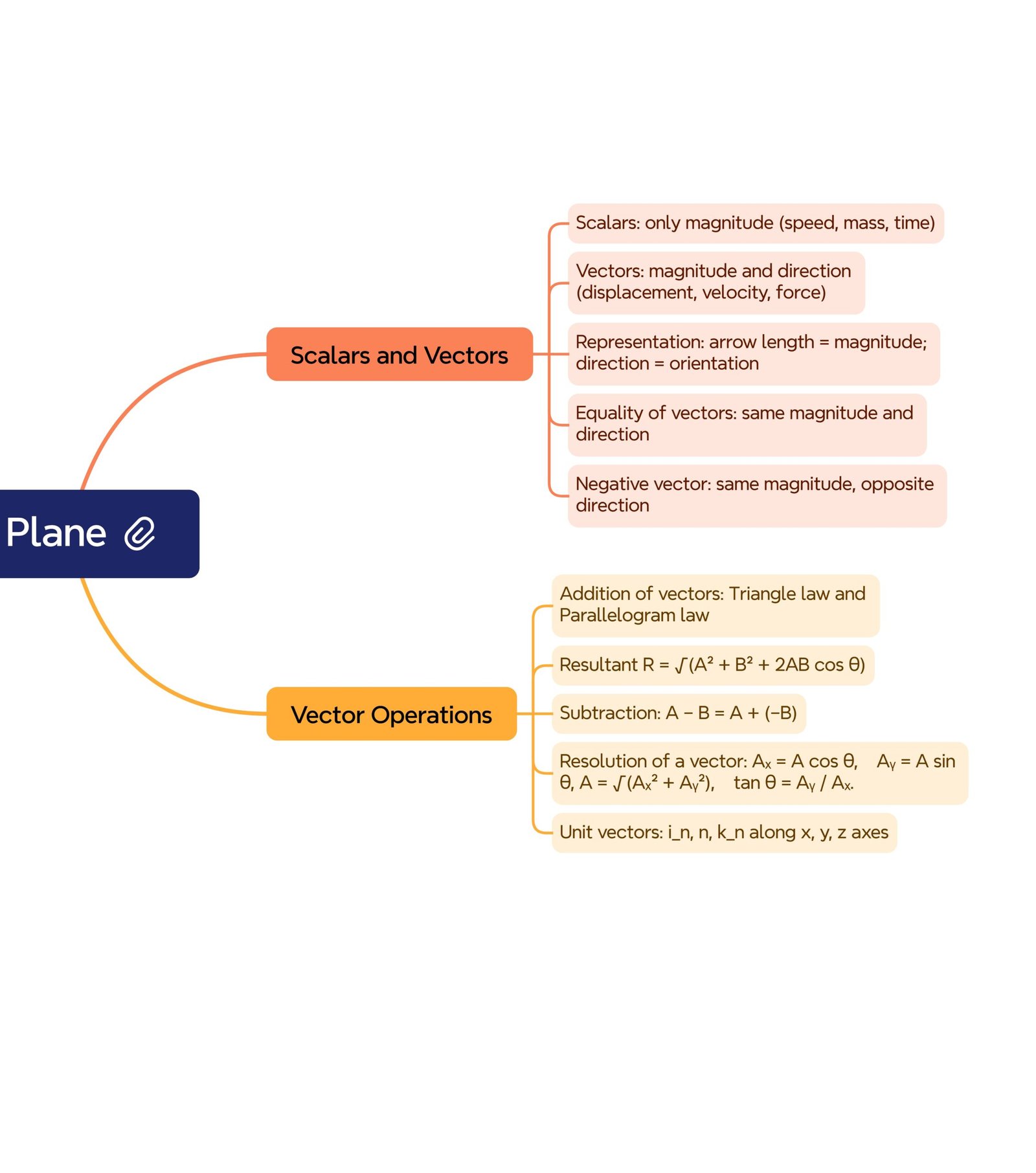
————————————————————————————————————————————————————————————————————————————
