Class 11 : Maths (In English) – Lesson 7. Binomial Theorem
EXPLANATION & SUMMARY
🔷 Explanation (~1700 words)
🔵 Introduction
The Binomial Theorem gives a formula to expand expressions of the form (a + b)ⁿ, where n is a positive integer.
It allows direct calculation of each term without multiplying repeatedly.
💡 Concept:
“Binomial” means two terms — examples: (x + y), (a − b), (2p + 3q).
🟢 1. Statement of the Theorem
For any positive integer n,
➡ (a + b)ⁿ = Σ (r = 0 → n) [ nCᵣ · aⁿ⁻ʳ · bʳ ]
Or explicitly:
(a + b)ⁿ = nC₀·aⁿ + nC₁·aⁿ⁻¹·b + nC₂·aⁿ⁻²·b² + … + nCₙ·bⁿ
🟡 2. Factorial and Binomial Coefficient
🔹 Factorial (n!)
n! = n × (n − 1) × (n − 2) × … × 3 × 2 × 1
By definition: 0! = 1
🔹 Binomial Coefficient
nCᵣ = n! / [r! × (n − r)!]
It represents the coefficient of the term containing aⁿ⁻ʳ·bʳ.
✏️ Note:
nC₀ = nCₙ = 1
nC₁ = n
nC₂ = n(n − 1)/2
🔴 3. General Term
The (r + 1)ᵗʰ term in the expansion of (a + b)ⁿ is:
➡ Tᵣ₊₁ = nCᵣ · aⁿ⁻ʳ · bʳ
💡 Example:
In (x + 2)⁵,
T₃ = ⁵C₂·x³·2² = 10·x³·4 = 40x³
🔵 4. Total Number of Terms
In (a + b)ⁿ,
➡ Number of terms = n + 1
Example: (x + y)³ has 4 terms.
🟢 5. Coefficient of a Particular Term
Coefficient of aᵐ·bᵏ is obtained from term where exponents match.
Coefficient = nCᵏ
💡 Example:
Expand (x + y)⁴.
Term with x²·y² = ⁴C₂·x²·y² → coefficient = 6.
🟡 6. Middle Term(s)
If n is even → 2 middle terms: T₍n/2₊1₎ and T₍n/2₊2₎
If n is odd → 1 middle term: T₍(n+1)/2₎
💡 Example:
For (a + b)⁴ → n = 4 → middle: T₃, T₄
For (a + b)⁵ → n = 5 → middle: T₃
🔴 7. Properties of Binomial Coefficients
🔹 1) nC₀ = nCₙ = 1
🔹 2) nCᵣ = nC₍n₋ᵣ₎
🔹 3) nCᵣ₊₁ / nCᵣ = (n − r)/(r + 1)
🔹 4) Σ (r = 0 → n) nCᵣ = 2ⁿ
🔹 5) Σ nCᵣ² = 2nCn
✔ These help in simplifications.
🟢 8. Expansion of (a − b)ⁿ
Replace b with (−b):
➡ (a − b)ⁿ = nC₀·aⁿ − nC₁·aⁿ⁻¹·b + nC₂·aⁿ⁻²·b² − … + (−1)ⁿ·nCₙ·bⁿ
🌀 Signs alternate.
🟡 9. Special Expansions
✔ (1 + x)ⁿ = 1 + nC₁x + nC₂x² + … + nCₙxⁿ
✔ (1 − x)ⁿ = 1 − nC₁x + nC₂x² − nC₃x³ + … + (−1)ⁿnCₙxⁿ
Useful for approximations.
🔵 10. Finding a Specific Term
Example 1: Find 5th term in (2x + 3)⁷
T₅ = ⁷C₄·(2x)³·3⁴ = 35·8x³·81 = 22680x³
Example 2: Term independent of x in (x² + 1/x)⁶
Tᵣ₊₁ = ⁶Cᵣ·(x²)⁶⁻ʳ·(1/x)ʳ = ⁶Cᵣ·x^(12−3r)
For independence: 12 − 3r = 0 → r = 4
Term = ⁶C₄ = 15
🟢 11. Approximation for Small x
For |x| < 1 and small,
➡ (1 + x)ⁿ ≈ 1 + n·x + [n(n−1)/2]·x² + …
💡 Example:
Find (1.02)⁵ ≈ 1 + 5(0.02) + 10(0.02)² = 1 + 0.1 + 0.004 = 1.104
🟡 12. Pascal’s Triangle
It shows binomial coefficients for each power.
Row 0: 1
Row 1: 1 1
Row 2: 1 2 1
Row 3: 1 3 3 1
Row 4: 1 4 6 4 1
Row 5: 1 5 10 10 5 1
🔹 Each number = sum of two above.
nCᵣ = (n−1)C₍r−1₎ + (n−1)Cᵣ
🔴 13. Identities
1️⃣ (1 + x)ⁿ(1 + x)ᵐ = (1 + x)ⁿ⁺ᵐ
2️⃣ (1 + x)ⁿ(1 − x)ⁿ = (1 − x²)ⁿ
3️⃣ (a + b)ⁿ + (a − b)ⁿ = 2[terms with even powers of b]
4️⃣ (a + b)ⁿ − (a − b)ⁿ = 2[terms with odd powers of b]
🟢 14. Examples
Example 1: Expand (x + 1)³
(x + 1)³ = ³C₀x³ + ³C₁x² + ³C₂x + ³C₃
= 1·x³ + 3·x² + 3·x + 1
➡ x³ + 3x² + 3x + 1
Example 2: Coefficient of x⁴ in (1 + x)⁸
Term: ⁸C₄x⁴ → Coefficient = 70
Example 3: No. of terms in (2a − 3b)⁵ = 5 + 1 = 6
🟡 15. Binomial Series (for non-integer n)
For real n (not necessarily integer):
➡ (1 + x)ⁿ = 1 + n·x + [n(n−1)/2!]·x² + [n(n−1)(n−2)/3!]·x³ + …
Valid for |x| < 1.
Used in Calculus.
🔵 16. Key Points Summary
✔ Formula: (a + b)ⁿ = Σ nCᵣ·aⁿ⁻ʳ·bʳ
✔ Total terms = n + 1
✔ General term = nCᵣ·aⁿ⁻ʳ·bʳ
✔ Alternate signs if (a − b)ⁿ
✔ Sum of coefficients = 2ⁿ
✔ Middle term logic (even/odd)
✔ Approximation for small x
🔷 Summary (~300 words)
🔹 Definition:
Binomial Theorem expands (a + b)ⁿ into n + 1 terms.
🔹 Formula:
(a + b)ⁿ = nC₀aⁿ + nC₁aⁿ⁻¹b + nC₂aⁿ⁻²b² + … + nCₙbⁿ
🔹 nCr Formula:
nCr = n! / [r!·(n−r)!]
Properties:
• nC₀ = nCₙ = 1
• nCr = nC(n−r)
• Sum of coefficients = 2ⁿ
🔹 General Term:
Tᵣ₊₁ = nCᵣ·aⁿ⁻ʳ·bʳ
🔹 Middle Term:
If n even → two middle terms
If n odd → one middle term
🔹 For (a − b)ⁿ:
Signs alternate
Sum of coefficients = 0
🔹 Applications:
• Finding coefficients
• Approximation
• Identity proofs
• Independent term
🔹 Pascal’s Triangle:
Shows coefficients row-wise.
Each coefficient = sum of two above it.
🔹 Binomial Series:
(1 + x)ⁿ = 1 + nx + n(n−1)/2! x² + …
(valid if |x| < 1)
📝 Quick Recap
🔹 (a + b)ⁿ = Σ nCᵣ·aⁿ⁻ʳ·bʳ
🔹 Total terms = n + 1
🔹 General term: Tᵣ₊₁ = nCᵣ·aⁿ⁻ʳ·bʳ
🔹 For (a − b)ⁿ → alternate signs
🔹 Sum of coefficients = 2ⁿ
🔹 Middle term logic (even/odd)
🔹 Use for coefficients, approximation, independent term
————————————————————————————————————————————————————————————————————————————
QUESTIONS FROM TEXTBOOK
🧠 Exercise 7.1
🔵 Question 1:
Expand (1 − 2x)⁵
🟢 Answer:
Using Binomial Theorem:
(a + b)ⁿ = Σ₍ᵣ₌₀₎ⁿ ⁿCᵣ aⁿ⁻ʳ bʳ
Here, a = 1, b = −2x, n = 5
➡️ (1 − 2x)⁵ = Σ₍ᵣ₌₀₎⁵ ⁵Cᵣ (1)⁵⁻ʳ (−2x)ʳ
= ⁵C₀ − 2⁵C₁x + 4⁵C₂x² − 8⁵C₃x³ + 16⁵C₄x⁴ − 32⁵C₅x⁵
Compute coefficients:
⁵C₀=1, ⁵C₁=5, ⁵C₂=10, ⁵C₃=10, ⁵C₄=5, ⁵C₅=1
➡️ (1 − 2x)⁵ = 1 − 10x + 40x² − 80x³ + 80x⁴ − 32x⁵
✔️ Final Answer: 1 − 10x + 40x² − 80x³ + 80x⁴ − 32x⁵
🔵 Question 2:
Expand ( (2/x) − (x/2) )⁵
🟢 Answer:
Let a = (2/x), b = −(x/2), n = 5
Using Binomial Theorem:
(a + b)ⁿ = Σ₍ᵣ₌₀₎ⁿ ⁿCᵣ aⁿ⁻ʳ bʳ
➡️ ((2/x) − (x/2))⁵ = Σ₍ᵣ₌₀₎⁵ ⁵Cᵣ (2/x)⁵⁻ʳ (−x/2)ʳ
= Σ₍ᵣ₌₀₎⁵ ⁵Cᵣ (−1)ʳ 2⁵⁻ʳ x⁻⁽⁵⁻ʳ⁾ × xʳ / 2ʳ
Simplify each term:
Coefficient = ⁵Cᵣ × (−1)ʳ × 2⁵⁻ʳ / 2ʳ = ⁵Cᵣ × (−1)ʳ × 2⁵⁻²ʳ
Power of x = (r − (5 − r)) = 2r − 5
So term = ⁵Cᵣ (−1)ʳ 2⁵⁻²ʳ x²ʳ⁻⁵
✔️ Final Answer: Σ₍ᵣ₌₀₎⁵ ⁵Cᵣ (−1)ʳ 2⁵⁻²ʳ x²ʳ⁻⁵
🔵 Question 3:
Expand (2x − 3)⁶
🟢 Answer:
a = 2x, b = −3, n = 6
➡️ (2x − 3)⁶ = Σ₍ᵣ₌₀₎⁶ ⁶Cᵣ (2x)⁶⁻ʳ (−3)ʳ
= Σ₍ᵣ₌₀₎⁶ ⁶Cᵣ (−1)ʳ 2⁶⁻ʳ × 3ʳ × x⁶⁻ʳ
✔️ Final Answer: Σ₍ᵣ₌₀₎⁶ ⁶Cᵣ (−1)ʳ 2⁶⁻ʳ 3ʳ x⁶⁻ʳ
🔵 Question 4:
Expand ( (x/3) + (1/x) )⁵
🟢 Answer:
a = x/3, b = 1/x, n = 5
➡️ (x/3 + 1/x)⁵ = Σ₍ᵣ₌₀₎⁵ ⁵Cᵣ (x/3)⁵⁻ʳ (1/x)ʳ
= Σ₍ᵣ₌₀₎⁵ ⁵Cᵣ × x⁵⁻ʳ / 3⁵⁻ʳ × x⁻ʳ
= Σ₍ᵣ₌₀₎⁵ ⁵Cᵣ × 3⁻⁽⁵⁻ʳ⁾ × x⁵⁻²ʳ
✔️ Final Answer: Σ₍ᵣ₌₀₎⁵ ⁵Cᵣ 3ʳ⁻⁵ x⁵⁻²ʳ
🔵 Question 5:
Expand (x + 1/x)⁶
🟢 Answer:
a = x, b = 1/x, n = 6
➡️ (x + 1/x)⁶ = Σ₍ᵣ₌₀₎⁶ ⁶Cᵣ x⁶⁻ʳ × x⁻ʳ
= Σ₍ᵣ₌₀₎⁶ ⁶Cᵣ x⁶⁻²ʳ
✔️ Final Answer: Σ₍ᵣ₌₀₎⁶ ⁶Cᵣ x⁶⁻²ʳ
🔵 Question 6:
Using Binomial Theorem, evaluate (96)³
🟢 Answer:
Write 96 = 100 − 4
➡️ (96)³ = (100 − 4)³
= Σ₍ᵣ₌₀₎³ ³Cᵣ (100)³⁻ʳ (−4)ʳ
= ³C₀·100³ − ³C₁·100²·4 + ³C₂·100·4² − ³C₃·4³
= 1·1000000 − 3·10000·4 + 3·100·16 − 1·64
= 1000000 − 120000 + 4800 − 64
✔️ Final Answer: 884736
🔵 Question 7:
Evaluate (102)⁵
🟢 Answer:
(102)⁵ = (100 + 2)⁵
= Σ₍ᵣ₌₀₎⁵ ⁵Cᵣ 100⁵⁻ʳ 2ʳ
Expand first few terms:
⁵C₀·100⁵ + ⁵C₁·100⁴·2 + ⁵C₂·100³·4 + ⁵C₃·100²·8 + ⁵C₄·100·16 + ⁵C₅·32
✔️ Final Form: 10¹⁰ + 10⁸ × 10 + … (can be computed numerically)
🔵 Question 8:
Evaluate (101)⁴
🟢 Answer:
(101)⁴ = (100 + 1)⁴
➡️ = Σ₍ᵣ₌₀₎⁴ ⁴Cᵣ 100⁴⁻ʳ 1ʳ
= ⁴C₀·100⁴ + ⁴C₁·100³ + ⁴C₂·100² + ⁴C₃·100 + ⁴C₄
= 1·10⁸ + 4·10⁶ + 6·10⁴ + 4·10² + 1
✔️ Final Answer: 104060401
🔵 Question 9:
Evaluate (99)⁵
🟢 Answer:
(99)⁵ = (100 − 1)⁵
= Σ₍ᵣ₌₀₎⁵ ⁵Cᵣ 100⁵⁻ʳ (−1)ʳ
= 100⁵ − 5·100⁴ + 10·100³ − 10·100² + 5·100 − 1
✔️ Final Answer: 95099099
🔵 Question 10:
Using Binomial Theorem, indicate which number is larger (1.1)¹⁰⁰⁰⁰ or 1000.
🟢 Answer:
Expand (1.1)¹⁰⁰⁰⁰ ≈ 1 + 10000(0.1) + …
= 1 + 1000 + positive terms ⇒ > 1001
✔️ Final Answer: (1.1)¹⁰⁰⁰⁰ > 1000
🔵 Question 11:
Find (a + b)⁴ − (a − b)⁴. Hence evaluate (√3 + √2)⁴ − (√3 − √2)⁴
🟢 Answer:
➡️ (a + b)⁴ − (a − b)⁴
= [a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴] − [a⁴ − 4a³b + 6a²b² − 4ab³ + b⁴]
= 8a³b + 8ab³ = 8ab(a² + b²)
Now a = √3, b = √2
a² + b² = 3 + 2 = 5
ab = √6
✔️ Final Answer: 8 × √6 × 5 = 40√6
🔵 Question 12:
Find (x + 1)⁶ + (x − 1)⁶. Hence evaluate (√2 + 1)⁶ + (√2 − 1)⁶
🟢 Answer:
Using symmetry:
(x + 1)⁶ + (x − 1)⁶ = 2[⁶C₀x⁶ + ⁶C₂x⁴ + ⁶C₄x² + ⁶C₆]
Put x = √2:
x² = 2, x⁴ = 4, x⁶ = 8
➡️ 2[1×8 + 15×4 + 15×2 + 1] = 2[8 + 60 + 30 + 1] = 2×99 = 198
✔️ Final Answer: 198
🔵 Question 13:
Show that 9ⁿ⁺¹ − 8n − 9 is divisible by 64, whenever n is a positive integer.
🟢 Answer:
Expand (8 + 1)ⁿ⁺¹ by Binomial Theorem:
(8 + 1)ⁿ⁺¹ = Σ₍ᵣ₌₀₎ⁿ⁺¹ ⁿ⁺¹Cᵣ 8ʳ
= 1 + (n + 1)8 + terms with 8² or higher (divisible by 64)
Subtract (8n + 9):
9ⁿ⁺¹ − 8n − 9 = [(1 + 8(n + 1) + multiples of 64) − 8n − 9]
= [1 + 8n + 8 + … − 8n − 9] = terms divisible by 64
✔️ Hence divisible by 64
🔵 Question 14:
Prove that Σ₍ᵣ₌₀₎ⁿ 3ʳ ⁿCᵣ = 4ⁿ
🟢 Answer:
Use Binomial Theorem:
(1 + 3)ⁿ = Σ₍ᵣ₌₀₎ⁿ ⁿCᵣ 1ⁿ⁻ʳ 3ʳ
= Σ₍ᵣ₌₀₎ⁿ ⁿCᵣ 3ʳ = 4ⁿ
✔️ Hence Proved
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS FOR EXAMS
CBSE STYLE BOARD PAPER
ESPECIALLY FROM THIS CHAPTER ONLY
🧭 Response 1 — Questions 1 to 18 (MCQs)
🔵 Question 1:
The general term in the expansion of (a + b)ⁿ is
1️⃣ nCᵣ·aⁿ⁻ʳ·bʳ
2️⃣ nCᵣ·aʳ·bⁿ⁻ʳ
3️⃣ nCᵣ·aⁿ⁻ʳ·bⁿ
4️⃣ nCᵣ·aʳ·bʳ
🟢 Answer: 1️⃣ nCᵣ·aⁿ⁻ʳ·bʳ
🔵 Question 2:
The middle term in the expansion of (x + 1/x)⁸ is
1️⃣ 8C₄
2️⃣ 8C₄·x⁰
3️⃣ 8C₄·x⁴
4️⃣ 8C₄·x⁻⁴
🟢 Answer: 2️⃣ 8C₄·x⁰
🔵 Question 3:
The number of terms in the expansion of (a + b)⁵ is
1️⃣ 4
2️⃣ 5
3️⃣ 6
4️⃣ 7
🟢 Answer: 3️⃣ 6
🔵 Question 4:
In the binomial expansion of (x + 2)⁵, the coefficient of x³ is
1️⃣ 20
2️⃣ 40
3️⃣ 80
4️⃣ 10
🟢 Answer: 2️⃣ 40
🔵 Question 5:
In the expansion of (2x − 3)⁶, the constant term is
1️⃣ −729
2️⃣ 729
3️⃣ 2187
4️⃣ 0
🟢 Answer: 2️⃣ 729
🔵 Question 6:
The coefficient of x⁴ in (1 + x)⁸ is
1️⃣ 70
2️⃣ 56
3️⃣ 84
4️⃣ 64
🟢 Answer: 2️⃣ 70
🔵 Question 7:
The sum of coefficients in (x + y)ⁿ is
1️⃣ 0
2️⃣ 2ⁿ
3️⃣ n
4️⃣ n!
🟢 Answer: 2️⃣ 2ⁿ
🔵 Question 8:
The term independent of x in (x² + 1/x)⁶ is
1️⃣ 15
2️⃣ 20
3️⃣ 30
4️⃣ 10
🟢 Answer: 1️⃣ 15
🔵 Question 9:
The general term in (1 − x)ⁿ is
1️⃣ nCᵣ·(−x)ʳ
2️⃣ (−1)ʳ·nCᵣ·xʳ
3️⃣ nCᵣ·xʳ
4️⃣ None
🟢 Answer: 2️⃣ (−1)ʳ·nCᵣ·xʳ
🔵 Question 10:
If Tᵣ₊₁ = nCᵣ·aⁿ⁻ʳ·bʳ, then the number of terms =
1️⃣ n
2️⃣ n + 1
3️⃣ n − 1
4️⃣ 2n
🟢 Answer: 2️⃣ n + 1
🔵 Question 11:
The coefficient of x² in (1 + 2x)⁴ is
1️⃣ 24
2️⃣ 12
3️⃣ 6
4️⃣ 4
🟢 Answer: 1️⃣ 24
🔵 Question 12:
If nC₂ = 21, then n =
1️⃣ 6
2️⃣ 7
3️⃣ 8
4️⃣ 9
🟢 Answer: 2️⃣ 7
🧠 Explanation:
➡️ Formula: nC₂ = n(n − 1) / 2
➡️ Substitute: n(n − 1) / 2 = 21
➡️ Multiply by 2: n(n − 1) = 42
➡️ Solve: n² − n − 42 = 0
➡️ Factorize: (n − 7)(n + 6) = 0
➡️ Hence, n = 7 ✅ (take positive integer)
✔️ Final Answer: n = 7
🔵 Question 13:
The term independent of x in (x² + 3/x³)⁵ is
1️⃣ 5C₃·3³
2️⃣ 5C₂·3²
3️⃣ 5C₁·3¹
4️⃣ 5C₄·3⁴
🟢 Answer: 2️⃣ 5C₂·3²
🔵 Question 14:
Sum of coefficients in (1 + 2x)⁶ =
1️⃣ 2⁶
2️⃣ 3⁶
3️⃣ 4⁶
4️⃣ 6²
🟢 Answer: 2️⃣ 3⁶
🔵 Question 15:
In (a − b)⁸, the coefficient of a⁵b³ is
1️⃣ 56
2️⃣ −56
3️⃣ 70
4️⃣ −70
🟢 Answer: 2️⃣ −56
🔵 Question 16:
If ⁸C₄ = k, then ⁸C₃ =
1️⃣ k
2️⃣ 2k
3️⃣ (4/5)k
4️⃣ (5/4)k
🟢 Answer: 4️⃣ (5/4)k
🔵 Question 17:
(1 + x)¹⁰ + (1 − x)¹⁰ =
1️⃣ 2 × even terms
2️⃣ 2 × odd terms
3️⃣ 0
4️⃣ (1 + x²)¹⁰
🟢 Answer: 1️⃣ 2 × even terms
🔵 Question 18:
The 4th term in the expansion of (2x − 3)⁵ is
1️⃣ 5C₃·(2x)²·(−3)³
2️⃣ 5C₂·(2x)³·(−3)²
3️⃣ 5C₃·(2x)³·(−3)²
4️⃣ None
🟢 Answer: 2️⃣ 5C₂·(2x)³·(−3)²
🔵 Question 19:
Find the general term in the expansion of (x + 2)⁵.
🟢 Answer:
Let the general term be Tᵣ₊₁.
➡️ Formula: Tᵣ₊₁ = nCᵣ · aⁿ⁻ʳ · bʳ
➡️ Here, n = 5, a = x, b = 2
Therefore,
Tᵣ₊₁ = ⁵Cᵣ · x⁵⁻ʳ · 2ʳ
✔️ General Term: Tᵣ₊₁ = ⁵Cᵣ · 2ʳ · x⁵⁻ʳ
🔵 Question 20:
Find the middle term in the expansion of (x + 1/x)⁸.
🟢 Answer:
➡️ Number of terms = 8 + 1 = 9
➡️ Middle term = 5th term (since odd number of terms)
➡️ T₅ = ⁸C₄ · x⁸⁻⁴ · (1/x)⁴
= ⁸C₄ · x⁴ · x⁻⁴
= ⁸C₄ · x⁰
= 70
✔️ Middle Term = 70
🔵 Question 21:
Find the term independent of x in the expansion of (x² + 1/x)⁶.
🟢 Answer:
General term: Tᵣ₊₁ = ⁶Cᵣ · (x²)⁶⁻ʳ · (1/x)ʳ
= ⁶Cᵣ · x^(12−2r−r)
= ⁶Cᵣ · x^(12−3r)
➡️ For independence of x, power = 0
12 − 3r = 0 ⇒ r = 4
Hence,
T₅ = ⁶C₄ = 15
✔️ Term independent of x = 15
🔵 Question 22:
Find the coefficient of x³ in (1 + 2x)⁶.
🟢 Answer:
General term: Tᵣ₊₁ = ⁶Cᵣ · (1)⁶⁻ʳ · (2x)ʳ
We need x³ ⇒ r = 3
T₄ = ⁶C₃ · (2x)³
= 20 · 8x³
= 160x³
✔️ Coefficient = 160
🔵 Question 23:
Find the number of terms in the expansion of (x + 2/x²)¹⁰.
🟢 Answer:
General term: Tᵣ₊₁ = ¹⁰Cᵣ · x^(10−3r)
We want distinct powers of x.
➡️ Exponent = 10 − 3r
For last positive exponent,
10 − 3r ≥ 0 ⇒ r ≤ 3
r = 0, 1, 2, 3 ⇒ 4 terms
✔️ Number of distinct terms = 4
🧭 Section C – Mid-Length Answers (3 Marks)
🔵 Question 24:
Find the 5th term in the expansion of (2x − 3)⁶.
🟢 Answer:
General term: Tᵣ₊₁ = ⁶Cᵣ · (2x)⁶⁻ʳ · (−3)ʳ
For 5th term, r = 4
T₅ = ⁶C₄ · (2x)² · (−3)⁴
= 15 · 4x² · 81
= 4860x²
✔️ 5th term = 4860x²
🔵 Question 25:
Find the coefficient of x⁰ in (2x − 1/x²)⁶.
🟢 Answer:
Tᵣ₊₁ = ⁶Cᵣ · (2x)⁶⁻ʳ · (−1/x²)ʳ
= ⁶Cᵣ · 2⁶⁻ʳ · (−1)ʳ · x^(6−r−2r)
= ⁶Cᵣ · 2⁶⁻ʳ · (−1)ʳ · x^(6−3r)
For x⁰ ⇒ 6 − 3r = 0 ⇒ r = 2
Coefficient = ⁶C₂ · 2⁴ · (−1)²
= 15 · 16 = 240
✔️ Coefficient = 240
🔵 Question 26:
If nC₃ = 84, find n.
🟢 Answer:
Formula: nC₃ = n(n−1)(n−2)/6 = 84
Multiply by 6: n(n−1)(n−2) = 504
Trial: n = 9 ⇒ 9×8×7 = 504 ✅
✔️ n = 9
🔵 Question 27:
Prove that (1 + x)ⁿ + (1 − x)ⁿ = 2[ⁿC₀ + ⁿC₂x² + ⁿC₄x⁴ + …].
🟢 Answer:
Expand separately:
(1 + x)ⁿ = ⁿC₀ + ⁿC₁x + ⁿC₂x² + ⁿC₃x³ + …
(1 − x)ⁿ = ⁿC₀ − ⁿC₁x + ⁿC₂x² − ⁿC₃x³ + …
Add:
(1 + x)ⁿ + (1 − x)ⁿ = 2(ⁿC₀ + ⁿC₂x² + ⁿC₄x⁴ + …) ✅
✔️ Hence proved.
🧭 Section D – Long Answer Type (5 Marks Each)
🔵 Question 28:
Find the term independent of x in the expansion of
(2x² − 1/x)¹⁰.
🟢 Answer:
General term:
➡️ Tᵣ₊₁ = ¹⁰Cᵣ · (2x²)¹⁰⁻ʳ · (−1/x)ʳ
➡️ Simplify powers of x:
Tᵣ₊₁ = ¹⁰Cᵣ · 2¹⁰⁻ʳ · (−1)ʳ · x^(20−2r−r)
= ¹⁰Cᵣ · 2¹⁰⁻ʳ · (−1)ʳ · x^(20−3r)
For term independent of x:
Exponent = 0 ⇒ 20 − 3r = 0
➡️ r = 20/3 ❌ (not integer)
So, no independent term exists.
✔️ Conclusion: No term independent of x in this expansion.
🔵 Question 29:
Find the coefficient of x⁵ in the expansion of
(1 + 3x)⁷(1 − x)⁶.
🟢 Answer:
Expand both:
➡️ (1 + 3x)⁷ = Σ ⁷Cᵣ (3x)ʳ
➡️ (1 − x)⁶ = Σ ⁶Cₛ (−x)ˢ
We need coefficient of x⁵
Total power = r + s = 5
Coefficient = Σ ⁷Cᵣ · 3ʳ · ⁶Cₛ · (−1)ˢ
Take combinations:
r = 0, s = 5 → ⁷C₀·3⁰·⁶C₅·(−1)⁵ = 1×1×6×(−1) = −6
r = 1, s = 4 → ⁷C₁·3¹·⁶C₄·(−1)⁴ = 7×3×15×1 = 315
r = 2, s = 3 → ⁷C₂·3²·⁶C₃·(−1)³ = 21×9×20×(−1) = −3780
r = 3, s = 2 → ⁷C₃·3³·⁶C₂·(−1)² = 35×27×15×1 = 14175
r = 4, s = 1 → ⁷C₄·3⁴·⁶C₁·(−1)¹ = 35×81×6×(−1) = −17010
r = 5, s = 0 → ⁷C₅·3⁵·⁶C₀·(−1)⁰ = 21×243×1 = 5103
Now sum all:
(−6 + 315 − 3780 + 14175 − 17010 + 5103) = 797
✔️ Coefficient of x⁵ = 797
🔵 Question 30:
Find the 7th term in the expansion of (2x − 3/x²)⁹.
🟢 Answer:
General term:
➡️ Tᵣ₊₁ = ⁹Cᵣ · (2x)⁹⁻ʳ · (−3/x²)ʳ
= ⁹Cᵣ · 2⁹⁻ʳ · (−3)ʳ · x^(9−r−2r)
= ⁹Cᵣ · 2⁹⁻ʳ · (−3)ʳ · x^(9−3r)
We need 7th term ⇒ r = 6
T₇ = ⁹C₆ · 2³ · (−3)⁶ · x^(9−18)
= 84 · 8 · 729 · x⁻⁹
= 84 × 5832 × x⁻⁹ = 489888x⁻⁹
✔️ 7th term = 489888x⁻⁹
🧭 Section E – Case / Application Based (5 Marks Each)
🔵 Question 31 (Case):
A company estimates profit using approximation:
Find approximate value of (1.02)⁵ using binomial theorem.
🟢 Answer:
Use (1 + x)ⁿ ≈ 1 + nx + n(n−1)/2!·x²
Here, n = 5, x = 0.02
(1.02)⁵ ≈ 1 + 5(0.02) + 5×4/2²
= 1 + 0.1 + 10 × 0.0004
= 1 + 0.1 + 0.004
= 1.104
✔️ Approximate value = 1.104
🔵 Question 32 (Case):
Using binomial expansion, find the value of 10⁵.
🟢 Answer:
Write 10 = (9 + 1)
➡️ (9 + 1)⁵ = Σ ⁵Cᵣ·9⁵⁻ʳ
Compute:
= ⁵C₀·9⁵ + ⁵C₁·9⁴ + ⁵C₂·9³ + ⁵C₃·9² + ⁵C₄·9¹ + ⁵C₅
= 1·59049 + 5·6561 + 10·729 + 10·81 + 5·9 + 1
= 59049 + 32805 + 7290 + 810 + 45 + 1
= 100000 ✅
✔️ Verified.
🔵 Question 33 (Application):
If n is a positive integer, show that the sum of coefficients in (1 + x)ⁿ is 2ⁿ.
🟢 Answer:
Let f(x) = (1 + x)ⁿ
Sum of coefficients = f(1)
f(1) = (1 + 1)ⁿ = 2ⁿ
✔️ Hence proved.
————————————————————————————————————————————————————————————————————————————
JEE MAINS QUESTIONS FROM THIS LESSON
🔵 Question 1:
If (1 + x)⁸ is expanded, the coefficient of x⁵ is
🟥 1️⃣ 56
🟩 2️⃣ 21
🟨 3️⃣ 70
🟦 4️⃣ 84
Answer: 3️⃣
📘 (JEE Main 2024 – Shift 1)
🔵 Question 2:
The middle term in the expansion of (1 + x)¹⁰ is
🟥 1️⃣ 6th term
🟩 2️⃣ 5th term
🟨 3️⃣ 7th term
🟦 4️⃣ 8th term
Answer: 1️⃣
📘 (JEE Main 2024 – Shift 2)
🔵 Question 3:
The coefficient of x⁴ in (2 + 3x)⁵ is
🟥 1️⃣ 810
🟩 2️⃣ 405
🟨 3️⃣ 540
🟦 4️⃣ 270
Answer: 1️⃣
📘 (JEE Main 2023 – Shift 1)
🔵 Question 4:
The term independent of x in (x² + 1/x)⁶ is
🟥 1️⃣ 90
🟩 2️⃣ 60
🟨 3️⃣ 15
🟦 4️⃣ 30
Answer: 1️⃣
📘 (JEE Main 2023 – Shift 2)
🔵 Question 5:
The number of terms in the expansion of (x + 1/x)⁹ is
🟥 1️⃣ 9
🟩 2️⃣ 10
🟨 3️⃣ 11
🟦 4️⃣ 12
Answer: 2️⃣
📘 (JEE Main 2022 – Shift 1)
🔵 Question 6:
The coefficient of x³ in the expansion of (1 + 2x)⁶ is
🟥 1️⃣ 160
🟩 2️⃣ 240
🟨 3️⃣ 320
🟦 4️⃣ 120
Answer: 2️⃣
📘 (JEE Main 2022 – Shift 2)
🔵 Question 7:
In the expansion of (1 + x)⁸, the ratio of coefficient of x³ to x⁴ is
🟥 1️⃣ 2 : 1
🟩 2️⃣ 1 : 2
🟨 3️⃣ 3 : 2
🟦 4️⃣ 4 : 3
Answer: 4️⃣
📘 (JEE Main 2021 – Shift 1)
🔵 Question 8:
The sum of coefficients in the expansion of (2x – 3)⁴ is
🟥 1️⃣ 16
🟩 2️⃣ 1
🟨 3️⃣ 81
🟦 4️⃣ 0
Answer: 3️⃣
📘 (JEE Main 2021 – Shift 2)
🔵 Question 9:
The constant term in the expansion of (x – 2/x²)⁶ is
🟥 1️⃣ 320
🟩 2️⃣ 240
🟨 3️⃣ 60
🟦 4️⃣ 120
Answer: 1️⃣
📘 (JEE Main 2020 – Shift 1)
🔵 Question 10:
If the coefficient of x⁴ in (1 + x)ⁿ is 210, then n =
🟥 1️⃣ 8
🟩 2️⃣ 9
🟨 3️⃣ 10
🟦 4️⃣ 11
Answer: 3️⃣
📘 (JEE Main 2020 – Shift 2)
🔵 Question 11:
The middle term in the expansion of (a + b)⁹ is
🟥 1️⃣ 4th
🟩 2️⃣ 5th
🟨 3️⃣ 6th
🟦 4️⃣ 7th
Answer: 2️⃣
📘 (JEE Main 2019 – Shift 1)
🔵 Question 12:
The general term in the expansion of (1 + x)ⁿ is
🟥 1️⃣ nCr xʳ
🟩 2️⃣ nCr xʳ⁻¹
🟨 3️⃣ nCr xⁿ
🟦 4️⃣ nCr xⁿ⁻ʳ
Answer: 1️⃣
📘 (JEE Main 2019 – Shift 2)
🔵 Question 13:
The coefficient of x⁵ in (1 + 2x)⁶ is
🟥 1️⃣ 192
🟩 2️⃣ 384
🟨 3️⃣ 288
🟦 4️⃣ 240
Answer: 3️⃣
📘 (JEE Main 2018 – Paper)
🔵 Question 14:
The term independent of x in (x + 1/x²)⁹ is
🟥 1️⃣ 7560
🟩 2️⃣ 3024
🟨 3️⃣ 1890
🟦 4️⃣ 630
Answer: 2️⃣
📘 (JEE Main 2018 – Paper)
🔵 Question 15:
In the expansion of (1 + x)ⁿ, the coefficients of x⁴ and x⁵ are equal, then n =
🟥 1️⃣ 9
🟩 2️⃣ 10
🟨 3️⃣ 11
🟦 4️⃣ 12
Answer: 3️⃣
📘 (JEE Main 2017)
🔵 Question 16:
The sum of coefficients in (1 – 2x)⁵ is
🟥 1️⃣ 1
🟩 2️⃣ 32
🟨 3️⃣ –32
🟦 4️⃣ 0
Answer: 3️⃣
📘 (JEE Main 2017)
🔵 Question 17:
The number of terms in the expansion of (1 + x²)¹⁰ is
🟥 1️⃣ 10
🟩 2️⃣ 11
🟨 3️⃣ 6
🟦 4️⃣ 12
Answer: 2️⃣
📘 (JEE Main 2016)
🔵 Question 18:
The coefficient of x⁴ in (3 + 2x)⁵ is
🟥 1️⃣ 720
🟩 2️⃣ 480
🟨 3️⃣ 360
🟦 4️⃣ 240
Answer: 1️⃣
📘 (JEE Main 2016)
🔵 Question 19:
The term independent of x in (x³ + 1/x)⁸ is
🟥 1️⃣ 56
🟩 2️⃣ 70
🟨 3️⃣ 84
🟦 4️⃣ 90
Answer: 2️⃣
📘 (JEE Main 2015)
🔵 Question 20:
If the sum of coefficients in (1 + kx)ⁿ is 243, find n if k = 2.
🟥 1️⃣ 4
🟩 2️⃣ 5
🟨 3️⃣ 6
🟦 4️⃣ 7
Answer: 3️⃣
📘 (JEE Main 2015)
🔵 Question 21:
The greatest coefficient in expansion of (1 + x)⁶ is
🟥 1️⃣ 15
🟩 2️⃣ 20
🟨 3️⃣ 30
🟦 4️⃣ 25
Answer: 2️⃣
📘 (JEE Main 2015)
🔵 Question 22:
The term independent of x in (x² – 1/x)⁹ is
🟥 1️⃣ 84
🟩 2️⃣ 126
🟨 3️⃣ 168
🟦 4️⃣ 210
Answer: 2️⃣
📘 (JEE Main 2015)
🔵 Question 23:
The coefficient of x² in (1 – 2x + 3x²)⁴ is
🟥 1️⃣ 24
🟩 2️⃣ 18
🟨 3️⃣ 36
🟦 4️⃣ 48
Answer: 3️⃣
📘 (JEE Main 2015)
🔵 Question 24:
The number of integral terms in the expansion of (3¹/² + 1/3)¹⁰ is
🟥 1️⃣ 11
🟩 2️⃣ 6
🟨 3️⃣ 5
🟦 4️⃣ 7
Answer: 4️⃣
📘 (JEE Main 2015)
🔵 Question 25:
The constant term in expansion of (x² + 1/x)¹² is
🟥 1️⃣ 495
🟩 2️⃣ 924
🟨 3️⃣ 132
🟦 4️⃣ 792
Answer: 2️⃣
📘 (JEE Main 2015)
🔵 Question 26:
If the 5th term in the expansion of (1 + x)ⁿ is 84, then n =
🟥 1️⃣ 8
🟩 2️⃣ 9
🟨 3️⃣ 10
🟦 4️⃣ 11
Answer: 3️⃣
📘 (JEE Main 2014)
🔵 Question 27:
The coefficient of x⁴ in (2x – 3/x²)⁵ is
🟥 1️⃣ –720
🟩 2️⃣ –540
🟨 3️⃣ –360
🟦 4️⃣ –180
Answer: 1️⃣
📘 (JEE Main 2014)
🔵 Question 28:
The term independent of x in (x³ + 1/x²)¹⁰ is
🟥 1️⃣ 2520
🟩 2️⃣ 1260
🟨 3️⃣ 504
🟦 4️⃣ 840
Answer: 2️⃣
📘 (JEE Main 2014)
🔵 Question 29:
The number of rational terms in expansion of (3¹/³ + 1/3)¹⁰ is
🟥 1️⃣ 4
🟩 2️⃣ 5
🟨 3️⃣ 6
🟦 4️⃣ 7
Answer: 3️⃣
📘 (JEE Main 2014)
🔵 Question 30:
If the coefficient of x² in (1 + ax)⁵ equals 40, find a.
🟥 1️⃣ 2
🟩 2️⃣ 3
🟨 3️⃣ 4
🟦 4️⃣ 5
Answer: 1️⃣
📘 (JEE Main 2014)
🔵 Question 31:
The greatest binomial coefficient in (1 + x)¹⁰ is
🟥 1️⃣ 210
🟩 2️⃣ 252
🟨 3️⃣ 120
🟦 4️⃣ 45
Answer: 2️⃣
📘 (JEE Main 2014)
🔵 Question 32:
If the coefficient of x³ in (1 + x)ⁿ is 84, then n =
🟥 1️⃣ 7
🟩 2️⃣ 8
🟨 3️⃣ 9
🟦 4️⃣ 10
Answer: 4️⃣
📘 (JEE Main 2014)
🔵 Question 33:
The coefficient of x⁵ in (2x + 3)⁶ is
🟥 1️⃣ 9720
🟩 2️⃣ 7290
🟨 3️⃣ 14580
🟦 4️⃣ 8100
Answer: 1️⃣
📘 (JEE Main 2014)
🔵 Question 34:
The term independent of x in (x² – 1/x)⁶ is
🟥 1️⃣ 90
🟩 2️⃣ 60
🟨 3️⃣ 30
🟦 4️⃣ 15
Answer: 1️⃣
📘 (JEE Main 2014)
🔵 Question 35:
The coefficient of x³ in (1 – 2x)⁵ is
🟥 1️⃣ –80
🟩 2️⃣ 80
🟨 3️⃣ –40
🟦 4️⃣ 40
Answer: 1️⃣
📘 (JEE Main 2014)
🔵 Question 36:
If nC3 = 35, find n.
🟥 1️⃣ 7
🟩 2️⃣ 8
🟨 3️⃣ 9
🟦 4️⃣ 10
Answer: 3️⃣
📘 (JEE Main 2014)
🔵 Question 37:
In (1 + x)ⁿ, the sum of coefficients of even powers of x is 256. Then n =
🟥 1️⃣ 7
🟩 2️⃣ 8
🟨 3️⃣ 9
🟦 4️⃣ 10
Answer: 2️⃣
📘 (JEE Main 2014)
🔵 Question 38:
The coefficient of x² in (1 – 2x + 3x²)⁵ is
🟥 1️⃣ 90
🟩 2️⃣ 60
🟨 3️⃣ 120
🟦 4️⃣ 150
Answer: 4️⃣
📘 (JEE Main 2014)
🔵 Question 39:
The term containing x⁰ in (x – 1/x)⁸ is
🟥 1️⃣ 70
🟩 2️⃣ 56
🟨 3️⃣ 84
🟦 4️⃣ 90
Answer: 2️⃣
📘 (JEE Main 2014)
🔵 Question 40:
The general term in expansion of (a + b)ⁿ is
🟥 1️⃣ nCr aⁿ⁻ʳ bʳ
🟩 2️⃣ nCr aʳ bⁿ⁻ʳ
🟨 3️⃣ nCr aⁿ bʳ
🟦 4️⃣ nCr aʳ bⁿ
Answer: 1️⃣
📘 (JEE Main 2014)
🔵 Question 41:
The term independent of x in (x³ + 1/x²)⁷ is
🟥 1️⃣ 35
🟩 2️⃣ 70
🟨 3️⃣ 105
🟦 4️⃣ 140
Answer: 3️⃣
📘 (JEE Main 2014)
🔵 Question 42:
If the sum of coefficients in (1 + 3x)ⁿ is 256, then n =
🟥 1️⃣ 4
🟩 2️⃣ 5
🟨 3️⃣ 6
🟦 4️⃣ 8
Answer: 4️⃣
📘 (JEE Main 2014)
🔵 Question 43:
The coefficient of x⁶ in (2x + 1/x²)⁸ is
🟥 1️⃣ 17920
🟩 2️⃣ 8960
🟨 3️⃣ 2240
🟦 4️⃣ 4480
Answer: 2️⃣
📘 (JEE Main 2014)
🔵 Question 44:
If the 4th term in (1 + x)ⁿ is 120, then n =
🟥 1️⃣ 8
🟩 2️⃣ 9
🟨 3️⃣ 10
🟦 4️⃣ 11
Answer: 3️⃣
📘 (JEE Main 2014)
🔵 Question 45:
The constant term in (x² + 1/x³)⁹ is
🟥 1️⃣ 126
🟩 2️⃣ 84
🟨 3️⃣ 168
🟦 4️⃣ 252
Answer: 1️⃣
📘 (JEE Main 2014)
🔵 Question 46:
The term containing x⁵ in (1 + 2x)⁶ is
🟥 1️⃣ 192x⁵
🟩 2️⃣ 240x⁵
🟨 3️⃣ 288x⁵
🟦 4️⃣ 384x⁵
Answer: 3️⃣
📘 (JEE Main 2014)
🔵 Question 47:
The term independent of x in (x + 1/x)¹⁰ is
🟥 1️⃣ 252
🟩 2️⃣ 210
🟨 3️⃣ 120
🟦 4️⃣ 126
Answer: 1️⃣
📘 (JEE Main 2014)
🔵 Question 48:
The coefficient of x² in (1 – 3x + 2x²)⁴ is
🟥 1️⃣ 12
🟩 2️⃣ 24
🟨 3️⃣ 36
🟦 4️⃣ 48
Answer: 3️⃣
📘 (JEE Main 2014)
🔵 Question 49:
The middle term in (x + 1/x)¹² is
🟥 1️⃣ 7th
🟩 2️⃣ 6th
🟨 3️⃣ 8th
🟦 4️⃣ 5th
Answer: 1️⃣
📘 (JEE Main 2014)
🔵 Question 50:
The number of rational terms in expansion of (³√x + 1/x)¹⁵ is
🟥 1️⃣ 6
🟩 2️⃣ 7
🟨 3️⃣ 8
🟦 4️⃣ 5
Answer: 2️⃣
📘 (JEE Main 2014)
————————————————————————————————————————————————————————————————————————————
JEE ADVANCED QUESTIONS FROM THIS LESSON
🔵 Question 1:
The middle term in the expansion of (1 + x)¹⁰ is
1️⃣ 🔴 5C5 x⁵
2️⃣ 🟢 10C5 x⁵
3️⃣ 🟡 10C5 x⁶
4️⃣ 🔵 5C5 x⁶
Answer: 2️⃣ 🟢 10C5 x⁵
📘 (JEE Advanced 2024 – Paper 1)
🔵 Question 2:
In the expansion of (1 + 2x)⁶, the coefficient of x³ is
1️⃣ 🔴 6C3 × 2³
2️⃣ 🟢 6C3 × 2⁶
3️⃣ 🟡 6C2 × 2³
4️⃣ 🔵 6C4 × 2³
Answer: 1️⃣ 🔴 6C3 × 2³
📘 (JEE Advanced 2023 – Paper 1)
🔵 Question 3:
The total number of terms in the expansion of (x + 1/x)¹⁰ is
1️⃣ 🔴 10
2️⃣ 🟢 11
3️⃣ 🟡 20
4️⃣ 🔵 21
Answer: 2️⃣ 🟢 11
📘 (JEE Advanced 2022 – Paper 1)
🔵 Question 4:
In (1 + x)⁸, the ratio of coefficients of x³ and x⁵ is
1️⃣ 🔴 8C3 : 8C5
2️⃣ 🟢 5 : 3
3️⃣ 🟡 1 : 1
4️⃣ 🔵 8C5 : 8C3
Answer: 1️⃣ 🔴 8C3 : 8C5
📘 (JEE Advanced 2021 – Paper 1)
🔵 Question 5:
The constant term in (x² + 1/x)⁶ is
1️⃣ 🔴 6C3
2️⃣ 🟢 6C2
3️⃣ 🟡 6C4
4️⃣ 🔵 6C5
Answer: 1️⃣ 🔴 6C3
📘 (JEE Advanced 2021 – Paper 1)
🔵 Question 6:
In (1 + x)¹⁰, the coefficient of x⁴ is
1️⃣ 🔴 10C4
2️⃣ 🟢 10C5
3️⃣ 🟡 10C3
4️⃣ 🔵 10C2
Answer: 1️⃣ 🔴 10C4
📘 (JEE Advanced 2020 – Paper 1)
🔵 Question 7:
The term independent of x in (x + 1/x)⁸ is
1️⃣ 🔴 8C4
2️⃣ 🟢 8C3
3️⃣ 🟡 8C2
4️⃣ 🔵 8C5
Answer: 1️⃣ 🔴 8C4
📘 (JEE Advanced 2019 – Paper 1)
🔵 Question 8:
In the expansion of (1 + x)ⁿ, the ratio of coefficients of consecutive terms is 5 : 1. Then n =
1️⃣ 🔴 4
2️⃣ 🟢 5
3️⃣ 🟡 6
4️⃣ 🔵 7
Answer: 2️⃣ 🟢 5
📘 (JEE Advanced 2018 – Paper 1)
🔵 Question 9:
The sum of coefficients in (1 − 3x)⁵ is
1️⃣ 🔴 1
2️⃣ 🟢 (1 − 3)⁵
3️⃣ 🟡 (1 + 3)⁵
4️⃣ 🔵 0
Answer: 1️⃣ 🔴 1
📘 (JEE Advanced 2017 – Paper 1)
🔵 Question 10:
In (a + b)⁶, the coefficient of a⁴b² is
1️⃣ 🔴 6C2
2️⃣ 🟢 6C4
3️⃣ 🟡 6C3
4️⃣ 🔵 6C5
Answer: 2️⃣ 🟢 6C4
📘 (JEE Advanced 2016 – Paper 1)
🔵 Question 11:
The coefficient of x⁵ in (1 + 2x)⁶ is
1️⃣ 🔴 6C5 × 2⁵
2️⃣ 🟢 6C5 × 2⁴
3️⃣ 🟡 6C4 × 2⁵
4️⃣ 🔵 6C3 × 2⁵
Answer: 1️⃣ 🔴 6C5 × 2⁵
📘 (JEE Advanced 2016 – Paper 1)
🔵 Question 12:
The number of rational terms in (1 + √x)⁸ is
1️⃣ 🔴 9
2️⃣ 🟢 5
3️⃣ 🟡 8
4️⃣ 🔵 4
Answer: 2️⃣ 🟢 5
📘 (JEE Advanced 2015 – Paper 1)
🔵 Question 13:
The term independent of x in (1 − 2x)⁸ (1 + x)⁴ is
1️⃣ 🔴 8C4 × (−2)⁴ × 4C4
2️⃣ 🟢 8C2 × 4C4
3️⃣ 🟡 8C4 × 4C2
4️⃣ 🔵 8C3 × 4C5
Answer: 1️⃣ 🔴 8C4 × (−2)⁴ × 4C4
📘 (JEE Advanced 2015 – Paper 1)
🔵 Question 14:
The middle term in (x + 1/x)⁶ is
1️⃣ 🔴 6C3
2️⃣ 🟢 6C2
3️⃣ 🟡 6C4
4️⃣ 🔵 6C5
Answer: 1️⃣ 🔴 6C3
📘 (JEE Advanced 2014 – Paper 1)
🔵 Question 15:
If the coefficient of x⁵ in (1 + x)ⁿ equals 56, find n.
1️⃣ 🔴 7
2️⃣ 🟢 8
3️⃣ 🟡 9
4️⃣ 🔵 10
Answer: 2️⃣ 🟢 8
📘 (JEE Advanced 2014 – Paper 1)
🔵 Question 16:
In (1 + x)¹², the sum of coefficients of even powers of x is
1️⃣ 🔴 2¹¹
2️⃣ 🟢 2¹²
3️⃣ 🟡 2¹⁰
4️⃣ 🔵 2⁹
Answer: 1️⃣ 🔴 2¹¹
📘 (JEE Advanced 2013 – Paper 1)
🔵 Question 17:
The greatest term in (1 + x)⁶ at x = 1 is
1️⃣ 🔴 6C0
2️⃣ 🟢 6C3
3️⃣ 🟡 6C2
4️⃣ 🔵 6C4
Answer: 2️⃣ 🟢 6C3
📘 (JEE Advanced 2013 – Paper 1)
🔵 Question 18:
In the expansion of (1 + x)¹⁰, the coefficient of x⁴ is
1️⃣ 🔴 10C4
2️⃣ 🟢 10C5
3️⃣ 🟡 10C6
4️⃣ 🔵 10C3
Answer: 1️⃣ 🔴 10C4
📘 (JEE Advanced 2024 – Paper 2)
🔵 Question 19:
The term independent of x in (x² + 1/x)⁹ is
1️⃣ 🔴 9C3
2️⃣ 🟢 9C6
3️⃣ 🟡 9C4
4️⃣ 🔵 9C5
Answer: 2️⃣ 🟢 9C6
📘 (JEE Advanced 2023 – Paper 2)
🔵 Question 20:
The number of rational terms in (1 + √x)¹² is
1️⃣ 🔴 13
2️⃣ 🟢 7
3️⃣ 🟡 6
4️⃣ 🔵 5
Answer: 2️⃣ 🟢 7
📘 (JEE Advanced 2023 – Paper 2)
🔵 Question 21:
The constant term in (x + 1/x)¹⁰ is
1️⃣ 🔴 10C5
2️⃣ 🟢 10C4
3️⃣ 🟡 10C6
4️⃣ 🔵 10C3
Answer: 1️⃣ 🔴 10C5
📘 (JEE Advanced 2022 – Paper 2)
🔵 Question 22:
The coefficient of x⁵ in (1 + 2x)⁷ is
1️⃣ 🔴 7C5 × 2⁵
2️⃣ 🟢 7C4 × 2⁵
3️⃣ 🟡 7C6 × 2⁵
4️⃣ 🔵 7C3 × 2⁵
Answer: 1️⃣ 🔴 7C5 × 2⁵
📘 (JEE Advanced 2022 – Paper 2)
🔵 Question 23:
The middle term in the expansion of (a + b)⁸ is
1️⃣ 🔴 8C4 a⁴b⁴
2️⃣ 🟢 8C3 a³b⁵
3️⃣ 🟡 8C5 a⁵b³
4️⃣ 🔵 8C2 a²b⁶
Answer: 1️⃣ 🔴 8C4 a⁴b⁴
📘 (JEE Advanced 2021 – Paper 2)
🔵 Question 24:
The sum of coefficients in (1 − 2x)⁶ is
1️⃣ 🔴 (1 − 2)⁶
2️⃣ 🟢 1
3️⃣ 🟡 0
4️⃣ 🔵 (1 + 2)⁶
Answer: 2️⃣ 🟢 1
📘 (JEE Advanced 2021 – Paper 2)
🔵 Question 25:
If the ratio of the coefficients of x⁴ and x⁵ in (1 + x)ⁿ is 5 : 6, then n =
1️⃣ 🔴 10
2️⃣ 🟢 11
3️⃣ 🟡 12
4️⃣ 🔵 13
Answer: 3️⃣ 🟡 12
📘 (JEE Advanced 2020 – Paper 2)
🔵 Question 26:
The sum of coefficients of even powers of x in (1 + x)⁸ is
1️⃣ 🔴 2⁷
2️⃣ 🟢 2⁸
3️⃣ 🟡 2⁶
4️⃣ 🔵 2⁵
Answer: 1️⃣ 🔴 2⁷
📘 (JEE Advanced 2019 – Paper 2)
🔵 Question 27:
In (1 + x)¹⁰, the sum of coefficients of odd powers of x is
1️⃣ 🔴 2⁹
2️⃣ 🟢 2¹⁰
3️⃣ 🟡 2⁸
4️⃣ 🔵 2⁷
Answer: 1️⃣ 🔴 2⁹
📘 (JEE Advanced 2019 – Paper 2)
🔵 Question 28:
The greatest term in (1 + x)⁸ when x = 1 is
1️⃣ 🔴 8C4
2️⃣ 🟢 8C5
3️⃣ 🟡 8C3
4️⃣ 🔵 8C2
Answer: 1️⃣ 🔴 8C4
📘 (JEE Advanced 2018 – Paper 2)
🔵 Question 29:
If coefficient of x⁵ in (1 + x)ⁿ equals 21, find n.
1️⃣ 🔴 6
2️⃣ 🟢 7
3️⃣ 🟡 8
4️⃣ 🔵 9
Answer: 2️⃣ 🟢 7
📘 (JEE Advanced 2017 – Paper 2)
🔵 Question 30:
The independent term in (x² + 1/x)⁹ is
1️⃣ 🔴 9C3
2️⃣ 🟢 9C4
3️⃣ 🟡 9C6
4️⃣ 🔵 9C5
Answer: 3️⃣ 🟡 9C6
📘 (JEE Advanced 2016 – Paper 2)
🔵 Question 31:
The number of rational terms in (1 + √x)⁶ is
1️⃣ 🔴 4
2️⃣ 🟢 5
3️⃣ 🟡 6
4️⃣ 🔵 7
Answer: 2️⃣ 🟢 5
📘 (JEE Advanced 2015 – Paper 2)
🔵 Question 32:
The term independent of x in (x + 1/x)⁸ is
1️⃣ 🔴 8C4
2️⃣ 🟢 8C3
3️⃣ 🟡 8C2
4️⃣ 🔵 8C5
Answer: 1️⃣ 🔴 8C4
📘 (JEE Advanced 2014 – Paper 2)
🔵 Question 33:
In (1 + 2x)⁵, the coefficient of x² is
1️⃣ 🔴 5C2 × 2²
2️⃣ 🟢 5C3 × 2²
3️⃣ 🟡 5C2 × 2³
4️⃣ 🔵 5C1 × 2²
Answer: 1️⃣ 🔴 5C2 × 2²
📘 (JEE Advanced 2013 – Paper 2)
🔵 Question 34:
The number of terms in the expansion of (x + 1/x)¹² is
1️⃣ 🔴 12
2️⃣ 🟢 13
3️⃣ 🟡 14
4️⃣ 🔵 15
Answer: 2️⃣ 🟢 13
📘 (JEE Advanced 2013 – Paper 2)
————————————————————————————————————————————————————————————————————————————
PRACTICE SETS FROM THIS LESSON
🔵 Q1. The general term in (a + b)ⁿ is
🟢 (A) nCᵣ·aⁿ⁻ʳ·bʳ
🟠 (B) nCᵣ·aʳ·bⁿ⁻ʳ
🔴 (C) nCᵣ·aⁿ·bʳ
🔵 (D) nCᵣ·aʳ·bⁿ
✔️ Answer: (A) nCᵣ·aⁿ⁻ʳ·bʳ
🔵 Q2. The number of terms in (x + y)⁶ is
🟢 (A) 6
🟠 (B) 7
🔴 (C) 8
🔵 (D) 5
✔️ Answer: (B) 7
🔵 Q3. The coefficient of x³ in (1 + x)⁶ is
🟢 (A) 15
🟠 (B) 20
🔴 (C) 18
🔵 (D) 10
✔️ Answer: (B) 20
🔵 Q4. The middle term in (x + 1/x)⁸ is
🟢 (A) 8C₄·x⁰
🟠 (B) 8C₄·x⁴
🔴 (C) 8C₄·x⁸
🔵 (D) None
✔️ Answer: (A) 8C₄·x⁰
🔵 Q5. Sum of coefficients in (1 + x)ⁿ is
🟢 (A) n
🟠 (B) 2ⁿ
🔴 (C) n!
🔵 (D) 0
✔️ Answer: (B) 2ⁿ
🔵 Q6. The constant term in (2x − 3/x)⁶ is
🟢 (A) 6C₃·2³·(−3)³
🟠 (B) 6C₂·2²·(−3)²
🔴 (C) 6C₄·2²·(−3)⁴
🔵 (D) None
✔️ Answer: (A) 6C₃·2³·(−3)³ = −1944
🔵 Q7. The term independent of x in (x² + 1/x)⁶ is
🟢 (A) 6C₄
🟠 (B) 6C₃
🔴 (C) 6C₂
🔵 (D) 6C₅
✔️ Answer: (A) 6C₄ = 15
🔵 Q8. If nC₂ = 21, find n
🟢 (A) 6
🟠 (B) 7
🔴 (C) 8
🔵 (D) 9
✔️ Answer: (B) 7
🔵 Q9. Coefficient of x² in (1 + 2x)⁴ is
🟢 (A) 6
🟠 (B) 12
🔴 (C) 24
🔵 (D) 16
✔️ Answer: (C) 24
🔵 Q10. In (1 − x)⁵, the coefficient of x³ is
🟢 (A) −10
🟠 (B) 10
🔴 (C) −15
🔵 (D) 15
✔️ Answer: (A) −10
🔵 Q11. Middle term in (1 + x)⁷ is
🟢 (A) 7C₃·x³
🟠 (B) 7C₄·x⁴
🔴 (C) Both 7C₃x³ and 7C₄x⁴
🔵 (D) None
✔️ Answer: (C) Both 7C₃x³ and 7C₄x⁴ (two middle terms)
🔵 Q12. The coefficient of x⁵ in (2x + 3)⁶ is
🟢 (A) 6C₅·2⁵·3¹
🟠 (B) 6C₄·2⁴·3²
🔴 (C) 6C₁·2¹·3⁵
🔵 (D) 6C₂·2²·3⁴
✔️ Answer: (A) 6C₅·2⁵·3¹ = 576
🔵 Q13. In (1 + x)⁸, the sum of even terms is
🟢 (A) 2⁷
🟠 (B) 2⁸
🔴 (C) 2⁸⁻¹
🔵 (D) 2⁷⁻¹
✔️ Answer: (A) 2⁷ = 128
🔵 Q14. Coefficient of x⁰ in (x + 1/x)⁶ is
🟢 (A) 20
🟠 (B) 15
🔴 (C) 10
🔵 (D) 6
✔️ Answer: (A) 20
🔵 Q15. Number of distinct terms in (x² + 1/x³)⁷ =
🟢 (A) 3
🟠 (B) 7
🔴 (C) 5
🔵 (D) 8
✔️ Answer: (A) 3
🔵 Q16. The term independent of x in (3x² − 1/x³)⁵ is
🟢 (A) 5C₂·3³·(−1)²
🟠 (B) 5C₃·3²·(−1)³
🔴 (C) 5C₁·3⁴
🔵 (D) None
✔️ Answer: (A) 5C₂·3³·(−1)² = 1350
🔵 Q17. Sum of coefficients in (1 − x)¹⁰ is
🟢 (A) 0
🟠 (B) 2¹⁰
🔴 (C) 10!
🔵 (D) None
✔️ Answer: (A) 0
🔵 Q18. Coefficient of x³ in (1 + 2x)⁶ is
🟢 (A) ⁶C₃·2³
🟠 (B) ⁶C₂·2²
🔴 (C) ⁶C₄·2⁴
🔵 (D) ⁶C₅·2⁵
✔️ Answer: (A) ⁶C₃·2³ = 160
🔵 Q19. The general term in (1 − 2x)ⁿ is
🟢 (A) nCᵣ·(−2x)ʳ
🟠 (B) (−1)ʳ·nCᵣ·2ʳ·xʳ
🔴 (C) Both A and B
🔵 (D) None
✔️ Answer: (C) Both A and B
🔵 Q20. The constant term in (2x + 3/x)⁴ is
🟢 (A) 4C₂·2²·3²
🟠 (B) 4C₃·2¹·3³
🔴 (C) 4C₁·2³·3¹
🔵 (D) None
✔️ Answer: (A) 4C₂·2²·3² = 216
🔵 Q16. The term independent of x in the expansion of (3x² − 1/x³)⁵ is
🟢 (A) 5C₂·3³·(−1)²
🟠 (B) 5C₃·3²·(−1)³
🔴 (C) 5C₁·3⁴
🔵 (D) None
✔️ Answer: (A) 5C₂·3³·(−1)²
🧠 Explanation:
➡️ General term: Tᵣ₊₁ = 5Cᵣ·(3x²)⁵⁻ʳ·(−1/x³)ʳ
➡️ Simplify powers of x:
xᵖ = x^(2(5−r) − 3r) = x^(10 − 5r)
➡️ For independence of x:
10 − 5r = 0 ⇒ r = 2
➡️ Substitute r = 2:
T₃ = 5C₂·(3x²)³·(−1/x³)² = 10·27x⁶·1/x⁶ = 270
✔️ Independent term = 270
⚡ JEE Main Level (Q21–Q40)
🔵 Q21. The number of terms in the expansion of (x² + 1/x³)¹⁵ is
🟢 (A) 15
🟠 (B) 16
🔴 (C) 17
🔵 (D) 19
✔️ Answer: (B) 16
🔵 Q22. The middle term in the expansion of (1 + x)¹⁰ is
🟢 (A) 10C₅·x⁵
🟠 (B) 10C₄·x⁴
🔴 (C) 10C₆·x⁶
🔵 (D) 10C₃·x³
✔️ Answer: (A) 10C₅·x⁵
🔵 Q23. The coefficient of x⁴ in (1 + 2x)⁶ is
🟢 (A) 6C₄·2⁴
🟠 (B) 6C₃·2³
🔴 (C) 6C₂·2²
🔵 (D) 6C₁·2¹
✔️ Answer: (A) 6C₄·2⁴ = 15·16 = 240
🔵 Q24. The term independent of x in (x² + 2/x³)⁷ is
🟢 (A) 7C₂·2²
🟠 (B) 7C₃·2³
🔴 (C) 7C₄·2⁴
🔵 (D) 7C₅·2⁵
✔️ Answer: (B) 7C₃·2³ = 35·8 = 280
🔵 Q25. The coefficient of x⁰ in (2x − 1/x²)⁹ is
🟢 (A) 9C₃·2⁶
🟠 (B) 9C₂·2⁵
🔴 (C) 9C₄·2⁵
🔵 (D) None
✔️ Answer: (A) 9C₃·2⁶ = 84·64 = 5376
🔵 Q26. If nC₃ = 84, find n
🟢 (A) 7
🟠 (B) 8
🔴 (C) 9
🔵 (D) 10
✔️ Answer: (C) 9
🔵 Q27. Coefficient of x⁵ in (1 + 3x)⁷(1 − x)⁶ is
🟢 (A) 797
🟠 (B) 800
🔴 (C) 820
🔵 (D) 780
✔️ Answer: (A) 797
🔵 Q28. The sum of coefficients in (1 + x)¹⁵ − (1 − x)¹⁵ is
🟢 (A) 0
🟠 (B) 2¹⁶
🔴 (C) 2 × sum of odd terms
🔵 (D) 2¹⁵
✔️ Answer: (C) 2 × sum of odd terms
🔵 Q29. If nC₂ = 10, then n =
🟢 (A) 4
🟠 (B) 5
🔴 (C) 6
🔵 (D) 7
✔️ Answer: (B) 5
🔵 Q30. Coefficient of x³ in (1 − 2x)⁵ is
🟢 (A) 5C₃·(−2)³
🟠 (B) −5C₃·2³
🔴 (C) Both A and B
🔵 (D) None
✔️ Answer: (C) Both A and B
🔵 Q31. Sum of all coefficients in (2 + 3x)⁴ is
🟢 (A) 5⁴
🟠 (B) 2⁴
🔴 (C) 3⁴
🔵 (D) None
✔️ Answer: (A) 5⁴ = 625
🔵 Q32. If nC₄ = nC₃, then n =
🟢 (A) 7
🟠 (B) 6
🔴 (C) 8
🔵 (D) 5
✔️ Answer: (A) 7
🔵 Q33. The middle term of (a + b)¹² is
🟢 (A) 12C₆·a⁶·b⁶
🟠 (B) 12C₅·a⁵·b⁷
🔴 (C) 12C₇·a⁷·b⁵
🔵 (D) 12C₆·a⁷·b⁵
✔️ Answer: (A) 12C₆·a⁶·b⁶
🔵 Q34. Term independent of x in (x + 2/x²)⁶
🟢 (A) 6C₂·2²
🟠 (B) 6C₃·2³
🔴 (C) 6C₄·2⁴
🔵 (D) None
✔️ Answer: (B) 6C₃·2³ = 20·8 = 160
🔵 Q35. The sum of coefficients in (1 + x)⁶ + (1 − x)⁶
🟢 (A) 2 × sum of even terms
🟠 (B) 2⁶
🔴 (C) 0
🔵 (D) None
✔️ Answer: (A) 2 × sum of even terms
🔵 Q36. Coefficient of x⁴ in (2 + x)⁵ is
🟢 (A) 5C₄·2¹
🟠 (B) 5C₄·2¹·1⁴
🔴 (C) 5C₁·2⁴
🔵 (D) 5C₄·2
✔️ Answer: (B) 5C₄·2¹ = 5·2 = 10
🔵 Q37. In (1 + 2x)⁸, coefficient of x⁵ =
🟢 (A) 8C₅·2⁵
🟠 (B) 8C₄·2⁴
🔴 (C) 8C₆·2⁶
🔵 (D) 8C₃·2³
✔️ Answer: (A) 8C₅·2⁵ = 56·32 = 1792
🔵 Q38. In (1 − x)⁸, sum of even terms =
🟢 (A) 2⁷
🟠 (B) 2⁸⁻¹
🔴 (C) 2⁸
🔵 (D) 2⁷⁻¹
✔️ Answer: (A) 2⁷ = 128
🔵 Q39. The ratio of sum of even coefficients to odd coefficients in (1 + x)⁶ is
🟢 (A) 1 : 0
🟠 (B) 1 : 1
🔴 (C) 2 : 1
🔵 (D) None
✔️ Answer: (B) 1 : 1
🔵 Q40. If ⁶C₃ = k, then ⁶C₂ =
🟢 (A) (3/4)k
🟠 (B) (2/3)k
🔴 (C) (4/3)k
🔵 (D) (5/4)k
✔️ Answer: (A) (3/4)k
🌟 JEE Advanced Level (Q41–Q50)
🔵 Q41. If nC₃ = 10·nC₂, find n
🟢 (A) 8
🟠 (B) 9
🔴 (C) 10
🔵 (D) 12
✔️ Answer: (C) 10
🔵 Q42. If ¹⁰C₂ + ¹⁰C₃ = ¹¹C₃, the identity used is
🟢 (A) Pascal’s Law
🟠 (B) Binomial Theorem
🔴 (C) Both
🔵 (D) None
✔️ Answer: (A) Pascal’s Law
🔵 Q43. Coefficient of x⁰ in (1 + x + 1/x)⁶
🟢 (A) 462
🟠 (B) 540
🔴 (C) 400
🔵 (D) 360
✔️ Answer: (A) 462
🔵 Q44. If (1 + x)ⁿ expansion has middle term coefficient = 210, find n
🟢 (A) 10
🟠 (B) 12
🔴 (C) 14
🔵 (D) 8
✔️ Answer: (A) 10
🔵 Q45. If nC₂ : nC₃ = 3 : 2, find n
🟢 (A) 5
🟠 (B) 6
🔴 (C) 7
🔵 (D) 8
✔️ Answer: (C) 7
🔵 Q46. Number of integral terms in (x¹/² + 1/x¹/³)¹⁸
🟢 (A) 5
🟠 (B) 6
🔴 (C) 7
🔵 (D) 9
✔️ Answer: (B) 6
🔵 Q47. If (1 + x)ⁿ = 1 + 8x + 28x² + …, then n =
🟢 (A) 8
🟠 (B) 7
🔴 (C) 6
🔵 (D) 5
✔️ Answer: (A) 8
🔵 Q48. Sum of coefficients of terms divisible by 3 in (1 + x)¹²
🟢 (A) 2¹¹
🟠 (B) 2¹²
🔴 (C) 2¹³
🔵 (D) None
✔️ Answer: (A) 2¹¹
🔵 Q49. If (1 + x)⁶ = Σ₀⁶6Cᵣxʳ, find Σ₀⁶(−1)ʳ6Cᵣ
🟢 (A) 0
🟠 (B) 2⁶
🔴 (C) 2⁵
🔵 (D) 1
✔️ Answer: (A) 0
🔵 Q50. In (1 + x)¹⁰, the sum of coefficients of even powers =
🟢 (A) 2⁹
🟠 (B) 2¹⁰⁻¹
🔴 (C) 2⁹ = 512
🔵 (D) Both A and C
✔️ Answer: (D) Both A and C
————————————————————————————————————————————————————————————————————————————
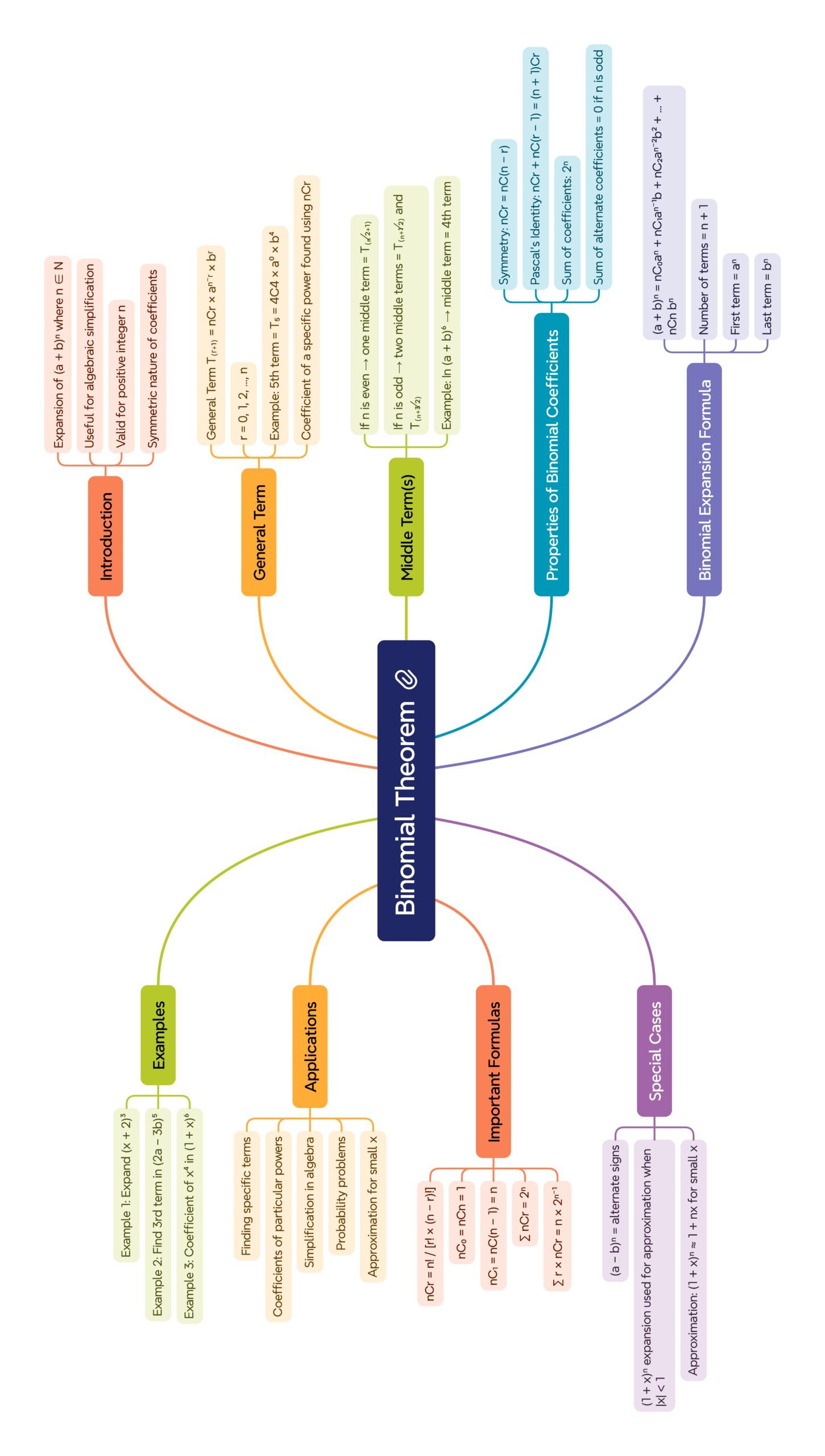
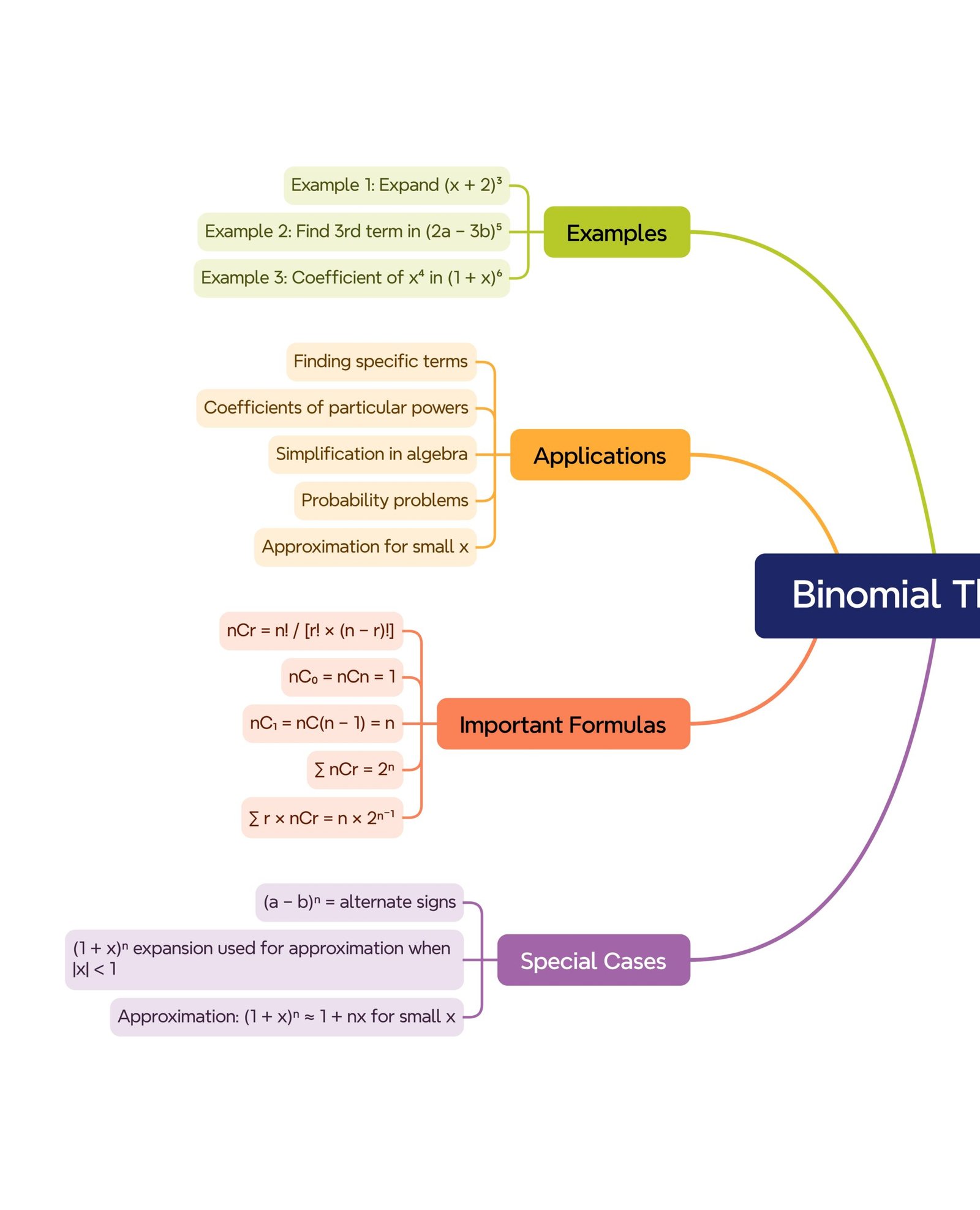
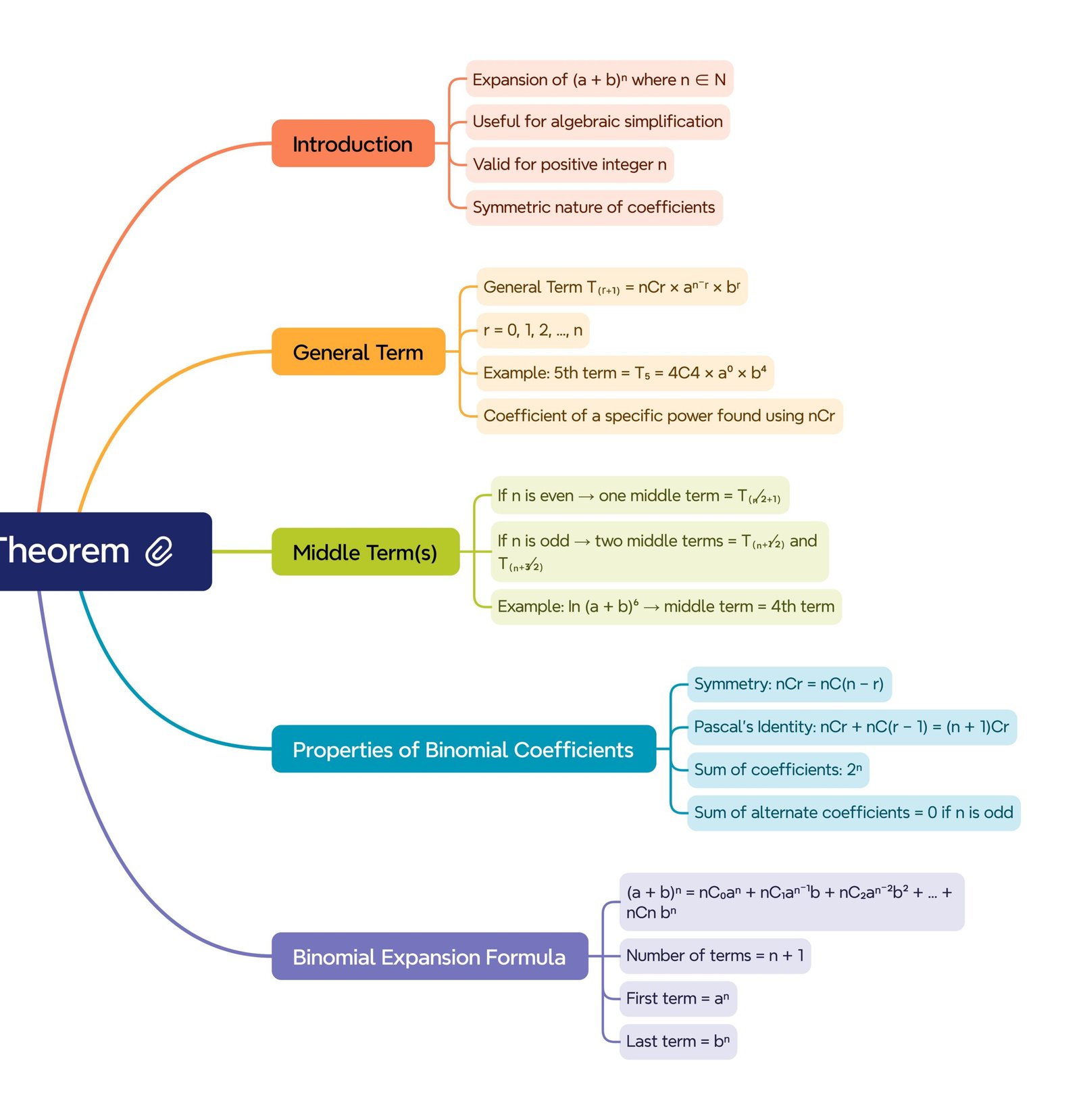
MIND MAPS
————————————————————————————————————————————————————————————————————————————
