Class 10 : Maths (In English) – Lesson 8. Introduction to Trigonometry

EXPLANATION & SUMMARY

🌟 Lesson: Introduction to Trigonometry
📖 Full Explanation

🔵 1. Setting the Stage – Why Trigonometry?
Trigonometry is the mathematics of angles and sides of triangles. Its name comes from Greek: trigonon (triangle) and metron (measure).
🟢 It is widely used in navigation, architecture, astronomy, and physics.
🟡 A right-angled triangle is the foundation: one angle = 90°, the longest side is the hypotenuse, the side opposite a chosen acute angle is called the opposite side, and the remaining is the adjacent side.
✏️ Note: “Opposite” and “adjacent” are relative to the chosen angle, not fixed labels.

🔵 2. Review of Right Triangles & Pythagoras Theorem
💡 Concept: In ΔABC (right-angled at B), the Pythagoras theorem states:
➡️ AC² = AB² + BC².
✔️ This relationship ensures every right-angled triangle obeys this fundamental property.
🟢 Example: If legs are 3 cm and 4 cm, hypotenuse = sqrt(3² + 4²) = 5 cm.

🔵 3. Defining the Primary Trigonometric Ratios
For an acute angle θ in a right triangle:
🟢 sin θ = (opposite side)/(hypotenuse)
🔵 cos θ = (adjacent side)/(hypotenuse)
🟡 tan θ = (opposite side)/(adjacent side)
The reciprocals:
🔴 cosec θ = 1/sin θ
🟢 sec θ = 1/cos θ
🔵 cot θ = 1/tan θ
✏️ Note: tan θ = sin θ / cos θ.
✔️ These definitions only hold for angles between 0° and 90° in Class 10.

🔵 4. Understanding Angle Dependence
🟢 Trigonometric ratios depend only on the angle, not on the triangle’s size.
➡️ If two right triangles have the same acute angle θ, their corresponding ratios are equal (they are similar triangles).
💡 Concept: This is why the sine of 30° is always 1/2, regardless of the triangle’s scale.

🔵 5. Deriving Standard Values – 30°, 45°, 60°
✔️ Derivation for 45°:
➤ Take an isosceles right triangle (legs = 1 unit).
➤ Hypotenuse = sqrt(2).
➤ sin 45° = 1/√2, cos 45° = 1/√2, tan 45° = 1.
✔️ Derivation for 30° & 60°:
➤ Start with an equilateral triangle of side 2 units.
➤ Split by altitude: altitude = √3.
➤ sin 30° = 1/2, cos 30° = √3/2, tan 30° = 1/√3.
➤ sin 60° = √3/2, cos 60° = 1/2, tan 60° = √3.
✏️ Note: Memorize the full table including reciprocals for θ = 0°, 30°, 45°, 60°, 90°.

🔵 6. Trigonometric Ratios of 0° and 90°
Using limits and geometry:
🟢 sin 0° = 0, cos 0° = 1, tan 0° = 0.
🔴 sin 90° = 1, cos 90° = 0, tan 90° is undefined (division by zero).
💡 Concept: Undefined values appear where denominators become zero—watch for these in simplifications.

🔵 7. Complementary Angle Relationships
🔵 Complementary angles add to 90°.
➡️ sin(90°–A) = cos A, cos(90°–A) = sin A.
➡️ tan(90°–A) = cot A, cot(90°–A) = tan A.
➡️ sec(90°–A) = cosec A, cosec(90°–A) = sec A.
🟡 Example: sin 60° = cos 30°.

🔵 8. Fundamental Trigonometric Identities
✔️ sin²A + cos²A = 1.
Divide by cos²A:
➡️ tan²A + 1 = sec²A.
Divide by sin²A:
➡️ 1 + cot²A = cosec²A.
💡 Concept: These identities are building blocks for simplification and proving results.

🔵 9. Evaluating Expressions
🟢 Example: Evaluate tan 30° + cot 60°.
➡️ tan 30° = 1/√3, cot 60° = 1/√3.
✔️ Sum = 1/√3 + 1/√3 = 2/√3.
🔴 Common Task: Use identities to simplify complex fractions or products.

🔵 10. Solving Basic Equations
🟡 Example: If cos A = √3/2, find A.
➡️ cos A = √3/2 corresponds to A = 30° (in Class 10 domain).
✏️ Note: Restrict answers to acute angles (0°–90°).

🔵 11. Geometric Proof Practice
✔️ Use similar triangles or Pythagoras theorem to prove relationships like:
➡️ tan²A = sec²A – 1.
➡️ cot²A = cosec²A – 1.

🔵 12. Real-Life Applications
🟢 Astronomy & Navigation: Determining heights of mountains or distances to inaccessible objects.
🟡 Architecture: Slopes of roofs or ramps.
🔴 Engineering: Analyzing forces and angles.
✏️ Note: While detailed height–distance problems appear in the next chapter, this chapter provides the ratio tools.

🔵 13. Linking to Other Topics
✔️ Trigonometry is foundational for:
➡️ Calculus (derivatives of sin, cos).
➡️ Physics vectors (resolving components).
➡️ Geography (map projections).

🔵 14. Common Errors and How to Avoid
🔴 Forgetting that tan 90° is undefined.
🔴 Mixing up complementary and supplementary.
🟢 Not writing the final simplified form—always rationalize denominators if required.
💡 Concept: When in doubt, draw a triangle or refer to the standard table.

🔵 15. Practice Strategy
🌿 Make a mini flashcard for the standard values.
🌿 Re-derive them occasionally to strengthen understanding.
🌿 Mix direct evaluation with simplification exercises.

📚 Summary (~300 words)
🔵 Definition & Basics
Trigonometry = study of ratios of sides of right-angled triangles.
Six ratios: sin, cos, tan, cosec, sec, cot.
Depend only on the angle, not triangle size.
🟢 Standard Values
For θ = 0°, 30°, 45°, 60°, 90°, memorize:
sin θ: 0, 1/2, 1/√2, √3/2, 1.
cos θ: 1, √3/2, 1/√2, 1/2, 0.
tan θ: 0, 1/√3, 1, √3, undefined.
Reciprocal ratios follow directly.
🟡 Complementary Angles
sin(90°–A) = cos A, cos(90°–A) = sin A.
tan(90°–A) = cot A, cot(90°–A) = tan A.
sec(90°–A) = cosec A, cosec(90°–A) = sec A.
🔴 Identities
sin²A + cos²A = 1.
1 + tan²A = sec²A.
1 + cot²A = cosec²A.
🌿 Applications
Simplifying expressions, evaluating ratios, solving equations.
Basis for heights & distances, navigation, engineering.
✏️ Tips
Always check denominators before dividing.
Use acute angles (0°–90°) only.
Redraw triangles to verify ratios.

📝 Quick Recap
🔵 Six trigonometric ratios define side relationships of a right-angled triangle.
🟢 Ratios depend only on angle magnitude, not triangle size.
🟡 Standard angles 0°, 30°, 45°, 60°, 90° with their exact values are crucial.
🔴 Complementary angle relationships link sin–cos, tan–cot, sec–cosec.
✳️ Fundamental identities: sin²A+cos²A=1, 1+tan²A=sec²A, 1+cot²A=cosec²A.
✔️ These concepts prepare you for solving real-world height/distance problems and advanced math.

———————————————————————————————————————————————————————————————————————————–

TEXT BOOK QUESTIONS

.

🌟 Exercise 8.1
🔵 Question 1
In ΔABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A (ii) sin C, cos C
🟢 Answer
💡 Concept: Use Pythagoras theorem: AC² = AB² + BC².
🔵 Step 1: AC² = 24² + 7² = 576 + 49 = 625.
🔵 Step 2: AC = sqrt(625) = 25 cm.
🔵 Step 3: sin A = BC/AC = 7/25.
🔵 Step 4: cos A = AB/AC = 24/25.
🔵 Step 5: sin C = AB/AC = 24/25.
🔵 Step 6: cos C = BC/AC = 7/25.
✔️ Final: sin A = 7/25, cos A = 24/25, sin C = 24/25, cos C = 7/25.

🔵 Question 2
In Fig 8.13, find tan P − cot R.
🟢 Answer
💡 Concept: In ΔPQR, right-angled at Q: PQ = 12 cm, QR = 5 cm (deduced), PR = 13 cm.
🔵 Step 1: Verify QR: 5² + 12² = 25 + 144 = 169 = 13². ✔️
🔵 Step 2: tan P = opposite/adjacent = QR/PQ = 5/12.
🔵 Step 3: cot R = adjacent/opposite = QR/PR? Wait, for R, adjacent = QR, opposite = PR? Correct is: cot R = adjacent/opposite = QR/PQ? For angle R, sides: opposite = PQ = 12, adjacent = QR = 5, so cot R = 5/12.
🔵 Step 4: tan P − cot R = 5/12 − 5/12 = 0.
✔️ Final: 0.

🔵 Question 3
If sin A = 3/4, calculate cos A and tan A.
🟢 Answer
🔵 Step 1: cos²A = 1 − sin²A = 1 − (9/16) = 7/16.
🔵 Step 2: cos A = sqrt(7/16) = √7/4.
🔵 Step 3: tan A = sin A / cos A = (3/4) ÷ (√7/4) = 3/√7.
✔️ Final: cos A = √7/4, tan A = 3/√7.

🔵 Question 4
Given 15 cot A = 8, find sin A and sec A.
🟢 Answer
🔵 Step 1: cot A = 8/15.
🔵 Step 2: Represent as adjacent = 8k, opposite = 15k.
🔵 Step 3: Hypotenuse = sqrt(8²k² + 15²k²) = sqrt(64 + 225) k = sqrt(289) k = 17k.
🔵 Step 4: sin A = opposite/hypotenuse = 15/17.
🔵 Step 5: cos A = adjacent/hypotenuse = 8/17 → sec A = 1/cos A = 17/8.
✔️ Final: sin A = 15/17, sec A = 17/8.

🔵 Question 5
Given sec θ = 13/12, calculate all other trigonometric ratios.
🟢 Answer
🔵 Step 1: cos θ = 1/sec θ = 12/13.
🔵 Step 2: sin²θ = 1 − cos²θ = 1 − (144/169) = 25/169.
🔵 Step 3: sin θ = 5/13.
🔵 Step 4: tan θ = sin θ/cos θ = (5/13)/(12/13) = 5/12.
🔵 Step 5: cot θ = 12/5.
🔵 Step 6: cosec θ = 1/sin θ = 13/5.
✔️ Final: sin θ = 5/13, cos θ = 12/13, tan θ = 5/12, cot θ = 12/5, cosec θ = 13/5.

🔵 Question 6
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
🟢 Answer
💡 Concept: cos x is one-to-one on (0°, 90°).
🔵 Step 1: cos A = cos B.
🔵 Step 2: Since cos is decreasing on acute angles, equality occurs only when A = B.
✔️ Final: ∠A = ∠B.

🔵 Question 7
If cot θ = 7/8, evaluate:
(i) (1 + sin θ)(1 − sin θ)/(1 + cos θ)(1 − cos θ)
(ii) cot²θ.
🟢 Answer
🔵 Step 1: Let adjacent = 7k, opposite = 8k, hypotenuse = sqrt(49 + 64)k = √113 k.
🔵 Step 2: sin θ = 8/√113, cos θ = 7/√113.
(i)
🔵 Step 3: (1 + sin θ)(1 − sin θ) = 1 − sin²θ = cos²θ.
🔵 Step 4: (1 + cos θ)(1 − cos θ) = 1 − cos²θ = sin²θ.
🔵 Step 5: Ratio = cos²θ/sin²θ = cot²θ.
🔵 Step 6: cot²θ = (7/8)² = 49/64.
✔️ Final (i): 49/64.
(ii)
✔️ Final (ii): cot²θ = 49/64.

🔵 Question 8
If 3 cot A = 4, check whether (1 − tan²A)/(1 + tan²A) = cos 2A.
🟢 Answer
🔵 Step 1: cot A = 4/3 → tan A = 3/4.
🔵 Step 2: tan²A = 9/16.
🔵 Step 3: LHS = (1 − 9/16)/(1 + 9/16) = (7/16)/(25/16) = 7/25.
🔵 Step 4: cos 2A = (1 − tan²A)/(1 + tan²A) = 7/25.
✔️ Final: Equality holds, verified.

🔵 Question 9
In ΔABC, right-angled at B, if tan A = 1/√3, find:
(i) sin A cos C + cos A sin C
(ii) cos A cos C − sin A sin C.
🟢 Answer
🔵 Step 1: tan A = 1/√3 ⇒ cot A = √3.
🔵 Step 2: Opposite = 1k, Adjacent = √3 k, Hypotenuse = 2 k.
🔵 Step 3: sin A = 1/2, cos A = √3/2.
🔵 Step 4: ∠C = 90°−A → sin C = cos A = √3/2, cos C = sin A = 1/2.
(i)
🔵 Step 5: sin A cos C + cos A sin C = (1/2)(1/2) + (√3/2)(√3/2) = 1/4 + 3/4 = 1.
(ii)
🔵 Step 6: cos A cos C − sin A sin C = (√3/2)(1/2) − (1/2)(√3/2) = √3/4 − √3/4 = 0.
✔️ Final: (i) 1 (ii) 0.

🔵 Question 10
In ΔPQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine values of sin P, cos P, and tan P.
🟢 Answer
🔵 Step 1: PR = PQ + QR? Actually PR + QR = 25. Let QR = x, then PR = 25 − x.
🔵 Step 2: Use Pythagoras: PR² = PQ² + QR².
🔵 Step 3: (25 − x)² = 25 + x².
🔵 Step 4: 625 − 50x + x² = 25 + x².
🔵 Step 5: Cancel x²: 625 − 50x = 25.
🔵 Step 6: 600 = 50x → x = 12.
🔵 Step 7: QR = 12 cm, PR = 13 cm.
🔵 Step 8: sin P = opposite/hypotenuse = QR/PR = 12/13.
🔵 Step 9: cos P = PQ/PR = 5/13.
🔵 Step 10: tan P = QR/PQ = 12/5.
✔️ Final: sin P = 12/13, cos P = 5/13, tan P = 12/5.

🔵 Question 11
State whether the following are true or false. Justify.
(i) The value of tan A is always < 1.
(ii) sec A = 12/5 for some angle A.
(iii) cos A is abbreviation of cosecant of A.
(iv) cot A is product of tan A and A.
(v) sin A = 3/4 for some angle A.
🟢 Answer
(i) 🔴 False — tan A = opposite/adjacent can be > 1 (e.g., tan 60° = √3).
(ii) 🟢 True — sec A = 12/5 occurs when cos A = 5/12, possible.
(iii) 🔴 False — cos A means cosine, not cosecant.
(iv) 🔴 False — cot A = 1/tan A, not tan A×A.
(v) 🟢 True — sin A = 3/4 possible for some acute angle.
✔️ Final: (i) False (ii) True (iii) False (iv) False (v) True.

🌟 Exercise 8.2
🔵 Question 1
Evaluate the following :
(i) sin 60° cos 30° + sin 30° cos 60°
🟢 Answer
🔵 Step 1: sin 60° = √3/2, cos 30° = √3/2, sin 30° = 1/2, cos 60° = 1/2.
🔵 Step 2: = (√3/2)(√3/2) + (1/2)(1/2) = 3/4 + 1/4.
✔️ Final: 1.

(ii) 2 tan²45° + cos²30° − sin²60°
🟢 Answer
🔵 Step 1: tan 45° = 1 ⇒ 2 tan²45° = 2.
🔵 Step 2: cos²30° = (√3/2)² = 3/4.
🔵 Step 3: sin²60° = (√3/2)² = 3/4.
🔵 Step 4: Expression = 2 + 3/4 − 3/4 = 2.
✔️ Final: 2.

(iii) (cos 45°) / (sec 30° + cosec 30°)
🟢 Answer
🔵 Step 1: cos 45° = 1/√2, sec 30° = 2/√3, cosec 30° = 2.
🔵 Step 2: Denominator = 2/√3 + 2 = 2(1/√3 + 1).
🔵 Step 3: Value = (1/√2) ÷ [2(1/√3 + 1)] = √3 / [2√2(1 + √3)].
🔵 Step 4: Rationalise (1 + √3): = √3(√3 − 1) / (4√2).
🔵 Step 5: Optional full rationalisation: = √6(√3 − 1) / 8.
✔️ Final: √6(√3 − 1)/8 (≡ √3(√3 − 1)/(4√2)).

(iv) (sin 30° + tan 45° − cosec 60°) / (sec 30° + cos 60° + cot 45°)
🟢 Answer
🔵 Step 1: Substitute → Numerator N = 1/2 + 1 − 2/√3 = 3/2 − 2/√3.
🔵 Step 2: Denominator D = 2/√3 + 1/2 + 1 = 2/√3 + 3/2.
🔵 Step 3: Multiply N and D by 2√3 → N’ = 3√3 − 4, D’ = 4 + 3√3.
🔵 Step 4: Value = (3√3 − 4)/(4 + 3√3).
🔵 Step 5: Rationalise: = [(3√3 − 4)(4 − 3√3)]/(16 − 27) = (24√3 − 43)/(−11).
✔️ Final: (43 − 24√3)/11.

(v) (5 cos²60° + 4 sec²30° − tan²45°) / (sin²30° + cos²30°)
🟢 Answer
🔵 Step 1: cos²60° = (1/2)² = 1/4 ⇒ 5 cos²60° = 5/4.
🔵 Step 2: sec²30° = (2/√3)² = 4/3 ⇒ 4 sec²30° = 16/3.
🔵 Step 3: tan²45° = 1.
🔵 Step 4: Numerator = 5/4 + 16/3 − 1 = 67/12.
🔵 Step 5: Denominator = sin²30° + cos²30° = 1/4 + 3/4 = 1.
✔️ Final: 67/12.

🔵 Question 2
Choose the correct option and justify your choice :
(i) 2 tan 30° / (1 + tan²30°) = ?
🟢 Answer
🔵 Step 1: tan 30° = 1/√3.
🔵 Step 2: Value = (2/√3)/(1 + 1/3) = (2/√3)/(4/3) = 3/(2√3) = √3/2.
✔️ Final: (A) sin 60°.

(ii) (1 − tan²45°) / (1 + tan²45°) = ?
🟢 Answer
🔵 Step 1: tan²45° = 1.
🔵 Step 2: Value = (1 − 1)/(1 + 1) = 0/2 = 0.
✔️ Final: (D) 0.

(iii) sin 2A = 2 sin A is true when A = ?
🟢 Answer
🔵 Step 1: sin 2A = 2 sin A cos A.
🔵 Step 2: 2 sin A cos A = 2 sin A ⇒ 2 sin A (cos A − 1) = 0.
🔵 Step 3: In 0°–90°, sin A = 0 or cos A = 1 ⇒ A = 0°.
✔️ Final: (A) 0°.

(iv) 2 tan 30° / (1 − tan²30°) = ?
🟢 Answer
🔵 Step 1: Use tan double-angle: tan 2A = 2 tan A / (1 − tan²A).
🔵 Step 2: Put A = 30° ⇒ tan 60° = √3.
✔️ Final: (C) tan 60°.

🔵 Question 3
If tan(A + B) = √3 and tan(A − B) = 1/√3 ; 0° < A + B ≤ 90° ; A > B, find A and B.
🟢 Answer
🔵 Step 1: tan(A + B) = √3 ⇒ A + B = 60°.
🔵 Step 2: tan(A − B) = 1/√3 ⇒ A − B = 30°.
🔵 Step 3: A = [(A + B) + (A − B)]/2 = (60° + 30°)/2 = 45°.
🔵 Step 4: B = [(A + B) − (A − B)]/2 = (60° − 30°)/2 = 15°.
✔️ Final: A = 45°, B = 15°.

🔵 Question 4
State whether the following are true or false. Justify your answer.
(i) sin(A + B) = sin A + sin B
🟢 Answer
🔵 Step 1: Identity: sin(A + B) = sin A cos B + cos A sin B.
✔️ Final: False.
(ii) The value of sin θ increases as θ increases.
🟢 Answer
🔵 Step 1: On 0°–90°, sin θ is increasing.
✔️ Final: True.
(iii) The value of cos θ increases as θ increases.
🟢 Answer
🔵 Step 1: On 0°–90°, cos θ decreases.
✔️ Final: False.
(iv) sin θ = cos θ for all values of θ.
🟢 Answer
🔵 Step 1: sin θ = cos θ ⇒ tan θ = 1 ⇒ θ = 45° (in 0°–90°).
✔️ Final: False.
(v) cot A is not defined for A = 0°.
🟢 Answer
🔵 Step 1: cot A = cos A / sin A and sin 0° = 0.
✔️ Final: True.
.

🌟 Exercise 8.3

🔵 Question 1
Express the trigonometric ratios sin A, sec A and tan A in terms of cos A.
🟢 Answer
🔵 Step 1: Use identity sin²A + cos²A = 1.
🔵 Step 2: sin²A = 1 − cos²A.
🔵 Step 3: sin A = √(1 − cos²A).
🔵 Step 4: sec A = 1/cos A.
🔵 Step 5: tan A = sin A/cos A = √(1 − cos²A)/cos A.
✔️ Final: sin A = √(1 − cos²A), sec A = 1/cos A, tan A = √(1 − cos²A)/cos A.

🔵 Question 2
Write all the other trigonometric ratios of ∠A in terms of sec A.
🟢 Answer
🔵 Step 1: sec A = 1/cos A ⇒ cos A = 1/sec A.
🔵 Step 2: sin²A = 1 − cos²A = 1 − 1/sec²A = (sec²A − 1)/sec²A.
🔵 Step 3: sin A = √(sec²A − 1)/sec A.
🔵 Step 4: tan A = sin A/cos A = (√(sec²A − 1)/sec A)/(1/sec A) = √(sec²A − 1).
🔵 Step 5: cot A = 1/tan A = 1/√(sec²A − 1).
🔵 Step 6: cosec A = 1/sin A = sec A/√(sec²A − 1).
✔️ Final: cos A = 1/sec A, sin A = √(sec²A − 1)/sec A, tan A = √(sec²A − 1), cot A = 1/√(sec²A − 1), cosec A = sec A/√(sec²A − 1).

🔵 Question 3
Choose the correct option. Justify your choice.
(i) 9 sec²A − 9 tan²A = ? (A) 1 (B) 9 (C) 8 (D) 0
🟢 Answer
🔵 Step 1: Factor 9 → 9(sec²A − tan²A).
🔵 Step 2: Use identity sec²A − tan²A = 1.
🔵 Step 3: Value = 9 × 1.
✔️ Final: 9 → Option (B).

(ii) (1 + tan θ + sec θ)(1 + cot θ − cosec θ) = ? (A) 0 (B) 1 (C) 2 (D) −1
🟢 Answer
🔵 Step 1: Put tan θ = sin θ/cos θ, sec θ = 1/cos θ, cot θ = cos θ/sin θ, cosec θ = 1/sin θ.
🔵 Step 2: First factor = (1 + sin θ/cos θ + 1/cos θ) = (cos θ + sin θ + 1)/cos θ.
🔵 Step 3: Second factor = (1 + cos θ/sin θ − 1/sin θ) = (sin θ + cos θ − 1)/sin θ.
🔵 Step 4: Product = [(cos θ + sin θ + 1)(sin θ + cos θ − 1)]/(cos θ·sin θ).
🔵 Step 5: Expand numerator: (sin θ + cos θ)² − 1.
🔵 Step 6: = (sin²θ + cos²θ + 2 sin θ cos θ) − 1 = (1 + 2 sin θ cos θ) − 1 = 2 sin θ cos θ.
🔵 Step 7: Value = [2 sin θ cos θ]/(sin θ cos θ) = 2.
✔️ Final: 2 → Option (C).

(iii) (sec A + tan A)(1 − sin A) = ? (A) sec A (B) sin A (C) cosec A (D) cos A
🟢 Answer
🔵 Step 1: Write sec A + tan A = (1 + sin A)/cos A.
🔵 Step 2: Multiply by (1 − sin A): [(1 + sin A)/cos A]·(1 − sin A).
🔵 Step 3: = (1 − sin²A)/cos A.
🔵 Step 4: = cos²A/cos A.
🔵 Step 5: = cos A.
✔️ Final: cos A → Option (D).

(iv) (1 + tan²A)/(1 + cot²A) = ? (A) sec²A (B) −1 (C) cot²A (D) tan²A
🟢 Answer
🔵 Step 1: 1 + tan²A = sec²A, 1 + cot²A = cosec²A.
🔵 Step 2: Ratio = sec²A/cosec²A.
🔵 Step 3: = (1/cos²A)/(1/sin²A) = sin²A/cos²A.
🔵 Step 4: = tan²A.
✔️ Final: tan²A → Option (D).

🔵 Question 4
Prove the following identities, where the angles involved are acute and all expressions are defined.
(i) (cosec θ − cot θ)² = (1 − cos θ)/(1 + cos θ)
🟢 Proof
🔵 Step 1: LHS = (1/sin θ − cos θ/sin θ)².
🔵 Step 2: = [(1 − cos θ)/sin θ]².
🔵 Step 3: = (1 − cos θ)²/sin²θ.
🔵 Step 4: Replace sin²θ by (1 − cos²θ).
🔵 Step 5: LHS = (1 − cos θ)²/[(1 − cos θ)(1 + cos θ)].
🔵 Step 6: Cancel (1 − cos θ).
✔️ RHS: (1 − cos θ)/(1 + cos θ). Hence proved.

(ii) cos A/(1 − sin A) + (1 + sin A)/cos A = 2 sec A
🟢 Proof
🔵 Step 1: LHS = [cos²A + (1 + sin A)(1 − sin A)]/[cos A(1 − sin A)].
🔵 Step 2: = [cos²A + (1 − sin²A)]/[cos A(1 − sin A)].
🔵 Step 3: = [cos²A + cos²A]/[cos A(1 − sin A)] = 2 cos A/(1 − sin A).
🔵 Step 4: Multiply numerator and denominator by (1 + sin A).
🔵 Step 5: = [2 cos A(1 + sin A)]/[1 − sin²A] = [2 cos A(1 + sin A)]/cos²A.
🔵 Step 6: = 2(1 + sin A)/cos A = 2 sec A.
✔️ Proved.

(iii) tan θ/(1 − cot θ) + cot θ/(1 − tan θ) = 1 + sec θ·cosec θ
🟢 Proof
🔵 Step 1: Express in sin, cos → tan θ = S/C, cot θ = C/S (write S = sin θ, C = cos θ).
🔵 Step 2: First term = (S/C)/(1 − C/S) = S²/[C(S − C)].
🔵 Step 3: Second term = (C/S)/(1 − S/C) = C²/[S(C − S)] = −C²/[S(S − C)].
🔵 Step 4: Sum = [S²/(C(S − C))] − [C²/(S(S − C))].
🔵 Step 5: = [S³ − C³]/[SC(S − C)].
🔵 Step 6: Factor numerator → (S − C)(S² + SC + C²).
🔵 Step 7: Cancel (S − C) (domain excludes S = C unless handled separately).
🔵 Step 8: = (S² + SC + C²)/(SC) = (S/C + C/S + 1).
🔵 Step 9: = tan θ + cot θ + 1 = (S² + C²)/(SC) + 1 = 1/(SC) + 1.
🔵 Step 10: = 1 + (1/C)(1/S) = 1 + sec θ·cosec θ.
✔️ Proved.

(iv) (1 + sec A)/(1 − sec A) = (1 + cos A)/(1 − cos A) (simplify each side separately)
🟢 Proof
🔵 Step 1: LHS = (1 + 1/ cos A)/(1 − 1/ cos A).
🔵 Step 2: = [(cos A + 1)/cos A]/[(cos A − 1)/cos A].
🔵 Step 3: = (cos A + 1)/(cos A − 1).
🔵 Step 4: RHS = (1 + cos A)/(1 − cos A) = (cos A + 1)/(1 − cos A).
🔵 Step 5: Multiply numerator and denominator of Step 3 by (−1).
🔵 Step 6: (cos A + 1)/(cos A − 1) = (1 + cos A)/(1 − cos A).
✔️ LHS = RHS. Proved.

(v) (cos A − sin A + 1)/(cos A + sin A − 1) = cosec A + cot A
🟢 Proof
🔵 Step 1: Multiply numerator and denominator by (cos A + sin A + 1).
🔵 Step 2: Numerator = (cos A − sin A + 1)(cos A + sin A + 1).
🔵 Step 3: = (cos A + 1)² − (sin A)².
🔵 Step 4: = (cos²A + 2 cos A + 1) − sin²A = (cos²A − sin²A) + 2 cos A + 1.
🔵 Step 5: Use cos²A − sin²A = cos 2A (not needed next); instead, use sin²A = 1 − cos²A:
🔵 Step 6: Numerator = cos²A − (1 − cos²A) + 2 cos A + 1 = 2 cos²A + 2 cos A.
🔵 Step 7: = 2 cos A(1 + cos A).
🔵 Step 8: Denominator = (cos A + sin A − 1)(cos A + sin A + 1) = (cos A + sin A)² − 1.
🔵 Step 9: = (cos²A + sin²A + 2 sin A cos A) − 1 = 2 sin A cos A.
🔵 Step 10: Fraction = [2 cos A(1 + cos A)]/[2 sin A cos A] = (1 + cos A)/sin A.
🔵 Step 11: (1 + cos A)/sin A = 1/sin A + cos A/sin A = cosec A + cot A.
✔️ Proved.

(vi) √((1 + sin A)/(1 − sin A)) = sec A + tan A
🟢 Proof
🔵 Step 1: Multiply inside radical by (1 + sin A)/(1 + sin A).
🔵 Step 2: √( (1 + sin A)² / (1 − sin²A) ).
🔵 Step 3: = √( (1 + sin A)² / cos²A ).
🔵 Step 4: = (1 + sin A)/cos A (cos A > 0 for acute A).
🔵 Step 5: = sec A + tan A.
✔️ Proved.

(vii) (sin θ − 2 sin³θ)/(2 cos³θ − cos θ) = tan θ
🟢 Proof
🔵 Step 1: Numerator = sin θ(1 − 2 sin²θ).
🔵 Step 2: = sin θ[1 − 2(1 − cos²θ)] = sin θ(2 cos²θ − 1).
🔵 Step 3: Denominator = cos θ(2 cos²θ − 1).
🔵 Step 4: Ratio = [sin θ(2 cos²θ − 1)]/[cos θ(2 cos²θ − 1)].
🔵 Step 5: Cancel (2 cos²θ − 1) (non-zero in domain).
🔵 Step 6: = sin θ/cos θ = tan θ.
✔️ Proved.

(viii) (sin A + cosec A)² + (cos A + sec A)² = 7 + tan²A + cot²A
🟢 Proof
🔵 Step 1: Expand first square → sin²A + 2 sin A·cosec A + cosec²A.
🔵 Step 2: = sin²A + 2 + cosec²A.
🔵 Step 3: Expand second square → cos²A + 2 cos A·sec A + sec²A.
🔵 Step 4: = cos²A + 2 + sec²A.
🔵 Step 5: Sum = (sin²A + cos²A) + 4 + (cosec²A + sec²A).
🔵 Step 6: = 1 + 4 + (1 + cot²A) + (1 + tan²A).
🔵 Step 7: = 7 + tan²A + cot²A.
✔️ Proved.

(ix) (cosec A − sin A)(sec A − cos A) = 1/(tan A + cot A)
🟢 Proof
🔵 Step 1: LHS = (1/sin A − sin A)(1/cos A − cos A).
🔵 Step 2: = [(1 − sin²A)/sin A]·[(1 − cos²A)/cos A].
🔵 Step 3: = [cos²A/sin A]·[sin²A/cos A].
🔵 Step 4: = (sin A cos A).
🔵 Step 5: RHS = 1/(tan A + cot A) = 1/(sin A/cos A + cos A/sin A).
🔵 Step 6: = 1/[(sin²A + cos²A)/(sin A cos A)] = (sin A cos A).
✔️ LHS = RHS. Proved.

(x) ((1 + tan²A)/(1 + cot²A)) · ((1 − tan A)/(1 − cot A))² = ?
🟢 Evaluation (step-by-step)
🔵 Step 1: Use identities 1 + tan²A = sec²A, 1 + cot²A = cosec²A.
🔵 Step 2: First factor = sec²A/cosec²A = (1/cos²A)/(1/sin²A) = sin²A/cos²A = tan²A.
🔵 Step 3: Second factor = ((1 − tan A)/(1 − cot A))².
🔵 Step 4: Put tan A = sin A/cos A, cot A = cos A/sin A.
🔵 Step 5: (1 − tan A)/(1 − cot A) = (1 − sin A/cos A)/(1 − cos A/sin A).
🔵 Step 6: = ((cos A − sin A)/cos A)/((sin A − cos A)/sin A).
🔵 Step 7: = [(cos A − sin A)/cos A]·[sin A/(sin A − cos A)].
🔵 Step 8: = [sin A(cos A − sin A)]/[cos A(−(cos A − sin A))] = −(sin A/cos A) = −tan A.
🔵 Step 9: Square → ((1 − tan A)/(1 − cot A))² = (tan A)².
🔵 Step 10: Product = tan²A × tan²A = tan⁴A.
✔️ Final: The LHS simplifies to tan⁴A.

————————————————————————————————————————————————————————————————————————————

OTHER IMPORTANT QUESTIONS FOR EXAMS

BOARD STYLE MODEL PAPER

(Total: 30 questions, 80 marks; Sections A–D; )

🌟 SECTION A — Multiple Choice Questions (1 mark each)
🔵 Question 1:
The value of sin 30° is:
🟢 (A) 1
🔴 (B) 1/√3
🟡 (C) 1/2
🔵 (D) √3/2
Answer: ✔️ (C) 1/2

🔵 Question 2:
If tan A = 1, then A equals:
🟢 (A) 30°
🔴 (B) 45°
🟡 (C) 60°
🔵 (D) 90°
Answer: ✔️ (B) 45°

🔵 Question 3:
cos 60° = ?
🟢 (A) 0
🔴 (B) 1/2
🟡 (C) √3/2
🔵 (D) 1
Answer: ✔️ (B) 1/2

🔵 Question 4:
Which of the following is not defined?
🟢 (A) tan 90°
🔴 (B) sin 0°
🟡 (C) cos 90°
🔵 (D) tan 45°
Answer: ✔️ (A) tan 90°

🔵 Question 5:
If sin θ = 3/5, then cos θ = ? (θ acute)
🟢 (A) 4/5
🔴 (B) √(1−9/25)
🟡 (C) 2/5
🔵 (D) 5/3
Answer: ✔️ (A) 4/5

🔵 Question 6:
The value of cot 30° is:
🟢 (A) √3
🔴 (B) 1/√3
🟡 (C) 2
🔵 (D) 1/2
Answer: ✔️ (A) √3

🔵 Question 7:
sec²A − tan²A = ?
🟢 (A) 0
🔴 (B) 1
🟡 (C) 2
🔵 (D) sec A
Answer: ✔️ (B) 1

🔵 Question 8:
If cos A = 12/13, then tan A = ? (A acute)
🟢 (A) 5/12
🔴 (B) 12/5
🟡 (C) 5/13
🔵 (D) 13/5
Answer: ✔️ (A) 5/12

🔵 Question 9:
sin ²θ + cos ²θ = ?
🟢 (A) 0
🔴 (B) 1
🟡 (C) 2
🔵 (D) sec²θ
Answer: ✔️ (B) 1

🔵 Question 10:
In a right triangle, if the side opposite A is 8 and hypotenuse is 10, find sin A.
🟢 (A) 3/5
🔴 (B) 4/5
🟡 (C) 5/8
🔵 (D) 4/3
Answer: ✔️ (B) 4/5

🔵 Question 11:
The angle whose sine is √3/2 is:
🟢 (A) 30°
🔴 (B) 45°
🟡 (C) 60°
🔵 (D) 90°
Answer: ✔️ (C) 60°

🔵 Question 12:
If cot A = 3/4, find sec A. (Show steps)
🟢 Answer:
✏️ Step 1 (Relation): 1 + cot²A = csc²A
➡️ csc²A = 1 + (3/4)² = 1 + 9/16 = 25/16
✏️ Step 2: csc A = 5/4
➡️ sin A = 1/csc A = 4/5
✏️ Step 3: cos²A = 1 − sin²A = 1 − (16/25) = 9/25
➡️ cos A = 3/5 (A acute ⇒ positive)
✏️ Step 4: sec A = 1/cos A = 5/3
✔️ Final answer: sec A = 5/3

🔵 Question 13:
The value of cos²30° + sin²30° is:
🟢 (A) 1/2
🔴 (B) 1
🟡 (C) 3/2
🔵 (D) √3/2
Answer: ✔️ (B) 1

🔵 Question 14:
If sec A = 5/3, then tan A = ? (A acute)
🟢 (A) 4/3
🔴 (B) 5/4
🟡 (C) 3/4
🔵 (D) 3/5
Answer: ✔️ (A) 4/3

🔵 Question 15:
sin 0° + cos 90° equals:
🟢 (A) 0
🔴 (B) 1
🟡 (C) 2
🔵 (D) √3/2
Answer: ✔️ (A) 0

🔵 Question 16:
If tan θ = √3, find θ.
🟢 (A) 30°
🔴 (B) 45°
🟡 (C) 60°
🔵 (D) 90°
Answer: ✔️ (C) 60°

🔵 Question 17:
Find the value of cot 45°.
🟢 (A) 1
🔴 (B) 0
🟡 (C) √3
🔵 (D) 1/√3
Answer: ✔️ (A) 1

🔵 Question 18:
The complement of 65° is:
🟢 (A) 25°
🔴 (B) 35°
🟡 (C) 45°
🔵 (D) 55°
Answer: ✔️ (A) 25°

🌟 SECTION B — Very Short Answer (2 marks each)
🔵 Question 19:
If sin A = 12/13, find cos A and tan A.
🟢 Answer:
✏️ Step 1: cos²A = 1 − sin²A = 1 − (144/169) = 25/169
➡️ cos A = 5/13
✏️ Step 2: tan A = sin A / cos A = (12/13) ÷ (5/13) = 12/5
✔️ Final: cos A = 5/13, tan A = 12/5

🔵 Question 20:
Prove: 1 + tan²A = sec²A
🟢 Answer:
✏️ Step 1: Start with RHS identity of Pythagoras: sin²A + cos²A = 1
✏️ Step 2: Divide both sides by cos²A:
➡️ (sin²A / cos²A) + 1 = 1 / cos²A
➡️ tan²A + 1 = sec²A
✔️ Final: Proved

🔵 Question 21:
A tower’s shadow is √3 times its height when the Sun’s altitude is θ. Find θ.
🟢 Answer:
✏️ Step 1: tan θ = (height)/(shadow) = h/(√3 h) = 1/√3
✏️ Step 2: tan 30° = 1/√3
✔️ Final: θ = 30°

🔵 Question 22:
Find the value of: sin 60° · cos 30° + cos 60° · sin 30°
🟢 Answer:
✏️ Step 1: Recognize formula: sin A cos B + cos A sin B = sin(A + B)
✏️ Step 2: Substitute A=60°, B=30°:
➡️ = sin(60° + 30°) = sin 90°
✏️ Step 3: sin 90° = 1
✔️ Final: 1

🔵 Question 23:
Prove: csc²A − cot²A = 1
🟢 Answer:
✏️ Step 1: Start from Pythagorean identity: 1 + cot²A = csc²A
➡️ Rearrange: csc²A − cot²A = 1
✔️ Final: Proved

🌟 SECTION C — Short Answer-II (3 marks each)
🔵 Question 24:
A ladder 10 m long leans against a vertical wall making an angle of 60° with the horizontal. Find the height up the wall the ladder reaches.
🟢 Answer:
✏️ Step 1: sin 60° = h / 10
➡️ √3/2 = h / 10
✏️ Step 2: h = 10 × √3 / 2 = 5√3 m
✔️ Final: Height = 5√3 m

🔵 Question 25:
Find the value of (2 tan 30°) / (1 − tan² 30°).
🟢 Answer:
✏️ Step 1: tan 30° = 1/√3
➡️ Substitute: (2 × 1/√3) / (1 − 1/3)
✏️ Step 2: = (2/√3) / (2/3)
✏️ Step 3: = (2/√3) × (3/2) = 3/√3 = √3
✔️ Final: √3

🔵 Question 26:
Find the value of sin 48° cos 42° + cos 48° sin 42°.
🟢 Answer:
✏️ Step 1: Use identity: sin A cos B + cos A sin B = sin(A + B)
➡️ = sin(48° + 42°)
✏️ Step 2: = sin 90° = 1
✔️ Final: 1

🔵 Question 27:
A man observes the top of a building at an angle of elevation of 30°. After walking 20 m towards the building, the angle becomes 60°. Find the building’s height.
🟢 Answer:
✏️ Let initial distance = x, height = h.
✏️ tan 30° = h / x ⇒ h = x / √3
✏️ tan 60° = h / (x − 20) ⇒ √3 = h / (x − 20) ⇒ h = √3 (x − 20)
➡️ x / √3 = √3 (x − 20)
✏️ Multiply by √3: x = 3(x − 20)
✏️ x = 3x − 60 ⇒ −2x = −60 ⇒ x = 30 m
✏️ h = x / √3 = 30 / √3 = 10√3 m
✔️ Final: Building height = 10√3 m

🌟 SECTION D — Long Answer (4 marks each)
🔵 Question 28:
Prove: (1 − cot A) / (1 + cot A) = (tan A − 1) / (tan A + 1)
🟢 Answer:
✏️ Step 1: Rewrite cot A = 1 / tan A.
➡️ LHS = (1 − 1/tan A) / (1 + 1/tan A)
✏️ Step 2: Multiply numerator and denominator by tan A:
➡️ = (tan A − 1) / (tan A + 1)
✔️ Final: Proved

🔵 Question 29:
A 15 m high tower casts a shadow of length 5√3 m. Find the Sun’s altitude.
🟢 Answer:
✏️ tan θ = 15 / (5√3) = 3 / √3 = √3
➡️ θ = 60°
✔️ Final: Sun’s altitude = 60°

🔵 Question 30:
From the top of a 20 m tower, the angle of depression of a point on the ground is 45°. Find the distance of the point from the base of the tower.
🟢 Answer:
✏️ tan 45° = 20 / d ⇒ 1 = 20 / d
➡️ d = 20 m
✔️ Final: Distance from tower’s base = 20 m

———————————————————————————————————————————————————————————————————————————–

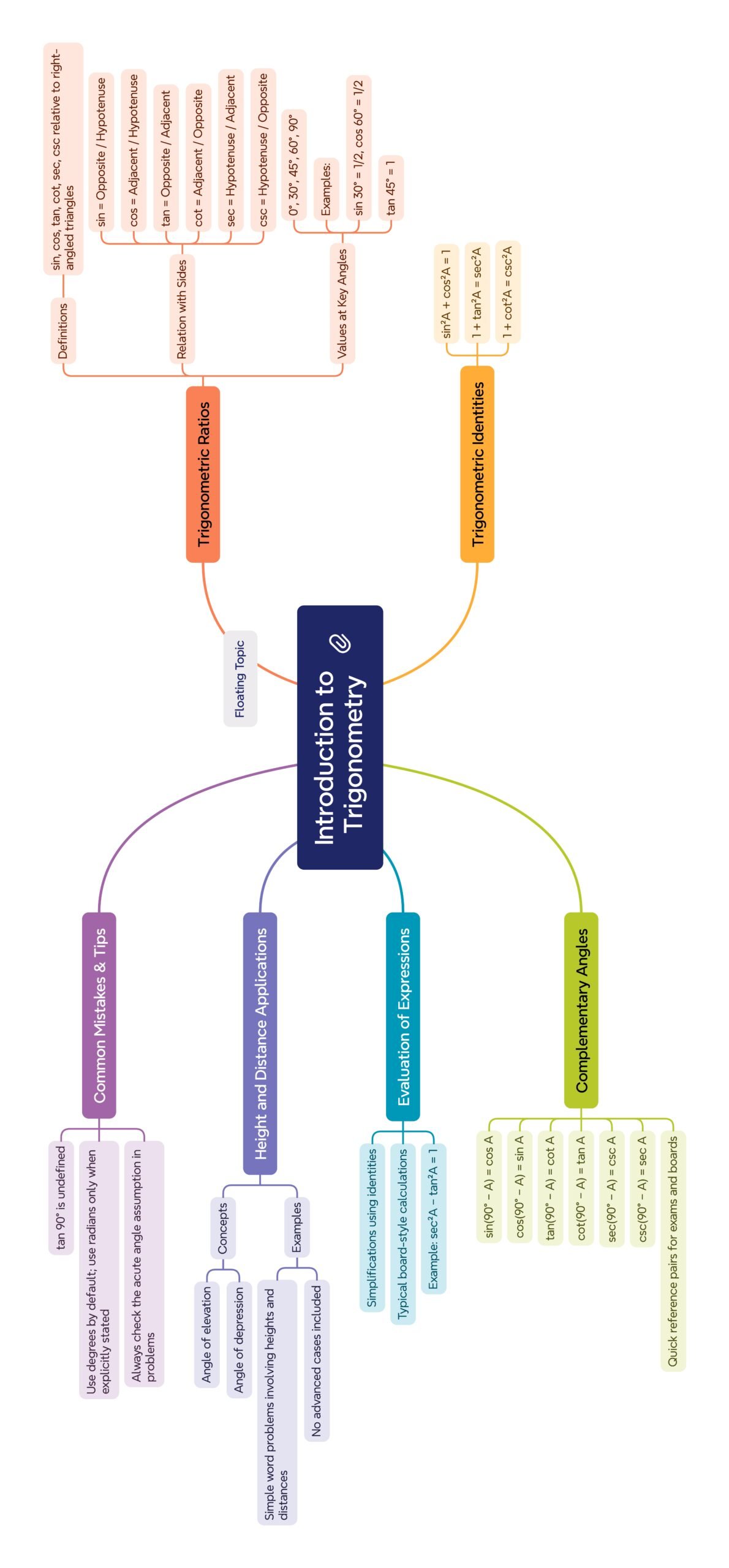
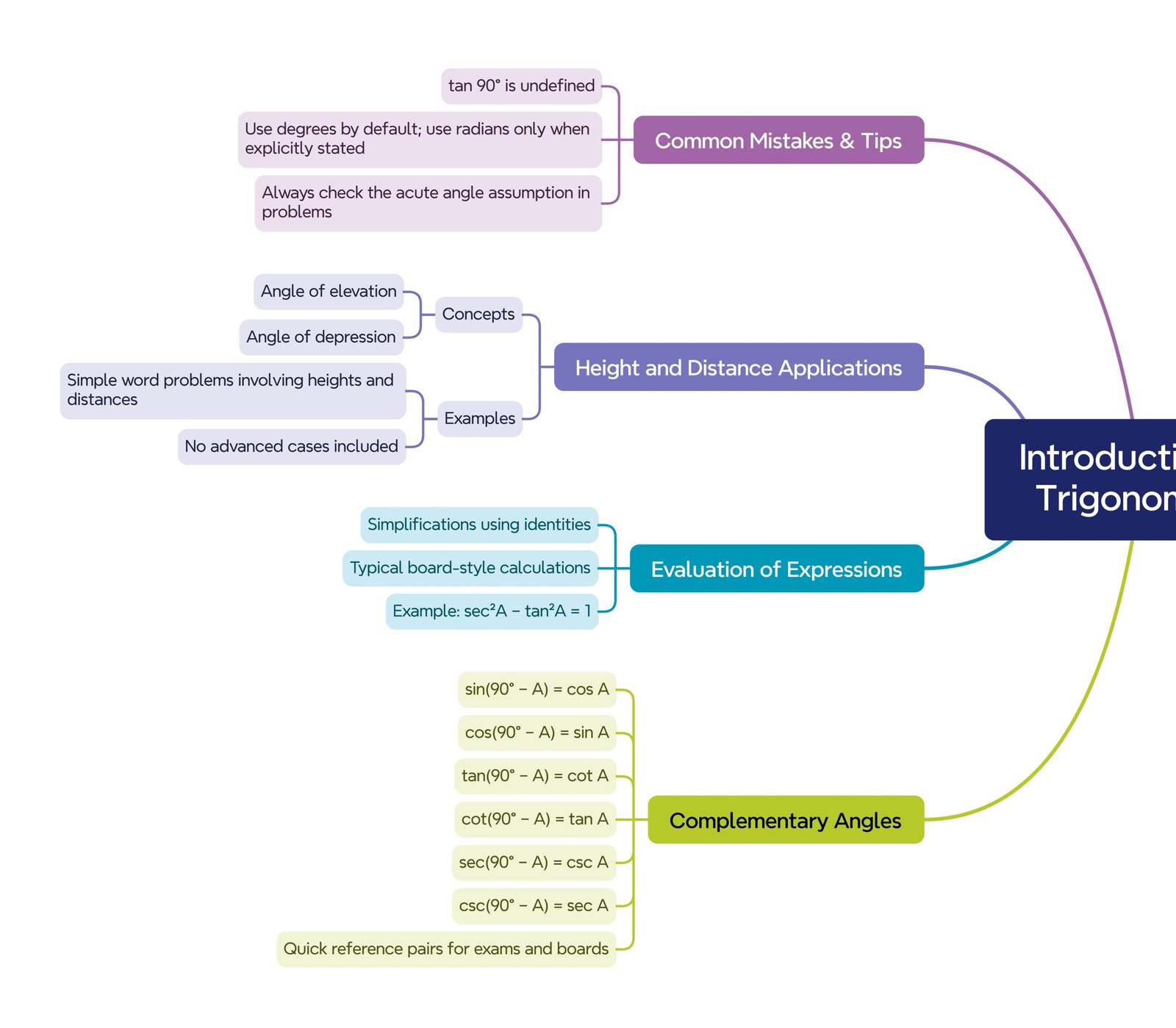
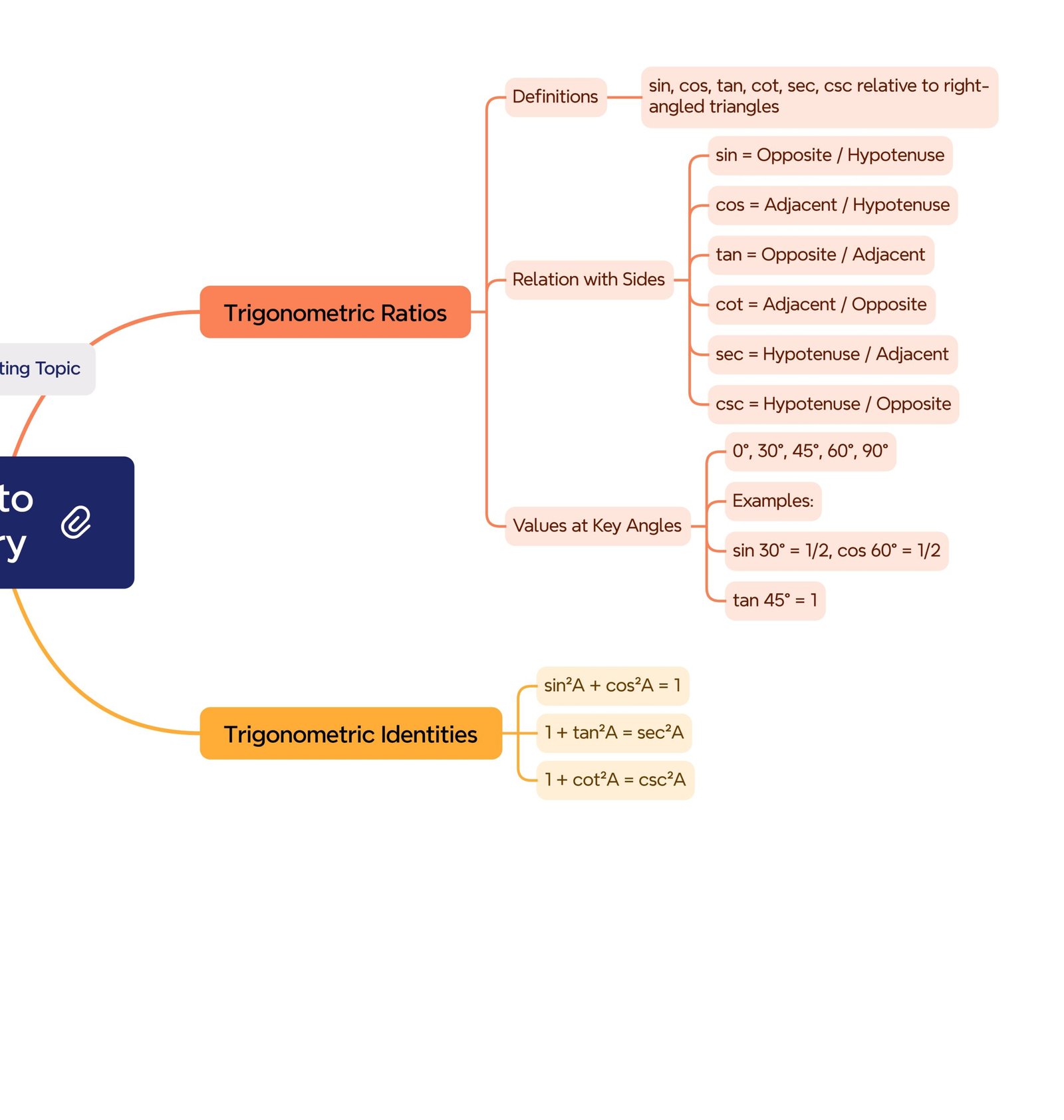
MIND MAP