Class : 9 – Science (English) : Lesson 10. Work and Energy

EXPLANATION & SUMMARY

🔵 Introduction
Every activity in daily life — walking, pushing, lifting, cycling — involves work and energy.
Work is done when a force is applied and displacement occurs.
Energy is the capacity to do work. Both concepts are closely linked.

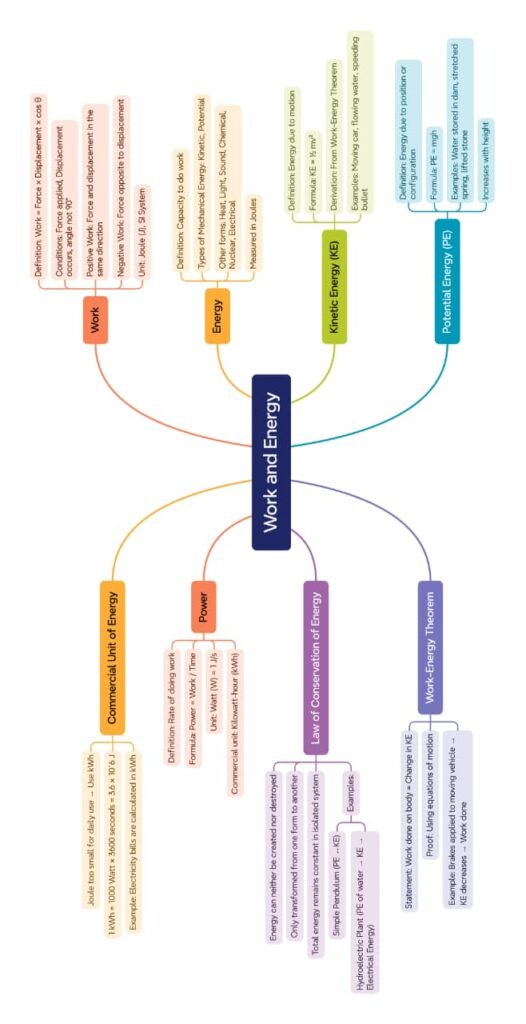
🟢 Work
Definition
Work is said to be done when:
A force is applied on a body.
The body undergoes displacement.
The displacement has a component in the direction of force.
Formula:
Work (W) = Force (F) × Displacement (d) × cos θ
θ = angle between force and displacement.
SI unit: Joule (J).
Cases
If θ = 0° (force and displacement same direction) → maximum work.
If θ = 90° → work = 0 (e.g., force on object moving in circular path).
Negative work → force opposite displacement (e.g., friction).
💡 Example: Work done in pushing a cart, lifting an object, etc.

🟡 Energy
Capacity to do work.
SI unit: Joule (same as work).
Forms: kinetic energy, potential energy, heat, light, etc.

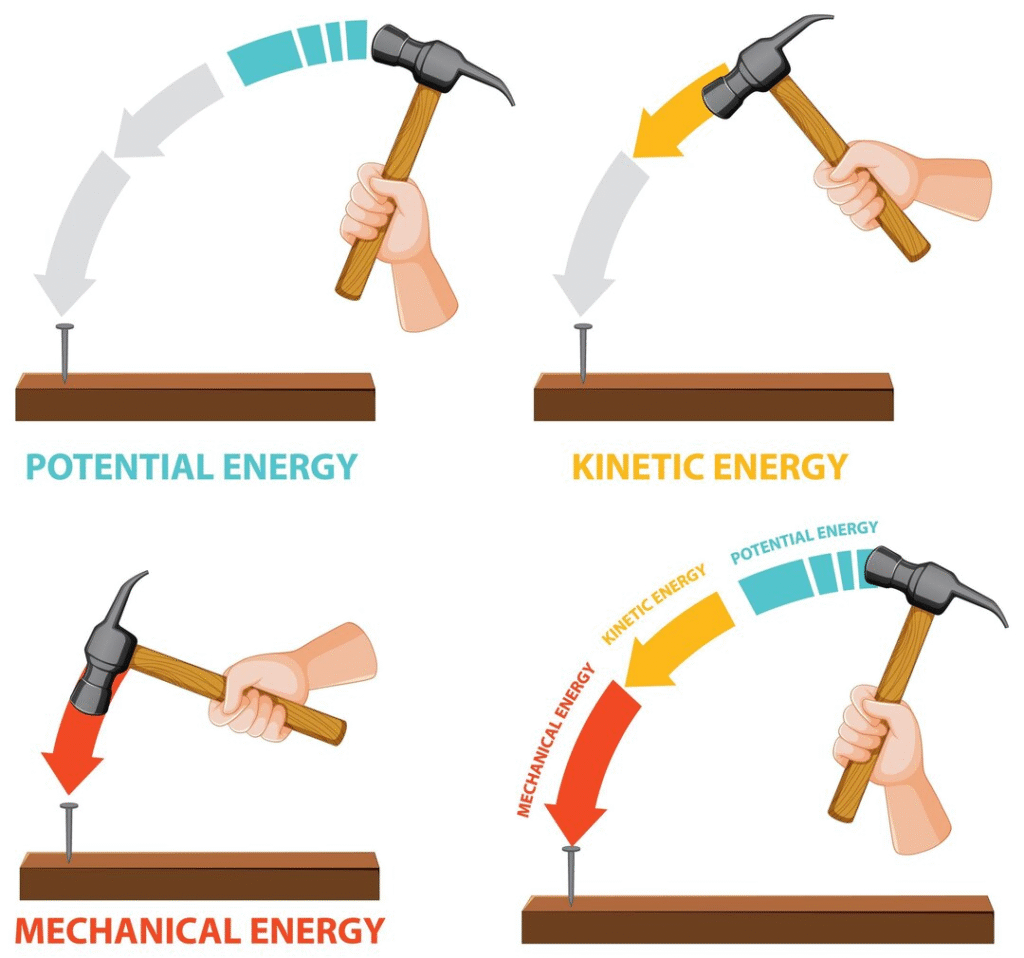
🟣 Kinetic Energy (KE)
Energy possessed by a body due to its motion.
Formula: KE = ½ m v²
Derivation:
Work done in accelerating body from rest to velocity v is W = F × d.
Using Newton’s 2nd law and equations of motion, W = ½ m v².
So work done on body = KE gained.
💡 Example: Moving car, flowing river, flying bullet.

🔴 Potential Energy (PE)
Energy possessed due to position or configuration.
Formula: PE = m g h (for height h).
Derivation:
Work done in raising body against gravity = m g h.
Stored as potential energy.
💡 Example: Water stored in dam, stretched spring, lifted stone.

🟤 Work–Energy Theorem
The work done on an object is equal to the change in its kinetic energy.
W = KE_final − KE_initial
Shows direct link between force applied and energy gained/lost.

🟠 Power
Rate of doing work.
Formula: Power (P) = Work / Time
Unit: Watt (W).
1 Watt = 1 Joule of work done in 1 second.
💡 Example: A machine doing 1000 J work in 2 s has P = 500 W.

🟣 Commercial Unit of Energy
Electrical energy measured in kilowatt-hour (kWh).
1 kWh = 1000 watt × 3600 s = 3.6 × 10^6 J.
Used in electricity bills.

🟢 Conservation of Energy
Energy can neither be created nor destroyed; only transformed.
Total energy of an isolated system remains constant.
Example: In pendulum, energy continuously changes between KE and PE, but total remains same.

🟡 Real-Life Applications
Hydroelectric power plants: PE of water → KE → electrical energy.
Vehicles: Chemical energy of fuel → KE, heat, sound.
Human body: Chemical energy in food → muscular work.

🟣 Summary
Work = F d cos θ, done when force causes displacement.
Energy = capacity to do work.
KE = ½ m v²; PE = m g h.
Work–energy theorem links work and energy.
Power = work/time; commercial unit = kWh.
Energy is conserved; only changes form.

📝 Quick Recap
🔵 Work = Force × Displacement × cos θ.
🟢 KE = ½ m v² (motion energy).
🟡 PE = m g h (position energy).
🔴 Work–Energy Theorem: Work = ΔKE.
🟤 Power = Work/Time.
🟠 1 kWh = 3.6 × 10^6 J.
🌍 Law of conservation of energy always holds.

————————————————————————————————————————————————————————————————————————————

QUESTIONS FROM TEXTBOOK

Question 1
Look at the activities listed below. Reason out whether or not work is done in the light of your understanding of the term ‘work’.
Suma is swimming in a pond.
A donkey is carrying a load on its back.
A wind-mill is lifting water from a well.
A green plant is carrying out photosynthesis.
An engine is pulling a train.
Food grains are getting dried in the sun.
A sailboat is moving due to wind energy.
Answer
🔵 Swimming: Work is done (muscular force causes displacement of water and the swimmer).
🟢 Donkey carrying load on level road: No work on the load (force by donkey on load is mainly vertical; displacement is horizontal → angle 90° → work zero).
🟡 Wind-mill lifting water: Work is done (force and displacement are along lift).
🟣 Photosynthesis: No mechanical work (chemical process, no force–displacement pair).
🔴 Engine pulling a train: Work is done (tractive force causes displacement).
🟤 Drying grains in the sun: No mechanical work (heating/evaporation, not force×displacement).
🟠 Sailboat moving due to wind: Work is done (wind force causes displacement).

Question 2
An object thrown at a certain angle to the ground moves in a curved path and falls back to the ground. The initial and final points lie on the same horizontal line. What is the work done by the force of gravity on the object?
Answer
Idea: Work by gravity depends on vertical displacement only.
Start height = end height → net vertical displacement = 0.
Therefore work by gravity over the whole flight = 0 J.

Question 3
A battery lights a bulb. Describe the energy changes involved in the process.
Answer
🔋 Chemical energy (battery) → ⚡ Electrical energy (in circuit) → 💡 Light energy + 🔥 Heat energy (in filament/LED).

Question 4
Certain force acting on a 20 kg mass changes its velocity from 5 m/s to 2 m/s. Calculate the work done by the force.
Answer
Given: m = 20 kg, u = 5 m/s, v = 2 m/s
To find: Work W
Formula: W = change in kinetic energy = (1/2) m (v^2 − u^2)
Steps:
v^2 = 2^2 = 4
u^2 = 5^2 = 25
v^2 − u^2 = 4 − 25 = −21
(1/2) m (v^2 − u^2) = 0.5 × 20 × (−21) = −210
Final: W = −210 J (negative → force removed kinetic energy).

Question 5
A mass of 10 kg is at point A on a table. It is moved to point B. If the line joining A and B is horizontal, what is the work done on the object by the gravitational force? Explain.
Answer
Weight acts vertically downward; displacement is horizontal.
Angle between force and displacement = 90°.
Work = F d cos(90°) = 0 → Work by gravity = 0 J.

Question 6
The potential energy of a freely falling object decreases progressively. Does this violate the law of conservation of energy? Why?
Answer
No. As the object falls, potential energy converts to kinetic energy.
Total mechanical energy (PE + KE) remains approximately constant (ignoring air resistance).

Question 7
What are the various energy transformations that occur when you are riding a bicycle?
Answer
🍎 Chemical energy in muscles → 🔥 Heat (in muscles) + ⚙️ Mechanical energy.
⚙️ Mechanical energy → 🚲 Kinetic energy of bicycle + 🔊 Sound + 🔥 Heat (friction in chain, bearings, tyres).
Uphill: part of energy → 🗻 Gravitational potential energy.

Question 8
Does the transfer of energy take place when you push a huge rock with all your might and fail to move it? Where is the energy you spend going?
Answer
No work on the rock (no displacement).
Your chemical energy → internal energy/heat in your muscles; a small part as heat at the contact surfaces and sound.

Question 9
A certain household has consumed 250 units of energy during a month. How much energy is this in joules?
Answer
Given: 1 unit = 1 kWh = 3.6 × 10^6 J
Steps:
Energy = 250 × (3.6 × 10^6)
Energy = 900 × 10^6 J
Final: 9.0 × 10^8 J.

Question 10
An object of mass 40 kg is raised to a height of 5 m above the ground. What is its potential energy? If the object is allowed to fall, find its kinetic energy when it is halfway down. (Take g = 9.8 m/s^2)
Answer
Part 1 (PE at 5 m):
PE = m g h = 40 × 9.8 × 5 = 1960 J
Part 2 (KE halfway down → at 2.5 m drop):
Loss of PE = m g h/2 = 40 × 9.8 × 2.5 = 980 J
Ignoring air resistance, KE at halfway = 980 J.
Final: PE = 1960 J; KE at halfway = 980 J.

Question 11
What is the work done by the force of gravity on a satellite moving round the earth? Justify your answer.
Answer
For circular motion, at each instant gravity is radial and displacement is tangential → angle 90°.
Work = F d cos(90°) = 0 → Net work by gravity = 0 J over any part of the orbit.

Question 12
Can there be displacement of an object in the absence of any force acting on it?
Answer
Yes. If an object is already moving with constant velocity (no net force), it keeps moving and hence has displacement. (Newton’s first law; e.g., object drifting in deep space.)

Question 13
A person holds a bundle of hay over his head for 30 minutes and gets tired. Has he done some work or not? Justify.
Answer
No work on the bundle (no displacement).
Tiredness comes from internal muscular activity converting chemical energy to heat, not from mechanical work on the load.

Question 14
An electric heater is rated 1500 W. How much energy does it use in 10 hours?
Answer
Given: P = 1500 W, t = 10 h = 10 × 3600 s = 36 000 s
Steps:
Energy E = P × t = 1500 × 36 000 = 54 000 000 J
In kWh: E = (1500 W × 10 h) = 15 kWh
Final: 5.4 × 10^7 J ( = 15 kWh ).

Question 15
Illustrate the law of conservation of energy by discussing the energy changes which occur when we draw a pendulum bob to one side and allow it to oscillate. Why does the bob eventually come to rest? What happens to its energy eventually? Is it a violation of the law?
Answer
At extreme position: PE maximum, KE zero.
At mean position: KE maximum, PE minimum.
Total energy (PE + KE) ≈ constant.
The bob finally stops due to air resistance and friction at the support; mechanical energy slowly changes into heat and sound.
No violation: energy is conserved but transformed.

Question 16
An object of mass m is moving with a constant velocity v. How much work should be done on the object in order to bring the object to rest?
Answer
Initial KE = (1/2) m v^2
Final KE = 0
Work done by external agent = change in KE = 0 − (1/2) m v^2
Magnitude of work required = (1/2) m v^2 (done against the motion).

Question 17
Calculate the work required to be done to stop a car of 1500 kg moving at a velocity of 60 km/h.
Answer
Given: m = 1500 kg, v = 60 km/h = 16.67 m/s
Steps:
KE = (1/2) m v^2
v^2 = (16.67)^2 ≈ 277.8
(1/2) m v^2 = 0.5 × 1500 × 277.8 = 208 350 J (≈ 2.08 × 10^5 J)
Final: 2.08 × 10^5 J of work (magnitude) must be done to stop it.

Question 18
In each of the following a force F is acting on an object of mass m. The direction of displacement is from west to east (shown by the longer arrow). Observe the diagrams carefully and state whether the work done by the force is negative, positive or zero.
Answer
Diagram 1: Force upward (north), displacement east → angle 90° → Work = 0.
Diagram 2: Force east, displacement east → angle 0° → Work positive.
Diagram 3: Force west, displacement east → angle 180° → Work negative.

Question 19
Soni says that the acceleration of an object could be zero even when several forces are acting on it. Do you agree? Why?
Answer
✅ Agree. When forces balance so that net force = 0, acceleration is zero (object at rest or moving with constant velocity). Example: car cruising at uniform speed with engine force balanced by resistive forces.

Question 20
Find the energy in joules consumed in 10 hours by four devices of power 500 W each.
Answer
Given: Power per device = 500 W; number = 4; total power P = 2000 W
Time t = 10 h = 36 000 s
Steps:
E = P × t = 2000 × 36 000 = 72 000 000 J
In kWh: 2 kW × 10 h = 20 kWh
Final: 7.2 × 10^7 J ( = 20 kWh ).

Question 21
A freely falling object eventually stops on reaching the ground. What happens to its kinetic energy?
Answer
On impact, kinetic energy changes into heat, sound, and deformation energy of the ground/object (and partly into internal energy). Energy is not lost, only transformed.

————————————————————————————————————————————————————————————————————————————

OTHER IMPORTANT QUESTIONS FOR EXAMS

Section A – Multiple Choice Questions (Q1 – Q12, 1 mark each)
Q1. Work is said to be done when:
🔵 (a) Force is applied on a body
🟢 (b) Body is displaced
🟡 (c) Force is applied and body is displaced
🟣 (d) None of these
✅ Answer: (c)

Q2. SI unit of power is:
🔵 (a) Joule
🟢 (b) Watt
🟡 (c) Newton
🟣 (d) Erg
✅ Answer: (b)

Q3. An electric bulb of 100 W is used for 10 hours. The energy consumed is:
🔵 (a) 0.1 kWh
🟢 (b) 1 kWh
🟡 (c) 10 kWh
🟣 (d) 100 kWh
✅ Answer: (b)

Q4. A body is moved vertically upward. The work done against gravity is stored as:
🔵 (a) Heat energy
🟢 (b) Potential energy
🟡 (c) Kinetic energy
🟣 (d) Chemical energy
✅ Answer: (b)

Q5. Which of the following is not a commercial unit of energy?
🔵 (a) kWh
🟢 (b) Joule
🟡 (c) Calorie
🟣 (d) Watt
✅ Answer: (d)

Q6. Work done by centripetal force on a satellite in circular orbit is:
🔵 (a) Positive
🟢 (b) Negative
🟡 (c) Zero
🟣 (d) Infinite
✅ Answer: (c)

Q7. When a body falls freely under gravity, its:
🔵 (a) Potential energy increases
🟢 (b) Kinetic energy decreases
🟡 (c) Potential energy decreases and kinetic energy increases
🟣 (d) Both energies remain constant
✅ Answer: (c)

Q8. A machine is 75% efficient. If it gives 150 J of useful work, input energy is:
🔵 (a) 200 J
🟢 (b) 100 J
🟡 (c) 75 J
🟣 (d) 50 J
✅ Answer: (a)

Q9. 1 horse power (HP) =
🔵 (a) 736 W
🟢 (b) 1000 W
🟡 (c) 746 W
🟣 (d) 700 W
✅ Answer: (c)

Q10. Energy possessed by a moving body is:
🔵 (a) Potential energy
🟢 (b) Kinetic energy
🟡 (c) Heat energy
🟣 (d) Chemical energy
✅ Answer: (b)

Q11. The law of conservation of energy states that:
🔵 (a) Energy can be created
🟢 (b) Energy can be destroyed
🟡 (c) Energy can neither be created nor destroyed, only transformed
🟣 (d) Total energy decreases in transformations
✅ Answer: (c)

Q12. SI unit of work is:
🔵 (a) Watt
🟢 (b) Joule
🟡 (c) Newton
🟣 (d) Horse Power
✅ Answer: (b)

Section B – Very Short Answer (Q13 – Q20, 2 marks each)
Q13. Define 1 joule of work.
✅ Answer: Work done is 1 joule when a force of 1 N displaces a body by 1 m in the direction of the force.

Q14. A force of 20 N displaces a body by 5 m in the direction of force. Find the work done.
Step 1: W = F × d
Step 2: W = 20 × 5 = 100 J
✅ Answer: 100 J

Q15. What is meant by kinetic energy? Write its formula.
✅ Answer: Energy possessed by a body due to its motion.
Formula: KE = (1/2) m v²

Q16. Define power. State its SI unit.
✅ Answer: Power is the rate of doing work. SI unit: Watt (W).

Q17. When is the work done on a body said to be negative?
✅ Answer: When the applied force and displacement are in opposite directions (e.g., frictional force).

Q18. An electric motor takes 5 A current from 220 V supply. If it runs for 2 hours, calculate energy consumed in kWh.
Step 1: P = VI = 220 × 5 = 1100 W
Step 2: t = 2 h = 2 kWh
Step 3: Energy = P × t = 1.1 kW × 2 = 2.2 kWh
✅ Answer: 2.2 kWh

Q19. Write the expression for gravitational potential energy.
✅ Answer: PE = m g h

Q20. A ball of mass 0.5 kg is thrown upwards with velocity 10 m/s. Find its kinetic energy.
Step 1: KE = ½ m v²
Step 2: = ½ × 0.5 × (10)²
Step 3: = 0.25 × 100 = 25 J
✅ Answer: 25 J

Section C – Short Answer (Q21 – Q28, 3 marks each)
Q21. A body of mass 2 kg is lifted through a height of 2.5 m. Calculate work done.
Step 1: W = m g h
Step 2: = 2 × 9.8 × 2.5
Step 3: = 49 J
✅ Answer: 49 J

Q22. State the law of conservation of energy. Give one example.
✅ Answer: Energy can neither be created nor destroyed, it can only be transformed. Example: In a simple pendulum, PE ↔ KE.

Q23. A stone of mass 500 g is thrown vertically upward with a speed of 20 m/s. Find the maximum height reached. (Take g = 10 m/s²)
Step 1: At top, KE = 0, all KE → PE
Step 2: Initial KE = ½ m v² = 0.5 × 0.5 × 400 = 100 J
Step 3: PE = m g h = KE
Step 4: h = 100 / (0.5 × 10) = 20 m
✅ Answer: 20 m

Q24. Differentiate between work and power.
✅ Answer:
Work = product of force × displacement in direction of force (scalar).
Power = rate of doing work (scalar).

Q25. A 60 W bulb is used for 6 hours daily. Calculate energy consumed in 30 days.
Step 1: Energy per day = 60 × 6 = 360 Wh = 0.36 kWh
Step 2: For 30 days = 0.36 × 30 = 10.8 kWh
✅ Answer: 10.8 kWh

Q26. Write three commercial sources of energy.
✅ Answer: Coal, Petroleum, Electricity.

Q27. A hammer of mass 2 kg strikes a nail with velocity 5 m/s. If nail goes 2.5 cm deep, find average force on nail.
Step 1: KE = ½ m v² = 0.5 × 2 × 25 = 25 J
Step 2: Work = Force × distance
Step 3: Force = Work / d = 25 / 0.025 = 1000 N
✅ Answer: 1000 N

Q28. A pump raises 500 kg of water to height 50 m in 5 min. Find power of pump. (Take g = 10 m/s²)
Step 1: Work = m g h = 500 × 10 × 50 = 250 000 J
Step 2: Time = 300 s
Step 3: Power = Work / time = 250 000 / 300 ≈ 833.3 W
✅ Answer: 833 W

Section D – Long Answer (Q29 – Q35, 5 marks each)
Q29. Derive an expression for kinetic energy of a body moving with velocity v.
✅ Answer: (Derivation explained step by step with equations of motion – KE = ½ m v²).

Q30. A boy of 40 kg runs upstairs to height 10 m in 20 s. Calculate power.
Step 1: Work = m g h = 40 × 10 × 10 = 4000 J
Step 2: Time = 20 s
Step 3: Power = 4000 / 20 = 200 W
✅ Answer: 200 W

Q31. Explain transformation of energy in:
(a) Hydroelectric power station
(b) Solar panel
(c) Thermal power station
✅ Answer:
Hydroelectric: PE → KE → Electrical
Solar panel: Solar → Electrical
Thermal station: Chemical (coal) → Heat → Steam KE → Electrical

Q32. A boy throws a ball of mass 200 g vertically upward with velocity 20 m/s. Find maximum height and potential energy at that point. (Take g = 10 m/s²)
Step 1: m = 0.2 kg, v = 20 m/s
Step 2: KE = ½ m v² = 0.1 × 400 = 40 J
Step 3: At top, PE = 40 J
Step 4: h = PE / (m g) = 40 / (0.2 × 10) = 20 m
✅ Answer: Height = 20 m, PE = 40 J

Q33. State and explain work-energy theorem with an example.
✅ Answer: Work done by net force = Change in KE. Example: Work done by brakes reduces KE of moving car.

Q34. A man of 60 kg climbs 20 steps, each of 0.2 m, in 30 s. Calculate power. (Take g = 9.8 m/s²)
Step 1: Height = 20 × 0.2 = 4 m
Step 2: Work = m g h = 60 × 9.8 × 4 = 2352 J
Step 3: Power = Work / time = 2352 / 30 ≈ 78.4 W
✅ Answer: 78.4 W

Q35. With suitable examples, explain:
(a) Positive work
(b) Negative work
(c) Zero work
✅ Answer:
Positive: Force and displacement same direction (engine pulls train).
Negative: Force and displacement opposite (friction).
Zero: Force perpendicular to displacement (gravity on satellite).

Section E – Case-Based (Q36 – Q39, 4 marks each)
Q36. A student lifts 15 kg of books to shelf 2 m high.
(a) Calculate work done.
(b) If done in 5 s, calculate power.
✅ Answer:
(a) W = m g h = 15 × 10 × 2 = 300 J
(b) P = 300 / 5 = 60 W

Q37. Observe: An electric heater of 1000 W is used for 3 h daily in a month.
(a) Find energy consumed.
(b) Express in kWh and Joules.
✅ Answer:
(a) Energy = 1000 × 3 × 30 = 90 000 Wh = 90 kWh
(b) = 90 × 3.6 × 10^6 = 3.24 × 10^8 J

Q38. A motor pulls 1000 kg of coal from a mine 100 m deep in 50 s.
Find:
(a) Work done
(b) Power
✅ Answer:
(a) W = m g h = 1000 × 10 × 100 = 1.0 × 10^6 J
(b) P = 1.0 × 10^6 / 50 = 20 000 W

Q39. A pendulum bob of mass 100 g is displaced so that it rises 5 cm above mean. Find potential energy at highest point and KE at mean.
✅ Answer:
(a) PE = m g h = 0.1 × 10 × 0.05 = 0.05 J
(b) KE at mean = 0.05 J

————————————————————————————————————————————————————————————————————————————

ONE PAGE REVISION SHEET

————————————————————————————————————————————————————————————————————————————

ACRONYMS

————————————————————————————————————————————————————————————————————————————

MISCONCEPTIONS “ALERTS”

————————————————————————————————————————————————————————————————————————————

KNOWLEDGE WITH FUN

————————————————————————————————————————————————————————————————————————————

MIND MAPS

————————————————————————————————————————————————————————————————————————————