Class : 9 – Science (English) : Lesson 7. Motion

EXPLANATION & SUMMARY

🔵 Detailed Explanation
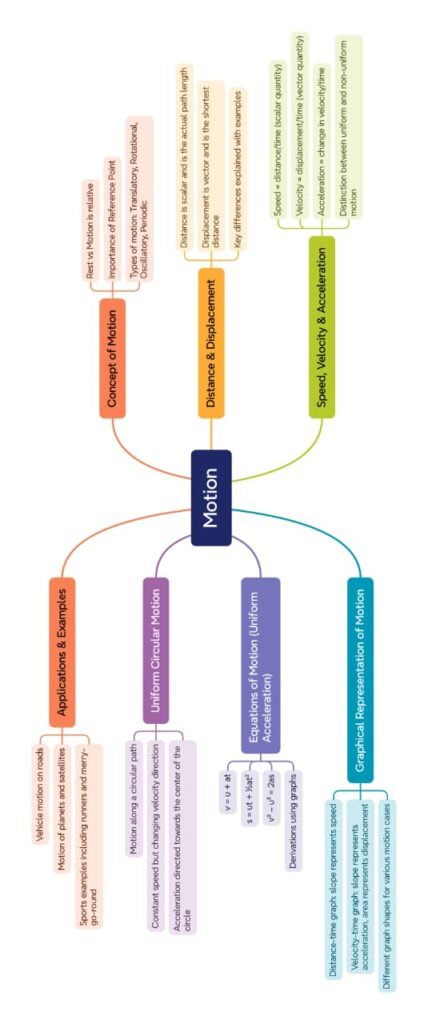
🌍 Introduction to Motion
Every object around us is either at rest or in motion.

🟢 Rest → an object is said to be at rest if its position does not change with time with respect to its surroundings.

🔵 Motion → an object is said to be in motion if it changes position with time relative to its surroundings.
Example: A bus moving on a road, a ball rolling on the ground.

🟡 Types of Motion
Rectilinear motion → motion in a straight line (car on straight road).
Circular motion → motion around a fixed point (fan blades).
Oscillatory motion → back-and-forth about mean position (pendulum).
Rotational motion → rotation around an axis (earth rotating on axis).

🟣 Distance and Displacement

🔵 Distance:
Total length of path covered.
Scalar quantity (magnitude only).
Always positive.

🟢 Displacement:
Shortest distance from initial to final position.
Vector quantity (magnitude + direction).
Can be zero if object returns to starting point.

💡 Example: If you walk 5 km east then 5 km west, distance = 10 km, displacement = 0.

⚡ Speed and Velocity
🔵 Speed:
Rate of change of distance.
Formula: speed = distance / time.
Scalar.

🟢 Velocity:
Rate of change of displacement.
Formula: velocity = displacement / time.
Vector.
✔️ Velocity can be zero if displacement = 0, even if speed ≠ 0.

🧠 Acceleration
Acceleration = change in velocity per unit time.
Formula: a = (v − u) / t
u = initial velocity
v = final velocity
t = time
Positive acceleration → speed increases.
Negative acceleration (deceleration) → speed decreases.

🌿 Uniform and Non-Uniform Motion
Uniform motion: equal distances in equal intervals of time (constant speed).
Non-uniform motion: unequal distances in equal intervals of time.

📊 Graphical Representation of Motion
Distance–time graph
Straight line → uniform motion.
Curve → non-uniform motion.
Horizontal line → object at rest.
Velocity–time graph
Straight line parallel to time axis → constant velocity.
Slope gives acceleration.
Area under curve gives displacement.

🟢 Equations of Motion (for uniform acceleration)
v = u + at
s = ut + ½ at²
v² − u² = 2as
✏️ Note: These are derived from velocity–time graphs.

💡 Uniform Circular Motion
When an object moves in a circle with uniform speed, its velocity changes direction continuously → hence it is accelerated motion.
Example: revolution of Earth around the Sun, satellites.

🟡 Real-Life Applications
Speedometer in vehicles measures instantaneous speed.
Navigation uses displacement and velocity.
Acceleration explains braking and pick-up in cars.
Graphs help in traffic and motion analysis.

🟢 Summary
Motion = change of position w.r.t. surroundings.
Distance (scalar) vs Displacement (vector).
Speed (scalar) vs Velocity (vector).
Acceleration = change in velocity/time.
Graphs show uniform/non-uniform motion.
Equations of motion (v = u + at, s = ut + ½ at², v² − u² = 2as).
Circular motion with constant speed is also accelerated.

📝 Quick Recap
🔵 Distance ≠ Displacement.
🟢 Speed ≠ Velocity.
🟡 Acceleration = (v−u)/t.
⚡ Equations of motion help calculate speed, distance, time.
🌍 Circular motion → speed constant, velocity changes due to direction.

————————————————————————————————————————————————————————————————————————————

QUESTIONS FROM TEXTBOOK

Question 1
An athlete completes one round of a circular track of diameter 200 m in 40 s. What will be the distance covered and the displacement at the end of 2 minutes 20 s?
Answer
Given: diameter = 200 m, time for 1 round = 40 s, total time = 2 min 20 s = 140 s.
Step 1 (circumference): C = π × d = π × 200 m = 200π m.
Step 2 (number of rounds): n = total time ÷ time per round = 140 s ÷ 40 s = 3.5 rounds.
Step 3 (distance): distance = n × C = 3.5 × 200π m = 700π m ≈ 2199 m.
Step 4 (displacement): after 3.5 rounds the athlete is at the point diametrically opposite the start, so displacement = diameter = 200 m (direction: along the straight line across the track).
Final: distance ≈ 2199 m; displacement = 200 m. 🔵

Question 2
Joseph jogs from one end A to the other end B of a straight 300 m road in 2 minutes 30 seconds and then turns around and jogs 100 m back to point C in another 1 minute. What are Joseph’s average speeds and velocities in jogging (a) from A to B and (b) from A to C?
Answer
(a) From A to B
Step 1 (distance): s = 300 m.
Step 2 (time): t = 2 min 30 s = 150 s.
Step 3 (average speed): v̄ = s ÷ t = 300 m ÷ 150 s = 2.0 m s⁻¹.
Step 4 (displacement): same as distance (straight line) = 300 m toward B.
Step 5 (average velocity): ū = displacement ÷ time = 300 m ÷ 150 s = 2.0 m s⁻¹ toward B.
Final (A→B): average speed = 2.0 m s⁻¹; average velocity = 2.0 m s⁻¹ toward B. 🟢
(b) From A to C
Step 1 (total distance): s = AB + BC(back) = 300 m + 100 m = 400 m.
Step 2 (total time): t = 150 s + 60 s = 210 s.
Step 3 (average speed): v̄ = s ÷ t = 400 m ÷ 210 s ≈ 1.9048 m s⁻¹.
Step 4 (displacement): AC = 200 m toward B.
Step 5 (average velocity): ū = displacement ÷ time = 200 m ÷ 210 s ≈ 0.9524 m s⁻¹ toward B.
Final (A→C): average speed ≈ 1.905 m s⁻¹; average velocity ≈ 0.952 m s⁻¹ toward B. 🟡

Question 3
Abdul, while driving to school, computes the average speed for his trip to be 20 km h⁻¹. On his return trip along the same route, there is less traffic and the average speed is 30 km h⁻¹. What is the average speed for Abdul’s trip?
Answer
Step 1 (let one-way distance) = L km.
Step 2 (total distance) = 2L km.
Step 3 (time going) = L ÷ 20 h.
Step 4 (time return) = L ÷ 30 h.
Step 5 (total time) = L ÷ 20 + L ÷ 30 = (3L + 2L) ÷ 60 = 5L ÷ 60 = L ÷ 12 h.
Step 6 (average speed) = total distance ÷ total time = 2L ÷ (L ÷ 12) = 24 km h⁻¹.
Final: average speed = 24 km h⁻¹. 🟣

Question 4
A motorboat starting from rest on a lake accelerates in a straight line at a constant rate of 3.0 m s⁻² for 8.0 s. How far does the boat travel during this time?
Answer
Step 1 (known): u = 0 m s⁻¹, a = 3.0 m s⁻², t = 8.0 s.
Step 2 (equation): s = ut + (1/2) a t².
Step 3 (substitute): s = 0 × 8 + 0.5 × 3.0 × (8)² m.
Step 4 (square time): (8)² = 64.
Step 5 (multiply): 0.5 × 3.0 × 64 = 1.5 × 64 = 96.
Final: distance s = 96 m. 🔴

Question 5
A driver of a car travelling at 52 km h⁻¹ applies the brakes.
(a) Shade the area on the graph that represents the distance travelled by the car during the period.
(b) Which part of the graph represents uniform motion of the car?
Answer
(a) Distance travelled = area under the speed–time curve between the instant brakes are applied and the instant the car stops; shade the region bounded by the curve and the time axis for that interval.
(b) The horizontal (flat) segment of the speed–time graph (where speed is constant at 52 km h⁻¹ before braking) represents uniform motion. 🟢

Question 6
Fig. 7.10 shows the distance–time graph of three objects A, B and C. Study the graph and answer the following questions:
(a) Which of the three is travelling the fastest?
(b) Are all three ever at the same point on the road?
(c) How far has C travelled when B passes A?
(d) How far has B travelled by the time it passes C?
Answer
(a) The object with the steepest slope (greatest rise per unit time) is the fastest; from the graph this is B.
(b) Check whether one single point is common to all three graphs; in Fig. 7.10 there is no single common intersection, so the answer is No.
(c) Read the distance coordinate at the intersection of A and B, then read C’s distance at the same time; that value is the answer for C (students should read exact km from their textbook graph).
(d) Read the distance coordinate at the intersection of B and C; that value is the distance travelled by B at that instant (again, read exact km from your graph).
🧠 Note: Because this is a read-from-graph problem, the precise numbers must be taken from the printed figure you have; method is shown step-by-step to ensure correct reading. 🔵

Question 7
A ball is gently dropped from a height of 20 m. If its velocity increases uniformly at the rate of 10 m s⁻², with what velocity will it strike the ground? After what time will it strike the ground?
Answer
Known: u = 0 m s⁻¹, a = 10 m s⁻², s = 20 m.
Part 1 (final velocity):
Step 1: v² = u² + 2 a s.
Step 2: v² = (0)² + 2 × 10 × 20 = 400.
Step 3: v = √400 = 20 m s⁻¹ (downward).
Part 2 (time of fall):
Step 4: v = u + a t.
Step 5: 20 = 0 + 10 t.
Step 6: t = 20 ÷ 10 = 2 s.
Final: velocity = 20 m s⁻¹ downward; time = 2 s. 🟡

Question 8
The speed–time graph for a car is shown in Fig. 7.11.
(a) Find how far the car travels in the first 4 seconds. Shade the area on the graph that represents the distance travelled by the car during the period.
(b) Which part of the graph represents uniform motion of the car?
Answer
(a) Distance in the first 4 s = area under the speed–time curve from t = 0 to t = 4 s.
Step 1: Read speeds from the graph at the required times (e.g., at 0 s, 2 s, 4 s).
Step 2: Compute the area using trapezium/rectangle counting or square counting method from your printed graph.
Step 3: Report the value in metres; this equals the distance in the first 4 s.
(b) The horizontal portion of the speed–time graph (where speed is constant) represents uniform motion. 🟣
🧠 Note: Exact numerical value depends on the plotted curve in your book; follow the shown steps to get the correct figure from your graph.

Question 9
State which of the following situations are possible and give an example for each of these:
(a) an object with a constant acceleration but with zero velocity
(b) an object moving with an acceleration but with uniform speed
(c) an object moving in a certain direction with an acceleration in the perpendicular direction
Answer
(a) Possible. Example: a ball thrown vertically upward at the highest point has velocity = 0 but acceleration = g downward (≈ 9.8 m s⁻²).
(b) Possible. Example: uniform circular motion at constant speed has acceleration toward the centre (direction changes).
(c) Possible. Example: A stone whirled in a horizontal circle has velocity tangential while acceleration (centripetal) is perpendicular toward the centre. 🔴

Question 10
An artificial satellite is moving in a circular orbit of radius 42 250 km. Calculate its speed if it takes 24 hours to revolve around the earth.
Answer
Step 1 (given): r = 42 250 km; T = 24 h.
Step 2 (formula): speed v = circumference ÷ time = (2πr) ÷ T.
Step 3 (circumference): 2πr = 2 × 3.1416 × 42 250 km = 265 465.2 km.
Step 4 (divide by time): v = 265 465.2 km ÷ 24 h = 11 061.05 km h⁻¹.
Step 5 (optional to m s⁻¹): v = 11 061.05 × (1000 m ÷ 3600 s) ≈ 3 072 m s⁻¹.
Final: speed ≈ 11 061 km h⁻¹ (≈ 3.07 × 10³ m s⁻¹). 🟢

————————————————————————————————————————————————————————————————————————————

OTHER IMPORTANT QUESTIONS FOR EXAMS

🔵 Section A (Q1–20: MCQs, 1 mark each; Q11–Q20 Assertion–Reason)
Question 1
The total path length covered by a body is called:
Distance
Displacement
Velocity
Acceleration
Answer: 1 🔵

Question 2
Which of the following is a vector quantity?
Speed
Distance
Velocity
Length
Answer: 3 🟢

Question 3
The slope of a distance–time graph gives:
Acceleration
Speed/Velocity
Displacement
Distance
Answer: 2 🟡

Question 4
Which of the following is possible for displacement but not for distance?
Always positive
Always greater than distance
Zero
Cannot be measured
Answer: 3 🔴

Question 5
A body is said to be in uniform motion when it:
Covers equal distances in equal intervals of time
Covers unequal distances in equal intervals
Does not change its position
Remains at rest
Answer: 1 🟣

Question 6
Which equation of motion does not involve time?
v = u + at
s = ut + ½ at²
v² − u² = 2as
s = (u + v)t/2
Answer: 3 🟠

Question 7
In uniform circular motion, acceleration is:
Zero
Along tangent
Toward centre
Away from centre
Answer: 3 🟤

Question 8
A car is moving with uniform speed. Which graph represents it correctly?
Distance–time straight line passing through origin
Distance–time curve bending upward
Velocity–time decreasing line
Distance constant
Answer: 1 🔵

Question 9
An object thrown upward has:
Constant acceleration upward
Constant acceleration downward
Increasing acceleration upward
No acceleration
Answer: 2 🟢

Question 10
The area under velocity–time graph gives:
Distance/Displacement
Speed
Acceleration
Force
Answer: 1 🟡

Question 11
Assertion (A): Speed is always positive.
Reason (R): Speed is the total distance covered per unit time.
Both A and R true, R correct explanation of A
Both A and R true, R not correct explanation
A true, R false
A false, R true
Answer: 1 🔴

Question 12
A: Displacement can be zero.
R: It depends on initial and final positions.
Answer: 1 🟣

Question 13
A: Slope of velocity–time graph gives acceleration.
R: Acceleration = Δv ÷ Δt.
Answer: 1 🟠

Question 14
A: Distance covered is always greater than or equal to displacement.
R: Displacement is shortest path.
Answer: 1 🟤

Question 15
A: Uniform speed means uniform velocity.
R: Direction of velocity may change.
Answer: 3 🔵

Question 16
A: A body thrown vertically upward has acceleration zero at top.
R: At the highest point velocity = 0.
Answer: 3 🟢 (acceleration is still g downward)

Question 17
A: Average velocity = (u + v)/2 if motion is uniformly accelerated.
R: Velocity changes linearly with time.
Answer: 1 🟡

Question 18
A: In uniform circular motion, speed is constant but velocity changes.
R: Direction of velocity changes continuously.
Answer: 1 🔴

Question 19
A: Equation s = ut + ½ at² applies only when acceleration is uniform.
R: Derivation assumes constant acceleration.
Answer: 1 🟣

Question 20
A: Negative acceleration means object slows down.
R: It is also called retardation.
Answer: 1 🟠

🟢 Section B (Q21–26: Very Short Answers, 2 marks)
Question 21
Define displacement.
Answer:
Shortest distance between initial and final positions in a specified direction. Vector quantity.

Question 22
State difference between speed and velocity.
Answer:
Speed = distance/time (scalar).
Velocity = displacement/time (vector).

Question 23
What is uniform motion?
Answer:
Equal distances in equal intervals of time, regardless of length of interval.

Question 24
Write SI units of speed, velocity, and acceleration.
Answer:
Speed → m s⁻¹
Velocity → m s⁻¹
Acceleration → m s⁻²

Question 25
What is retardation? Give example.
Answer:
Negative acceleration. Example: Car slowing down when brakes applied.

Question 26
Define average velocity.
Answer:
Average velocity = total displacement ÷ total time.

🟡 Section C (Q27–33: Short Answers, 3 marks)
Question 27
Differentiate between distance–time and displacement–time graphs.
Answer:
Distance–time graph: slope = speed.
Displacement–time graph: slope = velocity, can be negative.
Distance never decreases, displacement may.

Question 28
Derive v = u + at from velocity–time graph.
Answer:
Consider velocity–time graph: initial velocity u, final v after time t.
Acceleration a = (v − u)/t.
Rearrange: v = u + at.

Question 29
A bus starts from rest with acceleration 0.5 m s⁻². Find velocity after 10 s.
Answer:
u = 0, a = 0.5, t = 10.
v = u + at.
v = 0 + 0.5 × 10 = 5 m s⁻¹.

Question 30
Explain uniform circular motion as accelerated motion.
Answer:
Speed constant, but velocity changes continuously due to change in direction.
Acceleration directed towards centre (centripetal).

Question 31
Differentiate between uniform and non-uniform motion with example.
Answer:
Uniform: equal distances in equal times (car at 40 km h⁻¹).
Non-uniform: unequal distances (car in traffic).

Question 32
Write three equations of motion.
Answer:
v = u + at
s = ut + ½ at²
v² − u² = 2as

Question 33
State difference between scalar and vector quantities with examples.
Answer:
Scalar: only magnitude (speed, distance, mass).
Vector: magnitude + direction (velocity, force, displacement).

🔴 Section D (Q34–36: Long Answers, 5 marks)
Question 34
Derive s = ut + ½ at² using velocity–time graph.
Answer:
Draw velocity–time graph with initial velocity u, acceleration a, time t, final velocity v.
Distance = area under graph = rectangle (ut) + triangle (½ at²).
Hence, s = ut + ½ at².

Question 35
A train starting from rest attains velocity 72 km h⁻¹ in 5 min. Find acceleration and distance travelled.
Answer:
u = 0, v = 72 km h⁻¹ = 20 m s⁻¹, t = 5 min = 300 s.
Step 1 (acceleration): a = (v − u)/t = (20 − 0)/300 = 0.0667 m s⁻².
Step 2 (distance): s = ut + ½ at².
= 0 + 0.5 × 0.0667 × (300)².
= 0.0333 × 90 000 = 3000 m.
Final: acceleration = 0.0667 m s⁻²; distance = 3000 m.

Question 36
Explain graphical methods to find speed, velocity and acceleration.
Answer:
Distance–time slope = speed.
Displacement–time slope = velocity.
Velocity–time slope = acceleration.
Area under velocity–time graph = displacement.

🟣 Section E (Q37–39: Case-Based, 4 marks)
Question 37
Case: A car moves with uniform acceleration from rest. Its velocity after 10 s is 25 m s⁻¹.
(a) Find acceleration.
(b) Distance covered in this time.
(c) Which equation of motion is used?
(d) If motion continues, what will be velocity after 20 s?
Answer:
(a) a = (v − u)/t = (25 − 0)/10 = 2.5 m s⁻².
(b) s = ut + ½ at² = 0 + 0.5 × 2.5 × (10)² = 125 m.
(c) v = u + at, s = ut + ½ at².
(d) v = u + at = 0 + 2.5 × 20 = 50 m s⁻¹.

Question 38
Case: A ball is thrown vertically upward with speed 20 m s⁻¹.
(a) How high will it rise?
(b) Time to reach top?
(c) Total time of flight?
(d) Why acceleration is constant throughout?
Answer:
(a) v² = u² − 2gh = 0² = 20² − 2 × 9.8 × h → h = 400 ÷ 19.6 ≈ 20.4 m.
(b) v = u − g t → 0 = 20 − 9.8t → t = 2.04 s.
(c) Total time = 2 × 2.04 ≈ 4.08 s.
(d) Acceleration due to gravity is constant (9.8 m s⁻²) near Earth’s surface.

Question 39
Case: Graph-based question (velocity–time graph of a moving object).
(a) Which quantity is slope?
(b) Which is area under curve?
(c) If velocity–time graph is horizontal, what does it show?
(d) If graph slopes downward, what does it indicate?
Answer:
(a) Acceleration.
(b) Displacement.
(c) Constant velocity (uniform motion).
(d) Retardation/negative acceleration.

————————————————————————————————————————————————————————————————————————————

ONE PAGE REVISION SHEET

————————————————————————————————————————————————————————————————————————————

ACRONYMS

————————————————————————————————————————————————————————————————————————————

MISCONCEPTIONS “ALERTS”

————————————————————————————————————————————————————————————————————————————

KNOWLEDGE WITH FUN

————————————————————————————————————————————————————————————————————————————

MIND MAPS

————————————————————————————————————————————————————————————————————————————