Class : 9 – Math (English) : Lesson 11. Surface Areas and Volumes

EXPLANATION & SUMMARY

✨📖 EXPLANATION
🔵 1. Introduction
🧭 Geometry deals not only with plane figures but also with solid objects around us—cubes, cylinders, cones, spheres, hemispheres, and combinations of these.

🟢 Real-life applications: measuring paint for walls, steel for cylindrical tanks, water capacity of vessels, or volume of excavation for pits.
🔴 Two key aspects: Surface Area (outer covering) and Volume (space occupied).

🟡 2. Surface Areas of Solids
🔵 2.1 Surface Area of a Cube
📦 Cube: all edges equal, faces are squares.
📌 Lateral surface area (LSA) = 4a² (covers four vertical faces).
📌 Total surface area (TSA) = 6a² (all six faces).
💡 Example: A dice of edge = 5 cm → TSA = 6×(5²) = 150 cm².
🟢 2.2 Surface Area of a Cuboid
📦 Rectangular box with length l, breadth b, height h.
✔️ LSA = 2h(l + b).
✔️ TSA = 2(lb + bh + hl).
🟡 2.3 Surface Area of a Right Circular Cylinder
🏺 Cylinder with radius r, height h.
➡️ Curved surface area (CSA) = 2πrh.
➡️ TSA = 2πrh + 2πr² = 2πr(h + r).
✏️ Note: Two circular ends + curved area.
🔴 2.4 Surface Area of a Right Circular Cone
⛲ Cone with slant height l, base radius r.
📌 CSA = πrl.
📌 TSA = πr(l + r).
🟢 2.5 Surface Area of a Sphere
⚽ Perfectly round solid.
✔️ TSA = 4πr².
💡 Hemispheres: TSA = 3πr² (curved = 2πr² + base = πr²).
🟡 2.6 Surface Area of a Frustum of a Cone
✨ Formed by cutting a cone parallel to base.
Let radii be r₁ and r₂, slant height l.
✔️ CSA = πl(r₁ + r₂).
✔️ TSA = πl(r₁ + r₂) + πr₁² + πr₂².

🔵 3. Volumes of Solids
🟢 3.1 Volume of a Cuboid
🧊 V = l×b×h.
🟡 3.2 Volume of a Cube
🧊 V = a³.
🔴 3.3 Volume of a Cylinder
🏺 V = πr²h.
🟢 3.4 Volume of a Right Circular Cone
⛲ V = (1/3)πr²h.
🟡 3.5 Volume of a Sphere
⚽ V = (4/3)πr³.
✨ Hemisphere: V = (2/3)πr³.
🔵 3.6 Volume of a Frustum of a Cone
✏️ V = (1/3)πh(r₁² + r₂² + r₁r₂).

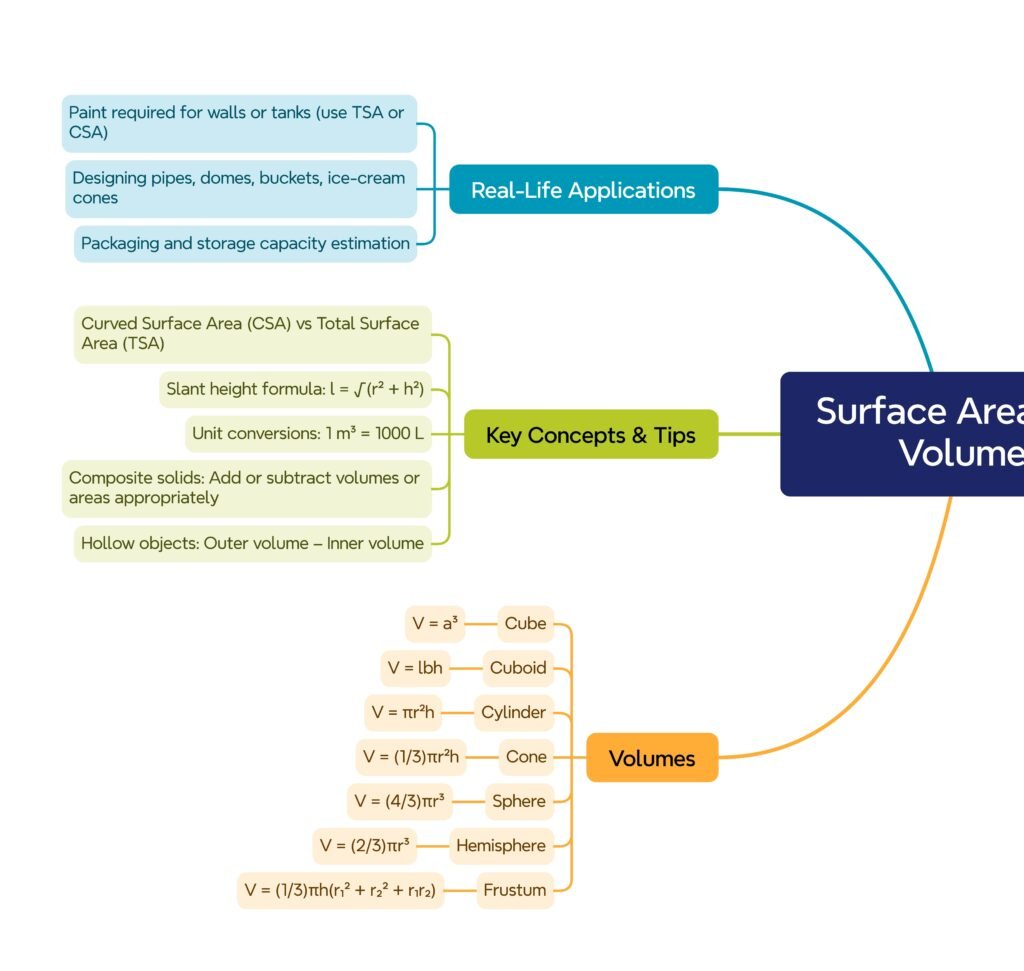
🟡 4. Conversions and Combinations
📌 Objects often combine basic solids: e.g., an ice-cream cone + hemisphere on top.
✔️ Break the object into simple solids, calculate surface areas or volumes separately, then add/subtract.
🟢 Hollow solids: volume = outer volume – inner volume.

🔴 5. Applications & Problem-Solving Tips
🧭 Paint or wrap: use TSA (or CSA if only curved part painted).
🧭 Capacity of tanks: use Volume.
🧭 Material removed: difference of volumes.
🧭 Metal sheet used: TSA excluding open ends if any.
✏️ Always convert units: cm²↔m² or cm³↔L (1 m³ = 1000 L).

🟢 6. Step-by-Step Solved Examples
📌 Example 1 – Cuboid Paint:
Given: l = 4 m, b = 3 m, h = 5 m. Find TSA.
➡️ TSA = 2(lb + bh + hl)
➡️ TSA = 2(4×3 + 3×5 + 5×4)
➡️ TSA = 2(12 + 15 + 20)
➡️ TSA = 2(47) = 94 m².
📌 Example 2 – Cone Volume:
r = 7 cm, h = 24 cm.
➡️ V = (1/3)πr²h
➡️ V = (1/3)π×49×24
➡️ V = (1/3)π×1176 = 392π cm³.
📌 Example 3 – Frustum:
r₁ = 10 cm, r₂ = 6 cm, h = 8 cm.
➡️ V = (1/3)πh(r₁² + r₂² + r₁r₂)
➡️ V = (1/3)π×8(100 + 36 + 60)
➡️ V = (8/3)π×196 = (1568/3)π cm³.
📌 Example 4 – Combination: Ice-cream = cone (r = 3 cm, h = 12 cm) + hemisphere (r = 3 cm).
➡️ V_total = (1/3)πr²h + (2/3)πr³
➡️ = (1/3)π×9×12 + (2/3)π×27
➡️ = 36π + 18π = 54π cm³.
📌 Example 5 – Hollow Pipe: Outer r = 7 cm, inner r = 5 cm, length = 40 cm. Find CSA.
➡️ CSA = 2πh(R + r) (h = length)
➡️ CSA = 2π×40(7 + 5)
➡️ = 2π×40×12 = 960π cm².

🔵 7. Common Mistakes to Avoid
❌ Mixing radius and diameter. Always halve diameter for radius.
❌ Forgetting to include/exclude bases depending on “open/closed” ends.
❌ Ignoring unit conversion (cm³ to m³ or liters).
❌ Adding areas of different units directly.

🟢 8. Real-Life Connections
🏗️ Civil engineering: estimating cement, sand, or paint.
🚀 Aerospace: calculating tank volumes.
📦 Packaging industry: designing boxes/cans to minimize material.
🏊 Pools & reservoirs: computing water capacities.

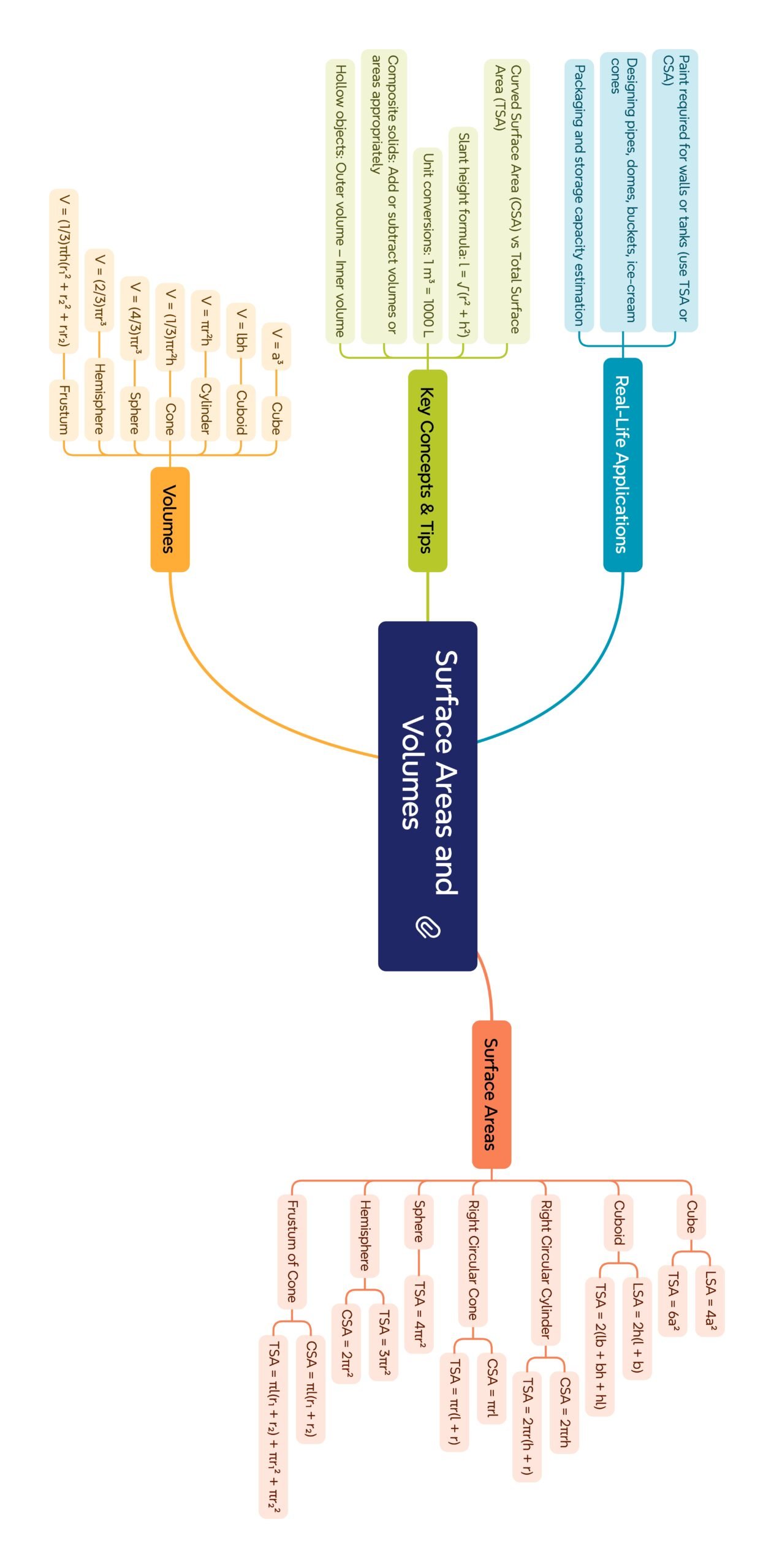
🟡 9. Key Formulas (Summary Table)
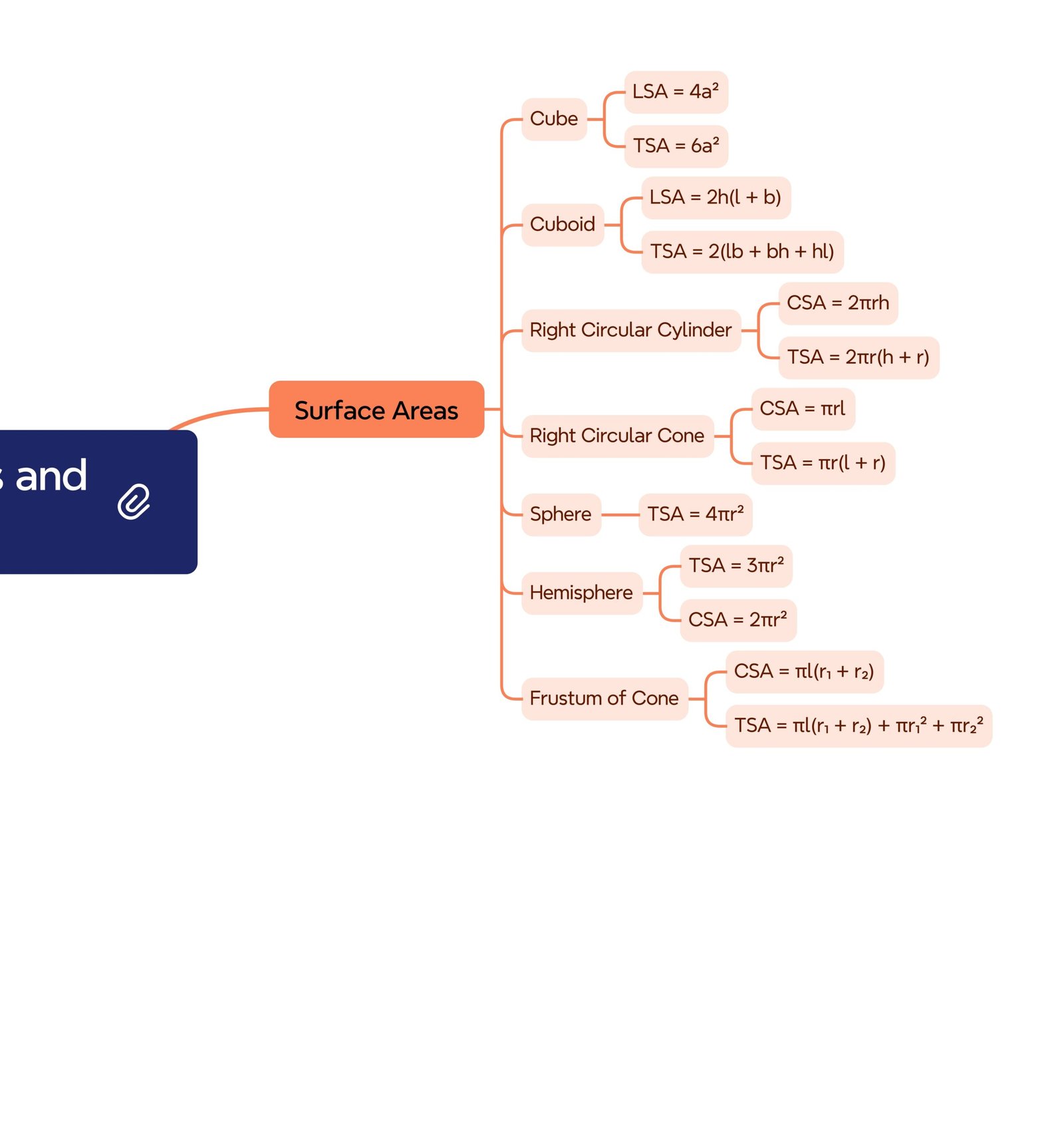
🔴 Surface Areas
Cube: LSA = 4a²; TSA = 6a².
Cuboid: LSA = 2h(l + b); TSA = 2(lb + bh + hl).
Cylinder: CSA = 2πrh; TSA = 2πr(h + r).
Cone: CSA = πrl; TSA = πr(l + r).
Sphere: 4πr²; Hemisphere: 3πr².
Frustum: CSA = πl(r₁ + r₂); TSA = πl(r₁ + r₂) + πr₁² + πr₂².
🔵 Volumes
Cube: a³.
Cuboid: lbh.
Cylinder: πr²h.
Cone: (1/3)πr²h.
Sphere: (4/3)πr³.
Hemisphere: (2/3)πr³.
Frustum: (1/3)πh(r₁² + r₂² + r₁r₂).

🌟 SUMMARY (~300 words)
🧭 The chapter explores 3-D geometry of cubes, cuboids, cylinders, cones, spheres, hemispheres, and frustums.
🔵 Surface area measures the total outer covering; volume measures the capacity or space occupied.
🟢 Cubes/cuboids: TSA formulas involve squares and rectangles; widely used in packaging and construction.
🟡 Cylinders: Think water tanks or pipes; CSA covers curved part only, TSA includes two circular bases.
🔴 Cones: Slant height l critical for CSA = πrl. Frustum formulas used for bucket-shaped objects.
🟢 Spheres/hemispheres: Key in sports balls, globes, bubbles; remember TSA = 4πr², V = (4/3)πr³.
🟡 Hollow and combination solids: subtract or add volumes appropriately.
✔️ Always convert units correctly and read “open” or “closed” hints in problems.
💡 Real-world connections: estimating paint, wrapping gifts, designing tanks, pipes, ice-cream cones, or storage containers.
🧭 Practice ensures accuracy: break complex figures into basic solids.
🌟 Understanding these formulas equips students to solve practical engineering, architecture, and design problems effectively.

📝 QUICK RECAP (5 Bullets)
📦 Cube/Cuboid – TSA: 6a² / 2(lb + bh + hl); Volumes: a³ / lbh.
🏺 Cylinder/Cone – CSA: 2πrh / πrl; TSA includes bases; Volumes: πr²h / (1/3)πr²h.
⚽ Sphere/Hemisphere – TSA: 4πr² / 3πr²; Volumes: (4/3)πr³ / (2/3)πr³.
✨ Frustum – CSA: πl(r₁ + r₂); Volume: (1/3)πh(r₁² + r₂² + r₁r₂).
🧭 Tips – Check units, distinguish CSA/TSA, split composites, and apply real-world context.

———————————————————————————————————————————————————————————————————————————–

TEXT BOOK QUESTIONS

Exercise 11.1

🔵 Question 1
Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
🟢 Answer
➡️ Radius r = 10.5 ÷ 2 = 5.25 cm
➡️ Slant height l = 10 cm
➡️ CSA = π r l = (22/7) × 5.25 × 10
➡️ 5.25 = 21/4 ⇒ CSA = (22/7) × (21/4) × 10
➡️ CSA = (22 × 21 × 10) ÷ 28 = 4620 ÷ 28 = 165 cm²

🔵 Question 2
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
🟢 Answer
➡️ r = 24 ÷ 2 = 12 m
➡️ l = 21 m
➡️ TSA = π r (l + r) = (22/7) × 12 × (21 + 12)
➡️ = (22/7) × 12 × 33 = (22 × 12 × 33) ÷ 7 = 8712 ÷ 7 = 1244.57 m² ≈ 1245 m²

🔵 Question 3
Curved surface area of a cone is 308 cm² and its slant height is 14 cm. Find
(i) radius of the base
(ii) total surface area of the cone.
🟢 Answer
➡️ CSA = π r l = 308, l = 14
➡️ r = 308 ÷ ((22/7) × 14) = 308 × 7 ÷ (22 × 14) = 2156 ÷ 308 = 7 cm ✔ (i)
➡️ TSA = π r (l + r) = (22/7) × 7 × (14 + 7)
➡️ = 22 × 21 = 462 cm² ✔ (ii)

🔵 Question 4
A conical tent is 10 m high and the radius of its base is 24 m. Find
(i) slant height of the tent.
(ii) cost of the canvas required to make the tent, if the cost of 1 m² canvas is ₹ 70.
🟢 Answer
➡️ r = 24 m, h = 10 m
➡️ l = √(r² + h²) = √(24² + 10²) = √(576 + 100) = √676 = 26 m ✔ (i)
➡️ CSA = π r l = (22/7) × 24 × 26 = 13728 ÷ 7 = 1961.14 m²
➡️ Cost = 1961.14 × 70 ≈ ₹ 137,280 ✔ (ii)

🔵 Question 5
What length of tarpaulin 3 m wide will be required to make a conical tent of height 8 m and base radius 6 m? Assume extra length of 0.20 m for margins and wastage.
🟢 Answer
➡️ r = 6 m, h = 8 m
➡️ l = √(6² + 8²) = √(36 + 64) = √100 = 10 m
➡️ CSA = π r l = (22/7) × 6 × 10 = 1320 ÷ 7 ≈ 188.57 m²
➡️ Required length = CSA ÷ width = 188.57 ÷ 3 ≈ 62.86 m
➡️ Total length = 62.86 + 0.20 = 63.06 m ≈ 63.1 m

🔵 Question 6
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at ₹ 210 per 100 m².
🟢 Answer
➡️ r = 14 ÷ 2 = 7 m, l = 25 m
➡️ CSA = π r l = (22/7) × 7 × 25 = 550 m²
➡️ Cost per m² = 210 ÷ 100 = ₹ 2.10
➡️ Total cost = 550 × 2.10 = ₹ 1155

🔵 Question 7
A joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
🟢 Answer
➡️ r = 7 cm, h = 24 cm
➡️ l = √(7² + 24²) = √(49 + 576) = √625 = 25 cm
➡️ CSA (one cap) = π r l = (22/7) × 7 × 25 = 550 cm²
➡️ For 10 caps = 10 × 550 = 5500 cm²

🔵 Question 8
A bus stop is barricaded using 50 hollow cones of base diameter 40 cm and height 1 m. The outer surface of each cone is painted at ₹ 12 per m². Find the total cost. (Use π = 3.14, √1.04 = 1.02)
🟢 Answer
➡️ Diameter = 40 cm ⇒ r = 20 cm = 0.20 m
➡️ h = 1 m
➡️ l = √(h² + r²) = √(1² + 0.20²) = √1.04 ≈ 1.02 m
➡️ CSA (one) = π r l = 3.14 × 0.20 × 1.02 ≈ 0.64056 m²
➡️ For 50 cones = 50 × 0.64056 = 32.028 m²
➡️ Cost = 32.028 × 12 ≈ ₹ 384.34 ≈ ₹ 384

Exercise 11.2

🔵 Question 1
Find the surface area of a sphere of radius:
(i) 10.5 cm (ii) 5.6 cm (iii) 14 cm
🟢 Answer
➡️ Formula: TSA = 4 π r²
(i) r = 10.5 cm → TSA = 4 × (22/7) × 10.5² = 4 × (22/7) × 110.25 = 4 × 22 × 15.75 = 1386 cm²
(ii) r = 5.6 cm → TSA = 4 × (22/7) × 5.6² = 4 × (22/7) × 31.36 = 4 × 22 × 4.48 = 394.24 cm²
(iii) r = 14 cm → TSA = 4 × (22/7) × 14² = 4 × (22/7) × 196 = 4 × 22 × 28 = 2464 cm²

🔵 Question 2
Find the surface area of a sphere of diameter:
(i) 14 cm (ii) 21 cm (iii) 3.5 m
🟢 Answer
➡️ r = d ÷ 2
(i) d = 14 cm → r = 7 cm → TSA = 4 π r² = 4 × (22/7) × 7² = 4 × (22/7) × 49 = 4 × 22 × 7 = 616 cm²
(ii) d = 21 cm → r = 10.5 cm → TSA = 4 × (22/7) × 10.5² = 4 × (22/7) × 110.25 = 4 × 22 × 15.75 = 1386 cm²
(iii) d = 3.5 m → r = 1.75 m → TSA = 4 × (22/7) × 1.75² = 4 × (22/7) × 3.0625 = 4 × 22 × 0.4375 = 38.5 m²

🔵 Question 3
Find the total surface area of a hemisphere of radius 10 cm. (Use π = 3.14)
🟢 Answer
➡️ TSA(hemisphere) = 3 π r²
➡️ = 3 × 3.14 × 10² = 3 × 3.14 × 100 = 942 cm²

🔵 Question 4
The radius of a spherical balloon increases from 7 cm to 14 cm as air is pumped in. Find the ratio of surface areas.
🟢 Answer
➡️ TSA ∝ r²
➡️ Ratio = 7² : 14² = 49 : 196 = 1 : 4

🔵 Question 5
A hemispherical bowl of brass has inner diameter 10.5 cm. Find the cost of tin-plating its inside at ₹ 16 per 100 cm².
🟢 Answer
➡️ r = 10.5 ÷ 2 = 5.25 cm
➡️ CSA(hemisphere) = 2 π r² = 2 × (22/7) × 5.25² = 2 × (22/7) × 27.5625 = 2 × 22 × 3.9375 = 173.25 cm²
➡️ Cost rate = ₹ 16 per 100 cm² = ₹ 0.16 per cm²
➡️ Cost = 173.25 × 0.16 ≈ ₹ 27.72 ≈ ₹ 28

🔵 Question 6
Find the radius of a sphere whose surface area is 154 cm².
🟢 Answer
➡️ TSA = 4 π r² = 154
➡️ r² = 154 ÷ (4 π) = 154 ÷ (4 × 22/7) = 154 × 7 ÷ 88 = 1078 ÷ 88 = 12.25
➡️ r = √12.25 = 3.5 cm

🔵 Question 7
The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface areas.
🟢 Answer
➡️ r_moon : r_earth = 1 : 4
➡️ Surface area ∝ r² → Ratio = (1)² : (4)² = 1 : 16

🔵 Question 8
A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius is 5 cm. Find the outer curved surface area of the bowl.
🟢 Answer
➡️ r_inner = 5 cm, thickness = 0.25 cm → r_outer = 5 + 0.25 = 5.25 cm
➡️ CSA_outer = 2 π r_outer² = 2 × (22/7) × (5.25)² = 2 × (22/7) × 27.5625 = 2 × 22 × 3.9375 = 173.25 cm²

🔵 Question 9
A right circular cylinder just encloses a sphere of radius r. Find
(i) surface area of the sphere,
(ii) curved surface area of the cylinder,
(iii) ratio of the areas obtained in (i) and (ii).
🟢 Answer
➡️ Sphere radius = r
➡️ Cylinder just encloses sphere → diameter = height → h = 2r, base radius = r
(i) TSA_sphere = 4 π r²
(ii) CSA_cylinder = 2 π r h = 2 π r (2r) = 4 π r²
(iii) Ratio = 4 π r² : 4 π r² = 1 : 1

Exercise 11.3

🔵 Question 1
Find the volume of the right circular cone with
(i) r = 6 cm, h = 7 cm (ii) r = 3.5 cm, h = 12 cm
🟢 Answer
➡️ Formula: V = (1/3) π r² h
(i) V = (1/3) × (22/7) × 6² × 7 = (1/3) × (22/7) × 36 × 7
➡️ V = (1/3) × 22 × 36 = 264 cm³
(ii) V = (1/3) × (22/7) × (3.5)² × 12 = (1/3) × (22/7) × 12.25 × 12
➡️ = (1/3) × 22 × 1.75 × 12 = (1/3) × 462 = 154 cm³

🔵 Question 2
Find the capacity in litres of a conical vessel with
(i) r = 7 cm, l = 25 cm (ii) h = 12 cm, l = 13 cm
🟢 Answer
➡️ Use V = (1/3) π r² h, convert cm³ to litres (1 L = 1000 cm³).
(i) h = √(l² – r²) = √(25² – 7²) = √(625 – 49) = √576 = 24 cm
➡️ V = (1/3) × (22/7) × 7² × 24 = (1/3) × (22/7) × 49 × 24
➡️ = (1/3) × 22 × 7 × 24 = (1/3) × 3696 = 1232 cm³ = 1.232 L
(ii) r = √(l² – h²) = √(13² – 12²) = √(169 – 144) = √25 = 5 cm
➡️ V = (1/3) × (22/7) × 5² × 12 = (1/3) × (22/7) × 25 × 12
➡️ = (1/3) × (22 × 25 × 12 /7) = (1/3) × 6600/7 = 2200/7 ≈ 314.29 cm³ = 0.314 L

🔵 Question 3
The height of a cone is 15 cm. Its volume is 1570 cm³. Find the radius. (Use π = 3.14)
🟢 Answer
➡️ V = (1/3) π r² h = 1570
➡️ r² = (3 × 1570)/(3.14 × 15) = 4710/47.1 = 100
➡️ r = √100 = 10 cm

🔵 Question 4
If the volume of a right circular cone of height 9 cm is 48π cm³, find the diameter of its base.
🟢 Answer
➡️ V = (1/3) π r² h = 48π
➡️ (1/3) × π × r² × 9 = 48π
➡️ 3π r² = 48π
➡️ r² = 16 ⇒ r = 4 cm
➡️ Diameter = 2r = 8 cm

🔵 Question 5
A conical pit of top diameter 3.5 m is 12 m deep. Find its capacity in kilolitres.
🟢 Answer
➡️ r = 3.5/2 = 1.75 m, h = 12 m
➡️ V = (1/3) π r² h = (1/3) × (22/7) × (1.75)² × 12
➡️ = (1/3) × (22/7) × 3.0625 × 12
➡️ = (1/3) × 22 × 0.4375 × 12 = (1/3) × 115.5 = 38.5 m³ = 38.5 kL

🔵 Question 6
The volume of a right circular cone is 9856 cm³. If the diameter of the base is 28 cm, find
(i) height (ii) slant height (iii) curved surface area
🟢 Answer
➡️ r = 28/2 = 14 cm
(i) V = (1/3) π r² h = 9856
➡️ h = (3 × 9856)/(π r²) = 29568 / ((22/7) × 196)
➡️ = 29568 / 616 = 48 cm
(ii) l = √(r² + h²) = √(14² + 48²) = √(196 + 2304) = √2500 = 50 cm
(iii) CSA = π r l = (22/7) × 14 × 50 = 2200 cm²

🔵 Question 7
A right triangle ABC with sides 5 cm, 12 cm, 13 cm is revolved about side 12 cm. Find the volume of the solid so obtained.
🟢 Answer
➡️ When revolved about side 12 cm, radius = 5 cm, height = 12 cm
➡️ V = (1/3) π r² h = (1/3) π × 5² × 12 = (1/3) π × 25 × 12 = 100π cm³ ≈ 314.16 cm³

🔵 Question 8
If triangle ABC in Question 7 is revolved about side 5 cm, find
(i) the volume of the solid obtained (ii) ratio of volumes of Q7 and Q8
🟢 Answer
➡️ Now radius = 12 cm, height = 5 cm
(i) V = (1/3) π r² h = (1/3) π × 12² × 5 = (1/3) π × 144 × 5 = 240π cm³ ≈ 753.98 cm³
(ii) Ratio = V(Q7) : V(Q8) = 100π : 240π = 5 : 12

🔵 Question 9
A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume and the area of canvas needed to cover it.
🟢 Answer
➡️ r = 10.5/2 = 5.25 m, h = 3 m
➡️ V = (1/3) π r² h = (1/3) × (22/7) × (5.25)² × 3
➡️ = (1/3) × (22/7) × 27.5625 × 3 = (22/7) × 27.5625 = 86.625 m³
➡️ l = √(r² + h²) = √(5.25² + 3²) = √(27.5625 + 9) = √36.5625 ≈ 6.05 m
➡️ CSA = π r l = (22/7) × 5.25 × 6.05 ≈ 99.9 m²

Exercise 11.4

🔵 Question 1
Find the volume of a sphere whose radius is
(i) 7 cm (ii) 0.63 m
🟢 Answer
➡️ Formula: V = (4/3) π r³
(i) r = 7 cm
V = (4/3) × (22/7) × 7³
= (4/3) × (22/7) × 343
= (4/3) × 22 × 49
= (88 × 49)/3
= 4312/3 ≈ 1437.33 cm³ (≈ 1.44 L)
(ii) r = 0.63 m
r³ = 0.63³ = 0.250047
V = (4/3) × π × 0.250047
≈ (4/3) × 3.1416 × 0.250047
= 1.0472 × 0.250047
≈ 0.262 m³ (≈ 262 L)

🔵 Question 2
Find the amount of water displaced by a solid spherical ball of diameter
(i) 28 cm (ii) 0.21 m
🟢 Answer
➡️ r = d/2
(i) r = 14 cm
V = (4/3) π r³ = (4/3) × (22/7) × 14³
= (4×22×2744)/(21)
= (24064)/(21) ≈ 11498.7 cm³ (≈ 11.5 L)
(ii) r = 0.105 m
V = (4/3) π r³ = (4/3) × π × 0.105³
= (4/3) × π × 0.001157
= 0.00485 m³ (≈ 4.85 L)

🔵 Question 3
The diameter of a metallic ball is 4.2 cm. Find its mass if the density is 8.9 g/cm³.
🟢 Answer
➡️ r = 4.2/2 = 2.1 cm
V = (4/3) π r³ = (4/3) × (22/7) × 2.1³
= (4/3) × (22/7) × 9.261
= (4×22×1.323)/3
= 116.424/3 = 38.81 cm³
Mass = Density × Volume = 8.9×38.81 ≈ 345.4 g

🔵 Question 4
The diameter of the moon is ¼ of the Earth’s diameter. Find the fraction of Earth’s volume that is the moon’s.
🟢 Answer
➡️ Volume ∝ r³
Fraction = (1/4)³ = 1/64

🔵 Question 5
How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold?
🟢 Answer
➡️ r = 10.5/2 = 5.25 cm
V = (2/3) π r³ = (2/3) × (22/7) × 5.25³
= (2/3) × (22/7) × 144.7
= (2×22×20.671)/3 = 909.5/3 = 303.2 cm³
= 0.303 L

🔵 Question 6
A hemispherical tank is made of an iron sheet 1 cm thick. Inner radius = 1 m. Find the volume of iron used.
🟢 Answer
➡️ r_inner = 1 m
r_outer = 1 + 0.01 = 1.01 m
V = (2/3) π (r_outer³ − r_inner³)
= (2/3) π (1.01³ − 1³)
1.01³ ≈ 1.030301 → Difference = 0.030301
V = (2/3) π × 0.030301 = 0.0202 π ≈ 0.0635 m³ (≈ 63.5 L)

🔵 Question 7
Find the volume of a sphere whose surface area is 154 cm².
🟢 Answer
➡️ 4 π r² = 154
r² = 154/(4 π) = 154/(4×22/7) = 1078/88 = 12.25
r = √12.25 = 3.5 cm
V = (4/3) π r³ = (4/3) π (3.5³) = (4/3) π 42.875
= 57.167 π ≈ 179.6 cm³

🔵 Question 8
A dome of a building is in the form of a hemisphere. From inside, it was white-washed at ₹ 4989.60. If the cost is ₹ 20/m², find
(i) inside surface area (ii) volume of air inside.
🟢 Answer
(i) CSA = Cost/Rate = 4989.60/20 = 249.48 m²
2 π r² = 249.48
r² = 249.48/(2 π) = 249.48/6.283 = 39.72
r = √39.72 = 6.30 m
(ii) V = (2/3) π r³ = (2/3) π 6.30³ = (2/3) π 250
= (500/3) π ≈ 523.6 m³

🔵 Question 9
Twenty spheres each of radius r are melted to form a sphere of surface area S′. Find the new radius r′ and ratio S/S′.
🟢 Answer
20 × (4/3) π r³ = (4/3) π r′³
20 r³ = r′³
r′ = 20^(1/3) r ≈ 2.714 r
S = 20×4 π r² = 80 π r²
S′ = 4 π r′² = 4 π 20^(2/3) r² ≈ 4 π 7.367 r² = 29.47 π r²
Ratio S/S′ = 80 π r² / 29.47 π r² ≈ 2.71:1

🔵 Question 10
A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. Find the volume of medicine needed.
🟢 Answer
r = 3.5/2 = 1.75 mm
V = (4/3) π r³ = (4/3) π 1.75³
= (4/3) π 5.36
= 7.147 π ≈ 22.45 mm³

———————————————————————————————————————————————————————————————————————————–

OTHER IMPORTANT QUESTIONS FOR EXAMS

🌟 SECTION A – 1 Mark Each
🔵 Question 1
Find the curved surface area of a cone with r = 7 cm and l = 25 cm.
🟢 Answer
CSA = π r l = (22/7)×7×25 = 550 cm²

🔵 Question 2
Find the total surface area of a sphere of diameter 14 cm.
🟢 Answer
r = 7 cm
TSA = 4πr² = 4×(22/7)×7² = 4×22×7 = 616 cm²

🔵 Question 3
The volume of a cone is 154 cm³ and its height is 7 cm. Find the radius.
🟢 Answer
V = (1/3)πr²h ⇒ r² = (3×154)/(π×7) = 462/(22/7×7) = 462/22 = 21 ⇒ r = √21 ≈ 4.58 cm

🔵 Question 4
A hemispherical bowl of radius 3.5 cm is completely filled with water. Find the volume.
🟢 Answer
V = (2/3)πr³ = (2/3)×(22/7)×3.5³ = (2/3)×(22/7)×42.875 = 88/21×42.875 ≈ 179.5 cm³

🔵 Question 5
Find the surface area of a sphere whose volume is 36π cm³.
🟢 Answer
V = (4/3)πr³ = 36π ⇒ r³ = 27 ⇒ r = 3 cm
TSA = 4πr² = 4π×9 = 36π cm²

🔵 Question 6
Find the height of a cone whose slant height is 10 cm and base radius is 6 cm.
🟢 Answer
h = √(l² − r²) = √(10² − 6²) = √(100 − 36) = √64 = 8 cm

🌟 SECTION B – 2 Marks Each
🔵 Question 7
Find the capacity of a conical vessel with r = 5 cm, h = 12 cm. Express in litres.
🟢 Answer
V = (1/3)πr²h = (1/3)π×25×12 = 100π ≈ 314.16 cm³ = 0.314 L

🔵 Question 8
Find the curved surface area of a hemisphere of radius 7 cm.
🟢 Answer
CSA = 2πr² = 2×(22/7)×7² = 2×22×7 = 308 cm²

🔵 Question 9
The volume of a sphere is 288π cm³. Find its radius.
🟢 Answer
V = (4/3)πr³ = 288π ⇒ r³ = 216 ⇒ r = 6 cm

🔵 Question 10
A cone has height 24 cm and base radius 7 cm. Find its slant height and CSA.
🟢 Answer
l = √(h² + r²) = √(24² + 7²) = √(576 + 49) = √625 = 25 cm
CSA = π r l = (22/7)×7×25 = 550 cm²

🔵 Question 11
A solid sphere of radius 3 cm is melted to form small spheres of radius 1 cm. Find the number of small spheres.
🟢 Answer
V_big = (4/3)π3³ = 36π
V_small = (4/3)π1³ = (4/3)π
Number = 36π ÷ (4/3)π = 27

🔵 Question 12
Find the diameter of a sphere whose surface area is 154 cm².
🟢 Answer
4πr² = 154 ⇒ r² = 154/(4π) = 154/(4×22/7)=1078/88=12.25 ⇒ r=3.5 cm ⇒ Diameter=7 cm

🌟 SECTION C – 3 Marks Each (Internal Choices Included)
🔵 Question 13
Find the volume of a hemisphere of radius 10.5 cm.
🟢 Answer
V=(2/3)πr³=(2/3)×(22/7)×10.5³=(2/3)×(22/7)×1157.625=(2×22×165.375)/3=7266.5/3≈2422.2 cm³

🔵 Question 14
A conical tent is 10 m high and radius of base is 24 m. Find the cost of canvas at ₹70/m².
🟢 Answer
l=√(24²+10²)=√676=26 m
CSA=π r l=(22/7)×24×26=1961.14 m²
Cost=1961.14×70≈₹137,280

🔵 Question 15 (OR)
Find the capacity in litres of a sphere of diameter 42 cm.
🟢 Answer
r=21 cm
V=(4/3)πr³=(4/3)π21³=(4/3)π9261=12348π≈38799 cm³=38.8 L

🔵 Question 16
The slant height and base diameter of a conical tomb are 25 m and 14 m. Find cost of whitewashing at ₹210/100 m².
🟢 Answer
r=7 m
CSA=πrl=(22/7)×7×25=550 m²
Rate=₹2.10/m² ⇒ Cost=550×2.10=₹1155

🔵 Question 17
Find the volume of a cone whose volume equals a hemisphere of radius 7 cm and height = 3r. Verify.
🟢 Answer
V_hemi=(2/3)π7³=686.67π
Set (1/3)πr²h=686.67π, h=3r → (1/3)πr²×3r=πr³=686.67π ⇒ r³=686.67 ⇒ r=8.8 cm (approx)

🔵 Question 18 (OR)
A hemispherical bowl is made of steel 0.25 cm thick, inner radius=5 cm. Find volume of metal used.
🟢 Answer
r_outer=5.25 cm
V=(2/3)π(r³_outer−r³_inner)=(2/3)π(144.7−125)=(2/3)π19.7=41.3 cm³

🔵 Question 19
A capsule medicine shaped as sphere, diameter=3.5 mm. Find volume.
🟢 Answer
r=1.75 mm
V=(4/3)πr³=(4/3)π(5.36)=7.15π≈22.45 mm³

🔵 Question 20
The diameter of the moon is ¼ of Earth’s. Find fraction of Earth’s volume that is moon’s.
🟢 Answer
(1/4)³=1/64

🔵 Question 21 (OR)
Find r of a sphere whose TSA=616 cm².
🟢 Answer
4πr²=616 ⇒ r²=616/(4π)=616/(4×22/7)=1078/44=24.5 ⇒ r=√24.5=4.95 cm

🔵 Question 22
A right triangle ABC with sides 5,12,13 revolved about side 12. Find volume.
🟢 Answer
r=5,h=12 ⇒ V=(1/3)πr²h=(1/3)π25×12=100π≈314.16 cm³

🌟 SECTION D – 4 Marks Each (Internal Choices)
🔵 Question 23
A heap of wheat is a cone diameter=10.5 m,height=3 m. Find volume and canvas area.
🟢 Answer
r=5.25,l=√(5.25²+3²)=6.05 m
V=(1/3)πr²h=(1/3)(22/7)(5.25²)(3)=86.6 m³
CSA=πrl=(22/7)(5.25)(6.05)=99.9 m²

🔵 Question 24 (OR)
Find radius of sphere whose volume is 179.6 cm³.
🟢 Answer
V=(4/3)πr³=179.6 ⇒ r³=179.6×3/(4π)=539/12.566=42.9 ⇒ r=3.5 cm

🔵 Question 25
Twenty spheres each of radius r melted to form sphere radius r′. Find r′ and ratio of surface areas.
🟢 Answer
20r³=r′³ ⇒ r′=20^1/3r≈2.714r
S=80πr²,S′=4πr′²=4π20^(2/3)r²≈29.47πr²
Ratio S/S′=80/29.47=2.71:1

🔵 Question 26
A dome hemisphere painted inside costs ₹2498. If rate ₹20/m², find radius and volume.
🟢 Answer
CSA=2498/20=124.9 ⇒2πr²=124.9 ⇒r²=124.9/(2π)=19.88⇒r=4.46 m
V=(2/3)πr³=(2/3)π88.7=185.9 m³

🔵 Question 27 (OR)
Find slant height and CSA of cone h=24 cm,r=7 cm.
🟢 Answer
l=√(24²+7²)=√625=25 cm
CSA=πrl=(22/7)(7)(25)=550 cm²

🔵 Question 28
A hemispherical tank made of sheet thickness 0.01 m,inner radius=1 m. Find volume of sheet.
🟢 Answer
r_outer=1.01 ⇒V=(2/3)π(1.01³−1³)=(2/3)π(0.0303)=0.0202π≈0.0635 m³

🔵 Question 29
Find height of cone volume=308 cm³,r=7 cm.
🟢 Answer
V=(1/3)πr²h=308 ⇒h=308×3/(π×49)=924/(22/7×49)=924/154=6 cm

🔵 Question 30 (OR)
A sphere of radius 3 cm is melted into cones r=3 cm,h=4 cm. Find number of cones.
🟢 Answer
V_sphere=(4/3)π3³=36π
V_cone=(1/3)π3²×4=12π
Number=36π/12π=3

————————————————————————————————————————————————————————————————————————————

MIND MAP

———————————————————————————————————————————————————————————————————————————–