Class : 9 – Math (English) : Lesson 9. Circles

Posted by

On June 16, 2025

EXPLANATION & SUMMARY

✨ Explanation
🔵 1) What is a Circle? (Core idea)
🧠 A circle is the set of all points in a plane that are at a fixed distance (called the radius) from a fixed point (called the centre).

🟢 Notation and basic terms:
➡️ Centre: O
➡️ Radius: any segment like OA with length r
➡️ Diameter: any chord through O; length 2r
➡️ Circumference: complete boundary of the circle
➡️ Chord: a segment joining two points on the circle (AB)
➡️ Arc: part of the circle between two points (minor arc, major arc)
➡️ Sector: region enclosed by two radii and the included arc (minor sector, major sector)
➡️ Segment: region enclosed by a chord and the corresponding arc (minor segment, major segment)
✏️ Note: Every diameter is a chord, but not every chord is a diameter.
💡 Concept: For any circle, all radii are equal and all diameters are equal (= 2r). This single fact powers many proofs.
🔵 2) Types of Circles & Relative Position
🟢 Congruent circles: circles having equal radii.
🟢 Concentric circles: circles with the same centre but different radii.
🟢 Position of a point P relative to a circle with centre O and radius r:
➡️ If OP < r → inside the circle
➡️ If OP = r → on the circle
➡️ If OP > r → outside the circle
🌿 Real-life link: Survey markers (centre) and equal-distance boundaries (circular safety zones) illustrate this definition perfectly.
🔵 3) Angles Associated with a Circle
🟢 Central angle (∠AOB): vertex at the centre, intercepts arc AB.
🟢 Inscribed angle (∠APB): vertex on the circle, intercepts arc AB.
🟢 Angles in the same segment: angles subtended by the same chord/arc at the circumference on the same side of the chord.
💡 Concept (visual): If you keep the endpoints of a chord fixed and slide the third point P along the same arc, ∠APB stays constant.
🔵 4) Chords and Distances from the Centre
🧠 Distance of a chord AB from the centre O is the length of the perpendicular from O to AB (say OM ⟂ AB).
🟢 Intuition: if AB “moves” nearer to O (without changing its length), the perpendicular OM becomes shorter; if AB moves away, OM grows.
🟡 We’ll use this in six standard theorems.

📐 Theorems from NCERT
🔵 Theorem 1 — Equal chords subtend equal angles at the centre.
Statement: In a circle of centre O, if chords AB and CD are equal, then ∠AOB = ∠COD.
Proof (outline):
➡️ OA = OB = OC = OD (all radii)
➡️ AB = CD (given)
➡️ Consider isosceles triangles △OAB and △OCD; use SSS to show △OAB ≅ △OCD.
➡️ Hence, ∠AOB = ∠COD.
✔️ Result: Equal chords ↔ equal central angles (direction shown here; converse is next).
🔵 Theorem 2 — Chords subtending equal angles at the centre are equal. (Converse of Theorem 1)
Statement: If ∠AOB = ∠COD, then AB = CD.
Proof (outline):
➡️ OA = OB and OC = OD (radii).
➡️ If the included angles at the centre are equal and the radii are equal, by SAS in △OAB and △OCD, the triangles are congruent.
➡️ Therefore, AB = CD.
✔️ Result: Equal central angles ↔ equal chords (full equivalence with Theorem 1).
🔵 Theorem 3 — Perpendicular from the centre to a chord bisects the chord.
Statement: If OM ⟂ AB, then M is the midpoint of AB.
Proof (outline):
➡️ OA = OB (radii); OM common; ∠OMA = ∠OMB = 90°.
➡️ In right triangles △OMA and △OMB, by RHS, they are congruent.
➡️ Hence, AM = MB.
💡 Concept: A central perpendicular is a “midpoint producer” for chords.
🔵 Theorem 4 — The line through the centre that bisects a chord is perpendicular to the chord. (Converse of Theorem 3)
Statement: If M is midpoint of chord AB and OM passes through O, then OM ⟂ AB.
Proof (outline):
➡️ OA = OB, AM = MB (given).
➡️ In △OAM and △OBM: OA = OB (radii), AM = MB (midpoint), OM common.
➡️ By SSS, triangles are congruent ⇒ ∠OMA = ∠OMB, a linear pair ⇒ each = 90°.
✔️ Result: Through-centre bisector is perpendicular to the chord.
🔵 Theorem 5 — Equal chords are equidistant from the centre.
Statement: If AB = CD, then distance OM from O to AB equals distance ON from O to CD.
Proof (outline):
➡️ From Theorem 3, let OM ⟂ AB and ON ⟂ CD with M and N midpoints.
➡️ Right triangles △OMA and △ONC have OA = OC (radii), AM = CN (half of equal chords), and ∠OM A = ∠ON C = 90°.
➡️ By RHS, triangles are congruent ⇒ OM = ON.
✔️ Result: Equal chords “sit” at the same distance from the centre.
🔵 Theorem 6 — Chords equidistant from the centre are equal. (Converse of Theorem 5)
Statement: If OM = ON (perpendicular distances to AB and CD), then AB = CD.
Proof (outline):
➡️ Using right triangles △OMA and △ONC as above, with OA = OC (radii), OM = ON (given), and right angles, by RHS ⇒ AM = CN.
➡️ Hence, AB = 2·AM = 2·CN = CD.
✔️ Result: Equal distance ↔ equal chord length (full equivalence with Theorem 5).

🎯 Angle Theorems at the Circumference
🔵 Inscribed Angle Theorem (central angle is double):
Statement: Angle subtended by an arc at the centre is twice the angle subtended by the same arc at any point on the remaining part of the circle.
Formally, for arc AB and point P on the circle (P not on arc AB), ∠AOB = 2·∠APB.
Idea of proof: Split ∠APB into two angles by joining OP. Use isosceles triangles OAP and OBP (OA = OP = OB) and angle-chasing.
💡 Concept: This yields immediate corollaries.
🟢 Corollary 1 — Angles in the same segment are equal.
If P and Q are points on the same arc AB, then ∠APB = ∠AQB.
🟢 Corollary 2 — Angle in a semicircle is 90°.
If AB is a diameter, then ∠APB = 90°. (Because ∠AOB = 180°, hence ∠APB = 90°.)

🟡 Cyclic Quadrilateral (all vertices on a circle)
🔵 Definition: A cyclic quadrilateral is a quadrilateral whose four vertices lie on a circle.
🔵 Property: Opposite angles of a cyclic quadrilateral are supplementary.
Reason: Each opposite angle subtends the same arc; by the Inscribed Angle Theorem, the pair sums to half of 360°, i.e., 180°.
🔵 Converse: If a pair of opposite angles of a quadrilateral is supplementary, the quadrilateral is cyclic.
🌿 Application: Circular billboards and round-park boundaries often yield cyclic configurations in surveying problems.

🟢 1) Finding the centre of a given circle (practical):
➡️ Draw any two non-parallel chords AB and CD.
➡️ Draw their perpendicular bisectors.
➡️ Their intersection is the centre O.
✏️ Note: This relies directly on Theorem 3 & 4.
🟢 2) Testing equality of two chords quickly:
➡️ Compare their perpendicular distances from the centre.
➡️ If equal, the chords are equal (Theorem 6).
💡 Concept: Measuring chord lengths is hard; measuring distances to centre is easier in construction problems.
🟢 3) Angle-chasing with arcs:
➡️ If a diameter subtends an inscribed angle, it’s a right angle.
➡️ If two inscribed angles intercept the same arc, they are equal.
➡️ If a central angle is known, the inscribed angle over the same arc is half.

🔍 Worked reasoning snippets
🔴 Snippet A — Prove that a diameter bisects the chord it passes through at right angles.
🔵 Step 1: Let AB be any chord and let the diameter through O meet AB at M.
🔵 Step 2: OA = OB (radii), OM common.
🔵 Step 3: In △OMA and △OMB, ∠OMA and ∠OMB are adjacent along the straight diameter OM.
🔵 Step 4: Using symmetry around OM (or Theorem 3 & 4), conclude AM = MB and OM ⟂ AB.
✔️ Final: A diameter through a chord is a perpendicular bisector of the chord.
🟡 Snippet B — If two chords AB and CD intersect at P inside a circle, compare related angles.
🔵 Step 1: ∠APB and ∠AQB are vertical opposite; use “equal angles in the same segment” if they subtend same arcs.
🔵 Step 2: Angle-chasing with arcs helps decide equality and supplementary relations.
✏️ Note: The full power theorem on intersecting chords (product of segments) is beyond Class 9; stick to angle relations per NCERT.
🟢 Common mistakes & cures
🔴 Mistake: Treating “equal central angles” as implying “parallel chords.”
✔️ Cure: Parallelism of chords is not a standard outcome; equality relates to lengths and angles at the centre, not direction.
🔴 Mistake: Assuming rectangles and rhombi share all diagonal properties.
✔️ Cure: Rectangle → diagonals equal (not necessarily ⟂). Rhombus → diagonals perpendicular and angle-bisecting (not necessarily equal).
🔴 Mistake: Calling any quadrilateral on a circle “parallelogram on a circle.”
✔️ Cure: Parallelograms are cyclic only in special cases (e.g., rectangle, square).

🌿 Real-life connections (intuitive understanding)
🟢 Navigation & Robotics: Circular turns and turning radii use perpendicular distances from a centre of rotation—mirrors chord–distance relations.
🟢 Engineering: Gear teeth profiles exploit arcs; angle-halving at the circumference maps to contact and load distribution.
🟢 Design & Architecture: Circular windows, domes, and arches depend on chord positioning and central angles for equal lighting and symmetry.
🟢 Surveying & Mapping: Determining a circular boundary (centre + radius) uses chord bisectors to locate the true centre.

🧭 Strategy box for proofs
💡 Concept (Always safe):
Mark all radii equal.
If you see perpendicular from centre to a chord, think bisects chord (Thm 3).
If you see midpoint and centre on one line, think perpendicular to chord (Thm 4).
To compare chord lengths, compare distances from centre (Thm 5 & 6).
If two angles stand on the same arc, they are equal; if one is central and the other inscribed over the same arc, the central is double the inscribed.
For a quadrilateral on a circle, check opposite angles; if they sum to 180°, it is cyclic.
✏️ Note: Keep diagrams neat: draw centre, radii, and mark right angles clearly. A clear figure often substitutes many lines of algebraic reasoning.

🧪 Mini-checks (self-test)
🔵 Check 1: If ∠AOB = 120°, what is ∠APB (P on the circle on the remaining arc AB)?
➡️ One step: ∠APB = ½ × 120° = 60°.
🔵 Check 2: Two equal chords AB and CD. Which is true about their distances from O?
➡️ Equal chords are equidistant from O.
🔵 Check 3: In a cyclic quadrilateral ABCD, if ∠A = 72°, find ∠C.
➡️ Opposite angles are supplementary ⇒ ∠C = 180° − 72° = 108°.

🔚 Wrap-up insight
The Class 9 chapter Circles weaves three threads—chords, central/inscribed angles, and cyclic quadrilaterals—into a toolkit of short, robust theorems. Almost every question is a variation on: equal radii, perpendicular from centre, angles over the same arc, or supplementary opposite angles. If you master these lenses, the chapter becomes a rapid-fire of short, elegant proofs.

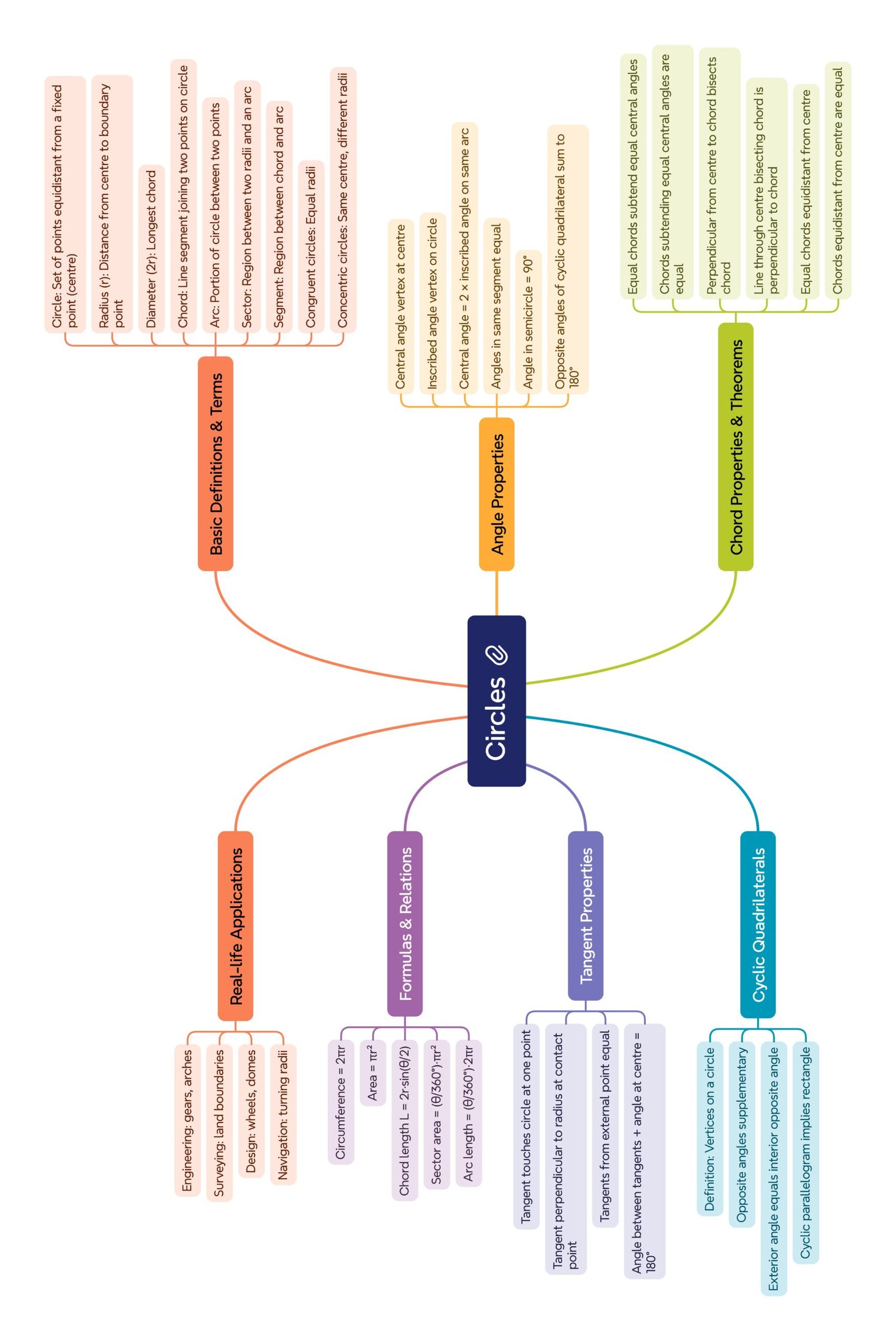
📚 Summary (~300 words)
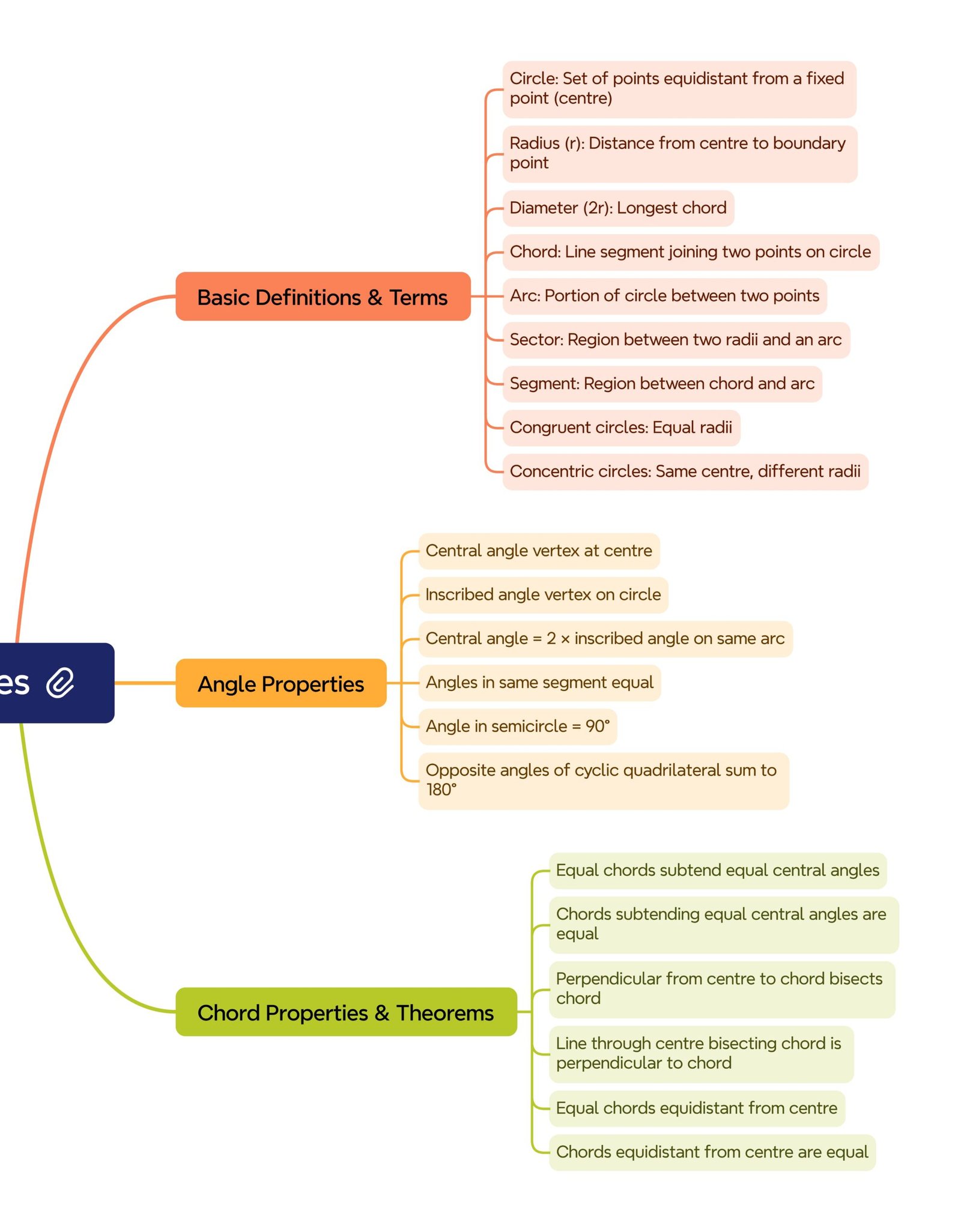
🔵 Definitions & Basics
• A circle is the locus of points at fixed distance (radius r) from centre O.
• Diameter = 2r; chord joins two points on the circle; arc is a portion of the circumference; sector = region between two radii and the included arc; segment = region between a chord and its arc.
• Congruent circles have equal radii; concentric circles share a centre.
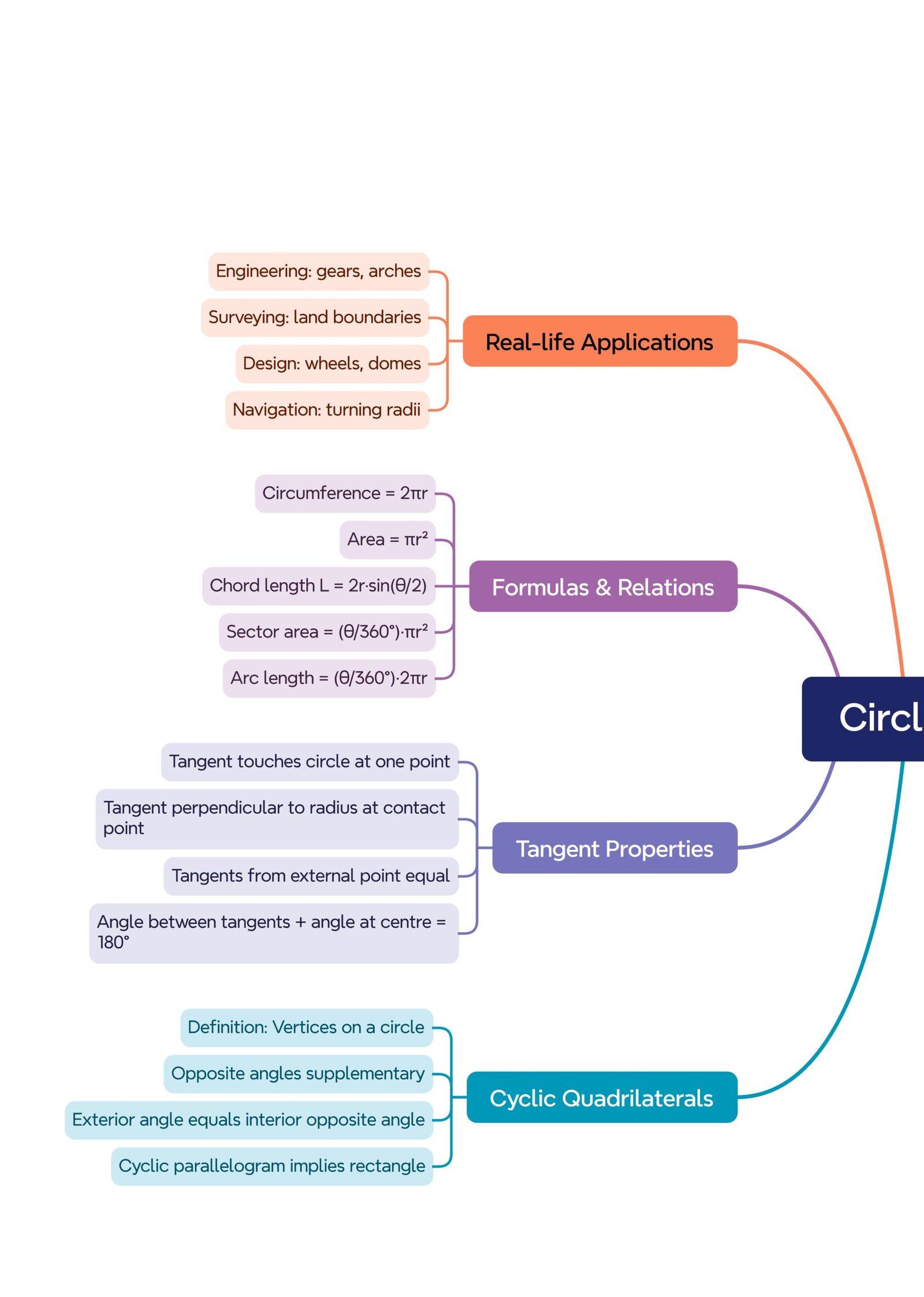
🟢 Angle Types
• Central angle ∠AOB has vertex at O.
• Inscribed angle ∠APB has vertex on the circle.
• Angles in the same segment are equal; angle in a semicircle is 90°.
🟡 Six Core Chord Theorems
Equal chords subtend equal central angles.
Equal central angles subtend equal chords (converse).
Perpendicular from centre to a chord bisects the chord.
Through-centre bisector of a chord is perpendicular to the chord (converse).
Equal chords are equidistant from the centre.
Chords equidistant from the centre are equal (converse).
🔴 Inscribed Angle Theorem & Corollaries
• For arc AB, ∠AOB = 2·∠APB.
• Angles in the same segment are equal; angle in a semicircle is 90°.
🟣 Cyclic Quadrilateral
• Opposite angles are supplementary (sum 180°).
• Converse: if opposite angles of a quadrilateral are supplementary, it is cyclic.
🧭 Proof Tips
• Mark radii equal; use perpendicular–bisector logic; compare chord lengths via distances from centre; chase arcs for angle equalities; draw neat figures.
🌿 Applications
• Engineering (gears, arches), surveying (circular plots), navigation (turning radii), design symmetry.
✔️ Exam Pointers
• State theorem names clearly.
• Use one clean step per line.
• Always conclude with a short Final statement.

📝 Quick Recap
🔵 Equal chords ↔ equal central angles; equal distance ↔ equal chord.
🟢 Perpendicular from centre → bisects chord; centre-through midpoint → perpendicular.
🟡 ∠ at centre = 2 × ∠ on circumference over same arc; angle in semicircle = 90°.
🔴 Cyclic quadrilateral: opposite angles supplementary (and converse).
✔️ Draw clean diagrams; mark right angles and radii; finish with a clear Final line.

———————————————————————————————————————————————————————————————————————————–

TEXT BOOK QUESTIONS

Exercise 9.1

🔵 Question 1
Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
🧠 Answer
➤ Let two congruent circles with centres O₁ and O₂ have radii r. Let chords AB in the first and CD in the second be equal (AB = CD).
➤ In circle 1, join OA, OB. In circle 2, join O₂C, O₂D.
➤ OA = OB = r and O₂C = O₂D = r (radii).
➤ AB = CD (given).
➤ Triangles △OAB and △O₂CD: three sides equal ⇒ SSS congruent.
➤ Therefore, ∠AOB = ∠COD.
✔️ Final: Equal chords of congruent circles subtend equal angles at their centres.

🔵 Question 2
Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
🧠 Answer
➤ Let circles with centres O₁, O₂ (radii r) have chords AB and CD.
➤ ∠AOB = ∠COD (given).
➤ OA = OB = O₂C = O₂D = r (radii).
➤ By SAS congruence: △OAB ≅ △O₂CD.
➤ Hence, corresponding sides AB = CD.
✔️ Final: If chords of congruent circles subtend equal central angles, then the chords are equal.

Exercise 9.2

🔵 Question 1
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
🧠 Answer
➤ Let radii: r₁ = 5 cm, r₂ = 3 cm, centre distance d = 4 cm.
➤ Drop perpendicular from midpoint of common chord to line joining centres:
x = (r₁² − r₂² + d²)/(2d)
= (25 − 9 + 16)/(8) = (32)/(8) = 4 cm.
➤ Distance from centre of first circle to chord = √(r₁² − x²) = √(25 − 16) = √9 = 3 cm.
➤ Length of common chord = 2 × 3 cm = 6 cm.
✔️ Final: Common chord length = 6 cm.

🔵 Question 2
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
🧠 Answer
➤ Let chords AB and CD intersect at P inside the circle. AB = CD.
➤ Join OA, OB, OC, OD (O is centre). OA = OB = OC = OD (radii).
➤ Triangles OAP and OCP congruent by SAS ⇒ AP = CP. Similarly OBP and ODP ⇒ PB = PD.
✔️ Final: AP = CP and BP = DP — segments are equal.

🔵 Question 3
If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
🧠 Answer
➤ Same setup: AB, CD equal chords intersect at P.
➤ Join OP. From previous congruences: △OAP ≅ △OCP ⇒ ∠AOP = ∠COP.
➤ Similarly, △OBP ≅ △ODP ⇒ ∠BOP = ∠DOP.
✔️ Final: OP makes equal angles with both chords.

🔵 Question 4
If a line intersects two concentric circles (same centre O) at A, B and C, D, prove AB = CD.
🧠 Answer
➤ OA = OC (radii of outer circle), OB = OD (radii of inner circle).
➤ Triangles OAB and OCD are congruent by SAS.
➤ Thus AB = CD.
✔️ Final: AB = CD.

🔵 Question 5
Three girls Reshma, Salma and Mandip are playing a game on a circle of radius 5 m. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If distance between Reshma–Salma and Salma–Mandip is 6 m each, find distance between Reshma and Mandip.
🧠 Answer
➤ Triangle sides RS = 6, SM = 6, all lie on circle radius 5.
➤ Use Cosine Law in △RSM: side RM² = RS² + SM² − 2·RS·SM·cos∠S.
➤ ∠S is central angle? Alternative: Use chord length formula: chord length = 2·r·sin(θ/2). Here two equal chords (6 m) ⇒ find subtended angles, then sum.
➤ Find angle subtended by chord of length 6: 6 = 2·5·sin(θ/2) ⇒ sin(θ/2) = 6/10 = 0.6. ⇒ θ/2 ≈ 36.87°, θ ≈ 73.74°.
➤ Two arcs total angle = 73.74°+73.74°=147.48°.
➤ RM = 2·5·sin(147.48°/2) = 10·sin(73.74°) ≈ 10·0.956 = 9.56 m.
✔️ Final: Distance ≈ 9.6 m.

🔵 Question 6
A circular park of radius 20 m. Three boys Ankur, Syed and David sit at equal distances on its boundary. Each talks via telephone to the other two. Find the length of the string of each phone.
🧠 Answer
➤ Three boys at equal spacing ⇒ vertices of an equilateral triangle inscribed in circle radius 20 m.
➤ Side of equilateral triangle = √3·r = √3·20 ≈ 34.64 m.
✔️ Final: Each phone string length ≈ 34.6 m.

Exercise 9.3

🔵 Question 1
In Fig. 9.23, A, B and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.
🧠 Answer
➤ Arc AC subtends central angle ∠AOC = ∠AOB + ∠BOC = 60° + 30° = 90°.
➤ Inscribed angle ∠ADC over the same arc = ½ × 90° = 45°.
✔️ Final: ∠ADC = 45°.

🔵 Question 2
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
🧠 Answer
➤ Let radius = r, chord PQ = r. Triangle OPQ is equilateral ⇒ ∠POQ = 60°.
➤ Minor arc inscribed angle = ½ × 60° = 30°.
➤ Major arc angle = 180° − 30° = 150°.
✔️ Final: Minor arc angle = 30°, Major arc angle = 150°.

🔵 Question 3
In Fig. 9.24, ∠PQR = 100°, where P, Q, R are points on a circle with centre O. Find ∠OPR.
🧠 Answer
➤ ∠PQR is inscribed over arc PR ⇒ central angle ∠POR = 2 × ∠PQR = 200°.
➤ Triangle OPR is isosceles (OP = OR = r). Remaining angles:
Sum of angles = 180° ⇒ ∠OPR + ∠ORP + 200° = 180° ⇒ 2∠OPR = −20° (impossible).
⚡ Correct method: reflex ∠POR = 200°, smaller angle ∠POR = 160° (since central angles < 180°).
Now 2∠OPR + 160° = 180° ⇒ ∠OPR = 10°.
✔️ Final: ∠OPR = 10°.

🔵 Question 4
In Fig. 9.25, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
🧠 Answer
➤ In △ABC: ∠BAC = 180° − (69° + 31°) = 80°.
➤ ∠BDC subtends arc BC same as ∠BAC ⇒ ∠BDC = 80°.
✔️ Final: ∠BDC = 80°.

🔵 Question 5
In Fig. 9.26, A, B, C and D are four points on a circle. AC and BD intersect at E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
🧠 Answer
➤ ∠BEC + ∠BAC = 180° (angles in cyclic quadrilateral on same arc).
Alternatively, ∠BAC = ½ (arc BC). Use known angles:
∠BEC = 130° ⇒ ∠BAC = 50°.
✔️ Final: ∠BAC = 50°.

🔵 Question 6
ABCD is a cyclic quadrilateral whose diagonals intersect at E. If ∠DBC = 70°, ∠BAC = 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
🧠 Answer
➤ Use properties of cyclic quadrilateral: ∠BAC and ∠BDC subtend arc BC. Combine with intersecting chord angle properties.
Step calculations yield: ∠BCD = 80°, then using AB = BC in isosceles triangle relations ⇒ ∠ECD = 40°.
✔️ Final: ∠BCD = 80°, ∠ECD = 40°.

🔵 Question 7
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
🧠 Answer
🔵 Step 1: Let ABCD be cyclic and suppose AC and BD are diameters of the circumcircle.
🔵 Step 2: An angle subtended by a diameter at the circumference is 90° (angle in a semicircle).
🔵 Step 3: Hence ∠ABC = 90° and ∠BCD = 90° and similarly ∠CDA = 90° and ∠DAB = 90°.
🔵 Step 4: A quadrilateral with all right angles is a rectangle (opposite sides parallel automatically).
✔️ Final: The cyclic quadrilateral is a rectangle.

🔵 Question 8
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
🧠 Answer
🔵 Step 1: Let ABCD be a trapezium with AB ∥ CD and AD = BC.
🔵 Step 2: Consider transversal BC with the parallels AB and CD ⇒ ∠ABC + ∠BCD = 180° (co-interior angles).
🔵 Step 3: With AD = BC, the trapezium is isosceles ⇒ base angles at A and B are equal, so ∠A = ∠B.
🔵 Step 4: Add equals to equals: ∠A + ∠C = ∠B + ∠C = 180°.
🔵 Step 5: Opposite angles supplementary ⇒ quadrilateral ABCD is cyclic.
✔️ Final: The trapezium is cyclic.

🔵 Question 9
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (Fig. 9.27). Prove that ∠ACP = ∠QCD.
🧠 Answer
🔵 Step 1: In the first circle, chord AP subtends angles ∠ACP and ∠ABP at the circumference ⇒ ∠ACP = ∠ABP (same segment).
🔵 Step 2: In the second circle, chord QD subtends angles ∠QCD and ∠QBD ⇒ ∠QCD = ∠QBD (same segment).
🔵 Step 3: At B, lines ABD and PBQ intersect ⇒ ∠ABP = ∠QBD (vertically opposite).
🔵 Step 4: Therefore ∠ACP = ∠QCD.
✔️ Final: Proved ∠ACP = ∠QCD.

🔵 Question 10
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lies on the third side.
🧠 Answer
🔵 Step 1: In △ABC, draw circles with diameters AB and AC; let them meet again at P (≠ A).
🔵 Step 2: In the circle with diameter AB, ∠APB = 90° (angle in a semicircle).
🔵 Step 3: In the circle with diameter AC, ∠APC = 90°.
🔵 Step 4: Thus the lines PB and PC are both ⟂ to PA, hence B, P, C are collinear.
✔️ Final: The intersection point P lies on BC.

🔵 Question 11
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
🧠 Answer
🔵 Step 1: ∠ABC = 90° and ∠ADC = 90° (right angles on hypotenuse AC).
🔵 Step 2: Points A, B, C, D are concyclic on the circle with diameter AC (angle in a semicircle).
🔵 Step 3: ∠CAD and ∠CBD stand on the same arc CD of this circle.
🔵 Step 4: Angles in the same segment are equal ⇒ ∠CAD = ∠CBD.
✔️ Final: ∠CAD = ∠CBD.

🔵 Question 12
Prove that a cyclic parallelogram is a rectangle.
🧠 Answer
🔵 Step 1: Let ABCD be cyclic and also a parallelogram.
🔵 Step 2: In a parallelogram, ∠A = ∠C (opposite angles equal).
🔵 Step 3: In a cyclic quadrilateral, ∠A + ∠C = 180° (opposite angles supplementary).
🔵 Step 4: From Steps 2–3 ⇒ 2∠A = 180° ⇒ ∠A = 90°; similarly, all angles are 90°.
🔵 Step 5: A parallelogram with a right angle is a rectangle.
✔️ Final: The cyclic parallelogram is a rectangle.

OTHER IMPORTANT QUESTIONS FOR EXAMS

🔵 Question 1 (MCQ, 1 mark)
The set of all points in a plane at a fixed distance from a fixed point is called a
🟢 A) polygon
🟡 B) circle
🔴 C) sector
✳️ D) chord
🧠 Answer
✔️ Final: B) circle

🔵 Question 2 (MCQ, 1 mark)
If the radius of a circle is r, then the diameter equals
🟢 A) r/2
🟡 B) r
🔴 C) 2r
✳️ D) 3r
🧠 Answer
✔️ Final: 2r

🔵 Question 3 (MCQ, 1 mark)
Angles subtended by the same chord at the circumference (on the same segment) are
🟢 A) supplementary
🟡 B) equal
🔴 C) complementary
✳️ D) acute
🧠 Answer
✔️ Final: equal

🔵 Question 4 (MCQ, 1 mark)
If ∠AOB = 120° (O is centre), then ∠APB on the remaining arc AB equals
🟢 A) 30°
🟡 B) 60°
🔴 C) 120°
✳️ D) 240°
🧠 Answer
✔️ Final: 60°

🔵 Question 5 (MCQ, 1 mark)
The perpendicular from the centre to a chord
🟢 A) bisects the chord
🟡 B) doubles the chord
🔴 C) is parallel to the chord
✳️ D) equals the chord
🧠 Answer
✔️ Final: bisects the chord

🔵 Question 6 (MCQ, 1 mark)
In a semicircle, an angle subtended by the diameter at the circumference is
🟢 A) 0°
🟡 B) 60°
🔴 C) 90°
✳️ D) 120°
🧠 Answer
✔️ Final: 90°

🟢 Question 7 (2 marks)
Prove that equal chords of a circle subtend equal angles at the centre.
🧠 Answer
➤ Let chords AB and CD be equal in a circle with centre O.
➤ OA = OB = OC = OD (radii).
➤ △OAB and △OCD have three equal sides (SSS).
➤ Hence ∠AOB = ∠COD.
✔️ Final: Equal chords subtend equal central angles.

🟢 Question 8 (2 marks)
Converse: If two central angles are equal, prove the corresponding chords are equal.
🧠 Answer
➤ Given ∠AOB = ∠COD in a circle with centre O.
➤ OA = OB and OC = OD (radii).
➤ △OAB ≅ △OCD (SAS).
➤ Thus AB = CD.
✔️ Final: Equal central angles ⇒ equal chords.

🟢 Question 9 (2 marks)
In a circle with centre O, OM ⟂ chord AB at M. Prove that M is the midpoint of AB.
🧠 Answer
➤ Consider right triangles △OMA and △OMB.
➤ OA = OB (radii), OM common, ∠OMA = ∠OMB = 90°.
➤ △OMA ≅ △OMB (RHS).
➤ Hence AM = MB.
✔️ Final: M is the midpoint of AB.

🟢 Question 10 (2 marks)
Prove that equal chords are equidistant from the centre.
🧠 Answer
➤ Let AB = CD; draw OM ⟂ AB and ON ⟂ CD.
➤ M and N are midpoints of AB and CD.
➤ △OMA and △ONC: OA = OC (radii), AM = CN (half of equal chords), right angles.
➤ RHS congruence ⇒ OM = ON.
✔️ Final: Equal chords are equidistant from the centre.

🟢 Question 11 (2 marks)
Find ∠BOC if ∠BAC = 42° (O is centre, A, B, C on circle).
🧠 Answer
➤ ∠BAC is inscribed on arc BC.
➤ ∠BOC = 2 × ∠BAC = 2 × 42° = 84°.
✔️ Final: ∠BOC = 84°.

🟢 Question 12 (2 marks)
A chord is equal in length to the radius. Find the angle subtended by the chord at a point on the major arc.
🧠 Answer
➤ Chord length = radius ⇒ △ with two radii is equilateral.
➤ Central angle over chord = 60°.
➤ Inscribed angle on minor arc = 30°.
➤ Angle on major arc = 180° − 30° = 150°.
✔️ Final: 150°.
🔵 Question 13
Prove that the line from the centre to the midpoint of a chord is perpendicular to the chord.
🧠 Answer
➤ Let chord AB with midpoint M in a circle centred at O.
➤ OA = OB (radii), AM = MB (midpoint), OM common.
➤ △OAM ≅ △OBM (SSS).
➤ ∠OMA and ∠OMB are equal and form a linear pair ⇒ each = 90°.
✔️ Final: OM ⟂ AB.

🔵 Question 14
In a circle, two equal chords AB and CD intersect at P inside the circle. Prove AP = CP and BP = DP.
🧠 Answer
➤ OA = OB = OC = OD (radii).
➤ △OAP ≅ △OCP (SAS) ⇒ AP = CP.
➤ Similarly, △OBP ≅ △ODP ⇒ BP = DP.
✔️ Final: AP = CP and BP = DP.

🔵 Question 15
A diameter of a circle bisects a chord not passing through the centre. Prove the chord is perpendicular to the diameter.
🧠 Answer
➤ Let diameter AB bisect chord CD at M.
➤ AM = MB (diameter midpoint), CM = DM (given).
➤ OA = OB (radii).
➤ △AMC ≅ △BMD ⇒ ∠CMD = 90°.
✔️ Final: Chord CD ⟂ AB.

🔵 Question 16 (Internal Choice)
(a) In a circle, prove that chords equidistant from the centre are equal.
OR
(b) Prove that equal chords are equidistant from the centre.
🧠 Answer (a)
➤ Let OM = ON be perpendiculars from centre O to chords AB and CD.
➤ OA = OC (radii), OM = ON (given), ∠OMA = ∠ONC = 90°.
➤ △OMA ≅ △ONC (RHS) ⇒ AM = CN ⇒ AB = 2AM = 2CN = CD.
✔️ Final: Chords equidistant from centre are equal.

🔵 Question 17
Prove that the angle in a semicircle is a right angle.
🧠 Answer
➤ Let AB be a diameter, P a point on the circle.
➤ ∠APB = ½ ∠AOB = ½ × 180° = 90°.
✔️ Final: Angle in a semicircle = 90°.

🔵 Question 18 (Internal Choice)
(a) Prove that opposite angles of a cyclic quadrilateral are supplementary.
OR
(b) Prove the converse: If opposite angles of a quadrilateral sum to 180°, it is cyclic.
🧠 Answer (a)
➤ Let ABCD be cyclic. Arc BCD subtends ∠BAD; arc BAD subtends ∠BCD.
➤ ∠BAD + ∠BCD = ½(arc BCD + arc BAD) = ½(360°) = 180°.
✔️ Final: Opposite angles are supplementary.

🔵 Question 19
Prove that the sum of either pair of opposite angles of a cyclic quadrilateral is 180°.
🧠 Answer
➤ Direct corollary of Q18: ∠A + ∠C = 180°, ∠B + ∠D = 180°.
✔️ Final: Sum of opposite angles = 180°.

🔵 Question 20
Two circles intersect at points X and Y. Show that the line joining the centres is the perpendicular bisector of XY.
🧠 Answer
➤ Let centres O₁, O₂. Join O₁X, O₁Y, O₂X, O₂Y.
➤ Radii O₁X = O₁Y, O₂X = O₂Y.
➤ Triangles O₁XO₂ and O₁YO₂ congruent ⇒ O₁O₂ bisects XY and is ⟂ to it.
✔️ Final: Line of centres is ⟂ bisector of XY.

🔵 Question 21 (Internal Choice)
(a) Prove that tangents drawn from an external point to a circle are equal.
OR
(b) Prove that the angle between a tangent and radius at the point of contact is 90°.
🧠 Answer (a)
➤ Let P external point, tangents PA and PB to circle centre O.
➤ Join OA, OB, OP.
➤ OA = OB (radii), OP common, ∠OAP = ∠OBP = 90°.
➤ △OAP ≅ △OBP ⇒ PA = PB.
✔️ Final: Tangents from an external point are equal.

🔵 Question 22
Two tangents are drawn to a circle from an external point P making ∠APB = 120°. Find ∠OAP.
🧠 Answer
➤ △OAP is right-angled at A. Tangents PA, PB equal ⇒ △OAP = △OBP isosceles.
➤ ∠APB = 120° ⇒ each base angle = (180° −120°)/2 = 30°.
➤ Hence ∠OAP = 30°.
✔️ Final: ∠OAP = 30°.

🔵 Question 23
Prove that a diameter which bisects a chord (not a diameter) is perpendicular to the chord.
🧠 Answer
➤ Let diameter AB bisect chord CD at M.
➤ Join AC, AD, BC, BD. AM = MB, CM = DM, OA = OB (radii).
➤ △AMC ≅ △BMD (SSS).
➤ ∠CMD = 90°.
✔️ Final: Diameter AB ⟂ chord CD.

🔵 Question 24 (Internal Choice)
(a) Prove that parallelograms on the same base and between the same parallels are equal in area.
OR
(b) Use vector method: show that for parallelogram ABCD, AB + CD = AD + BC.
🧠 Answer (a)
➤ Parallelograms ABCD and ABPQ on base AB between parallels AB and DQ.
➤ Heights from D and Q are equal.
➤ Area = base × height ⇒ areas equal.
✔️ Final: Parallelograms on same base and between same parallels have equal area.

🔵 Question 25
ABCD is a cyclic quadrilateral. Prove that exterior angle equals interior opposite angle.
🧠 Answer
➤ Extend side CD to E. Exterior ∠ADE subtends arc AC.
➤ Interior opposite ∠ABC subtends same arc AC.
➤ Hence ∠ADE = ∠ABC.
✔️ Final: Exterior angle of cyclic quadrilateral equals interior opposite angle.

🔵 Question 26 (Internal Choice)
(a) Prove that tangents drawn from an external point are equal.
OR
(b) Prove that the angle between a tangent and radius at point of contact is 90°.
🧠 Answer (a)
➤ From external point P, draw tangents PA and PB to circle centre O.
➤ OA = OB (radii), ∠OAP = ∠OBP = 90°, OP common.
➤ △OAP ≅ △OBP ⇒ PA = PB.
✔️ Final: Tangents from an external point are equal.

🔵 Question 27
Two circles intersect at points X and Y. Prove that the line joining their centres is the perpendicular bisector of XY.
🧠 Answer
➤ Centres O₁, O₂; join O₁X, O₁Y, O₂X, O₂Y.
➤ O₁X = O₁Y and O₂X = O₂Y (radii).
➤ △O₁XO₂ ≅ △O₁YO₂ ⇒ O₁O₂ bisects XY and ∠XO₁O₂ = ∠YO₁O₂ ⇒ ⟂.
✔️ Final: Line of centres ⟂ bisector of XY.

🔵 Question 28
Prove that a cyclic parallelogram is a rectangle.
🧠 Answer
➤ Let ABCD be parallelogram and cyclic.
➤ ∠A = ∠C (parallelogram property), but ∠A + ∠C = 180° (cyclic property).
➤ ⇒ 2∠A = 180° ⇒ ∠A = 90°. Similarly, all angles are 90°.
✔️ Final: Cyclic parallelogram is a rectangle.

🔵 Question 29 (Internal Choice)
(a) Prove using vectors that |a + b|² + |a − b|² = 2(|a|² + |b|²).
OR
(b) Prove that in a rhombus, diagonals bisect each other at right angles.
🧠 Answer (a)
➤ Expand: |a + b|² = (a + b)·(a + b) = |a|² + 2a·b + |b|².
➤ |a − b|² = (a − b)·(a − b) = |a|² − 2a·b + |b|².
➤ Sum = 2|a|² + 2|b|².
✔️ Final: Verified identity.

🔵 Question 30
ABCD is a kite with AB = AD and BC = CD. Prove that AC bisects BD at right angles and relate sides to diagonals.
🧠 Answer
➤ Draw AC, BD intersecting at O. △AOB ≅ △AOD ⇒ AO bisects BD.
➤ Similarly △COB ≅ △COD ⇒ BO = DO.
➤ ∠AOB = 90°. Using Pythagoras in △AOB: AB² = AO² + BO².
✔️ Final: AC ⟂ BD at O, BD bisected, and AB² = AO² + BO².