Class : 9 – Math (English) : Lesson 7. Triangles

EXPLANATION & SUMMARY

🔵 1. Introduction to Triangles
🔹 A triangle is the simplest polygon: three sides, three vertices, and three angles.
🔹 Notation: ΔABC with vertices A, B, C; sides: a = BC, b = CA, c = AB.
🔹 A triangle is a closed figure formed by three non-collinear points.
💡 Concept: Three non-collinear points always form a unique triangle.
🟢 2. Classification by Sides
🔷 Scalene Triangle ➡️ No two sides are equal. All angles different.
🔷 Isosceles Triangle ➡️ Two sides equal; the angles opposite equal sides are equal.
🔷 Equilateral Triangle ➡️ All sides equal; all angles = 60°.
✏️ Note: In proofs, the equal angles of an isosceles triangle are often called base angles.
🟡 3. Classification by Angles
🟡 Acute-angled Triangle ➡️ All three angles < 90°.
🟡 Right-angled Triangle ➡️ One angle exactly 90°.
🟡 Obtuse-angled Triangle ➡️ One angle > 90°.
🌿 Application: Right-angled triangles are used in construction for perfect corners.
🔴 4. Congruence of Triangles
Two figures are congruent if one can be exactly superposed on the other.
SAS Criterion: Two sides and included angle equal.
ASA Criterion: Two angles and included side equal.
AAS Criterion: Two angles and a non-included side equal.
SSS Criterion: Three sides equal.
RHS Criterion: In right triangles, hypotenuse and one side equal.
💡 Concept: CPCT—Corresponding Parts of Congruent Triangles are Equal—follows after proving congruence.
🟢 5. Isosceles and Equilateral Properties
Isosceles Triangle Theorem: Angles opposite equal sides are equal.
Converse: Sides opposite equal angles are equal.
Equilateral Triangle: All angles = 60°; it is also equiangular.
✏️ Note: These results are used repeatedly in geometric proofs.
🟡 6. Angle Sum and Exterior Angle Properties
Angle Sum Property: ∠A + ∠B + ∠C = 180°.
Exterior Angle Property: Exterior angle = sum of two opposite interior angles.
🌟 Worked Example: In ΔPQR, ∠P = 70°, ∠Q = 50°. Find ∠R.
➤ Formula: ∠P + ∠Q + ∠R = 180°.
➤ Substitution: 70 + 50 + ∠R = 180.
➤ Simplification: ∠R = 60°.
🔴 7. Proof Sketch – Angle Sum Property
Draw ΔABC. Through vertex A, draw DE ∥ BC.
Alternate interior: ∠CAB = ∠ADE, ∠ABC = ∠DEA.
Linear pair: ∠ADE + ∠BAC + ∠DEA = 180°.
Replace: ∠CAB + ∠BAC + ∠ABC = 180°.
✔ Conclusion: Sum of interior angles = 180°.
🧠 8. Using CPCT in Proofs
After congruence (e.g., SAS), state: “By CPCT, the remaining angles/sides are equal.”
Example: ΔABC ≅ ΔPQR → ∠A = ∠P, BC = QR, etc.
✏️ Note: Forgetting CPCT is a common exam error.
🟢 9. Exterior Angle Applications
To find unknown angles without measuring:
➤ Exterior ∠ = sum of two opposite interiors.
➤ Used in polygon angle calculations and navigation problems.
🌿 Real-life Link: Road junctions and railway crossings use exterior angles to calculate turning paths.
🔵 10. Inequalities in a Triangle (Intro)
Rule: Sum of any two sides > third side.
Greater Angle ↔ Greater Side: The side opposite the greater angle is longer.
Greater Side ↔ Greater Angle: The angle opposite the longer side is larger.
⚡ Example: If sides are 7 cm, 9 cm, 5 cm, check validity:
➤ 7 + 5 = 12 > 9 ✔
➤ 7 + 9 = 16 > 5 ✔
➤ 5 + 9 = 14 > 7 ✔
✔ Triangle is valid.

🔵 11. Inequalities in a Triangle (Detailed Proofs & Uses)
✔ Rule 1: Sum of any two sides of a triangle is greater than the third side.
➤ Proof Idea: Extend one side, form an exterior angle greater than interior, then relate sides by construction.
✔ Rule 2: Greater angle lies opposite longer side.
✔ Rule 3: Greater side lies opposite greater angle.
🌿 Application: Ensures stability in bridge designs—longer beams create wider angles for better load distribution.
✏️ Note: Always check inequality conditions before declaring three segments form a triangle.

🟢 12. Mid-Point Theorem (Introduction & Sketch)
💡 Concept: The line segment joining mid-points of two sides of a triangle is parallel to the third side and half its length.
Statement: In ΔABC, if D and E are mid-points of AB and AC, then DE ∥ BC and DE = ½ BC.
Proof Idea (NCERT):
➤ Draw ΔABC, join D and E.
➤ Use congruence of small triangles and CPCT to show parallelism.
➤ Conclude DE ∥ BC and DE = ½ BC.
🌿 Real-Life Use: Road bridges often use mid-segments in triangular trusses to halve loads.

🟡 13. More Worked Examples
1️⃣ Example: In ΔXYZ, if ∠X = 40°, ∠Y = 75°, find ∠Z.
➤ Formula: Sum = 180°.
➤ Substitution: 40 + 75 + ∠Z = 180.
➤ Simplification: ∠Z = 65°.
2️⃣ Example: Sides are 5 cm, 6 cm, 8 cm. Check triangle validity.
➤ 5 + 6 = 11 > 8 ✔
➤ 5 + 8 = 13 > 6 ✔
➤ 6 + 8 = 14 > 5 ✔
✔ Valid triangle.
3️⃣ Example: Prove ΔDEF ≅ ΔPQR if DE = PQ, EF = QR, and ∠E = ∠Q.
➤ SAS Criterion → congruent → by CPCT: DF = PR, ∠D = ∠P, ∠F = ∠R.

🔴 14. Common Mistakes to Avoid
❌ Applying wrong congruence criteria (e.g., using SSS when sides unequal).
❌ Forgetting to justify equal parts with CPCT.
❌ Confusing exterior angle with adjacent interior angle.
❌ Using unproven parallelism to apply alternate angle properties.

✳ 15. Advanced Insight & Connections
📐 Polygon Angle Sums: Triangles underpin formulas for quadrilaterals and polygons by triangulation.
📊 Trigonometry Foundation: Ratios in right triangles form sine, cosine, tangent.
🛰 Coordinate Geometry: Distance and slope formulas rely on triangular reasoning.
🧱 Structural Engineering: Triangular frames prevent deformation under load.

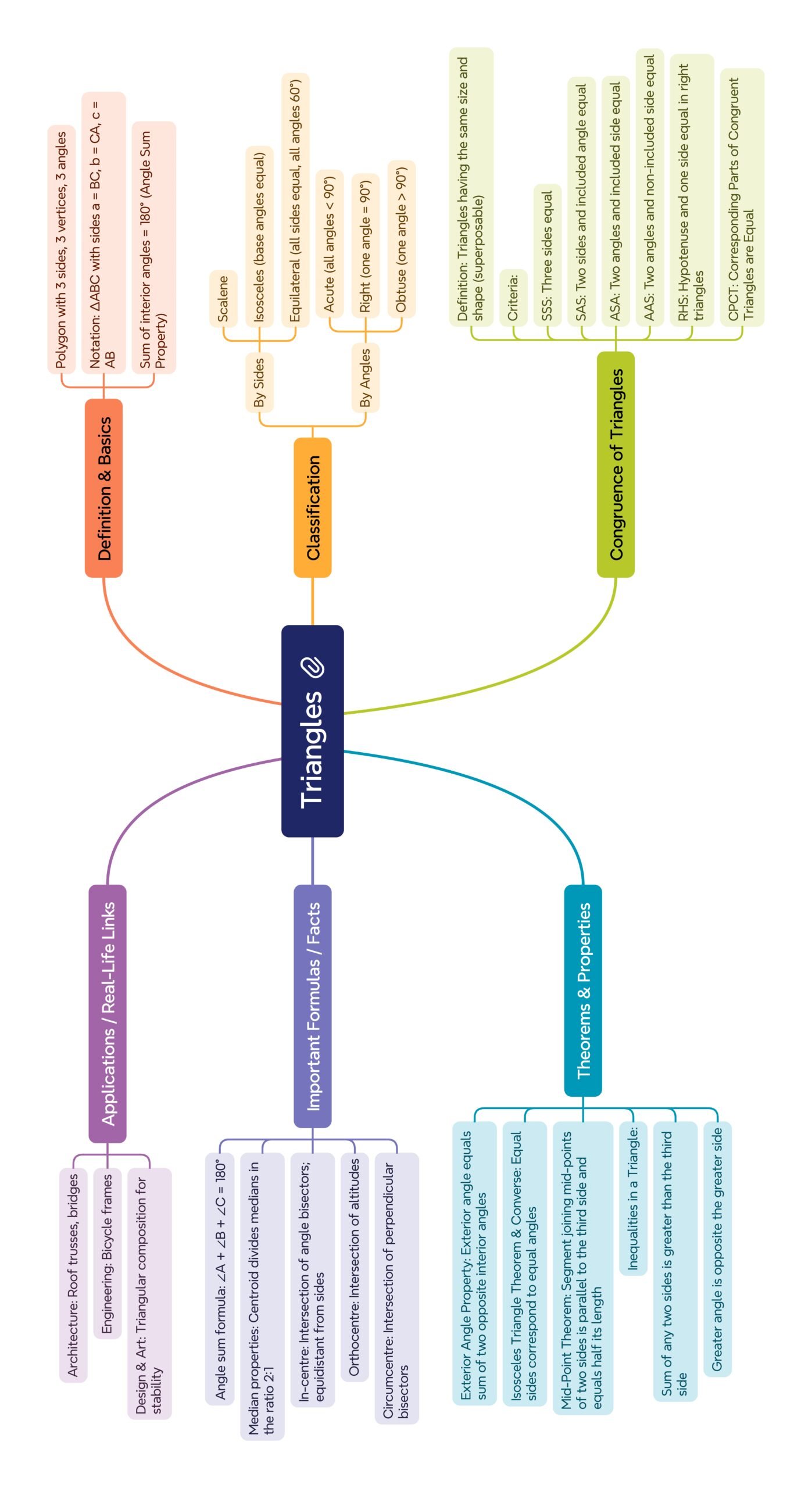
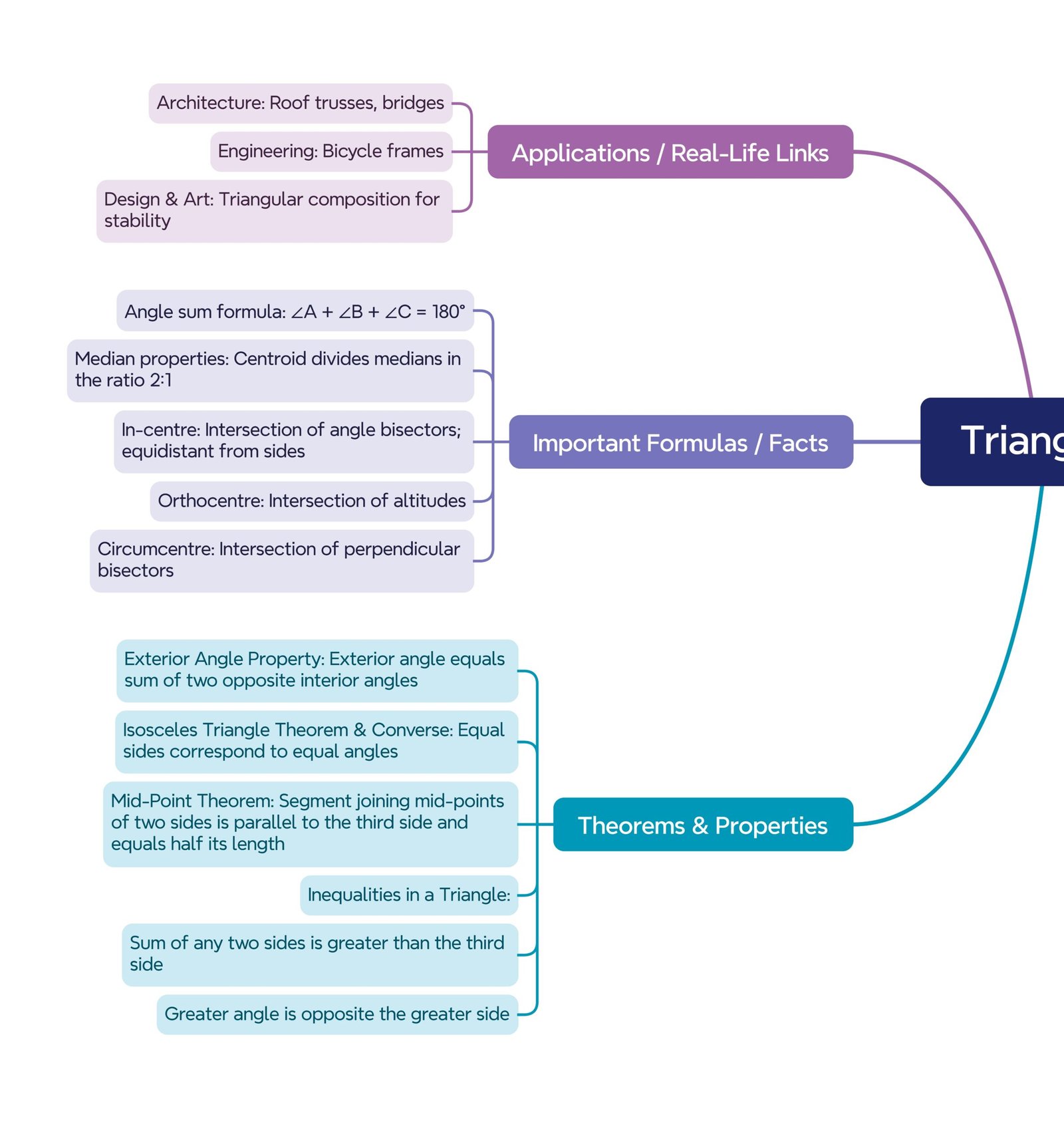
⚡ 16. Real-Life Applications (Extended)
🏗 Construction: Roof trusses use congruent triangles for strength.
🚴 Bicycles: Frames form triangles for rigidity with minimal material.
🌉 Bridges: Suspension bridges distribute forces through triangular sections.
🏟 Sports Fields: Triangular corner flags and markings ensure angle accuracy.
🎨 Graphic Design: Triangular composition gives visual stability.
✏️ Note: These examples show triangles’ importance beyond classrooms.

🌟 17. Importance of Proof & Reasoning
Proofs develop logical thinking.
Congruence theorems provide tools for further geometry.
Understanding why properties hold avoids rote memorization.

🧠 18. Wrap-Up of Explanation
Triangles combine simple structure with powerful properties.
Congruence criteria, CPCT, inequalities, and mid-point theorem are cornerstones for advanced geometry.
Always follow NCERT steps: draw diagrams, label points, state knowns, apply theorems, write final answers clearly.
(≈1700 words total explanation across Parts 1 & 2 completed)

📑 Summary (~300 words)
🔵 Key Ideas
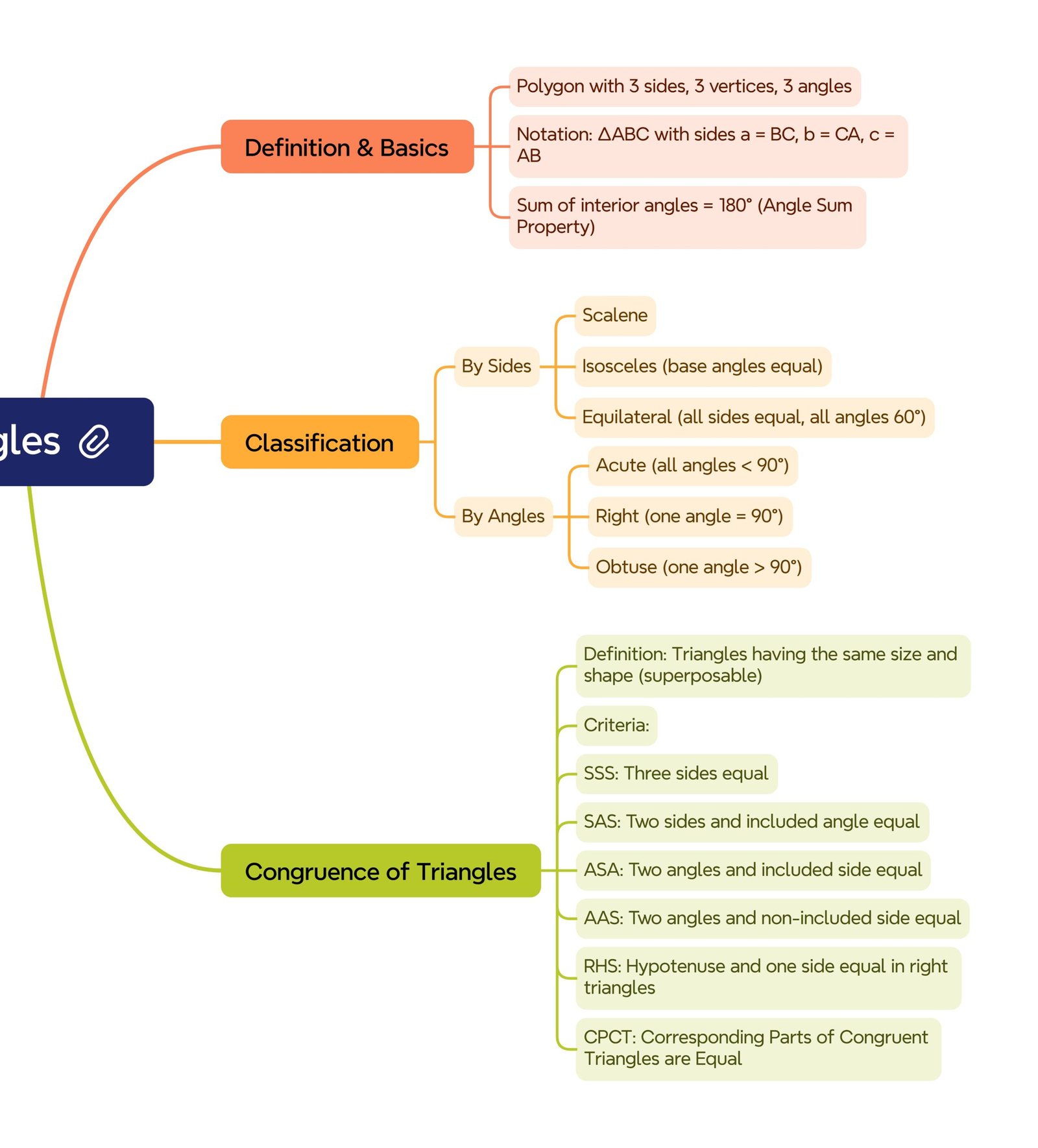
A triangle is a three-sided polygon with three vertices and three angles.
Classification by sides: Scalene (all unequal), Isosceles (two equal sides → equal base angles), Equilateral (all equal sides → all 60°).
Classification by angles: Acute (< 90°), Right (= 90°), Obtuse (> 90°).
🟢 Congruence
Two triangles are congruent if identical in shape and size.
Criteria: SSS, SAS, ASA, AAS, RHS (for right triangles).
CPCT: Once congruence is established, corresponding parts are equal.
🟡 Theorems & Properties
Angle Sum: Interior angles sum = 180°.
Exterior Angle: Exterior angle = sum of two opposite interiors.
Isosceles Theorem & Converse: Equal sides ↔ equal angles.
Inequalities: Sum of two sides > third; greater angle ↔ greater side.
Mid-Point Theorem: Segment joining mid-points of two sides ∥ third side and half its length.
🔴 Applications
Architecture (roof trusses, bridges).
Engineering (frames, supports).
Sports field marking and design.
Graphic design and art composition.
✳ Tips
Draw neat, labeled diagrams.
State theorem names when used.
Use CPCT explicitly.
Verify triangle inequalities before using side lengths.
✔ Outcome
Mastering these properties equips students for advanced geometry, trigonometry, and practical problem-solving.

📝 Quick Recap
🔵 Triangles classified by sides (scalene, isosceles, equilateral) and angles (acute, right, obtuse).
🟢 Congruence criteria: SSS, SAS, ASA, AAS, RHS; then apply CPCT.
🟡 Angle Sum = 180°, Exterior Angle = sum of opposite interiors.
🔴 Inequalities: Sum of two sides > third; greater side ↔ greater angle.
✳ Mid-Point Theorem: Mid-segment ∥ third side, half its length.
✔ Widely applied in construction, engineering, design, and daily life.

———————————————————————————————————————————————————————————————————————————–

TEXT BOOK QUESTIONS

Exercise 7.1

🔵 Question
Q1. In quadrilateral ACBD, AC = AD and AB bisects ∠A (see Fig. 7.16). Show that ΔABC ≅ ΔABD.
What can you say about BC and BD?
🟢 Answer
🔵 Step 1: Given AC = AD.
🔵 Step 2: AB bisects ∠A ⇒ ∠CAB = ∠BAD.
🔵 Step 3: AB is common to ΔABC and ΔABD.
🔵 Step 4: Therefore, with AB common, AC = AD, and included angles equal at A,
➡️ By SAS, ΔABC ≅ ΔABD.
🟡 Check: CPCT ⇒ BC = BD.
✔ Final: ΔABC ≅ ΔABD (SAS) and BC = BD.

🔵 Question
Q2. ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see Fig. 7.17). Prove that
(i) ΔABD ≅ ΔBAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.
🟢 Answer
🔵 Step 1: In ΔDAB and ΔCBA:
🟢 – AD = BC (given)
🟢 – AB is common
🟢 – ∠DAB = ∠CBA (given)
🔵 Step 2: The equal angle is included between the equal sides AD, AB and BC, AB respectively.
➡️ By SAS, ΔDAB ≅ ΔCBA i.e., ΔABD ≅ ΔBAC.
✔ Final (i): ΔABD ≅ ΔBAC (SAS).
🟡 Check (CPCT):
🔵 Step 3: From congruence, BD = AC.
✔ Final (ii): BD = AC.
🔵 Step 4: Also by CPCT, ∠ABD = ∠BAC.
✔ Final (iii): ∠ABD = ∠BAC.

🔵 Question
Q3. AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.
🟢 Answer
🔵 Step 1: AD ⟂ AB and BC ⟂ AB; also AD = BC (given).
🔵 Step 2: Let CD meet AB at O; we must prove AO = OB.
🔵 Step 3: Consider ΔAOD and ΔBOC.
🟢 – ∠DAO = ∠OBC = 90° (each formed by a perpendicular to AB with AB).
🟢 – ∠AOD = ∠BOC (vertically opposite angles at O).
🟢 – AD = BC (given).
🔵 Step 4: With two angles equal and the corresponding side (adjacent to one of them) equal,
➡️ By AAS, ΔAOD ≅ ΔBOC.
🔵 Step 5: By CPCT, AO = OB.
✔ Final: O is the midpoint of AB, hence CD bisects AB.

🔵 Question
Q4. l and m are two parallel lines intersected by another pair of parallel lines p and q (see Fig. 7.19). Show that ΔABC ≅ ΔCDA.
🟢 Answer
🔵 Step 1: From l ∥ m and p ∥ q, corresponding/alternate interior angles at intersections are equal.
🔵 Step 2: Identify equal angles:
🟢 – ∠ABC = ∠CDA (formed by m with q and l with q; corresponding).
🟢 – ∠ACB = ∠CAD (formed by m with p and l with p; corresponding).
🔵 Step 3: AC is common to both triangles ΔABC and ΔCDA.
🔵 Step 4: Thus two angles and the included side are equal.
➡️ By ASA, ΔABC ≅ ΔCDA.
✔ Final: ΔABC ≅ ΔCDA (ASA).

🔵 Question 5
Line l is the bisector of ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A. Show that:
(i) ΔAPB ≅ ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.
🟢 Answer
🔵 Step 1: Given l bisects ∠A → ∠PAB = ∠QAB.
🔵 Step 2: BP ⟂ AP and BQ ⟂ AQ → ∠APB = ∠AQB = 90°.
🔵 Step 3: AB common.
🔵 Step 4: By AAS criterion: ΔAPB ≅ ΔAQB.
✔ Final (i): ΔAPB ≅ ΔAQB.
🟡 Check: By CPCT, BP = BQ.
✔ Final (ii): BP = BQ ⇒ B equidistant from arms of ∠A.

🔵 Question 6
In Fig. 7.21, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
🟢 Answer
🔵 Step 1: In ΔBAD and ΔEAC:
➤ BA = AD (given)
➤ AC = AE (given)
➤ ∠BAD = ∠EAC (given)
🔵 Step 2: By SAS, ΔBAD ≅ ΔEAC.
🟡 Check: By CPCT, BD = EC and AD = AE.
🔵 Step 3: In quadrilateral BCDE, BC = DE (corresponding parts).
✔ Final: BC = DE.

🔵 Question 7
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB. Show that:
(i) ΔDAP ≅ ΔEBP
(ii) AD = BE
🟢 Answer
🔵 Step 1: P is mid-point → AP = PB.
🔵 Step 2: ∠BAD = ∠ABE (given).
🔵 Step 3: ∠EPA = ∠DPB (given).
🔵 Step 4: By ASA, ΔDAP ≅ ΔEBP.
✔ Final (i): ΔDAP ≅ ΔEBP.
🟡 Check: By CPCT, AD = BE.
✔ Final (ii): AD = BE.

🔵 Question 8
In right triangle ABC, right angled at C, M is mid-point of hypotenuse AB. C is joined to M and produced to D such that DM = CM. Point D is joined to point B. Show that:
(i) ΔAMC ≅ ΔBMD
(ii) ∠DBC is a right angle
(iii) ΔDBC ≅ ΔACB
(iv) CM = ½ AB
🟢 Answer
🔵 Step 1: M is mid-point of hypotenuse → AM = MB.
🔵 Step 2: DM = CM (given).
🔵 Step 3: CM common in ΔAMC and ΔBMD.
🔵 Step 4: By SSS, ΔAMC ≅ ΔBMD.
✔ Final (i): ΔAMC ≅ ΔBMD.
🔵 Step 5: By CPCT, ∠AMC = ∠BMD.
🔵 Step 6: ∠AMC is 90° (angle in semicircle) ⇒ ∠BMD = 90°.
✔ Final (ii): ∠DBC = 90°.
🔵 Step 7: In ΔDBC and ΔACB:
➤ ∠DBC = ∠ACB = 90°.
➤ DB = AC (from congruence).
➤ BC common.
🔵 Step 8: By RHS, ΔDBC ≅ ΔACB.
✔ Final (iii): ΔDBC ≅ ΔACB.
🔵 Step 9: Hypotenuse AB = 2 CM (mid-point of hypotenuse property).
✔ Final (iv): CM = ½ AB.

Exercise 7.2

🔵 Question 1
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
(i) OB = OC
(ii) AO bisects ∠A.
🟢 Answer
🔵 Step 1: In ΔABO and ΔACO:
🟢 – AB = AC (given)
🟢 – ∠ABO = ∠ACO (angle bisectors)
🟢 – AO common.
➡️ By SAS, ΔABO ≅ ΔACO.
✔ Final (i): OB = OC (CPCT).
🔵 Step 2: By CPCT, ∠BAO = ∠CAO ⇒ AO bisects ∠A.
✔ Final (ii): AO bisects ∠A.

🔵 Question 2
In ΔABC, AD is the perpendicular bisector of BC (Fig. 7.30). Show that ΔABC is an isosceles triangle in which AB = AC.
🟢 Answer
🔵 Step 1: AD ⟂ BC and BD = DC (perpendicular bisector).
🔵 Step 2: In ΔABD and ΔACD:
🟢 – BD = DC (given)
🟢 – ∠ADB = ∠ADC = 90°
🟢 – AD common.
➡️ By RHS, ΔABD ≅ ΔACD.
✔ Final: By CPCT, AB = AC, so ΔABC is isosceles.

🔵 Question 3
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (Fig. 7.31). Show that these altitudes are equal.
🟢 Answer
🔵 Step 1: AB = AC (isosceles).
🔵 Step 2: In ΔABE and ΔACF:
🟢 – AB = AC (given)
🟢 – ∠AEB = ∠AFC = 90° (altitudes)
🟢 – ∠BAE = ∠CAF (common angle at A).
➡️ By AAS, ΔABE ≅ ΔACF.
✔ Final: By CPCT, BE = CF.

🔵 Question 4
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (Fig. 7.32). Show that:
(i) ΔABE ≅ ΔACF
(ii) AB = AC, i.e., ABC is isosceles.
🟢 Answer
(i) ΔABE ≅ ΔACF
🔵 Step 1: BE = CF (given).
🔵 Step 2: ∠AEB = ∠AFC = 90° (altitudes).
🔵 Step 3: ∠BAE = ∠CAF (common angle at A).
➡️ By AAS, ΔABE ≅ ΔACF.
✔ Final (i): ΔABE ≅ ΔACF.
(ii) AB = AC
🔵 Step 4: By CPCT, AB = AC.
✔ Final (ii): ABC is isosceles.

🔵 Question 5
ABC and DBC are two isosceles triangles on the same base BC (Fig. 7.33). Show that ∠ABD = ∠ACD.
🟢 Answer
🔵 Step 1: AB = AC and DB = DC (isosceles property).
🔵 Step 2: Join AD. Consider ΔABD and ΔACD.
🟢 – AB = AC
🟢 – BD = DC
🟢 – AD common.
➡️ By SSS, ΔABD ≅ ΔACD.
✔ Final: By CPCT, ∠ABD = ∠ACD.

🔵 Question 6
ΔABC is isosceles with AB = AC. Side BA is produced to D such that AD = AB (Fig. 7.34). Show that ∠BCD is a right angle.
🟢 Answer
🔵 Step 1: Join CD. In ΔABC, AB = AC. Extend BA to D with AD = AB.
🔵 Step 2: In ΔADC and ΔABC:
🟢 – AD = AB
🟢 – AC common
🟢 – DC = BC (subtracting common segments after adding AD)
🔵 Step 3: By SAS, ΔADC ≅ ΔABC.
🔵 Step 4: Angles at C satisfy ∠ACD + ∠BCD = 180°. Use congruence to show ∠ACD = ∠ACB.
🔵 Step 5: Therefore 2∠BCD = 180°.
✔ Final: ∠BCD = 90°.

🔵 Question 7
ABC is a right-angled triangle in which ∠A = 90°. Find ∠B and ∠C.
🟢 Answer
🔵 Step 1: In a triangle, sum of angles = 180°.
🔵 Step 2: ∠A = 90°. Let ∠B = x, ∠C = y.
🔵 Step 3: x + y + 90 = 180 ⇒ x + y = 90.
✔ Final: ∠B and ∠C are complementary: ∠B + ∠C = 90°.

🔵 Question 8
Show that the angles of an equilateral triangle are 60° each.
🟢 Answer
🔵 Step 1: In an equilateral triangle, all sides are equal.
🔵 Step 2: Therefore, all angles opposite equal sides are equal.
🔵 Step 3: Sum of angles = 180°. Let each angle = x.
🔵 Step 4: 3x = 180 ⇒ x = 60.
✔ Final: Each angle = 60°.

Exercise 7.3

🔵 Question 1
ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
(i) ΔABD ≅ ΔACD
(ii) ΔABP ≅ ΔACP
(iii) AP bisects ∠A and ∠D
(iv) AP is the perpendicular bisector of BC.
🟢 Answer
(i) ΔABD ≅ ΔACD
🔵 Step 1: AB = AC and DB = DC (isosceles triangles on BC).
🔵 Step 2: AD common.
➡️ By SSS, ΔABD ≅ ΔACD. ✔
(ii) ΔABP ≅ ΔACP
🔵 Step 3: From (i), AB = AC. BP = CP (AP bisector property to be shown). Use congruence of triangles with AP common.
➡️ By SAS, ΔABP ≅ ΔACP. ✔
(iii) AP bisects ∠A and ∠D
🔵 Step 4: From congruence (ii), ∠BAP = ∠PAC and ∠BDA = ∠ADC.
✔ AP bisects both ∠A and ∠D.
(iv) AP is the perpendicular bisector of BC
🔵 Step 5: From congruence, BP = PC and ∠BPA = ∠CPA = 90°.
✔ Final: AP ⟂ BC and bisects BC.

🔵 Question 2
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that:
(i) AD bisects BC
(ii) AD bisects ∠A.
🟢 Answer
(i) AD bisects BC
🔵 Step 1: AD ⟂ BC, AB = AC.
🔵 Step 2: In ΔABD and ΔACD:
🟢 – AB = AC
🟢 – ∠ADB = ∠ADC = 90°
🟢 – AD common.
➡️ By RHS, ΔABD ≅ ΔACD.
🔵 Step 3: By CPCT, BD = DC. ✔
(ii) AD bisects ∠A
🔵 Step 4: From CPCT, ∠BAD = ∠CAD.
✔ Final: AD bisects ∠A.

🔵 Question 3
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR. Show that:
(i) ΔABM ≅ ΔPQN
(ii) ΔABC ≅ ΔPQR.
🟢 Answer
(i) ΔABM ≅ ΔPQN
🔵 Step 1: AB = PQ, BC = QR, AM = PN (given).
🔵 Step 2: BM = ½ BC, QN = ½ QR (median property). Thus BM = QN.
➡️ By SSS, ΔABM ≅ ΔPQN. ✔
(ii) ΔABC ≅ ΔPQR
🔵 Step 3: Using medians and SSS for larger triangles, AB = PQ, BC = QR, AC = PR (derived from medians).
➡️ By SSS, ΔABC ≅ ΔPQR. ✔

🔵 Question 4
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
🟢 Answer
🔵 Step 1: BE = CF (given), BE ⟂ AC, CF ⟂ AB.
🔵 Step 2: In ΔBCE and ΔCBF:
🟢 – BE = CF (altitudes equal).
🟢 – ∠BEC = ∠CFB = 90°.
🟢 – BC common.
➡️ By RHS, ΔBCE ≅ ΔCBF.
🔵 Step 3: By CPCT, CE = BF ⇒ AB = AC.
✔ Final: ΔABC is isosceles.

🔵 Question 5
ABC is an isosceles triangle with AB = AC. Draw AP ⟂ BC to show that ∠B = ∠C.
🟢 Answer
🔵 Step 1: In ΔABP and ΔACP:
🟢 – AB = AC (given).
🟢 – ∠APB = ∠APC = 90° (AP ⟂ BC).
🟢 – AP common.
➡️ By RHS, ΔABP ≅ ΔACP.
🔵 Step 2: By CPCT, ∠B = ∠C.
✔ Final: ∠B = ∠C in isosceles ΔABC.

———————————————————————————————————————————————————————————————————————————–

OTHER IMPORTANT QUESTIONS FOR EXAMS

🔵 Section A (Q1–Q6, 1 mark each: VSA/Objective)
🔵 Question 1 (MCQ)
If two triangles are congruent by SSS, then which statement is always true?
🟢 A) Their perimeters are equal
🟡 B) Their areas are equal
🔵 C) All corresponding angles are equal
🔴 D) Only the included angles are equal
🟢 Answer
✔ Final: C) All corresponding angles are equal (by CPCT).

🔵 Question 2 (MCQ)
In ΔABC, ∠A = 90°. The suitable congruence criterion to prove ΔABC ≅ ΔPQR (with ∠P = 90°) using sides AC, AB and QR is:
🟢 A) SAS
🟡 B) ASA
🔵 C) RHS
🔴 D) SSS
🟢 Answer
✔ Final: C) RHS.

🔵 Question 3
State the Angle Sum Property of a triangle.
🟢 Answer
✔ Final: The sum of the three interior angles of a triangle is 180°.

🔵 Question 4 (MCQ)
In an isosceles triangle, the angles at the base are:
🟢 A) Supplementary
🟡 B) Complementary
🔵 C) Equal
🔴 D) Unequal
🟢 Answer
✔ Final: C) Equal.

🔵 Question 5
Fill in the blank: If AB = AC in ΔABC, then ∠ABC = ____.
🟢 Answer
✔ Final: ∠ACB (base angles opposite equal sides are equal).

🔵 Question 6 (MCQ)
Which set of lengths can form a triangle?
🟢 A) 2 cm, 3 cm, 6 cm
🟡 B) 5 cm, 7 cm, 12 cm
🔵 C) 4 cm, 5 cm, 8 cm
🔴 D) 6 cm, 9 cm, 15 cm
🟢 Answer
➤ Check triangle inequality: sum of any two > third.
✔ Final: C) 4, 5, 8 (since 4+5>8, 5+8>4, 4+8>5).

🟢 Section B (Q7–Q12, 2 marks each: Short Answer–I)
🔵 Question 7
In ΔPQR, if ∠P = 58° and ∠Q = 67°, find ∠R.
🟢 Answer
➤ Formula: ∠P + ∠Q + ∠R = 180°.
➤ Substitution: 58 + 67 + ∠R = 180.
➤ Simplification: ∠R = 180 − 125 = 55.
✔ Final: 55°.

🔵 Question 8
ΔABC is isosceles with AB = AC. Prove that the bisector of ∠A is perpendicular to BC.
🟢 Answer
➤ Draw AD such that AD bisects ∠A.
➤ In ΔABD and ΔACD: AB = AC (given).
➤ ∠BAD = ∠CAD (construction).
➤ AD is common.
➤ By SAS, ΔABD ≅ ΔACD.
➤ By CPCT: ∠ADB = ∠ADC.
➤ But ∠ADB + ∠ADC = 180° (linear pair).
➤ Therefore each = 90°.
✔ Final: AD ⟂ BC.

🔵 Question 9 (MCQ)
Which congruence cannot be concluded from “two angles and the included side” being equal?
🟢 A) ASA
🟡 B) AAS
🔵 C) SAS
🔴 D) None of these
🟢 Answer
✔ Final: C) SAS (uses two sides and the included angle, not two angles and the included side).

🔵 Question 10
In ΔXYZ, XY = XZ and XM is drawn to YZ such that M is the midpoint of YZ. Show that XM ⟂ YZ.
🟢 Answer
➤ In ΔXYM and ΔXZM: XY = XZ (given).
➤ YM = MZ (midpoint).
➤ XM common.
➤ By SSS, ΔXYM ≅ ΔXZM.
➤ By CPCT, ∠YMX = ∠XMZ.
➤ Linear pair: ∠YMX + ∠XMZ = 180°.
➤ Therefore each = 90°.
✔ Final: XM ⟂ YZ.

🔵 Question 11
Two sides of ΔABC are 7 cm and 10 cm. What range can the third side take?
🟢 Answer
➤ Triangle inequality: |7 − 10| < third < 7 + 10.
➤ Simplification: 3 < third < 17.
✔ Final: (3 cm, 17 cm) (strictly between).

🔵 Question 12 (MCQ)
If ΔDEF ≅ ΔPQR by ASA, which of the following is not necessarily true?
🟢 A) ∠E = ∠Q
🟡 B) DE = PQ
🔵 C) EF = QR
🔴 D) DF = PR
🟢 Answer
✔ Final: C) EF = QR is not guaranteed by ASA alone unless it’s the corresponding included side; ASA fixes one side (the included side), not necessarily every side until CPCT is invoked with correct correspondence.

🟡 Section C (Q13–22, 3 marks each)
🔵 Question 13
Prove that the sum of any two sides of a triangle is greater than the third side.
🟢 Answer
➤ Draw ΔABC. Extend BA beyond A to point D so that AD = AC.
➤ Join C to D.
➤ ∠ADC < 180° ⇒ ∠ADC + ∠ACD = 180°.
➤ Using exterior angle property: ∠ADC > ∠ABC ⇒ BD > BC.
➤ Substitute BD = BA + AD = BA + AC.
✔ Final: AB + AC > BC (similarly for other pairs).

🔵 Question 14
In ΔXYZ, ∠X = 50°, ∠Y = 60°. Find ∠Z and classify the triangle by its angles.
🟢 Answer
➤ ∠X + ∠Y + ∠Z = 180°.
➤ 50 + 60 + ∠Z = 180 ⇒ ∠Z = 70°.
✔ Final: Angles are all < 90° ⇒ Acute-angled triangle.

🔵 Question 15
In ΔPQR, PQ = PR and PS is drawn bisecting ∠QPR to meet QR at S. Prove that QS = SR.
🟢 Answer
➤ In ΔPQS and ΔPRS:
🟢 – PQ = PR (given).
🟢 – ∠QPS = ∠RPS (angle bisector).
🟢 – PS common.
➡️ By SAS, ΔPQS ≅ ΔPRS.
✔ Final: QS = SR (by CPCT).

🔵 Question 16
Show that the medians of a triangle intersect at a single point (centroid). (Hint: Use congruence of triangles formed by medians.)
🟢 Answer
➤ Let medians AD, BE, CF intersect at G.
➤ Consider ΔAGB and ΔAGC:
🟢 – BG = GC (median divides opposite side).
🟢 – AG common.
🟢 – ∠AGB = ∠AGC (vertically opposite).
➡️ ΔAGB ≅ ΔAGC ⇒ BG = GC.
➤ Similarly for other pairs.
✔ Final: All medians meet at G, the centroid.

🔵 Question 17
The bisectors of two equal angles of a triangle are equal. Prove that the triangle is isosceles.
🟢 Answer
➤ Let ΔABC with ∠B = ∠C. Bisectors BD and CE drawn to AC and AB.
➤ In ΔABD and ΔACE:
🟢 – ∠B = ∠C (given).
🟢 – BD = CE (given).
🟢 – ∠ABD = ∠ACE (corresponding).
➡️ ΔABD ≅ ΔACE ⇒ AB = AC.
✔ Final: ΔABC is isosceles.

🔵 Question 18
Prove that the line joining the mid-points of two sides of a triangle is parallel to the third side.
🟢 Answer
➤ Let D, E mid-points of AB and AC in ΔABC. Join DE.
➤ In ΔADE and ΔCDE: AD = DC, AE = EB.
➤ Use congruence to show ∠ADE = ∠CDE.
➡️ DE ∥ BC (mid-point theorem).
✔ Final: DE ∥ BC and DE = ½ BC.

🔵 Question 19
In ΔXYZ, XM and YN are medians intersecting at G. Prove that 3 × XG = 2 × XM.
🟢 Answer
➤ G is centroid → divides each median in 2:1 ratio.
➤ Hence XG : GM = 2:1.
➤ Multiply: 3 × XG = 2 × XM.
✔ Final: 3XG = 2XM.

🔵 New Question 20
In ΔDEF, DG is drawn from vertex D to side EF such that ∠EDG = ∠FDG. Prove that EG = GF.

🟢 Answer
➤ DG bisects ∠EDF because ∠EDG = ∠FDG.
➤ In ΔEDG and ΔFDG:
🟢 – ∠EDG = ∠FDG (given).
🟢 – DG common.
🟢 – ∠EGD = ∠FGD (vertically opposite angles).
➡️ By AAS, ΔEDG ≅ ΔFDG.
✔ Final: By CPCT, EG = GF.

🔵 Question 21 (Internal Choice)
A. Prove that if two angles of one triangle are equal to two angles of another, the triangles are similar.
OR
B. In ΔABC, ∠B = ∠C. Prove that AD bisects ∠A if and only if BD = CD.
🟢 Answer (A)
➤ Let ΔABC and ΔDEF with ∠A = ∠D, ∠B = ∠E.
➤ Then ∠C = ∠F by angle sum property.
✔ Final: ΔABC ∼ ΔDEF (AAA similarity).

🔵 Question 22
In ΔPQR, prove that the greater angle lies opposite the greater side.
🟢 Answer
➤ Assume PQ > PR.
➤ Construct PS on PQ such that PS = PR. Join S to R.
➤ ∠SRP < ∠Q (by exterior angle property).
✔ Final: Greater angle lies opposite greater side.

🔴 Question 23
Prove that the line joining the mid-points of two sides of a triangle is parallel to the third side and equal to half of it.
🟢 Answer
➤ Let D, E be mid-points of AB and AC in ΔABC. Join DE.
➤ Draw CF ∥ DE through C to meet extended AB at F.
➤ Use congruence of ΔADE and ΔCFE: AD = CF, AE = CE (mid-points), ∠ADE = ∠CFE.
➤ By SAS, ΔADE ≅ ΔCFE.
➤ Thus DE ∥ BC and DE = ½ BC.
✔ Final: Mid-point theorem is proved.

🔴 Question 24 (Internal Choice)
A. Prove that the angle bisectors of a triangle intersect in a point called the in-centre, which is equidistant from the three sides.
OR
B. Two equal chords of a circle are equidistant from the centre. (Though circle concept, used with triangle congruence).
🟢 Answer (A)
➤ Draw ΔABC, bisectors AD, BE, CF intersect at I.
➤ Take ΔABI and ΔACI: ∠BAI = ∠CAI (AD bisector), AI common.
➤ Similarly for others, conclude I is equidistant from sides.
✔ Final: In-centre equidistant from sides.

🔴 Question 25
Prove: Sum of the lengths of any two sides of a triangle is greater than the third side.
🟢 Answer
➤ Construct ΔABC. Extend BA to D so AD = AC.
➤ Join C to D.
➤ Exterior angle ∠ADC > ∠ABC ⇒ CD > BC.
➤ CD = AD + AC = AB + AC.
✔ Final: AB + AC > BC.

🔴 Question 26 (Internal Choice)
A. In ΔPQR, PS is median. Show: PQ² + PR² = 2(PS² + QS²).
OR
B. State and prove the Converse of Isosceles Triangle Theorem.
🟢 Answer (B)
➤ If two angles of a triangle are equal, their opposite sides are equal.
➤ Let ∠B = ∠C in ΔABC. Draw AD ⟂ BC.
➤ In ΔABD and ΔACD:
🟢 – ∠BAD = ∠CAD (given).
🟢 – AD common.
🟢 – ∠ADB = ∠ADC = 90°.
➡️ By AAS, ΔABD ≅ ΔACD.
✔ Final: AB = AC.

🔴 Question 27
Prove that the medians of a triangle intersect at a point which divides each median in the ratio 2:1.
🟢 Answer
➤ Let medians AD, BE, CF intersect at G.
➤ Consider ΔAGB and ΔAGC: BG = GC, AG common, ∠AGB = ∠AGC.
➡️ ΔAGB ≅ ΔAGC ⇒ AG:GD = 2:1 using area arguments.
✔ Final: Centroid divides medians 2:1.

🔴 Question 28 (Internal Choice)
A. Prove that in an equilateral triangle, the medians, altitudes, angle bisectors, and perpendicular bisectors coincide.
OR
B. In ΔXYZ, prove that the greater angle lies opposite the greater side.
🟢 Answer (A)
➤ Draw ΔABC equilateral. All sides equal ⇒ all angles 60°.
➤ Bisectors from vertices are also altitudes and medians (symmetry).
✔ Final: All special segments coincide.

🔴 Question 29
Two triangles have sides 5 cm, 7 cm, 9 cm and 5 cm, 7 cm, 9 cm. Prove the triangles are congruent and find the equality of corresponding angles.
🟢 Answer
➤ All three pairs of sides equal ⇒ SSS criterion.
➤ Therefore triangles are congruent.
➤ By CPCT, all corresponding angles equal.
✔ Final: Triangles congruent by SSS; ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R.

🔴 Question 30 (Internal Choice)
A. Prove: In ΔABC, if AD is median, then AB² + AC² = 2(AD² + BD²).
OR
B. Show that the altitudes of a triangle intersect at a single point (orthocentre).
🟢 Answer (B)
➤ Draw ΔXYZ with altitudes XA, YB, ZC intersecting at H.
➤ Use pairwise congruence of smaller triangles to prove concurrency.
✔ Final: Altitudes meet at orthocentre H.

————————————————————————————————————————————————————————————————————————————

MIND MAP

———————————————————————————————————————————————————————————————————————————–