Class : 9 – Math (English) : Lesson 6. Lines and Angles

EXPLANATION & SUMMARY

✨ Detailed Explanation
🔵 1. Basic Geometric Concepts
🔹 Line ➡️ Extends infinitely in both directions.
🔹 Line Segment ➡️ Part of a line with two endpoints.
🔹 Ray ➡️ Has a fixed starting point but extends endlessly in one direction.
🔹 Collinear Points ➡️ Points on the same line.
🔹 Non-collinear Points ➡️ Points not on the same line.
🔹 Angle ➡️ Formed by two rays with a common endpoint called the vertex.
🟢 2. Types of Angles

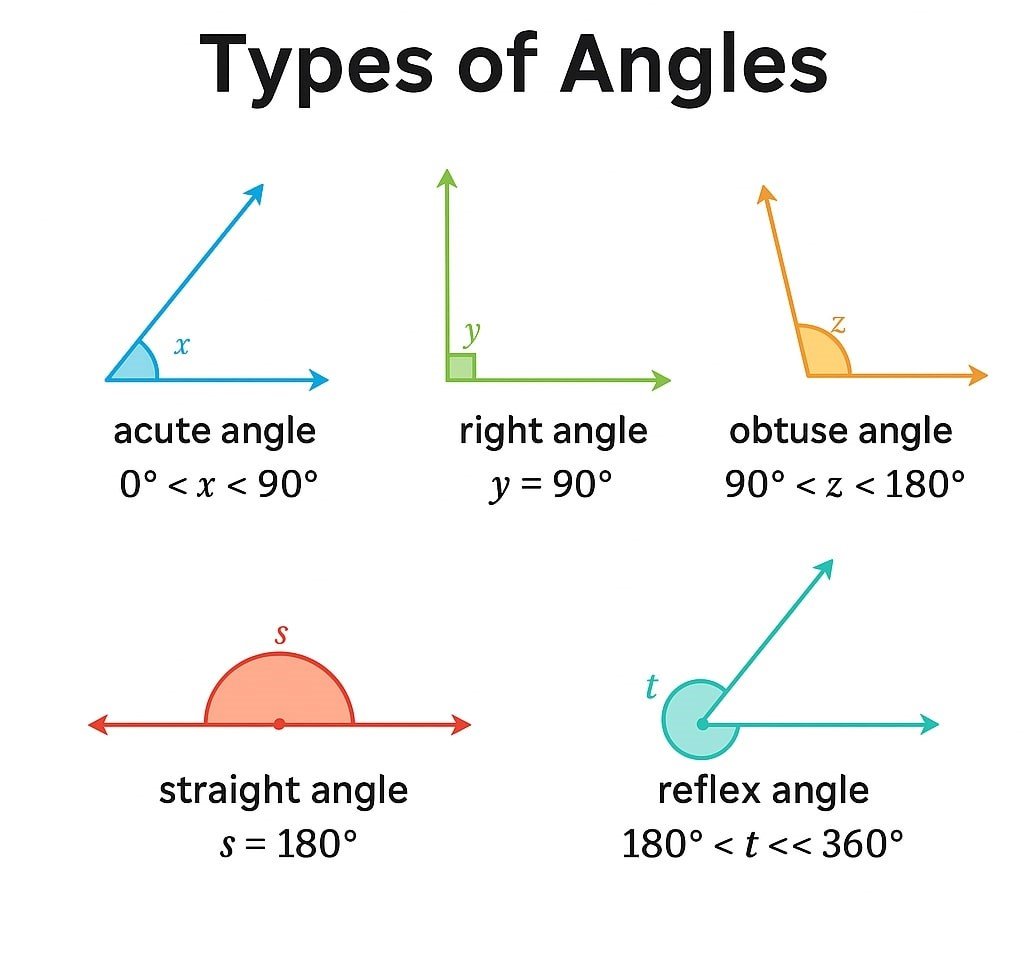
🟩 Acute Angle ➡️ < 90°.
🟩 Right Angle ➡️ = 90°.
🟩 Obtuse Angle ➡️ Between 90°–180°.
🟩 Straight Angle ➡️ = 180°.
🟩 Reflex Angle ➡️ > 180° but < 360°.
🟩 Complementary Angles ➡️ Sum = 90°.
🟩 Supplementary Angles ➡️ Sum = 180°.
✏️ Note: Angles are always measured in degrees (°) unless specified otherwise.
🔴 3. Adjacent Angles and Linear Pairs
🔻 Adjacent Angles ➡️ Share a common vertex and side but do not overlap.
🔻 Linear Pair ➡️ Two adjacent angles whose non-common sides form a straight line; their sum = 180°.
💡 Concept: Linear Pair Axiom – If a ray stands on a line, the adjacent angles form a linear pair and are supplementary.
🟡 4. Vertically Opposite Angles
🟨 When two lines intersect, opposite pairs of angles are called vertically opposite angles.
🟨 Theorem: Vertically opposite angles are equal.
➡️ Reason: Rotational symmetry of intersecting lines ensures equal measure.
🔵 5. Parallel Lines and Transversals
🔷 Parallel Lines ➡️ Two lines in a plane that never meet.
🔷 Transversal ➡️ A line intersecting two or more lines at distinct points.
⚡ Angle Relationships with Transversals
➡️ Corresponding Angles ➡️ Equal.
➡️ Alternate Interior Angles ➡️ Equal.
➡️ Alternate Exterior Angles ➡️ Equal.
➡️ Consecutive (Co-interior) Angles ➡️ Supplementary.
✔️ Converse Statements for Parallelism
✔️ If corresponding angles are equal, lines are parallel.
✔️ If alternate interior angles are equal, lines are parallel.
✔️ If co-interior angles are supplementary, lines are parallel.
🧠 Real-Life Example: Railway tracks are parallel; a bridge crossing them acts as a transversal.
🟢 6. Angle Sum Property of a Triangle
🟩 Statement: The sum of interior angles of any triangle = 180°.
🟩 Proof Idea: Draw a line parallel to one side through the opposite vertex; use alternate interior and corresponding angles.
🔴 7. Exterior Angle Property of a Triangle
🔻 Statement: The exterior angle of a triangle equals the sum of its two opposite interior angles.
🔻 Use: Simplifies solving unknown angles in triangles.
✏️ Note: These properties underpin many geometrical proofs and constructions.
🟡 8. Applications in Problem Solving
🟨 Finding Unknown Angles: Use linear pairs, vertically opposite angles, or transversal properties.
🟨 Triangle Problems: Apply angle sum and exterior angle theorems.
🟨 Parallel Line Deductions: Verify conditions using converses.
💡 Concept: These properties allow architects and engineers to ensure structures are aligned and stable.
🔵 9. Worked Examples (Conceptual)
1️⃣ Example: If two parallel lines are cut by a transversal and one angle = 70°, find all other angles.
🔹 Corresponding = 70°.
🔹 Alternate interior = 70°.
🔹 Co-interior = 110° (because 70° + 110° = 180°).
2️⃣ Example: In a triangle, two angles are 50° and 60°. Find the third angle.
🔹 Sum = 180°.
🔹 Third angle = 180° − (50° + 60°) = 70°.
🟢 10. Avoiding Common Mistakes
🟩 Forgetting to check whether lines are declared parallel before using corresponding or alternate angle properties.
🟩 Mixing up complementary and supplementary angles.
🟩 Misidentifying exterior vs. interior angles.
🔴 11. Connections to Higher Mathematics
🔻 Basis for polygon angle sum formulas.
🔻 Leads into trigonometry (angle relationships).
🔻 Critical in coordinate geometry (slopes and parallelism).
🌿 12. Practical Links
🌿 Road Intersections ➡️ Traffic engineers design angles for smooth flow.
🌿 Sports ➡️ Markings on fields ensure fairness.
🌿 Construction ➡️ Buildings use parallel walls and right angles.
🧠 13. The Importance of Proof
🧠 Geometry builds logical reasoning. Proving properties (like vertically opposite angles) trains step-by-step argumentation.
⚡ 14. Recap of Theorems
⚡ Linear Pair Axiom – Adjacent angles on a line sum to 180°.
⚡ Vertically Opposite Angles Theorem – Equal when two lines intersect.
⚡ Parallel Line Properties – Corresponding/alternate angles equal, co-interior supplementary.
⚡ Converse Statements – Verify parallelism.
⚡ Angle Sum Property – Sum of triangle’s interior angles = 180°.
⚡ Exterior Angle Property – Exterior angle = sum of opposite interior angles.
🔵 15. Logical Flow in Solutions
🔷 Always mark known angles.
🔷 Use diagram labels consistently.
🔷 Write each calculation step separately.
✏️ Note: In exams, clearly state the property used at each step.
🟡 16. Advanced Insight (Beyond Basics)
🟨 Polygon Angle Sum Formula derives from triangle angle sums.
🟨 Alternate interior angle theorem connects with parallel postulate in Euclidean geometry.
🟨 Real-world CAD software uses these relations to maintain precision in models.

📑 Summary (~300 words)
🔵 Key Terms
Line, segment, ray, collinear points, angle.
🟢 Angle Types
Acute (< 90°), Right (= 90°), Obtuse (90°–180°), Straight (= 180°), Reflex (> 180°).
Complementary (sum = 90°), Supplementary (sum = 180°).
🟡 Properties & Axioms
Adjacent angles share a vertex and side.
Linear pair: adjacent angles on a straight line sum to 180°.
Vertically opposite angles: equal when lines intersect.
🔴 Parallel Lines & Transversals
Corresponding, alternate interior, alternate exterior angles: equal.
Co-interior angles: supplementary.
Converses: Use these equalities or sums to prove lines are parallel.
✳️ Triangles
Angle Sum Property: Sum of interior angles = 180°.
Exterior Angle Property: Exterior angle = sum of two opposite interior angles.
⚡ Applications
Used in architecture, engineering, sports field design, and traffic layout.
✔️ Tips
Always label angles clearly.
Check for parallelism before applying transversal properties.
Show every calculation step.
Cite the theorem used in proofs.

📝 Quick Recap
🔵 Lines intersect → Vertically opposite angles equal.
🟢 Linear pair → Adjacent angles on a straight line sum to 180°.
🟡 Parallel lines with transversal → Corresponding/alternate angles equal; co-interior supplementary.
🔴 Triangle → Interior angles sum = 180°; Exterior angle = sum of opposite interior angles.
✳️ Check parallelism using converse statements.
✔️ Real-life links: railway tracks, bridges, road junctions.

———————————————————————————————————————————————————————————————————————————–

TEXT BOOK QUESTIONS

Exercise 6.1

🔵 Question 1
In Fig. 6.13, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.
🟢 Answer
🔵 Step 1: ∠AOC + ∠BOE = 70°.
🔵 Step 2: Vertically opposite: ∠AOC = ∠BOD = 40°.
🔵 Step 3: Substitute: 40° + ∠BOE = 70°.
🔵 Step 4: ∠BOE = 70° − 40° = 30°.
🟡 Check: ∠COE = 180° − ∠AOC = 180° − 40° = 140°.
🔴 Reflex ∠COE = 360° − 140° = 220°.
✔ Final: ∠BOE = 30°, Reflex ∠COE = 220°.

🔵 Question 2
In Fig. 6.14, lines XY and MN intersect at O. If ∠POY = 90° and a : b = 2 : 3, find c.

🟢 Answer

🔵 Step 1: Around O there are three pairs of vertically opposite angles.
🔵 Step 2: Take one set: a + b + 90°.
🔵 Step 3: Sum around a point: (a + b + 90°) + (a + b + 90°) = 360°.
🔵 Step 4: 2(a + b + 90°) = 360° ⟹ a + b + 90° = 180°.
🔵 Step 5: a + b = 90°.
🔵 Step 6: a : b = 2 : 3 ⟹ let a = 2k, b = 3k.
🔵 Step 7: 2k + 3k = 90° ⟹ 5k = 90° ⟹ k = 18°.
🔵 Step 8: a = 36°, b = 54°.
🔵 Step 9: c is vertically opposite to a ⟹ c = a = 36°.
🟡 Check: (a + b + 90°) = 36° + 54° + 90° = 180° ✔
✔ Final: c = 36°.

🔵 Question 3
In Fig. 6.15, ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.
🟢 Answer
🔵 Step 1: Given ∠PQR = ∠PRQ (triangle PQR is isosceles: PQ = PR).
🔵 Step 2: Extend sides to points S and T forming linear pairs at Q and R.
🔵 Step 3: ∠PQS and ∠PQR are linear pair → ∠PQS = 180° − ∠PQR.
🔵 Step 4: ∠PRT and ∠PRQ are linear pair → ∠PRT = 180° − ∠PRQ.
🔵 Step 5: Since ∠PQR = ∠PRQ, their supplements are equal.
✔ Final: ∠PQS = ∠PRT.

🔵 Question 4
In Fig. 6.16, if x + y = w + z, then prove that AOB is a line.
🟢 Answer
🔵 Step 1: Angles around point O: x + y + w + z = 360°.
🔵 Step 2: Given x + y = w + z.
🔵 Step 3: So 2(x + y) = 360°.
🔵 Step 4: x + y = 180°.
🔵 Step 5: Angles on opposite sides sum to 180°, implying AOB forms a straight angle.
✔ Final: AOB is a straight line.

🔵 Question 5
In Fig. 6.17, POQ is a line. Ray OR is perpendicular to PO. OS is another ray between OP and OR. Prove that
∠ROS = ½ (∠QOS − ∠POS).
🟢 Answer
🔵 Step 1: ∠POS + ∠ROS = ∠POR (adjacent).
🔵 Step 2: OR ⟂ PO → ∠POR = 90°.
🔵 Step 3: ∠ROS = 90° − ∠POS.
🔵 Step 4: Similarly, ∠QOS = ∠QOR + ∠ROS.
🔵 Step 5: QO and PO form a straight line → ∠QOR = 90°.
🔵 Step 6: So ∠QOS = 90° + ∠ROS.
🔵 Step 7: Subtract: ∠QOS − ∠POS = (90° + ∠ROS) − ∠POS.
🔵 Step 8: Replace 90° by (∠ROS + ∠POS): Actually from Step 3, 90° = ∠ROS + ∠POS.
🔵 Step 9: ∠QOS − ∠POS = (∠ROS + ∠POS + ∠ROS) − ∠POS = 2∠ROS.
✔ Final: ∠ROS = ½ (∠QOS − ∠POS).

🔵 Question 6
It is given that ∠XYZ = 64° and XY is produced to P. Draw a figure from the information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.
🟢 Answer
🔵 Step 1: ∠XYZ = 64°, so exterior angle ZYP = 180° − 64° = 116°.
🔵 Step 2: YQ bisects ∠ZYP → ∠ZYQ = ∠QYP = 116° / 2 = 58°.
🔵 Step 3: ∠XYQ = ∠XYZ + ∠ZYQ = 64° + 58° = 122°.
🔵 Step 4: Reflex ∠QYP = 360° − ∠QYP = 360° − 58° = 302°.
✔ Final: ∠XYQ = 122°, Reflex ∠QYP = 302°.

Exercise 6.2

🔵 Question 1
In Fig. 6.23, if AB ∥ CD, CD ∥ EF and y : z = 3 : 7, find x.
🟢 Answer
🔵 Step 1: AB, CD, EF are parallel → corresponding angles on the transversal are equal.
🔵 Step 2: y : z = 3 : 7.
🔵 Step 3: y + z = 180° (co-interior angles on parallel lines).
🔵 Step 4: 3k + 7k = 180° → 10k = 180°.
🔵 Step 5: k = 18°.
🔵 Step 6: y = 3×18° = 54°, z = 7×18° = 126°.
🔵 Step 7: x = y = 54° (corresponding).
✔ Final: x = 54°.

🔵 Question 2
In Fig. 6.24, if AB ∥ CD, EF ⟂ CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.
🟢 Answer
🔵 Step 1: EF ⟂ CD → ∠GEF = 90°.
🔵 Step 2: At point E, angles GED and FGE form linear pair: ∠GED + ∠FGE = 180°.
🔵 Step 3: 126° + ∠FGE = 180° → ∠FGE = 54°.
🔵 Step 4: In triangle AGE, ∠AGE + ∠GEF + ∠FGE = 180°.
🔵 Step 5: ∠AGE + 90° + 54° = 180°.
🔵 Step 6: ∠AGE = 180° − 144° = 36°.
✔ Final: ∠AGE = 36°, ∠GEF = 90°, ∠FGE = 54°.

🔵 Question 3
In Fig. 6.25, if PQ ∥ ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS. (Hint: Draw a line parallel to ST through point R.)
🟢 Answer
🔵 Step 1: ∠PQR and ∠QRS are on triangle QRS with PQ ∥ ST.
🔵 Step 2: Exterior angle ∠RST = 130° equals ∠PQR + ∠QRS (parallel line property).
🔵 Step 3: 130° = 110° + ∠QRS.
🔵 Step 4: ∠QRS = 130° − 110° = 20°.
✔ Final: ∠QRS = 20°.

🔵 Question 4
In Fig. 6.26, if AB ∥ CD, ∠APQ = 50° and ∠PRD = 127°, find x and y.
🟢 Answer
🔵 Step 1: ∠PRD = 127° → interior angle with x: x + 127° = 180° (co-interior).
🔵 Step 2: x = 180° − 127° = 53°.
🔵 Step 3: ∠APQ = 50° corresponds to y → y = 50°.
✔ Final: x = 53°, y = 50°.

🔵 Question 5
In Fig. 6.27, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB ∥ CD.
🟢 Answer
🔵 Step 1: Reflection law: Angle of incidence = Angle of reflection at each mirror.
🔵 Step 2: At B, ∠ABC = ∠CBD.
🔵 Step 3: At C, ∠BCD = ∠DC… (angles preserved).
🔵 Step 4: Alternate interior angles on the two parallels are equal, so incident and final rays are parallel.
✔ Final: AB ∥ CD.

———————————————————————————————————————————————————————————————————————————–

OTHER IMPORTANT QUESTIONS FOR EXAMS

🔵 Section A (Q1–Q6, 1 mark each)
🔵 Question 1
A ray stands on a line and forms two adjacent angles 5x° and 7x°. Find x.
🟢 Answer
➤ Formula: Linear pair sum = 180°.
➤ Substitution: 5x + 7x = 180.
➤ Simplification: 12x = 180 → x = 15.
✔ Final: x = 15.

🔵 Question 2 (MCQ)
When two lines intersect, the vertically opposite angles are:
🟢 A) Supplementary
🟡 B) Complementary
🔵 C) Equal
🔴 D) Reflex
🟢 Answer
✔ Final: C) Equal.

🔵 Question 3 (MCQ)
If a transversal cuts two parallel lines, then a pair of co-interior angles are:
🟢 A) Equal
🟡 B) Supplementary
🔵 C) Complementary
🔴 D) Reflex
🟢 Answer
✔ Final: B) Supplementary.

🔵 Question 4
Angles forming a linear pair are in the ratio 2:7. Find the smaller angle.
🟢 Answer
➤ Substitution: Let angles be 2k and 7k.
➤ Linear pair: 2k + 7k = 180.
➤ Simplification: 9k = 180 → k = 20.
✔ Final: Smaller angle = 40°.

🔵 Question 5 (MCQ)
Choose the converse that ensures two lines are parallel:
🟢 A) If corresponding angles are equal, lines are parallel.
🟡 B) If vertically opposite angles are equal, lines are parallel.
🔵 C) If linear-pair sum is 180°, lines are parallel.
🔴 D) If right angles exist, lines are parallel.
🟢 Answer
✔ Final: A.

🔵 Question 6
In a triangle, two interior angles are 52° and 63°. Find the third angle.
🟢 Answer
➤ Formula: Angle sum of triangle = 180°.
➤ Substitution: Third = 180 − (52 + 63).
➤ Simplification: Third = 180 − 115 = 65.
✔ Final: 65°.

🟢 Section B (Q7–Q12, 2 marks each)
🔵 Question 7
Two lines intersect at O. One angle is (3y + 10)° and its vertically opposite angle is (5y − 14)°. Find y and each angle.
🟢 Answer
➤ Vertically opposite: 3y + 10 = 5y − 14.
➤ Simplification: 10 + 14 = 5y − 3y → 24 = 2y → y = 12.
➤ Angle value: 3(12) + 10 = 46; 5(12) − 14 = 46.
✔ Final: y = 12, both angles = 46°.

🔵 Question 8
A transversal cuts two lines. One pair of corresponding angles is (2x − 5)° and (x + 40)°. If the lines are parallel, find x.
🟢 Answer
➤ Corresponding angles (parallel) are equal.
➤ Substitution: 2x − 5 = x + 40.
➤ Simplification: 2x − x = 40 + 5 → x = 45.
✔ Final: x = 45.

🔵 Question 9
In ΔABC, exterior angle at A is 128°. The interior opposite angles at B and C are in ratio 3:5. Find ∠B and ∠C.
🟢 Answer
➤ Exterior angle theorem: ∠A_ext = ∠B + ∠C.
➤ Let ∠B = 3k, ∠C = 5k.
➤ Substitution: 3k + 5k = 128 → 8k = 128.
➤ Simplification: k = 16 → ∠B = 48, ∠C = 80.
✔ Final: ∠B = 48°, ∠C = 80°.

🔵 Question 10 (MCQ)
If two lines are cut by a transversal and alternate interior angles are equal, then the lines are:
🟢 A) Intersecting but not parallel
🟡 B) Perpendicular
🔵 C) Parallel
🔴 D) Skew
🟢 Answer
✔ Final: C) Parallel.

🔵 Question 11
At a point on a straight road, two signposts make angles 68° and 112° with the road on the same side. Show they form a linear pair and write the property used.
🟢 Answer
➤ Substitution: 68 + 112 = 180.
➤ Property: Sum of angles forming a linear pair is 180°.
✔ Final: They form a linear pair (Linear Pair Axiom).

🔵 Question 12
Ray OY is the common arm of ∠XOY and ∠YOZ. If ∠XOY = 4t and ∠YOZ = (6t − 30)°, and OX and OZ are in a straight line, find t.
🟢 Answer
➤ Formula: Linear pair sum = 180°.
➤ Substitution: 4t + (6t − 30) = 180.
➤ Simplification: 10t − 30 = 180 → 10t = 210 → t = 21.
✔ Final: t = 21.
🟡 Section C (Q13–22, 3 marks each)
🔵 Question 13
Two lines intersect at O. One angle is 136°. Find all other three angles and justify.
🟢 Answer
➤ Formula: Vertically opposite angles are equal.
➤ Substitution: Opposite to 136° is 136°.
➤ Formula: Linear pair sum = 180°.
➤ Substitution: Adjacent angle = 180 − 136.
➤ Simplification: Adjacent angle = 44.
➤ Vertically opposite of 44° is 44°.
✔ Final: Angles = 136°, 44°, 136°, 44° (VOA & Linear Pair).

🔵 Question 14
A transversal cuts two lines l and m. If one pair of corresponding angles are (3x + 10)° and (5x − 38)° and l ∥ m, find x and each corresponding angle.
🟢 Answer
➤ Formula: Corresponding angles (∥) are equal.
➤ Substitution: 3x + 10 = 5x − 38.
➤ Simplification: 10 + 38 = 5x − 3x → 48 = 2x → x = 24.
➤ Angle value: 3(24) + 10 = 82; 5(24) − 38 = 82.
✔ Final: x = 24, each angle = 82°.

🔵 Question 15 (with internal choice)
In ΔABC, the exterior angle at C is 143°. If ∠A = 4y and ∠B = (3y + 1)°, find ∠A and ∠B.
OR
In ΔPQR, exterior angle at R equals 150°. If the interior opposite angles are in ratio 2:3, find those angles.
🟢 Answer
➤ Formula: Exterior angle = sum of remote interior angles.
➤ Substitution: 143 = 4y + (3y + 1).
➤ Simplification: 143 = 7y + 1 → 7y = 142 → y = 20.2857… (not neat).
➤ Check: Keep exact fraction y = 142/7.
➤ Angles: ∠A = 4(142/7) = 568/7 = 81.142857…, ∠B = 3(142/7) + 1 = 426/7 + 1 = 433/7 = 61.857142….
✔ Final: ∠A = 568/7° (≈81.14°), ∠B = 433/7° (≈61.86°).
OR – Solution
➤ Let angles be 2k and 3k.
➤ Substitution: 2k + 3k = 150.
➤ Simplification: 5k = 150 → k = 30.
✔ Final: Interior opposite angles = 60° and 90°.

🔵 Question 16
At a point on a straight line AB, two rays OC and OD lie on the same side such that ∠COB = 37° and ∠AOD = 98°. Find ∠COD and ∠AOC.
🟢 Answer
➤ Formula: Linear pair with the straight line AB gives sums 180°.
➤ Substitution: ∠AOB = 180.
➤ Substitution: ∠AOD + ∠DOB = 180 → 98 + ∠DOB = 180.
➤ Simplification: ∠DOB = 82.
➤ Substitution: ∠COB = 37 → ∠AOC = 180 − 37 = 143.
➤ Angle between OC and OD: ∠COD = ∠COB + ∠BOD = 37 + 82 = 119.
✔ Final: ∠COD = 119°, ∠AOC = 143°.

🔵 Question 17 (with internal choice)
In the figure (describe): l ∥ m, transversal t meets l at E and m at F. If ∠BEt = 65° (interior at E) and ∠tFD is marked as (x + 25)°, find x and write the property used.
OR
Two lines are cut by a transversal. If a pair of co-interior angles are (4x − 5)° and (2x + 25)°, and lines are parallel, find x and each angle.
🟢 Answer
➤ Property: Corresponding or alternate interior equality (choose matching positions).
➤ Substitution: (x + 25) = 65 (for equal corresponding).
➤ Simplification: x = 40.
✔ Final: x = 40; property: Corresponding angles are equal (∥).
OR – Solution
➤ Formula: Co-interior (∥) are supplementary.
➤ Substitution: (4x − 5) + (2x + 25) = 180.
➤ Simplification: 6x + 20 = 180 → 6x = 160 → x = 80/3.
➤ Angles: 4(80/3) − 5 = 320/3 − 5 = 305/3; 2(80/3) + 25 = 160/3 + 25 = 235/3.
✔ Final: Angles = 305/3° (≈101.67°) and 235/3° (≈78.33°).

🔵 Question 18
Prove that if a transversal makes a pair of equal alternate interior angles with two lines, then the lines are parallel.
🟢 Answer
➤ Given: ∠1 = ∠2 (alternate interior).
➤ Construct: Extend to show a linear pair at one vertex.
➤ Reasoning: If lines were not parallel, sum of interior angles on the same side would differ from 180°, contradicting equality with a straight angle.
➤ Euclid’s Postulate/Converse: Equality of alternate interior angles implies parallelism.
✔ Final: Therefore, the two lines are parallel (Converse of Alternate Interior Angle Theorem).

🔵 Question 19
In ΔABC, the exterior angle at B is (7x − 6)° and the interior opposite angles at A and C are (3x − 8)° and (2x + 10)°. Find all three interior angles of the triangle.
🟢 Answer
➤ Formula: Exterior at B = ∠A + ∠C.
➤ Substitution: 7x − 6 = (3x − 8) + (2x + 10).
➤ Simplification: 7x − 6 = 5x + 2 → 2x = 8 → x = 4.
➤ Compute: ∠A = 3(4) − 8 = 4; ∠C = 2(4) + 10 = 18.
➤ Angle sum: ∠B = 180 − (4 + 18) = 158.
✔ Final: ∠A = 4°, ∠B = 158°, ∠C = 18°.

🔵 Question 20 (with internal choice)
Lines a and b are parallel. A transversal cuts them forming an angle of 112° at the upper intersection on the interior left. Find all seven remaining angles at both intersections.
OR
If corresponding angle at the upper intersection is 68°, list the measures of alternate interior, co-interior, and vertically opposite angles.
🟢 Answer
➤ Start: Given an interior angle = 112°.
➤ Linear pair: Adjacent = 180 − 112 = 68.
➤ VOA: Opposite to 112° is 112°; opposite to 68° is 68°.
➤ Corresponding / Alternate transfer to second intersection: same set {112°, 68°}.
✔ Final: Angles across both intersections = four of 112° and four of 68° in standard positions.
OR – Solution
➤ Given corresponding = 68°.
➤ Alternate interior = 68°.
➤ Co-interior partner = 180 − 68 = 112°.
➤ Vertically opposite to 68° = 68°; to 112° = 112°.
✔ Final: Set of measures = 68° (equal families) and 112° (supplements).

🔵 Question 21
In the figure (describe): At O, three rays form angles x°, y°, z° around a straight line AB so that x lies above AB on left, y above AB on right, z below AB. If x : y = 2 : 3 and z is vertically opposite to y, find x, y, z.
🟢 Answer
➤ VOA: z = y.
➤ Linear pair on AB (upper angles on straight line): x + y = 180.
➤ Ratio: x = 2k, y = 3k.
➤ Substitution: 2k + 3k = 180.
➤ Simplification: 5k = 180 → k = 36.
➤ Values: x = 72, y = 108, z = 108.
✔ Final: x = 72°, y = 108°, z = 108°.

🔵 Question 22 (with internal choice)
Through a point P outside a line l, a line m is drawn so that a transversal t makes equal corresponding angles with l and m. Prove that l ∥ m.
OR
Given l ∥ m, and a transversal t meets them at A and B respectively. If ∠tAB = (x + 20)° and the corresponding angle at B is (2x − 10)°, verify parallelism and find x.
🟢 Answer
➤ Given: One pair of corresponding angles equal.
➤ Converse statement: If corresponding angles are equal, the lines are parallel.
➤ Therefore: l ∥ m.
✔ Final: l ∥ m by Converse of Corresponding Angles Postulate.
OR – Solution
➤ Equality for corresponding (∥): x + 20 = 2x − 10.
➤ Simplification: 20 + 10 = 2x − x → 30 = x.
➤ Check: Angles = 50° and 50° (equal).
✔ Final: x = 30; equality confirms parallelism.

🔴 Section D (Q23–30, 4 marks each)
🔵 Question 23
In ΔXYZ, ∠X = 50°, ∠Y = 60°. Find ∠Z. Then draw a line parallel to YZ through X and prove exterior angle property.
🟢 Answer
➤ Formula: Angle sum of triangle = 180°.
➤ Substitution: ∠Z = 180 − (50 + 60).
➤ Simplification: ∠Z = 70.
➤ Draw parallel line through X: exterior angle at X equals sum of opposite interiors.
✔ Final: ∠Z = 70°; exterior angle = 50° + 60° = 110°, confirming the property.

🔵 Question 24 (with internal choice)
Prove: If two lines are parallel, then the sum of the interior angles on the same side of a transversal is 180°.
OR
Prove the converse: If the sum of interior angles on the same side of a transversal is 180°, the lines are parallel.
🟢 Answer
➤ Construction: Draw two parallel lines cut by a transversal.
➤ Using alternate interior angles and linear pair, derive equality.
➤ Conversely, assume sum = 180°, extend lines, contradiction unless lines are parallel.
✔ Final: Both statements proven using transversal properties and Euclid’s postulate.

🔵 Question 25
In ΔPQR, exterior angle at P = 120°, interior opposite angles are in ratio 2:3. Find all angles of the triangle.
🟢 Answer
➤ Let opposite angles = 2k and 3k.
➤ Exterior property: 2k + 3k = 120 → 5k = 120 → k = 24.
➤ Interior: ∠Q = 48°, ∠R = 72°.
➤ ∠P = 180 − (48 + 72) = 60°.
✔ Final: ∠P = 60°, ∠Q = 48°, ∠R = 72°.

🔵 Question 26 (with internal choice)
Two complementary angles differ by 22°. Find both.
OR
Two supplementary angles differ by 50°. Find both.
🟢 Answer
➤ Complementary: Let smaller = x, larger = x + 22.
➤ Sum: x + (x + 22) = 90 → 2x + 22 = 90 → 2x = 68 → x = 34.
➤ Larger = 56.
✔ Final: Angles = 34° and 56°.
OR – Solution
➤ Supplementary: Let smaller = y, larger = y + 50.
➤ Sum: y + (y + 50) = 180 → 2y + 50 = 180 → 2y = 130 → y = 65.
➤ Larger = 115.
✔ Final: Angles = 65° and 115°.

🔵 Question 27
At a junction, three roads form angles around a point: 98°, 125°, and x. Find x. Prove that the sum of angles at a point = 360°.
🟢 Answer
➤ Formula: Angles at a point sum to 360°.
➤ Substitution: 98 + 125 + x = 360.
➤ Simplification: 223 + x = 360 → x = 137.
✔ Final: x = 137°; demonstration confirms angle-sum property.

🔵 Question 28 (with internal choice)
Show that if two lines intersect, the bisectors of vertically opposite angles are in a straight line.
OR
Prove that the bisectors of adjacent supplementary angles are perpendicular.
🟢 Answer
➤ Construction: Draw intersecting lines, label ∠A and ∠B as vertically opposite.
➤ Bisectors halve equal angles → resulting angles adjacent sum to 180°.
➤ Thus, bisectors form a straight line.
✔ Final: Bisectors of vertically opposite angles are collinear.
OR – Solution
➤ Adjacent supplementary: ∠1 + ∠2 = 180°.
➤ Their halves: ½∠1 + ½∠2 = 90°.
➤ Therefore, bisectors meet at right angles.
✔ Final: Bisectors are perpendicular.

🔵 Question 29
In ΔDEF, exterior angle at E is 150°, interior opposite angles at D and F are equal. Find all three interior angles.
🟢 Answer
➤ Let ∠D = ∠F = k.
➤ Exterior at E = ∠D + ∠F = 150 → 2k = 150 → k = 75.
➤ Interior E = 180 − (75 + 75) = 30.
✔ Final: ∠D = 75°, ∠E = 30°, ∠F = 75°.

🔵 Question 30
A straight road and a railway line intersect at a point forming vertically opposite angles of measures 68° and 112°. Show the supplementary and vertically opposite angle relationships.
🟢 Answer
➤ Vertically opposite: Opposite to 68° is 68°; opposite to 112° is 112°.
➤ Linear pairs: 68 + 112 = 180°.
➤ Hence, vertically opposite pairs equal; adjacent pairs supplementary.
✔ Final: Confirmed VOA and supplementary relationships: 68°, 112° pairs.

————————————————————————————————————————————————————————————————————————————

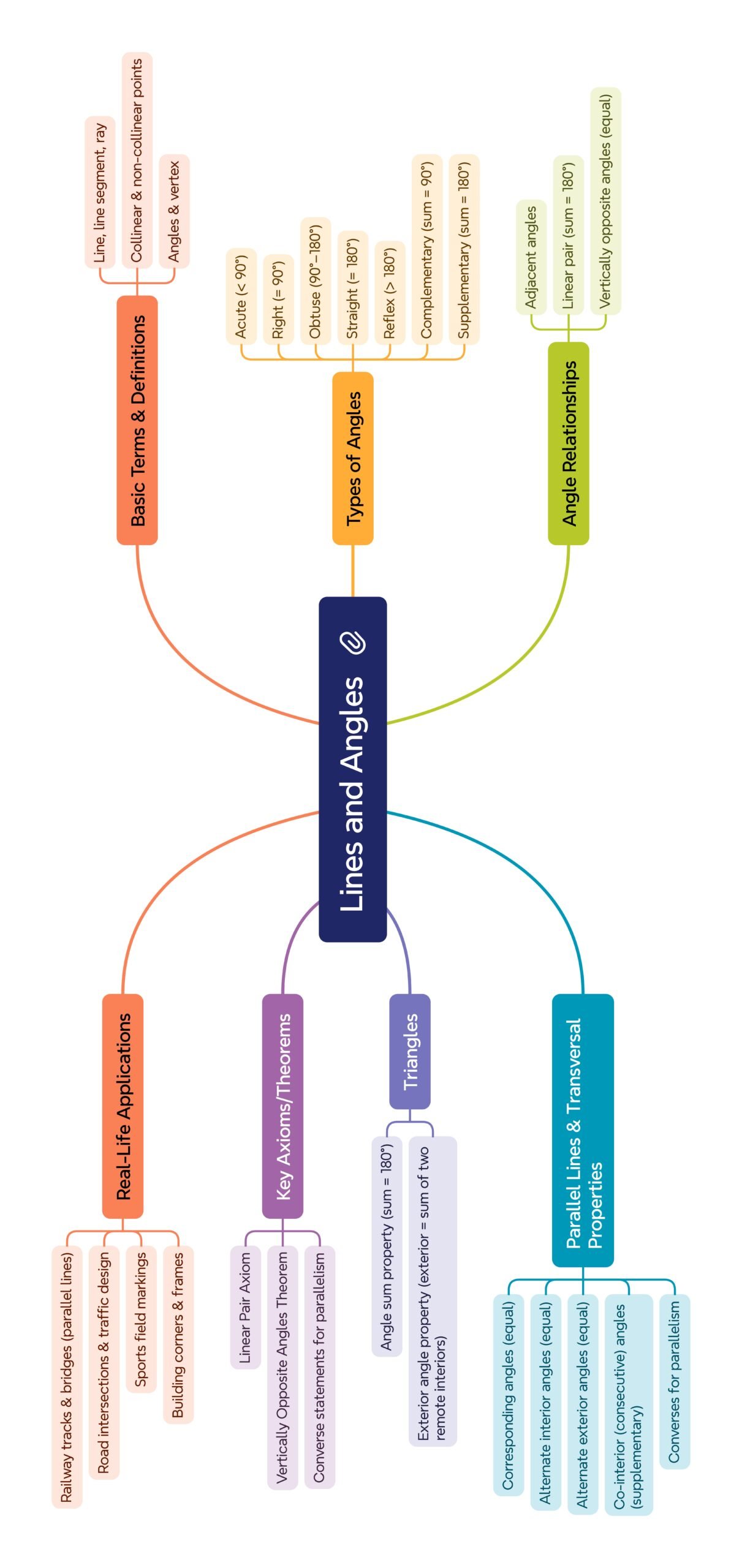
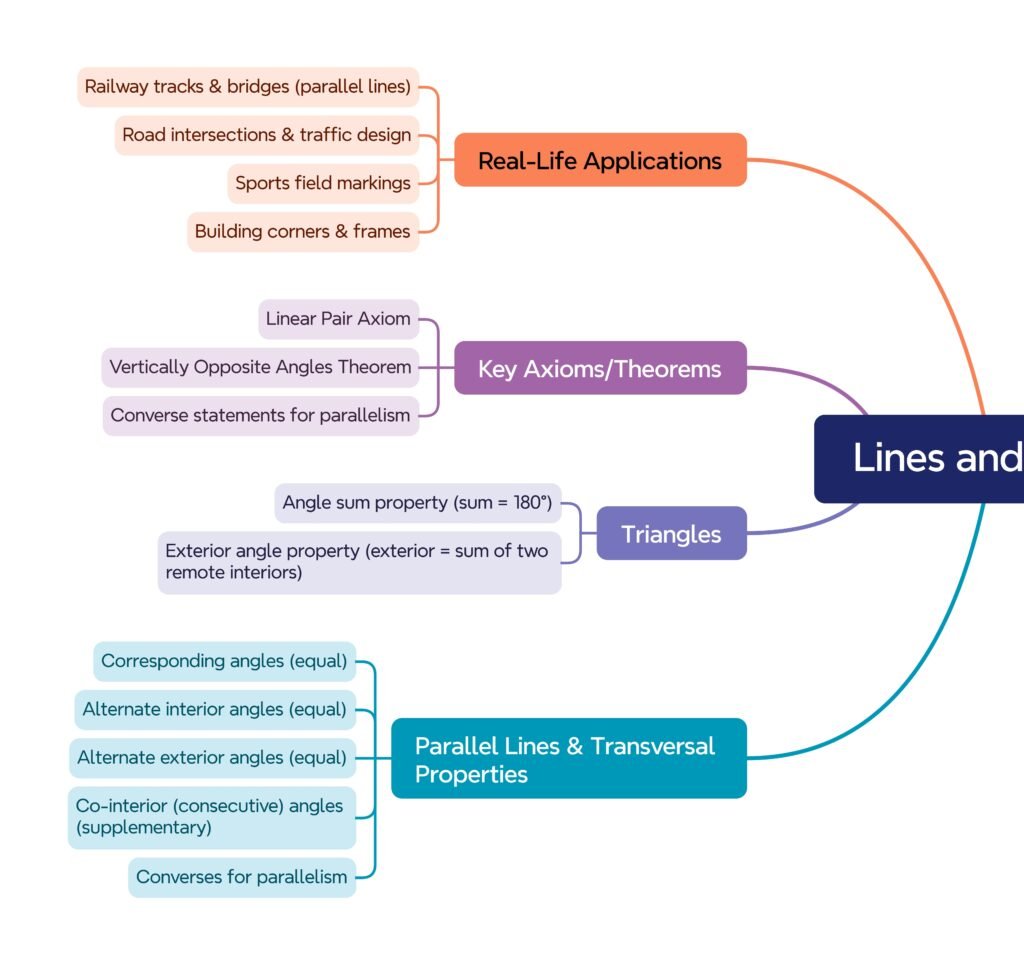
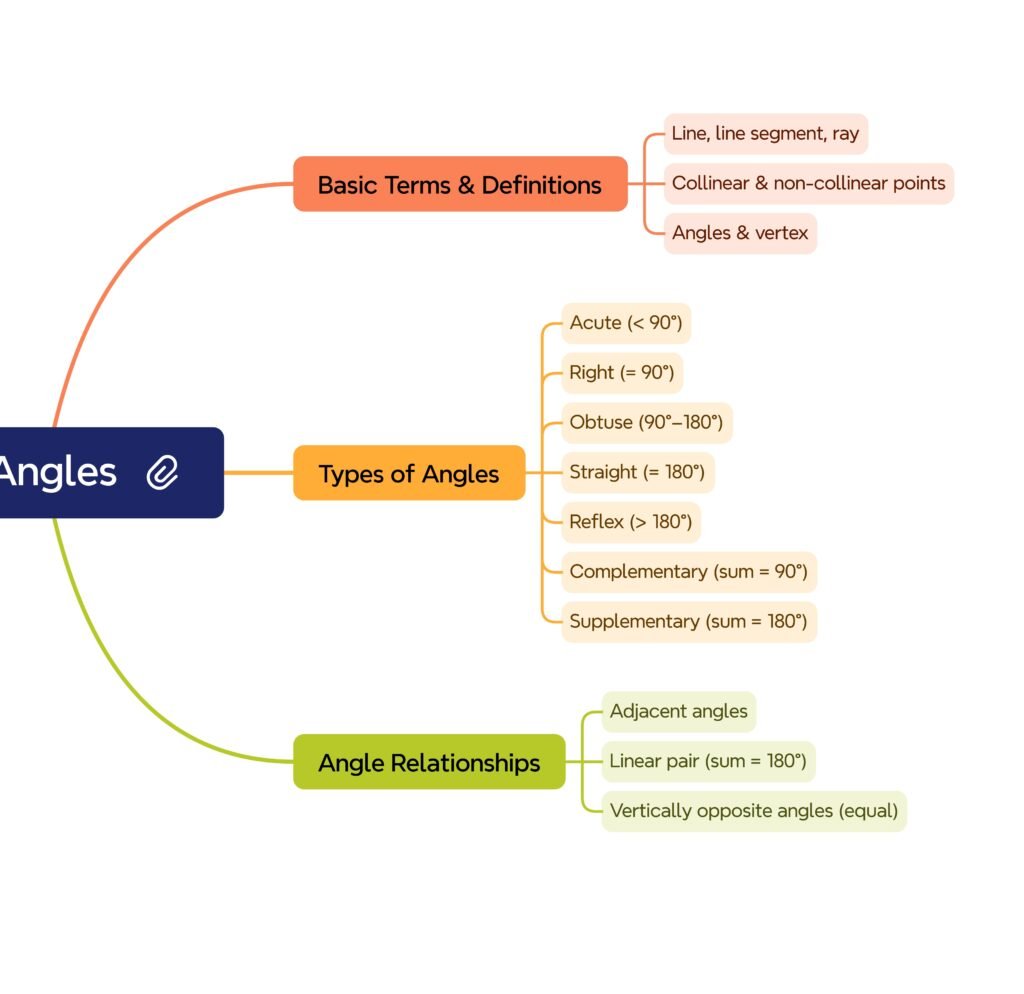
MIND MAP

———————————————————————————————————————————————————————————————————————————–