Class : 9 – Math (English) : Lesson 3. Coordinate Geometry
EXPLANATION & SUMMARY
🔵 Detailed Explanation
🔵 1) Introduction to Coordinate Geometry
🌿 Coordinate Geometry (also called Cartesian Geometry) is the study of geometry using algebra through ordered pairs (x,y).
🔴 It was introduced by René Descartes to represent geometric figures on a plane using numbers.
🟢 Everyday uses: GPS navigation uses coordinates (latitude, longitude) to locate positions.
💡 Concept: A coordinate plane allows us to represent every point uniquely by an ordered pair of numbers.
🟡 2) The Cartesian Plane and Axes
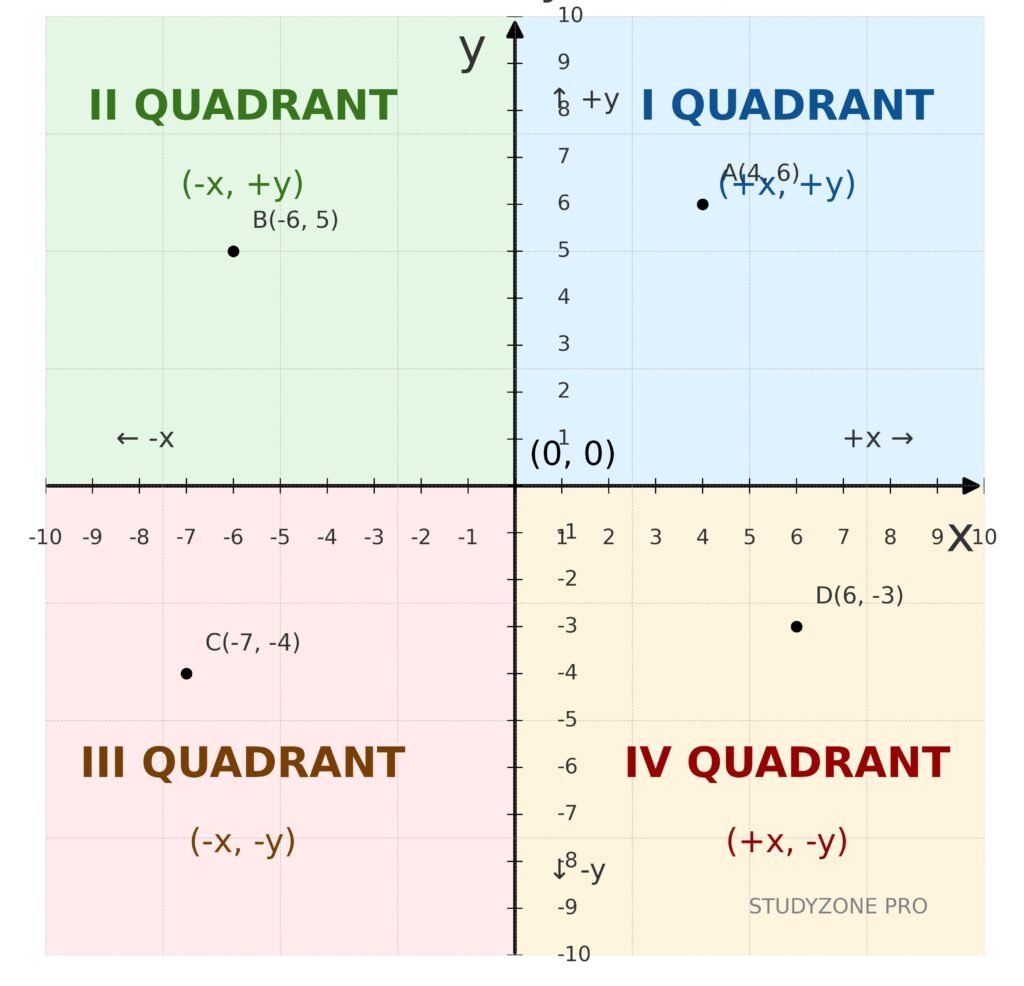
• 🔵 The horizontal line is the x-axis, and the vertical line is the y-axis.
• 🟢 Their intersection is the origin O(0, 0).
• 🔴 The x-axis and y-axis divide the plane into four quadrants numbered counter-clockwise:
1️⃣ Quadrant I: (+x, +y)
2️⃣ Quadrant II: (−x, +y)
3️⃣ Quadrant III: (−x, −y)
4️⃣ Quadrant IV: (+x, −y)
✏️ Note: Always read a coordinate as (x, y) → x-coordinate is first (abscissa), y-coordinate second (ordinate).
🔵 3) Plotting Points
✔️ Step 1: Start at origin O(0, 0).
✔️ Step 2: Move horizontally along x-axis to x-coordinate.
✔️ Step 3: From there, move vertically parallel to y-axis to y-coordinate.
✔️ Step 4: Mark the point and label it.
➡️ Example: Plot P(3, 2). Move 3 units right, 2 units up.
➡️ Example: Plot Q(−4, 1). Move 4 units left, 1 unit up.
🌿 Real-life link: A map grid (e.g., treasure map) uses the same plotting method.
🟢 4) Locating Points in Quadrants
🔴 The signs of (x, y) determine the quadrant:
• (+, +) → Quadrant I
• (−, +) → Quadrant II
• (−, −) → Quadrant III
• (+, −) → Quadrant IV
💡 Concept: Points lying on axes are not in any quadrant—e.g., (0, 5) lies on the y-axis, (7, 0) on the x-axis.
🟡 5) Distance Between Points (Distance Formula)
Although formally derived in Class 10, Class 9 introduces intuition:
For A(x₁,y₁) and B(x₂,y₂),
📌 AB = √((x₂ − x₁)² + (y₂ − y₁)²).
Example: Find distance between A(2, 3) and B(5, 7):
Step 1: x₂−x₁ = 5−2=3.
Step 2: y₂−y₁ = 7−3=4.
Step 3: AB = √(3²+4²) = √(9+16)=√25=5.
✏️ Note: Though NCERT Class 9 mainly covers plotting, this preview builds intuition for Class 10.
🔵 6) Coordinates of Points on Axes and Origin
• 🌿 Origin O: (0, 0).
• 🟢 Point on x-axis: (a, 0) → distance from origin is |a|.
• 🔴 Point on y-axis: (0, b) → distance from origin is |b|.
• 🟡 Symmetry: Points (x,y) and (x,−y) are reflections across x-axis; (−x,y) across y-axis.
🟢 7) Midpoints and Symmetry (Preview)
Midpoint M of segment joining A(x₁,y₁) and B(x₂,y₂):
M = ((x₁ + x₂)/2, (y₁ + y₂)/2).
Example: Midpoint between (−2, 4) and (6, 0) = ((−2+6)/2, (4+0)/2) = (4/2, 4/2)=(2, 2).
🔴 Symmetry facts help predict positions without plotting each time.
🟡 8) Applications of Coordinate Geometry
• 📍 Maps & Navigation: GPS uses coordinates to locate places.
• 📊 Data Visualization: Graphs of functions or statistics.
• 🏗 Engineering: CAD software places points by coordinates.
• 🎮 Gaming: Game engines track object positions in a 2D plane.
💡 Concept: Any motion or shape on a plane can be represented numerically, bridging algebra and geometry.
🔵 9) Real-life Example Problem
“On a treasure map, the starting point is at (0, 0). The first clue is at (−3, 4). The next is at (5, −2). Plot them to trace the path.”
➡️ Quadrant analysis: (−3, 4) → Quadrant II, (5, −2) → Quadrant IV.
🟢 10) Summary of Quadrant Signs Table
✏️ Note (copy-paste friendly):
Quadrant I: (+x, +y)
Quadrant II: (−x, +y)
Quadrant III: (−x, −y)
Quadrant IV: (+x, −y)
🔴 11) History and Development
⚡ René Descartes introduced the Cartesian system in the 17th century. It united algebra and geometry, revolutionising mathematics.
🌿 Fun fact: The name “Cartesian” comes from “Cartesius,” the Latin form of Descartes.
🟡 12) Practice & Self-Check Ideas
1️⃣ Plot points: A(4, 5), B(−2, 3), C(−3, −5), D(6, −1). Identify quadrants.
2️⃣ Determine coordinates of points on axes: P on x-axis at distance 7, Q on y-axis at distance 9.
3️⃣ Find midpoint of E(−4, 2) and F(2, −6).
4️⃣ Use distance formula preview: distance between (−1, 3) and (2, −1).
🔵 13) Common Mistakes to Avoid
• Mixing up x and y while plotting.
• Using clockwise instead of counter-clockwise numbering of quadrants.
• Forgetting that points on axes are not in quadrants.
• Misplacing negative signs when moving left or down.
💡 Concept: Always double-check the sign of each coordinate.
🟢 14) Higher-Order Thinking
• Symmetry helps reduce work: reflection across axes predicts points.
• The origin acts as a rotational center: rotating a point (x,y) by 180° → (−x, −y).
• Coordinate geometry provides algebraic proofs for geometric theorems (e.g., slopes of perpendicular lines).
🟡 15) Real-World Connections
✔️ Computer graphics engines map screen pixels using coordinates.
✔️ Economics: Demand–supply graphs are plotted in coordinate planes.
✔️ Meteorology: Weather data visualisations use coordinates to show trends.
🔴 16) Wrap-up Thought
Coordinate geometry bridges arithmetic, algebra, and geometry, making abstract shapes measurable and computable.
🟣 Summary (~300 words)
Introduction & Plane:
• Coordinate geometry locates points using ordered pairs (x,y) on a Cartesian plane.
• x-axis (horizontal) and y-axis (vertical) intersect at origin O(0,0).
Quadrants & Signs:
• Quadrants numbered counter-clockwise: I(+,+), II(−,+), III(−,−), IV(+,−).
• Points on axes are not in any quadrant.
Plotting Points:
• Start at origin → move along x-axis → then move parallel to y-axis.
• Example: P(3,2) is 3 right, 2 up.
Distance & Midpoint (Preview):
• Distance between A(x₁,y₁) and B(x₂,y₂): √((x₂−x₁)²+(y₂−y₁)²).
• Midpoint of segment joining two points: ((x₁+x₂)/2,(y₁+y₂)/2).
Symmetry:
• Reflection: (x,y) across x-axis → (x,−y); across y-axis → (−x,y).
• Rotation: (x,y) rotated 180° about origin → (−x,−y).
Applications:
• GPS, maps, engineering CAD, economics graphs, computer graphics, and gaming engines all rely on coordinate geometry.
Historical Note:
• René Descartes introduced the Cartesian system in the 17th century, uniting algebra and geometry.
Common Mistakes:
• Interchanging x and y.
• Wrong quadrant numbering.
• Forgetting axis points’ special case.
Coordinate geometry provides a foundation for advanced topics such as straight lines, slopes, and analytical proofs. It allows visualization of algebraic equations as geometric objects, making abstract problems tangible. Mastering plotting, quadrant rules, and symmetry ensures confidence for higher classes.
📝 Quick Recap
🔵 Cartesian plane: x-axis (horizontal), y-axis (vertical), origin O(0,0).
🟢 Quadrants: I(+,+), II(−,+), III(−,−), IV(+,−).
🟡 Plotting: move along x then y.
🔴 Points on axes: not in quadrants.
🔵 Distance formula preview: √((x₂−x₁)²+(y₂−y₁)²).
🟢 Midpoint: ((x₁+x₂)/2,(y₁+y₂)/2).
✨ Applications: GPS, CAD, graphs, gaming.

———————————————————————————————————————————————————————————————————————————–
TEXT BOOK QUESTIONS
Exercise 3.1
🔵 Question 1
How will you describe the position of a table lamp on your study table to another person?
🟢 Answer
🔵 Step 1: Fix two perpendicular reference lines along the edges of the study table (like x-axis and y-axis).
🔵 Step 2: Measure the distances of the lamp from the two adjacent edges to get coordinates (x, y).
🔵 Step 3: State the position as an ordered pair relative to the chosen axes.
✔️ Final: Describe the lamp’s position by giving two perpendicular distances (x, y) from fixed edges, similar to coordinates.
🔵 Question 2
(Street Plan): A city has two main roads which cross each other at the centre of the city. These two roads are along the North–South direction and East–West direction.
🟢 Answer
🔵 Step 1: Represent the two roads as perpendicular axes—North–South as the y-axis and East–West as the x-axis.
🔵 Step 2: The crossing point at the centre of the city is the origin (0, 0).
🔵 Step 3: Any location in the city can be described using an ordered pair (x, y) where x is the distance east or west and y is the distance north or south from the centre.
✔️ Final: The two roads act like coordinate axes, and positions in the city are described using coordinates relative to the crossing point.
Exercise 3.2
🔵 Question 1(i)
What is the name of horizontal and vertical lines drawn to determine the position of any point in the Cartesian plane?
🟢 Answer
🔵 Step 1: Horizontal line → x-axis.
🔵 Step 2: Vertical line → y-axis.
✔️ Final: x-axis and y-axis
🔵 Question 1(ii)
What is the name of each part of the plane formed by these two lines?
🟢 Answer
🔵 Step 1: The plane is divided into four parts.
✔️ Final: Quadrants
🔵 Question 1(iii)
Write the name of the point where these two lines intersect.
🟢 Answer
✔️ Final: Origin
🔵 Question 2(i)
The coordinates of B.
🟢 Answer
🔵 Step 1: From Fig. 3.14, B is at (−4, 3).
✔️ Final: (−4, 3)
🔵 Question 2(ii)
The coordinates of C.
🟢 Answer
✔️ Final: (5, −5)
🔵 Question 2(iii)
The point identified by the coordinates (−3, −5).
🟢 Answer
✔️ Final: E
🔵 Question 2(iv)
The point identified by the coordinates (2, −4).
🟢 Answer
✔️ Final: G
🔵 Question 2(v)
The abscissa of the point D.
🟢 Answer
🔵 Step 1: D lies on the positive x-axis at x = 6.
✔️ Final: 6
🔵 Question 2(vi)
The ordinate of the point H.
🟢 Answer
🔵 Step 1: H lies at y = −3.
✔️ Final: −3
🔵 Question 2(vii)
The coordinates of the point L.
🟢 Answer
✔️ Final: (0, 5)
🔵 Question 2(viii)
The coordinates of the point M.
🟢 Answer
✔️ Final: (−3, 0)
———————————————————————————————————————————————————————————————————————————–
OTHER IMPORTANT QUESTIONS FOR EXAMS
CBSE MODEL QUESTION PAPER
🔵 Question 1 (Section A)
Name the horizontal and vertical lines in the Cartesian plane.
🟢 Answer:
✳️ Horizontal line → x-axis
✳️ Vertical line → y-axis
🔵 Question 2 (Section A)
What is the point of intersection of the x-axis and y-axis called?
🟢 Answer:
✳️ The origin (denoted by O (0, 0))
🔵 Question 3 (Section A)
In which quadrant does (−3, 5) lie?
🟢 Answer:
✳️ x < 0, y > 0 → Quadrant II
🔵 Question 4 (Section A)
Give the coordinates of a point on the y-axis at 4 units above the origin.
🟢 Answer:
✳️ On y-axis: x = 0. So coordinates are (0, 4)
🔵 Question 5 (Section A)
State the sign of x and y in Quadrant III.
🟢 Answer:
✳️ Quadrant III: x < 0, y < 0 (both negative)
🔵 Question 6 (Section A)
If a point is equidistant from the axes, what can you say about its coordinates?
🟢 Answer:
✳️ |x| = |y| (absolute values equal)
🟡 Section B — Short Answer-I (2 marks each)
🔵 Question 7
Plot A(2, 3) and B(−1, 3) on a Cartesian plane. What is the distance between them?
🟢 Answer:
✳️ Points lie on a horizontal line (same y).
✳️ ➤ Formula: Distance = |x₂ − x₁|
✳️ ➤ Substitution: = |−1 − 2| = |−3| = 3 units
🔵 Question 8
Find the distance between P(0, 5) and Q(0, −3).
🟢 Answer:
✳️ Same x ⇒ vertical line.
✳️ ➤ Distance = |y₂ − y₁| = |−3 − 5| = |−8| = 8 units
🔵 Question 9
Find the midpoint of the segment joining (4, −2) and (−6, 5).
🟢 Answer:
✳️ ➤ Formula: M = ((x₁+x₂)/2, (y₁+y₂)/2)
✳️ ➤ Substitution: ((4 + (−6))/2, (−2 + 5)/2)
✳️ ➤ Simplification: ((−2)/2, 3/2) = (−1, 1.5)
🔵 Question 10
Determine the coordinates of a point R on the x-axis which is equidistant from P(−3, 2) and Q(5, 2).
🟢 Answer:
✳️ For R(x, 0): Distances PR = QR.
✳️ PR² = (x+3)² + (0−2)² = (x+3)² + 4
✳️ QR² = (x−5)² + (0−2)² = (x−5)² + 4
✳️ Equate: (x+3)² + 4 = (x−5)² + 4 ⇒ (x+3)² = (x−5)²
✳️ Expand: x² + 6x + 9 = x² −10x +25
✳️ Simplify: 6x + 9 = −10x +25 ⇒16x =16 ⇒x=1
✔️ R = (1, 0)
🔵 Question 11
Find the slope of the line joining A(−2, 1) and B(3, 4).
🟢 Answer:
✳️ ➤ Formula: m = (y₂ − y₁)/(x₂ − x₁)
✳️ ➤ Substitution: (4 −1)/(3 −(−2)) = 3/5
✔️ Slope = 3/5
🔵 Question 12
The point S divides the line segment joining A(−4, 2) and B(6, 8) in the ratio 2:3. Find the coordinates of S.
🟢 Answer:
✳️ ➤ Formula: S(x,y) = ( (m₂x₁ + m₁x₂)/(m₁+m₂), (m₂y₁ + m₁y₂)/(m₁+m₂) ) where m₁:m₂ =2:3.
✳️ ➤ Substitution: = ( (3×(−4) + 2×6)/(5), (3×2 + 2×8)/(5) )
✳️ ➤ Simplification: ( (−12 +12)/5, (6+16)/5 ) = (0/5,22/5 )
✔️ Coordinates of S = (0, 22/5) = (0, 4.4)
🔵 Question 13 (Section C)
Plot points A(2, 3), B(−2, 3), and C(2, −3). Join them. What figure is formed?
🟢 Answer:
✳️ Plot A(2, 3) and B(−2, 3) → horizontal line at y = 3.
✳️ Plot C(2, −3) → below A. Join to form right-angled figure.
✳️ AB = |2 − (−2)| = 4. AC = |3 − (−3)| = 6. BC diagonal.
✔️ Figure formed: Right-angled triangle at A.
🔵 Question 14 (Section C)
Find the distance between points (−4, −3) and (3, 5).
🟢 Answer:
✳️ ➤ Formula: d = √((x₂ − x₁)² + (y₂ − y₁)²)
✳️ ➤ Substitution: √((3 + 4)² + (5 + 3)²) = √(7² + 8²)
✳️ ➤ Simplification: √(49 + 64) = √113
✔️ Final answer: √113 units
🔵 Question 15 (Section C)
Find the coordinates of the centroid of the triangle with vertices P(−1, 3), Q(5, −7), and R(2, 6).
🟢 Answer:
✳️ ➤ Formula: Centroid G(x, y) = ((x₁+x₂+x₃)/3, (y₁+y₂+y₃)/3)
✳️ ➤ Substitution: ((−1 + 5 + 2)/3, (3 −7 + 6)/3) = (6/3, 2/3)
✔️ Centroid: (2, 2/3)
🔵 Question 16 (Section C)
Find the ratio in which the line segment joining A(−2, −3) and B(3, 7) is divided by the x-axis.
🟢 Answer:
✳️ For point P(x, 0) dividing AB in m:1, use section formula for y-coordinate:
0 = (m·7 + 1·(−3))/(m+1)
m·7 − 3 = 0 ⇒7m = 3 ⇒m = 3/7.
✔️ Ratio: 3:7
OR
🔵 Alternative Question 16
Find the ratio in which (−1, y) divides the segment joining (−3, −2) and (2, 3) if y = 0.
🟢 Answer (Alternative):
✳️ Using section formula for y: 0 = (m·3 + (−2))/(m+1) ⇒3m − 2 = 0 ⇒ m = 2/3.
✔️ Ratio: 2:3
🔵 Question 17 (Section C)
Find the coordinates of the point which divides the line joining (−1, 7) and (4, −3) in the ratio 2:3.
🟢 Answer:
✳️ ➤ Formula: ((m₂x₁ + m₁x₂)/(m₁+m₂), (m₂y₁ + m₁y₂)/(m₁+m₂)) with m₁:m₂ = 2:3.
✳️ ➤ Substitution: ((3×(−1)+2×4)/5, (3×7+2×(−3))/5)
✳️ ➤ Simplification: ((−3+8)/5, (21−6)/5) = (5/5,15/5) = (1,3).
✔️ Coordinates: (1, 3)
🔵 Question 18 (Section C)
The points A(1, 1), B(5, 1), C(3, 4) form a triangle. Find its area using the coordinate method.
🟢 Answer:
✳️ ➤ Formula: Area = ½|x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂)|
✳️ ➤ Substitution: = ½|1(1−4) + 5(4−1) + 3(1−1)|
✳️ ➤ Simplify: = ½|(−3) + 15 + 0| = ½|12| = 6.
✔️ Area: 6 square units
🔵 Question 19 (Section C)
Verify whether the points P(7, 10), Q(−2, 5), and R(3, −4) are collinear.
🟢 Answer:
✳️ Find slopes PQ and QR.
m₁ = (5 −10)/(−2 −7) = (−5)/(−9) = 5/9.
m₂ = (−4 −5)/(3 +2) = (−9)/5 = −9/5.
✳️ Since m₁ ≠ m₂, points are not collinear.
🔵 Question 20 (Section C)
Find the slope of the line passing through points (−3, −7) and (5, −7).
🟢 Answer:
✳️ ➤ Formula: m = (y₂ − y₁)/(x₂ − x₁) = (−7 +7)/(5 +3) = 0/8 = 0.
✔️ Slope: 0 (horizontal line)
🔵 Question 21 (Section C)
The vertices of a quadrilateral are A(0, 0), B(4, 0), C(4, 3), and D(0, 3). Find its area.
🟢 Answer:
✳️ It’s a rectangle: length = AB = 4, breadth = AD = 3.
✳️ Area = length × breadth = 4 × 3 = 12 square units
OR
🔵 Alternative Question 21
Find the perimeter of ΔABC with vertices A(−2, −3), B(3, 2), and C(−1, −8).
🟢 Answer (Alternative):
✳️ AB = √((3 +2)² + (2 +3)²) = √(25 +25) = √50 = 5√2.
✳️ BC = √((−1−3)² + (−8−2)²) = √((−4)² + (−10)²) = √(16 +100) = √116.
✳️ CA = √((−2 +1)² + (−3 +8)²) = √((−1)² +5²) = √26.
✳️ Perimeter ≈ 5√2 + √116 + √26.
🔵 Question 22 (Section C)
Find the coordinates of the point of trisection of the segment joining P(2, −2) and Q(8, 4) closer to P.
🟢 Answer:
✳️ Trisection divides PQ into three equal parts. Use section formula in ratio 1:2.
✳️ x = (2×2 +1×8)/3 = (4 +8)/3 =12/3=4.
✳️ y = (2×(−2)+1×4)/3 = (−4 +4)/3=0.
✔️ Point of trisection closer to P: (4, 0)
🔵 Question 23 (Section D)
Show that △ABC with A(1, 2), B(5, 6), C(1, 6) is a right isosceles triangle. Also find its perimeter.
🟢 Answer:
✳️ ➤ Formula: d = √((x₂ − x₁)² + (y₂ − y₁)²)
✳️ ➤ AB = √((5 − 1)² + (6 − 2)²) = √(4² + 4²) = √32 = 4√2
✳️ ➤ AC = √((1 − 1)² + (6 − 2)²) = √(0² + 4²) = 4
✳️ ➤ BC = √((1 − 5)² + (6 − 6)²) = √(−4)² = 4
✳️ ➤ Right angle at C (vector check): CA = (0, −4), CB = (4, 0) ⇒ CA·CB = 0 ⇒ ∠C = 90°
✳️ ➤ Isosceles: AC = BC = 4
✔️ Final: Right isosceles at C; Perimeter = 4√2 + 4 + 4 = 8 + 4√2 units
🔵 Question 24 (Section D)
Find k so that A(2, 3), B(4, k), C(6, 9) are collinear.
🟢 Answer:
✳️ ➤ Equal slopes: (k − 3)/(4 − 2) = (9 − k)/(6 − 4)
✳️ ➤ (k − 3)/2 = (9 − k)/2 ⇒ k − 3 = 9 − k ⇒ 2k = 12
✔️ Final: k = 6
OR
🔵 Alternative Question 24
If area of △ABC with A(−1, 3), B(5, 1), C(k, −2) is 9, find k.
🟢 Answer (Alt):
✳️ ➤ Area = ½ | x₁(y₂ − y₃) + x₂(y₃ − y₁) + x₃(y₁ − y₂) |
✳️ ➤ = ½ | (−1)(1 − (−2)) + 5(−2 − 3) + k(3 − 1) |
✳️ ➤ = ½ | (−1)·3 + 5·(−5) + 2k | = ½ | 2k − 28 |
✳️ ➤ ½ |2k − 28| = 9 ⇒ |k − 14| = 9 ⇒ k = 23 or 5
✔️ Final (Alt): k = 23 or k = 5
🔵 Question 25 (Section D)
Find the point that divides P(−2, 3) and Q(4, −1): (i) internally in 3:2, (ii) externally in 3:2.
🟢 Answer:
✳️ ➤ Internal section (m₁:m₂ = 3:2):
x = (m₂x₁ + m₁x₂)/(m₁ + m₂) = (2·(−2) + 3·4)/5 = 8/5
y = (m₂y₁ + m₁y₂)/(m₁ + m₂) = (2·3 + 3·(−1))/5 = 3/5
✳️ ➤ External section (m₁:m₂ = 3:2):
x = (m₂x₁ − m₁x₂)/(m₂ − m₁) = (2·(−2) − 3·4)/(2 − 3) = 16
y = (m₂y₁ − m₁y₂)/(m₂ − m₁) = (2·3 − 3·(−1))/(2 − 3) = −9
✔️ Final: Internal point (8/5, 3/5); External point (16, −9)
🔵 Question 26 (Section D)
In parallelogram ABCD, A(1, 2), B(4, 3), C(6, 7). Find the coordinates of D.
🟢 Answer:
✳️ ➤ Property (diagonals bisect): A + C = B + D ⇒ D = A + C − B
✳️ ➤ D = (1 + 6 − 4, 2 + 7 − 3) = (3, 6)
✔️ Final: D = (3, 6)
OR
🔵 Alternative Question 26
Verify that diagonals bisect and find the common midpoint.
🟢 Answer (Alt):
✳️ ➤ Midpoint of AC: M₁ = ( (1 + 6)/2 , (2 + 7)/2 ) = (3.5, 4.5)
✳️ ➤ With D = (3, 6), midpoint of BD: M₂ = ( (4 + 3)/2 , (3 + 6)/2 ) = (3.5, 4.5)
✔️ Final (Alt): M₁ = M₂ = (3.5, 4.5) (bisected)
🔵 Question 27 (Section D)
Find the centroid G of △ABC with A(−1, 4), B(5, −2), C(3, 6). Show that G lies on each median.
🟢 Answer:
✳️ ➤ Centroid: G = ( (x₁ + x₂ + x₃)/3 , (y₁ + y₂ + y₃)/3 )
✳️ ➤ G = ( (−1 + 5 + 3)/3 , (4 − 2 + 6)/3 ) = (7/3, 8/3)
✳️ ➤ Midpoint of BC: M_{BC} = ( (5 + 3)/2 , (−2 + 6)/2 ) = (4, 2)
✳️ ➤ Slope AG = ( (8/3 − 4) / (7/3 − (−1)) ) = ( (8/3 − 12/3) / (7/3 + 3/3) ) = (−4/3)/(10/3) = −2/5
✳️ ➤ Slope AM = (2 − 4)/(4 − (−1)) = −2/5
✔️ Final: G = (7/3, 8/3) and G lies on each median
🔵 Question 28 (Section D)
Find the area of quadrilateral A(−1, −1), B(3, 0), C(2, 4), D(−2, 3) using the Shoelace formula.
🟢 Answer:
✳️ ➤ Area = ½ | x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁ − (y₁x₂ + y₂x₃ + y₃x₄ + y₄x₁) |
✳️ ➤ Sum₁ = (−1·0) + (3·4) + (2·3) + (−2·−1) = 0 + 12 + 6 + 2 = 20
✳️ ➤ Sum₂ = (−1·3) + (0·2) + (4·−2) + (3·−1) = −3 + 0 − 8 − 3 = −14
✳️ ➤ Area = ½ |20 − (−14)| = ½ · 34 = 17
✔️ Final: 17 square units
OR
🔵 Alternative Question 28
Find the area of △PQR with P(0, 0), Q(a, 0), R(0, b).
🟢 Answer (Alt):
✳️ ➤ Right triangle on axes: Area = ½ × base × height
✳️ ➤ Area = ½ × a × b
✔️ Final (Alt): ab/2 square units
🔵 Question 29 (Section D)
Find the point P on the x-axis that minimises PA + PB, where A(2, 5) and B(−4, 1). (Hint: reflection.)
🟢 Answer:
✳️ ➤ Reflect A across x-axis: A′(2, −5).
✳️ ➤ Line A′B has slope m = (1 − (−5))/(−4 − 2) = 6/(−6) = −1.
✳️ ➤ Equation through A′(2, −5): y + 5 = −1(x − 2) ⇒ y = −x − 3.
✳️ ➤ Intersection with x-axis (y = 0): 0 = −x − 3 ⇒ x = −3.
✔️ Final: P = (−3, 0)
🔵 Question 30 (Section D)
Verify that A(1, 2), B(6, 2), C(6, 7), D(1, 7) form a rectangle and find its area.
🟢 Answer:
✳️ ➤ Slopes:
AB: (2 − 2)/(6 − 1) = 0 (horizontal),
BC: (7 − 2)/(6 − 6) → undefined (vertical),
CD: (7 − 7)/(1 − 6) = 0 (horizontal),
DA: (2 − 7)/(1 − 1) → undefined (vertical).
✳️ ➤ Opposite sides parallel; adjacent sides perpendicular ⇒ rectangle.
✳️ ➤ Length = AB = 6 − 1 = 5; Breadth = AD = 7 − 2 = 5.
✔️ Final: Rectangle; Area = 5 × 5 = 25 square units
————————————————————————————————————————————————————————————————————————————
MIND MAP
————————————————————————————————————————————————————————————————————————————
