Class : 9 – Math (Hindi) : Lesson 12. सांख्यिकी

पाठ का विश्लेषण  एवं  विवेचन

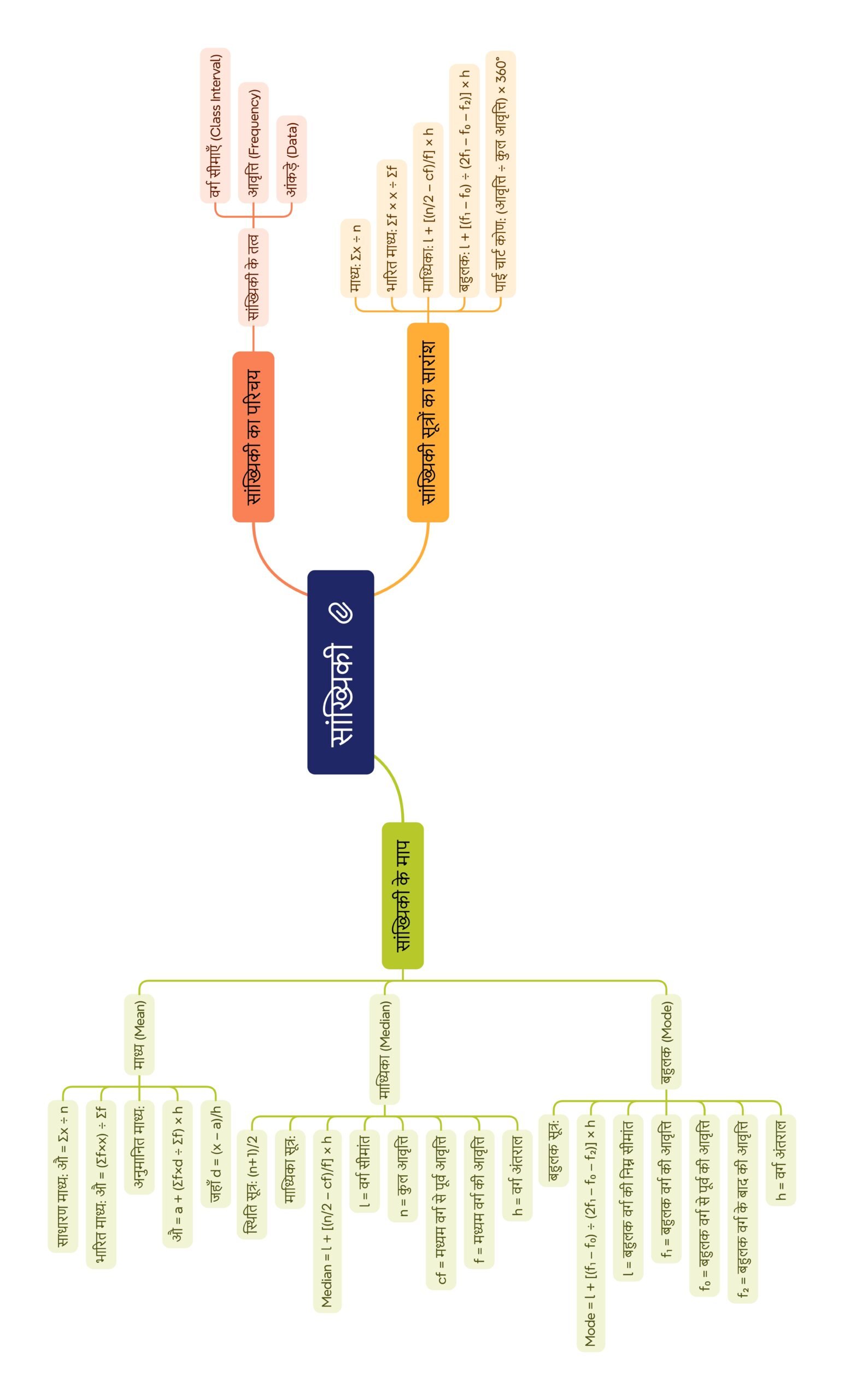
✨ विस्तृत व्याख्या
🔵 भूमिका
गणित का एक महत्त्वपूर्ण अंग है सांख्यिकी (Statistics)। यह विषय हमें आँकड़ों का संग्रह, वर्गीकरण, प्रस्तुतीकरण और विश्लेषण करना सिखाता है। वास्तविक जीवन में हमें बहुत-से आँकड़े मिलते हैं—जैसे विद्यार्थियों के अंक, किसी स्थान की जनसंख्या, क्रिकेट में बनाए गए रन, तापमान का दैनिक रिकार्ड इत्यादि। इन आँकड़ों को सरल और समझने योग्य रूप में प्रस्तुत करना तथा उनसे उपयोगी निष्कर्ष निकालना ही सांख्यिकी का उद्देश्य है।

🟢 सांख्यिकी की परिभाषा
सांख्यिकी वह गणितीय विधा है जिसके द्वारा हम आँकड़ों का संग्रह, वर्गीकरण, प्रस्तुतीकरण, विश्लेषण और निष्कर्ष निकालते हैं।
✏️ Note: आँकड़े (Data) किसी विशेष घटना या प्रयोग से संबंधित प्रेक्षण (observations) का समूह होते हैं।

🔴 आँकड़ों के प्रकार
कच्चे आँकड़े (Raw Data): सीधे प्रयोग या सर्वेक्षण से प्राप्त आँकड़े।
समूहीकृत आँकड़े (Grouped Data): जब आँकड़ों को वर्गों (classes) में बाँट दिया जाता है।
असमूहीकृत आँकड़े (Ungrouped Data): जब आँकड़ों को केवल सूचीबद्ध कर दिया जाए, जैसे 10 छात्रों के अंक।

🟡 आँकड़ों का संग्रहण
प्राथमिक आँकड़े (Primary Data): जो आँकड़े स्वयं एकत्रित किए जाएँ।
द्वितीयक आँकड़े (Secondary Data): जो आँकड़े किसी अन्य स्रोत (पुस्तक, पत्रिका, रिपोर्ट) से लिए जाएँ।

🔵 आँकड़ों का प्रस्तुतीकरण (Presentation of Data)
सारणीबद्ध प्रस्तुतीकरण (Tabular Presentation): आँकड़ों को सारणी (table) के रूप में प्रस्तुत करना।
आरेखीय प्रस्तुतीकरण (Graphical Presentation): आँकड़ों को चित्र या आरेख से दिखाना।

🟢 आलेख और आरेख
बार आलेख (Bar Graph):
आयताकार बार से आँकड़े दिखाना।
लंबाई या ऊँचाई आँकड़े का मान बताती है।
हिस्टोग्राम (Histogram):
समूहीकृत आँकड़ों को निरंतर वर्गों में बाँटकर बने आयत।
प्रत्येक आयत की चौड़ाई वर्गांतर और ऊँचाई आवृत्ति को दर्शाती है।
आवृत्ति बहुभुज (Frequency Polygon):
हिस्टोग्राम के मध्य बिंदुओं को जोड़कर बना हुआ बहुभुज।
💡 Concept: आँकड़ों का दृश्य रूप उन्हें समझने और तुलना करने में आसान बनाता है।

🔴 सांख्यिकीय माप (Measures of Central Tendency)
गणितीय औसत (Mean):
असमुहीकृत आँकड़े: Mean = (सभी प्रेक्षणों का योग) / (प्रेक्षणों की संख्या)
समूहीकृत आँकड़े: Mean = (Σfi xi) / (Σfi)
माध्यिका (Median):
आँकड़ों को आरोही/अवरोही क्रम में रखने पर बीच का मान।
यदि n विषम है → माध्यिका = (n+1)/2वाँ प्रेक्षण।
यदि n सम है → माध्यिका = (n/2वाँ प्रेक्षण + (n/2 + 1)वाँ प्रेक्षण)/2
बहुलक (Mode):
वह मान जो आँकड़ों में सर्वाधिक बार आता है।
✏️ Note: माध्य, माध्यिका और बहुलक को “केंद्रीय प्रवृत्ति के माप” कहते हैं।

🟡 उदाहरण
उदाहरण 1:
10 विद्यार्थियों के अंक: 5, 7, 10, 8, 9, 6, 7, 10, 8, 7
गणितीय औसत = (5+7+10+8+9+6+7+10+8+7)/10 = 77/10 = 7.7
माध्यिका = मध्य मान = 7.5
बहुलक = 7 (सबसे अधिक बार आने वाला अंक)

🔵 वास्तविक जीवन के अनुप्रयोग
विद्यालय में अंकों का विश्लेषण।
मौसम विभाग में तापमान का औसत निकालना।
खेलों में खिलाड़ियों के प्रदर्शन की तुलना।
व्यवसाय और अर्थशास्त्र में उत्पादन व बिक्री का अध्ययन।

🟢 अध्याय का महत्व
आँकड़ों को व्यवस्थित रूप से प्रस्तुत और समझने की क्षमता।
निर्णय लेने में मददगार।
आगे की कक्षाओं में प्रायिकता, अर्थशास्त्र और अनुसंधान विषयों के लिए आधार तैयार करता है।

📌 Summary
सांख्यिकी: आँकड़ों का संग्रह, वर्गीकरण, प्रस्तुतीकरण और विश्लेषण।
प्रकार: कच्चे आँकड़े, समूहीकृत, असमुहीकृत।
संग्रहण: प्राथमिक और द्वितीयक।
प्रस्तुतीकरण: सारणी, बार आलेख, हिस्टोग्राम, आवृत्ति बहुभुज।
माप:
औसत (Mean) = Σxi / n या Σfi xi / Σfi
माध्यिका (Median) = बीच का मान
बहुलक (Mode) = सबसे अधिक बार आने वाला मान
अनुप्रयोग: शिक्षा, मौसम, खेल, अर्थशास्त्र।
महत्व: आँकड़ों का विश्लेषण कर उपयोगी निष्कर्ष निकालना।

📝 Quick Recap
🔵 सांख्यिकी = आँकड़ों का अध्ययन।
🟢 केंद्रीय प्रवृत्ति = औसत, माध्यिका, बहुलक।
🟡 प्रस्तुतीकरण = बार आलेख, हिस्टोग्राम, बहुभुज।
🔴 अनुप्रयोग = शिक्षा, खेल, मौसम, व्यवसाय।

————————————————————————————————————————————————————————————————————————————

पाठ्यपुस्तक के प्रश्न

प्रश्नावली 12.1

🔵 प्रश्न 1.
एक संगठन ने पूरे विश्व में 15–44 (वर्ष में) की आयु वाली महिलाओं में बीमारी और मृत्यु के कारणों का पता लगाने के लिए किए गए सर्वेक्षण से निम्नलिखित आँकड़े (% में) प्राप्त किए :
(i) ऊपर दी गई सूचनाओं का आलेखीय रूप में निरूपण कीजिए।
(ii) कौन-सी अवस्था पूरे विश्व की महिलाओं के खराब स्वास्थ्य और मृत्यु का बड़ा कारण है?
(iii) अपनी अध्यापिका की सहायता से ऐसे दो कारणों का पता लगाइए जिनकी (i) में मुख्य भूमिका रहती हो।
🟢 उत्तर:
(i) आलेख (स्तंभीय आरेख) बनाने की विधि — step-by-step
➡️ क्षैतिज अक्ष (x-axis) पर “कारण” रखें और ऊर्ध्वाधर अक्ष (y-axis) पर “महिला मृत्यु दर (%)” रखें।
➡️ y-axis का पैमाना चुनें (उदा., 0, 5, 10, …, 35)।
➡️ तालिका में दिए प्रत्येक कारण के लिए संबंधित प्रतिशत जितनी ऊँचाई का स्तम्भ खींचें।
➡️ प्रत्येक स्तम्भ के नीचे कारण का नाम लिखें; ऊपर शिखर पर प्रतिशत अंकित करें।
➡️ शीर्षक: “15–44 वर्ष की महिलाओं में मृत्यु के प्रमुख कारण (%)”.
(टिप: यही आँकड़े वृत्त-चित्र से भी दिखाए जा सकते हैं; तब हर कारण का केंद्रीय कोण = (प्रतिशत ÷ 100) × 360° होगा।)
(ii) सबसे बड़ा कारण (तालिका के अधिकतम % से):
➡️ अधिकतम प्रतिशत = 31.8% → कारण: जन्म स्वास्थ्य अवस्था।
✔️ निष्कर्ष: “जन्म स्वास्थ्य अवस्था” सबसे बड़ा कारण है।
(iii) स्थानीय स्तर पर दो संभावित प्रमुख कारण (उदाहरण):
➡️ प्रसूति/पूर्व-प्रसूति देखभाल का अभाव, कुपोषण।
➡️ समय पर चिकित्सकीय सुविधा/परिवहन का अभाव।
(नोट: यह भाग संदर्भ-आधारित उत्तर है; अपनी कक्षा/समुदाय की जानकारी के अनुसार दो कारण लिखें।)

🔵 प्रश्न 2.
भारतीय समाज के विभिन्न क्षेत्रों में प्रति हजार लड़कों पर लड़कियों की (नवजात तक की) संख्या के आँकड़े नीचे दिए गए हैं :
क्षेत्र — प्रति हजार लड़कों पर लड़कियों की संख्या
• अनुसूचित जाति — 940
• अनुसूचित जनजाति — 970
• गैर अनुसूचित जाति/जनजाति — 950
• पिछड़े जिले — 950
• गैर पिछड़े जिले — 920
• ग्रामीण — 930
• शहरी — 910
(i) ऊपर दी गई सूचनाओं का एक स्तंभीय आरेख (bar graph) बनाइए।
(ii) किन क्षेत्रों में, लड़कों के मुक़ाबले, लड़कियों की संख्या सबसे कम है?
(iii) किन क्षेत्रों में सबसे अधिक है?
🟢 उत्तर:
(i) स्तंभीय आरेख — step-by-step
➡️ x-axis पर “क्षेत्र” और y-axis पर “प्रति 1000 लड़कों पर लड़कियाँ” रखें।
➡️ y-axis पैमाना चुनें (उदा., 900, 910, 920, …, 980)।
➡️ हर क्षेत्र के लिए दिए गए मान (ऊपर सूची) के बराबर ऊँचाई का स्तम्भ खींचें।
➡️ शीर्षक: “भारत में विभिन्न क्षेत्रों में प्रति 1000 लड़कों पर लड़कियाँ”.
(ii) सबसे कम संख्या (न्यूनतम मान):
➡️ न्यूनतम = 910 → शहरी क्षेत्र।
✔️ निष्कर्ष: शहरी क्षेत्र में लड़कियों की संख्या सबसे कम है।
(iii) सबसे अधिक संख्या (अधिकतम मान):
➡️ अधिकतम = 970 → अनुसूचित जनजाति।
✔️ निष्कर्ष: अनुसूचित जनजाति में लड़कियों की संख्या सबसे अधिक है।

🔵 प्रश्न 3.
एक राज्य के विधान सभा के चुनाव में विभिन्न राजनीतिक पार्टियों द्वारा जीती गई सीटों के परिणाम नीचे दिए गए हैं :
राजनीतिक पार्टी : A, B, C, D, E, F
जीती गई सीटें : 75, 55, 37, 29, 10, 37
(i) मतदान के परिणामों को निरूपित करने वाला एक वृत्त आलेख (pie chart) खींचिए।
(ii) किस राजनीतिक पार्टी ने अधिकतम सीटें जीतीं हैं?
🟢 उत्तर:
(i) वृत्त आलेख बनाने की विधि
➡️ कुल सीटें = 75 + 55 + 37 + 29 + 10 + 37 = 243
➡️ प्रत्येक पार्टी का कोण = (जीती गई सीटें ÷ 243) × 360°
पार्टी A: (75/243) × 360° ≈ 111°
पार्टी B: (55/243) × 360° ≈ 82°
पार्टी C: (37/243) × 360° ≈ 55°
पार्टी D: (29/243) × 360° ≈ 43°
पार्टी E: (10/243) × 360° ≈ 15°
पार्टी F: (37/243) × 360° ≈ 54°
➡️ वृत्त को 6 क्षेत्रों में बाँटकर उपरोक्त कोणों के अनुसार आरेखित करें।
(ii) अधिकतम सीटें = 75 (पार्टी A)
✔️ उत्तर: पार्टी A ने सबसे अधिक सीटें जीतीं।

🔵 प्रश्न 4.
एक पेपर फैक्ट्री की 40 पत्तियों की लंबाई (एक मिलीमीटर तक शुद्ध मापी गई) के आँकड़े दिए गए :
लंबाई (मिमी) : 118–126, 127–135, 136–144, 145–153, 154–162, 163–171, 172–180
पत्तियों की संख्या : 3, 5, 9, 12, 5, 4, 2
(i) दिए हुए आँकड़ों को निरूपित करने वाला एक आयतचित्र (histogram) खींचिए।
(ii) क्या इन्हीं आँकड़ों को निरूपित करने वाला कोई अन्य उपयुक्त आलेख है?
(iii) क्या यह सही निष्कर्ष है कि 153 मिमी लंबाई वाली पत्तियों की संख्या सबसे अधिक है? क्यों?
🟢 उत्तर:
(i) आयतचित्र की विधि
➡️ x-axis पर “लंबाई (मिमी)” को वर्ग अंतरालों में रखें।
➡️ y-axis पर “पत्तियों की संख्या” रखें।
➡️ प्रत्येक वर्ग-अंतराल के लिए उसकी संख्या (frequency) के बराबर ऊँचाई के आयत खींचें।
(ii) इन आँकड़ों को आवृत्ति बहुभुज (frequency polygon) और आवृत्ति वक्र द्वारा भी निरूपित किया जा सकता है।
(iii) नहीं। यहाँ 145–153 मिमी वर्ग में 12 पत्तियाँ हैं, परन्तु इसका मतलब यह नहीं कि ठीक 153 मिमी वाली पत्तियाँ सबसे अधिक हैं। यह आँकड़े समूहित रूप में दिए गए हैं। इसलिए सही निष्कर्ष होगा: 145–153 मिमी वर्ग में सबसे अधिक पत्तियाँ पाई गईं।
✔️ उत्तर: सबसे अधिक पत्तियाँ 145–153 मिमी वर्ग-अंतराल में हैं, न कि केवल 153 मिमी पर।

🔵 प्रश्न 5.
नीचे की सारणी में 400 नियॉन लैंपों के जीवन काल (घंटों में) दिए गए हैं :
जीवन काल (घंटों में): 300–400, 400–500, 500–600, 600–700, 700–800, 800–900, 900–1000
लैंपों की संख्या: 14, 56, 60, 86, 74, 62, 48
(i) एक आयतचित्र की सहायता से दी हुई सूचनाओं को निरूपित कीजिए।
(ii) कितने लैंपों के जीवन काल 700 घंटों से अधिक हैं?
🟢 उत्तर:
(i) आयतचित्र बनाने की विधि
➡️ x-axis पर जीवन काल के वर्ग अंतराल लें।
➡️ y-axis पर लैंपों की संख्या लें।
➡️ प्रत्येक वर्ग अंतराल के लिए दिए गए मान के अनुसार आयत खींचें।
(ii) 700 घंटों से अधिक जीवन काल वाले वर्ग:
700–800 = 74
800–900 = 62
900–1000 = 48
कुल = 74 + 62 + 48 = 184 लैंप
✔️ उत्तर: 184 लैंपों का जीवन काल 700 घंटों से अधिक है।

🔵 प्रश्न 6.
नीचे की दो सारणियों में प्राप्त किए गए अंकों के अनुसार दो सेक्शनों के विद्यार्थियों का वितरण दिया गया है :
सेक्शन A (बारंबारता): 3, 9, 17, 12, 9
सेक्शन B (बारंबारता): 5, 19, 15, 1, 1
दो बारंबारता बहुभुज की सहायता से एक ही आलेख पर दोनों सेक्शनों के विद्यार्थियों के प्राप्तांक निरूपित कीजिए। दोनों बहुभुज का अध्ययन करके दोनों सेक्शनों के विद्यार्थियों की उपलब्धियों की तुलना कीजिए।
🟢 उत्तर:
(i) बहुभुज (Frequency Polygon) बनाने की विधि
➡️ x-axis पर “अंक” (class intervals: 0–10, 10–20, 20–30, 30–40, 40–50) रखें।
➡️ y-axis पर “बारंबारता” रखें।
➡️ सेक्शन A के लिए बिंदु अंकित करें: (5,3), (15,9), (25,17), (35,12), (45,9)।
➡️ सेक्शन B के लिए बिंदु अंकित करें: (5,5), (15,19), (25,15), (35,1), (45,1)।
➡️ दोनों श्रृंखलाओं को रेखाओं से जोड़ें।
(ii) तुलना
✔️ सेक्शन B के 10–20 अंक वर्ग में सर्वाधिक विद्यार्थी (19) हैं।
✔️ सेक्शन A का वितरण अधिक संतुलित है, जबकि सेक्शन B में अधिकांश विद्यार्थी कम अंकों पर केंद्रित हैं।
✔️ निष्कर्ष: सेक्शन A का प्रदर्शन बेहतर और संतुलित है।

🔵 प्रश्न 7.
एक क्रिकेट मैच में दो टीमें A और B द्वारा 60 गेंदों में बनाए गए रन नीचे दिए गए हैं :
गेंदों की संख्या – टीम A (2,2,8,9,4,8,1,6,10,10)
गेंदों की संख्या – टीम B (5,1,6,10,6,6,2,3,1,10)
चार्ट (बारंबारता बहुभुज) की सहायता से एक ही आलेख पर दोनों टीमों के आँकड़े निरूपित कीजिए।
🟢 उत्तर:
(i) बहुभुज (Frequency Polygon) बनाने की विधि
➡️ x-axis पर वर्ग-अंतराल (गेंदों की संख्या): 1–6, 7–12, 13–18, …, 55–60।
➡️ y-axis पर आवृत्ति (बारंबारता) रखें।
➡️ टीम A के लिए बिंदु: (3,2), (9,2), (15,8), (21,9), (27,4), (33,8), (39,1), (45,6), (51,10), (57,10)।
➡️ टीम B के लिए बिंदु: (3,5), (9,1), (15,6), (21,10), (27,6), (33,6), (39,2), (45,3), (51,1), (57,10)।
➡️ दोनों सेटों को जोड़कर एक ही आलेख पर अंकित करें।
(ii) तुलना
✔️ टीम A ने अधिक निरंतरता से रन बनाए, कई वर्गों में अच्छे स्कोर हैं।
✔️ टीम B ने भी कुछ वर्गों (19–24 और 55–60) में ऊँचे स्कोर किए, पर बीच के वर्गों में असंतुलन है।
✔️ निष्कर्ष: टीम A का प्रदर्शन अधिक संतुलित रहा, टीम B का प्रदर्शन उतार-चढ़ाव वाला रहा।

————————————————————————————————————————————————————————————————————————————

अन्य महत्वपूर्ण प्रश्न

🔵 Section A (प्रत्येक 1 अंक, कुल 6 प्रश्न)
🔵 Question 1:
कच्चे आँकड़े (Raw Data) किसे कहते हैं?
🟢 Answer:
वे आँकड़े जो सीधे सर्वेक्षण या प्रयोग से बिना किसी वर्गीकरण के प्राप्त हों, कच्चे आँकड़े कहलाते हैं।

🔵 Question 2:
10 छात्रों के अंकों की सूची दी गई है: 5, 8, 6, 9, 7, 5, 10, 8, 9, 6।
बहुलक (Mode) ज्ञात कीजिए।
🟢 Answer:
सबसे अधिक बार आने वाला अंक = 5 और 6 और 8 तथा 9 (प्रत्येक 2 बार)
अतः बहुलक = 5, 6, 8, 9 (बहुलक एक से अधिक भी हो सकता है)।

🔵 Question 3:
सांख्यिकी का मुख्य उद्देश्य क्या है?
🟢 Answer:
आँकड़ों का सारणीकरण और उनका विश्लेषण करके उपयोगी निष्कर्ष निकालना।

🔵 Question 4:
यदि माध्य (Mean) = 12 और कुल प्रेक्षण = 10 हों, तो सभी प्रेक्षणों का योग ज्ञात कीजिए।
🟢 Answer:
योग = Mean × n = 12 × 10 = 120

🔵 Question 5:
आवृत्ति सारणी (Frequency Table) का क्या उपयोग है?
🟢 Answer:
बड़े आँकड़ों को व्यवस्थित कर उन्हें सरल और समझने योग्य बनाना।

🔵 Question 6 (MCQ):
यदि किसी डेटा का बहुलक 7 है, तो इसका अर्थ है:
1️⃣ सबसे छोटा मान 7 है।
2️⃣ सबसे बड़ा मान 7 है।
3️⃣ 7 सबसे अधिक बार आता है।
4️⃣ 7 औसत है।
🟢 Answer: 3️⃣

🟢 Section B (प्रत्येक 2 अंक, कुल 6 प्रश्न)
🔵 Question 7:
10 विद्यार्थियों के अंक: 12, 15, 10, 18, 20, 12, 17, 13, 16, 12।
गणितीय औसत (Mean) निकालिए।
🟢 Answer:
योग = 145
n = 10
Mean = 145/10 = 14.5

🔵 Question 8:
माध्यिका (Median) और बहुलक (Mode) में अंतर स्पष्ट कीजिए।
🟢 Answer:
माध्यिका = आँकड़ों को क्रम में रखने पर बीच का मान।
बहुलक = आँकड़ों में सबसे अधिक बार आने वाला मान।

🔵 Question 9:
किसी क्रिकेट खिलाड़ी ने 7 मैचों में बनाए रन: 25, 30, 15, 40, 35, 20, 45।
औसत रन ज्ञात कीजिए।
🟢 Answer:
योग = 210
n = 7
Mean = 210/7 = 30

🔵 Question 10:
एक सर्वेक्षण में 50 छात्रों से उनकी पसंदीदा खेल के बारे में पूछा गया। प्राप्त आँकड़े:
क्रिकेट = 20, फुटबॉल = 15, हॉकी = 10, बैडमिंटन = 5।
बार आलेख बनाने की विधि लिखिए।
🟢 Answer:
क्षैतिज अक्ष पर खेल और लंबवत अक्ष पर संख्या लिखें।
क्रिकेट (20), फुटबॉल (15), हॉकी (10), बैडमिंटन (5) के आयताकार बार बनाइए।

🔵 Question 11:
सारणीकरण (Tabulation) के लाभ लिखिए।
🟢 Answer:
आँकड़े सरल और सुव्यवस्थित बनते हैं।
तुलना करना आसान होता है।

🔵 Question 12 (Assertion–Reason):
कथन (A): बहुलक वह मान है जो सबसे अधिक बार आता है।
कारण (R): बहुलक हमेशा औसत से बड़ा होता है।
विकल्प:
A. कथन और कारण दोनों सही हैं।
B. कथन सही है, कारण गलत है।
C. कथन गलत है, कारण सही है।
D. दोनों गलत हैं।
🟢 Answer: B

🟡 Section C (प्रत्येक 3 अंक, कुल 10 प्रश्न, 3–4 में आंतरिक विकल्प)

🔵 Question 13:
किसी विद्यालय के 40 विद्यार्थियों की ऊँचाई (से.मी. में) का निम्नलिखित सारणीकरण दिया गया है:
| ऊँचाई (से.मी.) | 140–150 | 150–160 | 160–170 | 170–180 | 180–190 |
|—————-|———|———|———|———|
| संख्या | 5 | 12 | 14 | 6 | 3 |
औसत ऊँचाई (Mean) निकालिए।
🟢 Answer:
Mean = (Σfi xi)/(Σfi)
कक्षा मध्य = 145, 155, 165, 175, 185
Σfi = 40
Σfi xi = 5×145 + 12×155 + 14×165 + 6×175 + 3×185 = 6600
Mean = 6600 / 40 = 165 से.मी.

🔵 Question 14:
20 छात्रों के गणित के अंक इस प्रकार हैं:
12, 18, 15, 20, 22, 25, 18, 20, 24, 19, 16, 15, 14, 12, 22, 18, 20, 24, 25, 22।
माध्यिका (Median) ज्ञात कीजिए।
🟢 Answer:
क्रम में आँकड़े लिखें।
n = 20 (सम संख्या)
Median = (10वाँ + 11वाँ)/2 = (19 + 20)/2 = 19.5 अंक

🔵 Question 15 (आंतरिक विकल्प):
(A) निम्नलिखित आवृत्ति वितरण में बहुलक ज्ञात कीजिए:
| अंक | 0–10 | 10–20 | 20–30 | 30–40 | 40–50 |
|—–|——-|——–|——–|——–|
| f | 5 | 8 | 15 | 12 | 10 |
🟢 Answer:
बहुलक कक्षा = 20–30 (f₁=15, f₀=8, f₂=12)
L = 20, h = 10
Mode = L + [(f₁−f₀)/(2f₁−f₀−f₂)] × h
= 20 + [(15−8)/(30−8−12)] × 10
= 20 + (7/10)×10 = 27
Mode = 27
OR
(B) किसी आँकड़े में बहुलक 18 है, औसत 20 है। तो माध्यिका का मान ज्ञात कीजिए।
(सूत्र: Mode = 3Median − 2Mean)
Mode = 18, Mean = 20
18 = 3Median − 40
Median = 58/3 = 19.33

🔵 Question 16:
नीचे दी गई सारणी एक फैक्ट्री के 50 मजदूरों की दैनिक आय दर्शाती है:
| आय (रु. में) | 100–120 | 120–140 | 140–160 | 160–180 | 180–200 |
|————–|———|———|———|———|
| मजदूरों की संख्या | 8 | 12 | 20 | 6 | 4 |
इस आँकड़े का माध्यिका (Median) ज्ञात कीजिए।
🟢 Answer:
N = 50
Median class = 140–160
L = 140, N/2 = 25, cf = 20, f = 20, h = 20
Median = L + [(N/2 − cf)/f] × h
= 140 + [(25−20)/20] × 20 = 140 + 5 = 145

🔵 Question 17 (आंतरिक विकल्प):
(A) छात्रों के अंकों का औसत 50 है। यदि 30 छात्रों का कुल योग 1500 है, तो औसत सही सिद्ध कीजिए।
🟢 Answer:
Mean = Σx / n = 1500 / 30 = 50 (सही)
OR
(B) किसी डेटा में Mean = 25, Mode = 27 है। Median ज्ञात कीजिए।
Mode = 3Median − 2Mean
27 = 3Median − 50
3Median = 77
Median = 25.67

🔵 Question 18:
5 परिवारों की मासिक आय (हजार रु. में): 20, 22, 25, 18, 15।
औसत आय ज्ञात कीजिए और उसका अर्थ समझाइए।
🟢 Answer:
Σx = 100, n = 5
Mean = 100/5 = 20 हजार रु.
अर्थ: औसतन प्रत्येक परिवार की आय 20 हजार रु. है।

🔵 Question 19:
नीचे की सारणी में 60 छात्रों की ऊँचाई (से.मी. में) दी गई है। माध्यिका निकालिए।
| ऊँचाई | 140–150 | 150–160 | 160–170 | 170–180 | 180–190 |
|——–|———|———|———|———|
| संख्या | 5 | 15 | 20 | 12 | 8 |
🟢 Answer:
N = 60, N/2 = 30
Median class = 160–170
L = 160, cf = 20, f = 20, h = 10
Median = 160 + [(30−20)/20]×10 = 160 + 5 = 165 से.मी.

🔵 Question 20 (आंतरिक विकल्प):
(A) 100 मजदूरों की दैनिक आय का Mean 200 रु. है। यदि कुल आय = Σx = 20,000 है, तो औसत सही सिद्ध कीजिए।
🟢 Answer:
Mean = Σx / n = 20,000 / 100 = 200 (सही)
OR
(B) 20 छात्रों की औसत आयु 12 वर्ष है। यदि शिक्षक की आयु भी जोड़ दी जाए तो औसत 12.5 हो जाता है। शिक्षक की आयु ज्ञात कीजिए।
Σx = 20×12 = 240
नई औसत = (240 + x)/21 = 12.5
240 + x = 262.5
x = 22.5 वर्ष

🔵 Question 21:
समूहबद्ध आँकड़ों में औसत निकालने की “सरणी विधि” (Table Method) और “चरण विचलन विधि” (Step Deviation Method) में अंतर बताइए।
🟢 Answer:
सरणी विधि: xi और fi xi सीधे जोड़े जाते हैं।
चरण विचलन विधि: गणना को सरल करने के लिए (xi − A)/h का प्रयोग किया जाता है।
परिणाम समान, पर चरण विचलन विधि गणना आसान बनाती है।

🔵 Question 22:
नीचे दिए गए आँकड़ों में बहुलक (Mode) ज्ञात कीजिए:
| अंक | 0–10 | 10–20 | 20–30 | 30–40 | 40–50 |
|—–|——-|——–|——–|——–|
| f | 6 | 8 | 10 | 15 | 11 |
🟢 Answer:
Modal class = 30–40, L = 30, f₁ = 15, f₀ = 10, f₂ = 11, h = 10
Mode = 30 + [(15−10)/(2×15−10−11)] × 10
= 30 + (5/9)×10 = 30 + 5.56 = 35.56

🔴 Section D (प्रत्येक 4 अंक, कुल 8 प्रश्न, 3 में आंतरिक विकल्प)

🔵 Question 23:
निम्नलिखित सारणी से माध्य (Mean) निकालिए:
| वर्ग अंतराल | 0–10 | 10–20 | 20–30 | 30–40 | 40–50 |
|————-|——-|——–|——–|——–|
| आवृत्ति (f) | 5 | 7 | 10 | 8 | 5 |
🟢 Answer:
मध्य मान (xi) = 5, 15, 25, 35, 45
Σfi = 35
Σfixi = 5×5 + 7×15 + 10×25 + 8×35 + 5×45 = 875
Mean = 875 / 35 = 25 अंक

🔵 Question 24 (आंतरिक विकल्प):
(A) किसी 50 छात्रों की ऊँचाई (से.मी.) की माध्यिका निकालिए:
| ऊँचाई | 140–150 | 150–160 | 160–170 | 170–180 | 180–190 |
|——–|———|———|———|———|
| संख्या | 5 | 10 | 20 | 10 | 5 |
🟢 Answer:
N = 50, N/2 = 25
Median class = 160–170
L = 160, cf = 15, f = 20, h = 10
Median = 160 + [(25−15)/20]×10 = 165
OR
(B) किसी आँकड़े में Mean = 20, Mode = 22 है। Median ज्ञात कीजिए।
सूत्र: Mode = 3Median − 2Mean
22 = 3Median − 40
3Median = 62 → Median = 20.67

🔵 Question 25:
निम्नलिखित सारणी से बहुलक निकालिए:
| वर्ग अंतराल | 0–10 | 10–20 | 20–30 | 30–40 | 40–50 |
|————-|——-|——–|——–|——–|
| f | 4 | 9 | 15 | 10 | 2 |
🟢 Answer:
Modal class = 20–30
L = 20, h = 10, f₁=15, f₀=9, f₂=10
Mode = 20 + [(15−9)/(30−9−10)]×10
= 20 + (6/11)×10 = 25.45

🔵 Question 26 (आंतरिक विकल्प):
(A) किसी विद्यालय के 60 छात्रों की आयु इस प्रकार दी गई है। Mean निकालिए।
| आयु (वर्ष) | 10–12 | 12–14 | 14–16 | 16–18 | 18–20 |
|————|——–|——–|——–|——–|
| संख्या | 5 | 10 | 20 | 15 | 10 |
🟢 Answer:
xi = 11, 13, 15, 17, 19
Σfi = 60
Σfixi = 5×11 + 10×13 + 20×15 + 15×17 + 10×19 = 910
Mean = 910/60 = 15.17
OR
(B) 50 छात्रों का औसत अंक 35 है। यदि एक छात्र के अंक गलती से 45 की जगह 55 लिख दिए गए हों, तो सही औसत निकालिए।
गलत योग = 50×35 = 1750
सही योग = 1750 − 55 + 45 = 1740
Mean = 1740/50 = 34.8

🔵 Question 27:
समूहबद्ध आँकड़ों में Mean निकालने की तीन विधियाँ लिखकर उदाहरण सहित समझाइए।
🟢 Answer:
1️⃣ प्रत्यक्ष विधि: Mean = Σfixi/Σfi
2️⃣ विचलन विधि: Mean = A + Σfi di / Σfi (जहाँ di = xi − A)
3️⃣ चरण विचलन विधि: Mean = A + (Σfi ui / Σfi) × h (ui = (xi−A)/h)
✔️ तीनों से परिणाम समान मिलता है।

🔵 Question 28 (आंतरिक विकल्प):
(A) निम्नलिखित डेटा का माध्य निकालिए:
| वर्ग अंतराल | 0–10 | 10–20 | 20–30 | 30–40 | 40–50 |
|————-|——-|——–|——–|——–|
| f | 6 | 8 | 10 | 9 | 7 |
🟢 Answer:
xi = 5, 15, 25, 35, 45
Σfi = 40
Σfixi = 5×6 + 15×8 + 25×10 + 35×9 + 45×7 = 1060
Mean = 1060/40 = 26.5
OR
(B) किसी डेटा में Mean = 30, Median = 28 है। Mode ज्ञात कीजिए।
Mode = 3Median − 2Mean = 84 − 60 = 24

🔵 Question 29:
सांख्यिकी के महत्व पर 4 बिंदु लिखिए।
🟢 Answer:
आँकड़ों का सरल प्रस्तुतीकरण।
तुलना करना आसान।
निर्णय लेने में सहायक।
वैज्ञानिक अनुसंधान और नीतियों में उपयोगी।

🔵 Question 30 (आंतरिक विकल्प):
(A) 100 छात्रों के गणित के अंकों का औसत 40 है। कुल योग ज्ञात कीजिए।
🟢 Answer:
Σx = Mean × n = 40 × 100 = 4000
OR
(B) 20 छात्रों की औसत आयु 15 वर्ष है। यदि शिक्षक की आयु भी जोड़ दी जाए तो औसत 15.5 वर्ष हो जाता है। शिक्षक की आयु ज्ञात कीजिए।
Σx = 20×15 = 300
(300 + x)/21 = 15.5
300 + x = 325.5
x = 25.5 वर्ष

————————————————————————————————————————————————————————————————————————————

मानचित्र

————————————————————————————————————————————————————————————————————————————