Class : 9 – Math (Hindi) : Lesson 5. युक्लिड की ज्यामिति का परिचय

पाठ का विश्लेषण  एवं  विवेचन

✨ विस्तृत व्याख्या
🔵 भूमिका
युक्लिड की ज्यामिति गणित के इतिहास का एक अत्यंत महत्त्वपूर्ण अध्याय है। प्राचीन यूनान के गणितज्ञ युक्लिड (Euclid) ने लगभग 300 ईसा पूर्व ज्यामिति को एक व्यवस्थित रूप प्रदान किया। उसने अपनी पुस्तक एलिमेंट्स (Elements) में ज्यामिति के मूलभूत सिद्धांत, परिभाषाएँ और स्वयंसिद्ध प्रस्तुत किए। यही कारण है कि युक्लिड को “ज्यामिति का जनक” कहा जाता है।

🟢 परिभाषाएँ (Definitions)
युक्लिड ने अनेक आधारभूत परिभाषाएँ दीं। कुछ प्रमुख परिभाषाएँ:
🔵 बिंदु (Point): जिसका कोई आयाम नहीं होता।
🟢 रेखा (Line): लंबाई होती है, पर चौड़ाई नहीं।
🔴 सीधी रेखा (Straight Line): जो अपने दोनों सिरों के बीच समान रूप से फैली हो।
🟡 सतह (Surface): जिसकी केवल लंबाई और चौड़ाई हो।
🔵 समतल सतह (Plane Surface): जो अपने भीतर हर दिशा में समान रूप से हो।
✏️ Note: ये परिभाषाएँ हमें ज्यामितीय वस्तुओं को समझने का आधार देती हैं।

🔴 युक्लिड की ज्यामिति की संरचना
युक्लिड ने ज्यामिति को पाँच भागों में बाँटा:
परिभाषाएँ (Definitions)
सामान्य धारणाएँ (Common Notions/Axioms)
स्वयंसिद्ध (Postulates)
प्रमेय (Theorems)
प्रमाण (Proofs)
💡 Concept: गणित की विशेषता यह है कि हम मूलभूत स्वयंसिद्धों से जटिल प्रमेय सिद्ध कर सकते हैं।

🟡 सामान्य धारणाएँ (Common Notions)
युक्लिड ने कुछ सामान्य धारणाएँ दीं, जैसे:
यदि दो वस्तुएँ एक ही वस्तु के बराबर हों, तो वे आपस में भी बराबर होंगी।
यदि बराबर में बराबर जोड़े जाएँ, तो परिणाम भी बराबर होंगे।
यदि बराबर में बराबर घटाए जाएँ, तो शेष भी बराबर होंगे।
सम्पूर्ण अपने भागों से बड़ा होता है।
✔️ ये धारणाएँ केवल ज्यामिति ही नहीं बल्कि सम्पूर्ण गणित में लागू होती हैं।

🔵 युक्लिड के पाँच स्वयंसिद्ध (Euclid’s Five Postulates)
दो बिंदुओं को जोड़ने वाली एक ही सीधी रेखा खींची जा सकती है।
एक सीधी रेखा को दोनों दिशाओं में अनंत तक बढ़ाया जा सकता है।
किसी भी केंद्र और किसी भी त्रिज्या से वृत्त खींचा जा सकता है।
सभी समकोण (Right angles) एक-दूसरे के बराबर होते हैं।
यदि एक सीधी रेखा दो अन्य सीधी रेखाओं को इस प्रकार काटे कि एक ओर के अंतः कोणों का योग 180° से कम हो, तो वे रेखाएँ उस ओर मिलने के लिए बाध्य होंगी।
✏️ Note: पाँचवाँ स्वयंसिद्ध ही समानांतर रेखा स्वयंसिद्ध कहलाता है।

🟢 उदाहरण और अनुप्रयोग
सिक्के के किनारे पर खींचा गया वृत्त → तीसरे स्वयंसिद्ध का उदाहरण।
रेल की पटरियाँ → समानांतर रेखाओं की व्याख्या।
घर की दीवारें और फ़र्श → समतल सतह का उदाहरण।
💡 Concept: युक्लिड की ज्यामिति का आधार वास्तविक जीवन के अनुभव हैं।

🔴 युक्लिड की ज्यामिति और आधुनिक दृष्टिकोण
आज गणितज्ञ मानते हैं कि ज्यामिति केवल एक नहीं बल्कि कई प्रकार की हो सकती है (जैसे यूक्लिडीय और गैर-यूक्लिडीय ज्यामिति)। फिर भी, कक्षा 9 में हम केवल यूक्लिड की रचना को ही पढ़ते हैं।

🌿 प्रमेय (Theorems) का महत्व
युक्लिड ने दिखाया कि कैसे कुछ परिभाषाओं और स्वयंसिद्धों से अनेक प्रमेय सिद्ध किए जा सकते हैं।
उदाहरण:
त्रिभुज के कोणों का योग = 180°
विपरीत कोण बराबर होते हैं।

⚡ अध्याय का शैक्षिक महत्व
तर्क शक्ति का विकास
प्रमाण की विधि सीखना
गणित की संरचना को समझना
तार्किक सोच और विवेचना का अभ्यास

📌 Summary (~300 words)
युक्लिड और उसकी ज्यामिति
युक्लिड को “ज्यामिति का जनक” कहा जाता है।
उसकी पुस्तक एलिमेंट्स में गणित को व्यवस्थित रूप में प्रस्तुत किया गया।
परिभाषाएँ और धारणाएँ
बिंदु, रेखा, सतह आदि मूलभूत परिभाषाएँ दीं।
सामान्य धारणाएँ सार्वभौमिक गणितीय सत्य हैं।
स्वयंसिद्ध
पाँच मूलभूत स्वयंसिद्ध युक्लिड की ज्यामिति की रीढ़ हैं।
पाँचवाँ स्वयंसिद्ध (समानांतर रेखा स्वयंसिद्ध) सबसे महत्त्वपूर्ण है।
अनुप्रयोग
वृत्त, सीधी रेखा, समतल सतह और समकोण के दैनिक जीवन उदाहरण।
प्रमेय सिद्ध करने का आधार इन्हीं परिभाषाओं और स्वयंसिद्धों से लिया जाता है।
महत्व
विद्यार्थियों में तार्किकता और तर्क–वितर्क की क्षमता का विकास।
आधुनिक गणित और भौतिकी का आधार।
✔️ इस अध्याय का उद्देश्य केवल आकृतियाँ बनाना नहीं बल्कि गणितीय तर्क को समझना है।

📝 Quick Recap
🔵 युक्लिड को ज्यामिति का जनक कहा जाता है।
🟢 परिभाषाएँ: बिंदु, रेखा, सतह, समतल सतह।
🟡 सामान्य धारणाएँ: समानता और असमानता से जुड़े नियम।
🔴 पाँच स्वयंसिद्ध → विशेषकर समानांतर रेखा स्वयंसिद्ध।
🌿 तर्क और प्रमाण की विधि का अभ्यास।

————————————————————————————————————————————————————————————————————————————

पाठ्यपुस्तक के प्रश्न

प्रश्नावली 5.1

🔵 प्रश्न 1
निम्नलिखित कथनों में से कौन-से कथन सत्य हैं और कौन-से कथन असत्य हैं? अपने उत्तरों के लिए कारण दीजिए।
(i) एक बिंदु से होकर केवल एक ही रेखा खींची जा सकती है।
(ii) दो भिन्न बिंदुओं से होकर जाने वाली असंख्य रेखाएँ हैं।
(iii) एक सीधी रेखा दोनों ओर अनन्त रूप से बढ़ाई जा सकती है।
(iv) यदि दो वृत्त बराबर हैं, तो उनकी त्रिज्याएँ बराबर होती हैं।
(v) आकृति 5.9 में, यदि AB = PQ और PQ = XY है, तो AB = XY होगा।
🟢 उत्तर
🔵 (i) असत्य ➡️ क्योंकि एक बिंदु से होकर असंख्य रेखाएँ खींची जा सकती हैं।
🔵 (ii) असत्य ➡️ दो भिन्न बिंदुओं से होकर केवल एक ही रेखा गुजर सकती है।
🔵 (iii) सत्य ➡️ यह युक्लिड का स्वयंसिद्ध है कि एक सीधी रेखा दोनों ओर अनन्त रूप से बढ़ाई जा सकती है।
🔵 (iv) सत्य ➡️ यदि दो वृत्त बराबर हैं तो उनकी त्रिज्याएँ भी बराबर होंगी।
🔵 (v) सत्य ➡️ यदि AB = PQ और PQ = XY है, तो समता के गुण से AB = XY होगा।
✔️ अंतिम उत्तर: (iii), (iv), (v) सत्य; (i), (ii) असत्य।

🔵 प्रश्न 2
निम्नलिखित पदों में से प्रत्येक की परिभाषा दीजिए। क्या इनके लिए कुछ ऐसे पद हैं, जिन्हें परिभाषित करने की आवश्यकता नहीं? वे क्या हैं और आप इन्हें कैसे परिभाषित कर पाएँगे?
(i) समांतर रेखाएँ
(ii) लम्ब रेखाएँ
(iii) रेखाखंड
(iv) वृत्त की त्रिज्या
(v) वर्ग
🟢 उत्तर
🔵 (i) समांतर रेखाएँ ➡️ वे रेखाएँ जो एक ही समतल में हों और कभी प्रतिच्छेद न करें।
🔵 (ii) लम्ब रेखाएँ ➡️ दो रेखाएँ जो प्रतिच्छेद कर 90° कोण बनाएँ।
🔵 (iii) रेखाखंड ➡️ किसी रेखा का वह भाग जो दो निश्चित बिंदुओं के बीच स्थित हो।
🔵 (iv) वृत्त की त्रिज्या ➡️ वृत्त के केंद्र से वृत्त की परिधि पर स्थित किसी भी बिंदु तक की दूरी।
🔵 (v) वर्ग ➡️ वह चतुर्भुज जिसकी सभी भुजाएँ समान और सभी कोण समकोण हों।
✏️ Note: “बिंदु” और “रेखा” जैसे मूलभूत पद अपरिभाषित पद हैं; इन पर अन्य परिभाषाएँ आधारित हैं।

🔵 प्रश्न 3
नीचे दो हुई दो अभिधारणाओं पर विचार कीजिए:
(i) दो भिन्न बिंदु A और B दिए रहने पर, एक तीसरा बिंदु C ऐसा विधान है जो A और B के बीच विद्यमान होता है।
(ii) यहाँ कम से कम ऐसे तीन बिंदु विद्यमान हैं कि वे एक रेखा पर स्थित नहीं हैं।
क्या इन अभिधारणाओं में कोई अप्रयुक्त शब्द है? क्या ये अभिधारणाएँ आवश्यक हैं? क्या युक्लिड की अभिधारणाओं से प्राप्त होती हैं? स्पष्ट कीजिए।
🟢 उत्तर
🔵 (i) यहाँ “बीच” शब्द अप्रयुक्त है।
🔵 (ii) यहाँ “रेखा पर स्थित नहीं” अप्रयुक्त है।
🟢 ये अभिधारणाएँ आवश्यक हैं क्योंकि युक्लिड की परिभाषाओं से इनका प्रतिपादन नहीं होता।
✔️ अंतिम निष्कर्ष: ये युक्लिड की मौलिक अभिधारणाएँ मानी जाती हैं।

🔵 प्रश्न 4
यदि दो बिंदुओं A और B के बीच एक बिंदु C ऐसा है कि AC = BC है, तो सिद्ध कीजिए कि AC = 1/2 AB है।
🟢 उत्तर
🔵 दिया है: AC = BC
🔵 अतः AB = AC + CB
🔵 चूँकि AC = BC है ⇒ AB = AC + AC = 2AC
🔵 दोनों ओर 2 से भाग दीजिए: AC = AB/2
✔️ अंतिम उत्तर: AC = 1/2 AB

🔵 प्रश्न 5
प्रश्न 4 में, C रेखाखंड AB पर स्थित नहीं है। सिद्ध कीजिए कि एक रेखाखंड का एक और केवल एक मध्यबिंदु होता है।
🟢 उत्तर
🔵 मान लीजिए C, AB का मध्यबिंदु है।
🔵 यदि D भी AB का मध्यबिंदु हो, तो AC = CB तथा AD = DB होगा।
🔵 लेकिन एक ही रेखाखंड के दो अलग-अलग मध्यबिंदु नहीं हो सकते।
✔️ अंतिम उत्तर: एक रेखाखंड का केवल एक ही मध्यबिंदु होता है।

🔵 प्रश्न 6
आकृति 5.10 में, यदि AC = BD है, सिद्ध कीजिए कि AB = CD है।
🟢 उत्तर
🔵 दिया है: AC = BD
🔵 AB = AC + CB
🔵 CD = CB + BD
🔵 ⇒ AB = AC + CB = BD + CB = CD
✔️ अंतिम उत्तर: AB = CD

🔵 प्रश्न 7
युक्लिड की अभिधारणाओं की सूची में दिया हुआ पहला अभिधारणा 5 एक सर्वव्यापी सत्य क्यों माना जाता है? (ध्यान दीजिए कि यह अन्य पाँचवीं अभिधारणाओं से स्पष्ट नहीं है।)
🟢 उत्तर
🔵 अभिधारणा 5 कहती है: “यदि किसी रेखा को दो रेखाओं को काटने दो ऐसे कोण बनाएँ जो 2 समकोणों से छोटे हों, तो वे रेखाएँ अनन्त रूप से बढ़ाने पर प्रतिच्छेद करेंगी।”
🔵 यह सर्वव्यापी सत्य माना जाता है क्योंकि यह अन्य अभिधारणाओं से सिद्ध नहीं होता, केवल स्वीकार किया जाता है।
✔️ अंतिम उत्तर: अभिधारणा 5 स्वतःसिद्ध (axiom) रूप में मानी जाती है।

————————————————————————————————————————————————————————————————————————————

अन्य महत्वपूर्ण प्रश्न

🔵 खण्ड A (प्रत्येक 1 अंक, प्रश्न 1–6)
🔴 प्रश्न 1
🔵 युक्लिड की ज्यामिति किस देश में उत्पन्न हुई थी?
🟢 उत्तर
✔️ युक्लिड की ज्यामिति यूनान (ग्रीस) में उत्पन्न हुई थी।

🔴 प्रश्न 2
🔵 युक्लिड की प्रसिद्ध पुस्तक का नाम लिखिए।
🟢 उत्तर
✔️ युक्लिड की प्रसिद्ध पुस्तक का नाम एलीमेंट्स है।

🔴 प्रश्न 3
🔵 “एक बिन्दु केवल स्थिति को दर्शाता है, उसका कोई आकार नहीं होता” — यह किसकी परिभाषा है?
🟢 उत्तर
✔️ यह बिन्दु की परिभाषा है।

🔴 प्रश्न 4
🔵 युक्लिड ने कितनी परिभाषाएँ दी थीं?
🟢 उत्तर
✔️ युक्लिड ने कुल 23 परिभाषाएँ दी थीं।

🔴 प्रश्न 5
🔵 “यदि दो रेखाएँ एक ही बिन्दु से गुजरती हैं, तो वे सहसमतली होती हैं” — सत्य या असत्य?
🟢 उत्तर
✔️ यह सत्य है।

🔴 प्रश्न 6
🔵 युक्लिड के कितने स्वयंसिद्ध (Axioms) हैं?
🟢 उत्तर
✔️ युक्लिड के 7 स्वयंसिद्ध हैं।

🟢 खण्ड B (प्रत्येक 2 अंक, प्रश्न 7–12)
🔴 प्रश्न 7
🔵 “पूरे का भाग उसके पूरे से छोटा होता है” — किसका उदाहरण है?
🟢 उत्तर
✔️ यह युक्लिड का 5वाँ स्वयंसिद्ध है।

🔴 प्रश्न 8
🔵 यदि AB = CD और CD = EF, तो सिद्ध कीजिए कि AB = EF।
🟢 उत्तर
✳️ दिया गया: AB = CD, CD = EF
➤ समानता का संक्रामक गुण: यदि a = b और b = c, तो a = c
✔️ अतः AB = EF
➡️ अन्तिम उत्तर: AB = EF

🔴 प्रश्न 9
🔵 “सभी समकोण एक दूसरे के बराबर होते हैं” — यह किसका कथन है?
🟢 उत्तर
✔️ यह युक्लिड का 4था स्वयंसिद्ध है।

🔴 प्रश्न 10
🔵 सिद्ध कीजिए कि यदि दो परिमाण बराबर हों तो उनके बराबर में बराबर जोड़ने पर योग भी बराबर होगा।
🟢 उत्तर
✳️ दिया गया: a = b
➤ a + c = b + c
✔️ योगफल बराबर हैं।
➡️ अन्तिम उत्तर: सिद्ध।

🔴 प्रश्न 11
🔵 युक्लिड की परिभाषा के अनुसार रेखा क्या है?
🟢 उत्तर
✔️ रेखा वह है जिसकी केवल लम्बाई होती है, चौड़ाई नहीं होती।

🔴 प्रश्न 12
🔵 समतल की परिभाषा दीजिए।
🟢 उत्तर
✔️ समतल वह सतह है, जिस पर स्थित दो बिन्दुओं को मिलाने वाली कोई भी रेखा सम्पूर्णतः उसी सतह पर स्थित रहती है।

🟡 प्रश्न 13
🔵 युक्लिड के पहले स्वयंसिद्ध को लिखिए और एक उदाहरण दीजिए।
🟢 उत्तर
✳️ युक्लिड का पहला स्वयंसिद्ध है:
➤ यदि समान परिमाणों में समान जोड़ा जाए तो योग भी समान होंगे।
उदाहरण: यदि a = b है, तो a + c = b + c होगा।
➡️ अन्तिम उत्तर: पहला स्वयंसिद्ध और उदाहरण सिद्ध।

🟡 प्रश्न 14
🔵 “यदि समान परिमाणों में से समान घटाया जाए तो शेष परिमाण भी समान होंगे” — प्रमेय लिखिए और समझाइए।
🟢 उत्तर
✳️ दिया गया: a = b
➤ घटाया गया c
➤ तब a – c = b – c
✔️ घटाव के बाद भी शेष समान होंगे।
➡️ अन्तिम उत्तर: दूसरा स्वयंसिद्ध सिद्ध।

🟡 प्रश्न 15
🔵 बिन्दु और रेखा की परिभाषाएँ लिखिए।
🟢 उत्तर
✳️ बिन्दु: केवल स्थिति दर्शाता है, उसका कोई आकार नहीं होता।
✳️ रेखा: जिसकी केवल लम्बाई होती है, चौड़ाई नहीं।
➡️ अन्तिम उत्तर: बिन्दु और रेखा की परिभाषा स्पष्ट।

🟡 प्रश्न 16
🔵 सिद्ध कीजिए कि “यदि दो परिमाण किसी तीसरे परिमाण के बराबर हों, तो वे आपस में भी बराबर होंगे।”
🟢 उत्तर
✳️ दिया गया: a = c और b = c
➤ अतः a = b
✔️ यह समानता का गुण है।
➡️ अन्तिम उत्तर: प्रमेय सिद्ध।

🟡 प्रश्न 17
🔵 युक्लिड की ज्यामिति और आधुनिक ज्यामिति में मुख्य अन्तर स्पष्ट कीजिए।
🟢 उत्तर
✳️ युक्लिड की ज्यामिति में रेखा, समतल, बिन्दु आदि को व्यावहारिक रूप में परिभाषित किया गया है।
✳️ आधुनिक ज्यामिति में ये सभी केवल तार्किक मान्यताएँ (undefined terms) मानी जाती हैं।
➡️ अन्तिम उत्तर: अन्तर — परिभाषा की दृष्टि से।

🟡 प्रश्न 18
🔵 “सभी समकोण बराबर होते हैं” इस स्वयंसिद्ध का प्रयोग करके सिद्ध कीजिए कि 2 समकोण बराबर हैं।
🟢 उत्तर
✳️ समकोण की परिभाषा: 90° का कोण।
➤ ∠A = 90°, ∠B = 90°
➤ अतः ∠A = ∠B
➡️ अन्तिम उत्तर: सभी समकोण बराबर होते हैं।

🟡 प्रश्न 19 (आन्तरिक विकल्प)
🔵 युक्लिड के 5वें स्वयंसिद्ध को लिखिए।
🟢 उत्तर
✳️ 5वाँ स्वयंसिद्ध: यदि कोई रेखा दो रेखाओं को इस प्रकार काटे कि एक ओर के आन्तरिक कोणों का योग 180° से कम हो, तो वे रेखाएँ उस ओर मिलेंगी।
➡️ अन्तिम उत्तर: पाँचवाँ स्वयंसिद्ध।
OR
🔵 सहसमतली रेखाएँ क्या होती हैं?
🟢 उत्तर
✔️ वे सभी रेखाएँ जो एक ही समतल में स्थित होती हैं, सहसमतली कहलाती हैं।

🟡 प्रश्न 20
🔵 युक्लिड के किस स्वयंसिद्ध का प्रयोग करके यह कहा जाता है कि “बराबर परिमाणों का दोगुना बराबर होता है”?
🟢 उत्तर
✔️ यह तीसरे स्वयंसिद्ध का उदाहरण है।

🟡 प्रश्न 21
🔵 सिद्ध कीजिए कि यदि a = b हो तो 2a = 2b होगा।
🟢 उत्तर
✳️ दिया गया: a = b
➤ दोनों ओर ×2
➤ 2a = 2b
➡️ अन्तिम उत्तर: सिद्ध।

🟡 प्रश्न 22
🔵 युक्लिड की ज्यामिति के अध्ययन की आवश्यकता क्यों है?
🟢 उत्तर
✳️ यह ज्यामिति तार्किक सोच और प्रमाण की विधि सिखाती है।
✳️ गणितीय संरचनाओं की नींव इसी पर आधारित है।
✳️ वास्तविक जीवन की ज्यामितीय समस्याओं का समाधान इसी से निकलता है।
➡️ अन्तिम उत्तर: अध्ययन की आवश्यकता तार्किकता और उपयोगिता है।

🔴 प्रश्न 23
🔵 युक्लिड के तीसरे स्वयंसिद्ध को लिखिए और एक उदाहरण द्वारा समझाइए।
🟢 उत्तर
✳️ तीसरा स्वयंसिद्ध: यदि समान परिमाणों को समान गुणा किया जाए तो गुणनफल भी समान होंगे।
➤ यदि a = b हो, तो 2a = 2b होगा।
उदाहरण: यदि दो रेखाखण्ड PQ = RS हों, तो उनका दुगुना भी बराबर होगा।
➡️ अन्तिम उत्तर: तीसरा स्वयंसिद्ध तथा उदाहरण सिद्ध।

🔴 प्रश्न 24
🔵 युक्लिड के चौथे स्वयंसिद्ध को लिखिए और इसे कोणों पर लागू करके सिद्ध कीजिए।
🟢 उत्तर
✳️ चौथा स्वयंसिद्ध: सभी समकोण एक-दूसरे के बराबर होते हैं।
➤ समकोण = 90°
➤ यदि ∠A = 90° और ∠B = 90°
➤ तो ∠A = ∠B
➡️ अन्तिम उत्तर: सभी समकोण बराबर सिद्ध।

🔴 प्रश्न 25
🔵 युक्लिड के पाँचवें स्वयंसिद्ध को लिखिए और समझाइए कि यह समान्तर रेखाओं से कैसे सम्बंधित है।
🟢 उत्तर
✳️ पाँचवाँ स्वयंसिद्ध: यदि कोई रेखा दो अन्य रेखाओं को इस प्रकार काटे कि एक ओर के आन्तरिक कोणों का योग 180° से कम हो, तो वे रेखाएँ उस ओर अवश्य मिलेंगी।
🧠 यह स्वयंसिद्ध समान्तर रेखाओं की नींव है।
➡️ अन्तिम उत्तर: यह स्वयंसिद्ध समान्तर रेखाओं से सम्बन्धित है।

🔴 प्रश्न 26
🔵 “समान परिमाणों का समान गुणज समान होता है” — इस कथन को संख्यात्मक उदाहरण से सिद्ध कीजिए।
🟢 उत्तर
✳️ दिया गया: a = b
➤ गुणा करें 5 से → 5a = 5b
उदाहरण: यदि 2 = 2, तो 2×5 = 2×5 → 10 = 10
➡️ अन्तिम उत्तर: कथन सिद्ध।

🔴 प्रश्न 27 (आन्तरिक विकल्प)
🔵 युक्लिड की ज्यामिति में “रेखा” और “समतल” की परिभाषा लिखिए और उदाहरण दीजिए।
🟢 उत्तर
✳️ रेखा: केवल लम्बाई होती है, चौड़ाई नहीं।
✳️ समतल: एक ऐसा सतह जिस पर स्थित दो बिन्दुओं को मिलाने वाली रेखा भी उसी पर स्थित होती है।
उदाहरण: ब्लैकबोर्ड की सतह समतल का उदाहरण है।
OR
🔵 “यदि बराबर में बराबर जोड़े जाएँ तो योग बराबर होगा” — इसे संख्यात्मक उदाहरण से सिद्ध कीजिए।
🟢 उत्तर
✳️ दिया गया: 7 = 7
➤ दोनों ओर 3 जोड़ें → 7 + 3 = 7 + 3
➤ 10 = 10
➡️ अन्तिम उत्तर: कथन सिद्ध।

🔴 प्रश्न 28
🔵 युक्लिड की ज्यामिति की सीमाएँ स्पष्ट कीजिए।
🟢 उत्तर
✳️ यह केवल ठोस वस्तुओं के सामान्य आकारों पर आधारित है।
✳️ यह त्रिविमीय (3D) ज्यामिति की व्याख्या नहीं करती।
✳️ बिन्दु, रेखा, समतल आदि के लिए आधुनिक परिभाषा नहीं दी गयी।
➡️ अन्तिम उत्तर: युक्लिड की ज्यामिति सीमित है।

🔴 प्रश्न 29 (आन्तरिक विकल्प)
🔵 युक्लिड की ज्यामिति के योगदान को स्पष्ट कीजिए।
🟢 उत्तर
✳️ ज्यामिति को संगठित रूप दिया।
✳️ परिभाषाएँ, स्वयंसिद्ध और प्रमेयों की तार्किक श्रेणी प्रस्तुत की।
✳️ गणितीय प्रमाण की विधि का आधार रखा।
➡️ अन्तिम उत्तर: योगदान महान और आधारभूत।
OR
🔵 युक्लिड के 2 स्वयंसिद्ध लिखकर उदाहरण दीजिए।
🟢 उत्तर
✳️ पहला: बराबर में बराबर जोड़ने पर योग बराबर होता है → 3 = 3, 3+2=3+2=5
✳️ दूसरा: बराबर में बराबर घटाने पर शेष बराबर होता है → 6 = 6, 6–2=6–2=4
➡️ अन्तिम उत्तर: दोनों स्वयंसिद्ध सही उदाहरण सहित।

🔴 प्रश्न 30 (आन्तरिक विकल्प)
🔵 युक्लिड की ज्यामिति और आज की आधुनिक ज्यामिति में अन्तर स्पष्ट कीजिए।
🟢 उत्तर
✳️ युक्लिड: बिन्दु, रेखा, समतल को परिभाषित करता है।
✳️ आधुनिक: बिन्दु, रेखा, समतल को अपरिभाषित मानकर तार्किक स्वीकृतियाँ मानती है।
✳️ आधुनिक ज्यामिति में गैर-युक्लिडीय अवधारणाएँ भी सम्मिलित हैं।
➡️ अन्तिम उत्तर: अन्तर स्पष्ट।
OR
🔵 युक्लिड के पाँच प्रमुख योगदान सूचीबद्ध कीजिए।
🟢 उत्तर
✳️ 1. परिभाषाएँ दीं।
✳️ 2. 7 स्वयंसिद्ध और 5 मान्यताएँ प्रस्तुत कीं।
✳️ 3. प्रमेयों की तार्किक संरचना दी।
✳️ 4. गणितीय प्रमाण की विधि विकसित की।
✳️ 5. “एलीमेंट्स” पुस्तक द्वारा ज्ञान को व्यवस्थित किया।
➡️ अन्तिम उत्तर: पाँच योगदान सूचीबद्ध।

————————————————————————————————————————————————————————————————————————————

मानचित्र

————————————————————————————————————————————————————————————————————————————
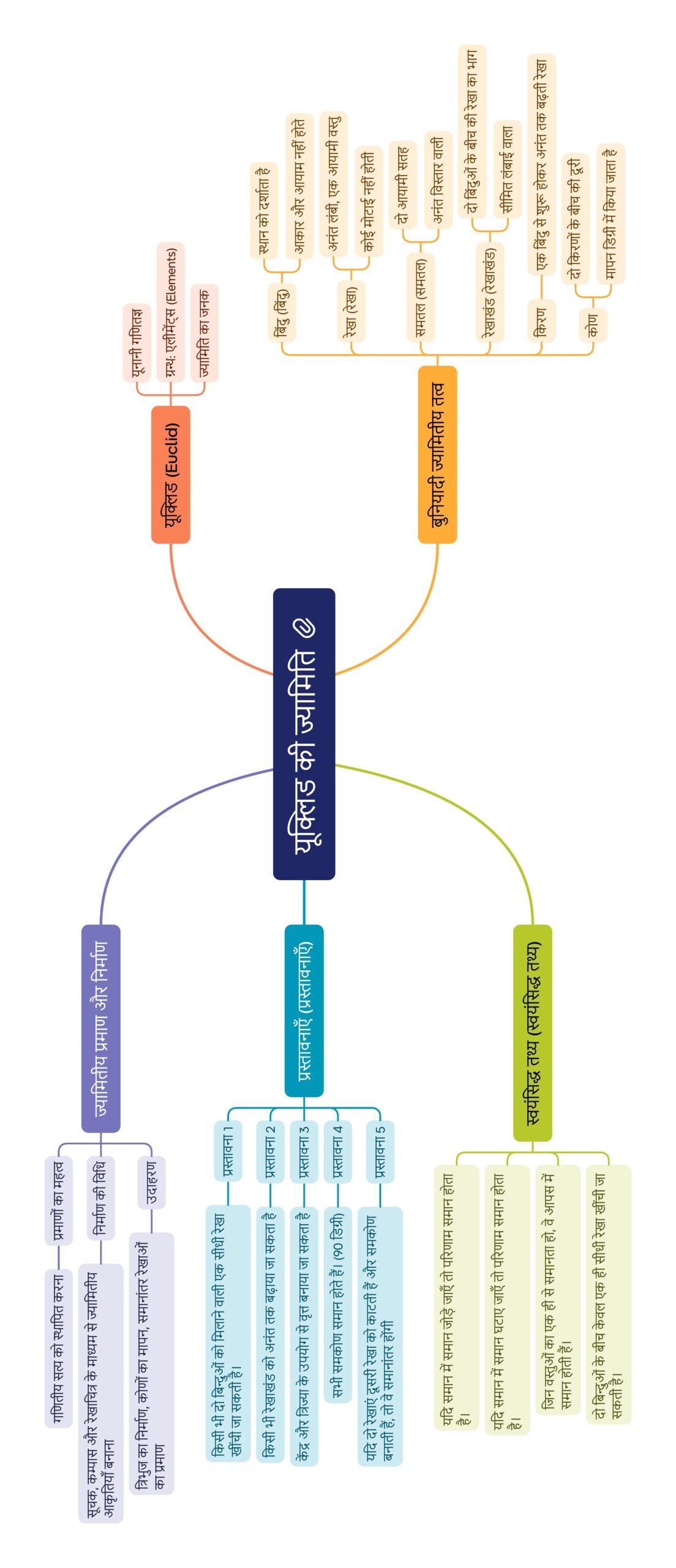